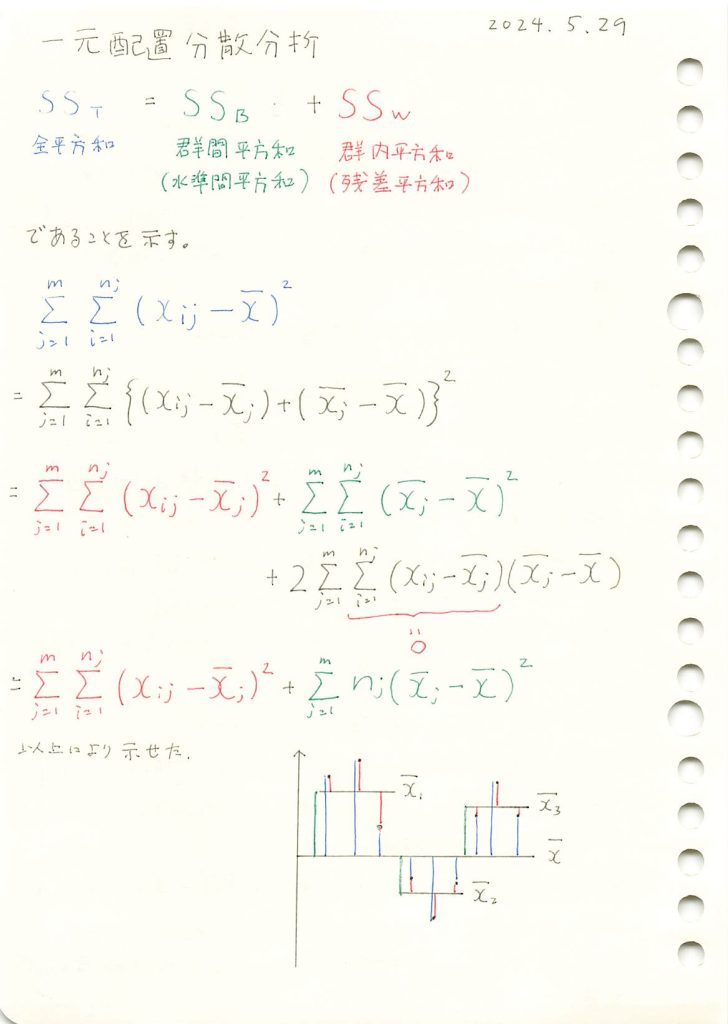
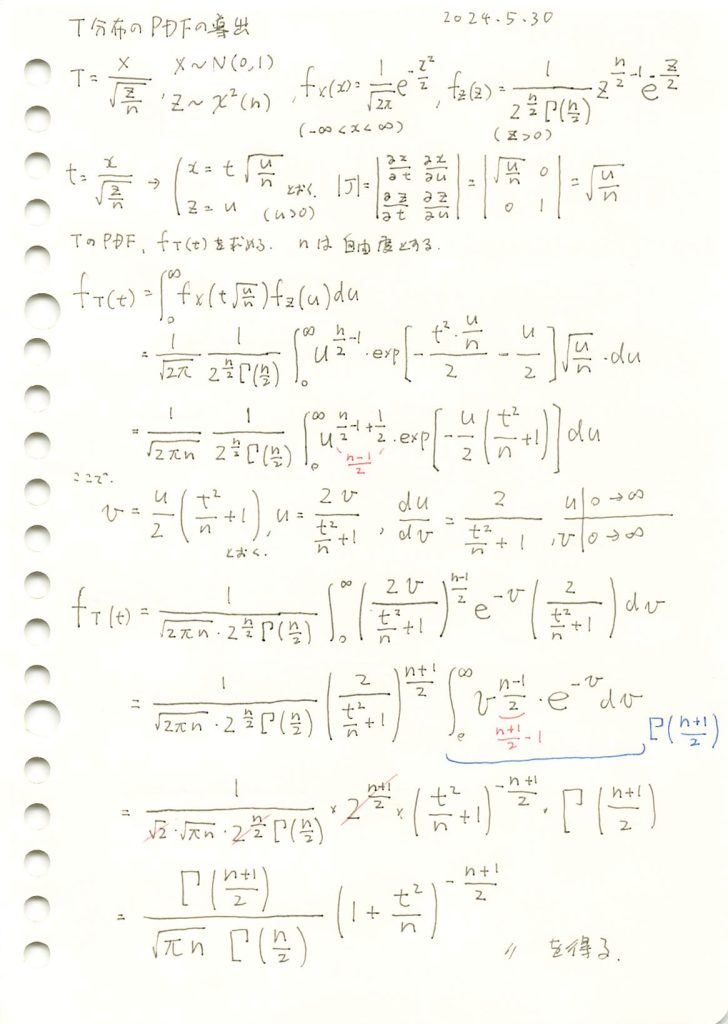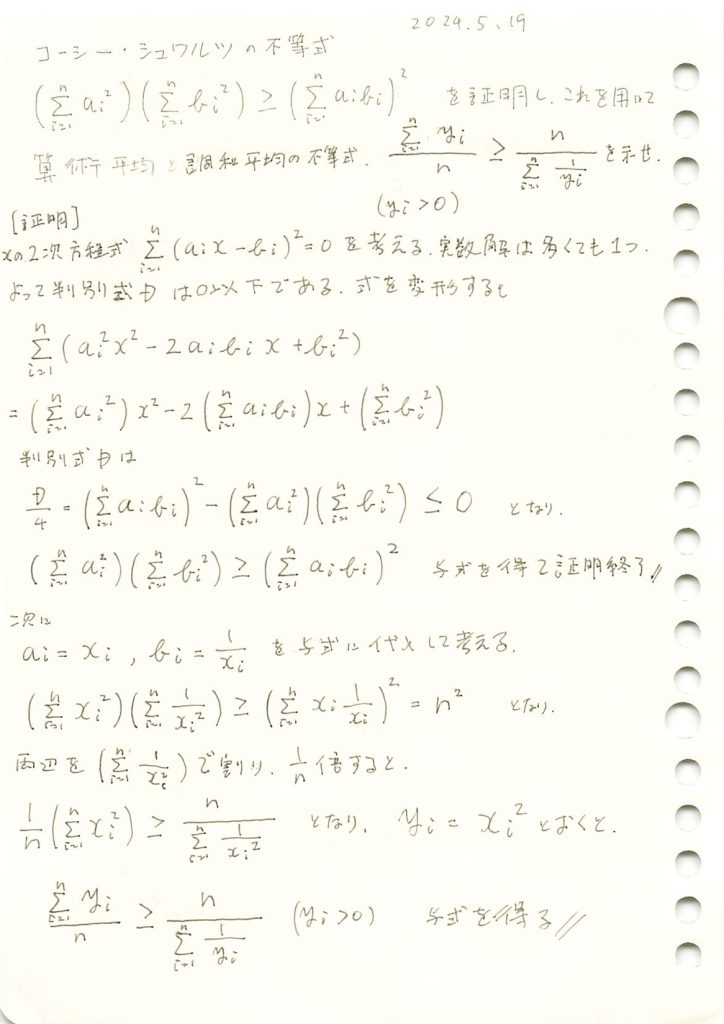ホーム » 統計検定1級 向け補助知識
「統計検定1級 向け補助知識」カテゴリーアーカイブ
混合ガウスモデルによる観測データの分布特性推定
概要:
本実験では、観測データが複数の異なる分布の混合によって生成されている可能性を考慮し、その分布特性を推定する手法を検証する。具体的には、2つの正規分布を混合したデータを生成し、EMアルゴリズムを用いてその混合ガウスモデルをフィッティングする。実験の結果、生成されたデータの背後にある各分布の平均、標準偏差、および混合割合を高精度に推定できることを確認した。本手法は、複雑な観測データに対する分布特性の解析やデータの要因分解に有効である。
2つの成分
import numpy as np
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
# 1. データ生成: 混合正規分布から乱数を生成
np.random.seed(0)
n_samples = 1000
# 2つの正規分布のパラメータ設定
mean1, std1 = 0, 1 # 正規分布1
mean2, std2 = 5, 1.5 # 正規分布2
weight1, weight2 = 0.4, 0.6 # 混合割合
# 2つの分布からデータ生成
data1 = np.random.normal(mean1, std1, int(weight1 * n_samples))
data2 = np.random.normal(mean2, std2, int(weight2 * n_samples))
# 混合データの作成
data = np.hstack([data1, data2])
np.random.shuffle(data)
# 2. 混合モデルの構築とフィッティング (EMアルゴリズムを使用)
gmm = GaussianMixture(n_components=2, random_state=0)
gmm.fit(data.reshape(-1, 1))
# 推定されたパラメータ
means = gmm.means_.flatten()
std_devs = np.sqrt(gmm.covariances_).flatten()
weights = gmm.weights_
print("推定された平均:", means)
print("推定された標準偏差:", std_devs)
print("推定された混合割合:", weights)
# 3. 結果のプロット
x = np.linspace(-3, 10, 1000)
pdf1 = weights[0] * (1 / (std_devs[0] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[0])**2 / (2 * std_devs[0]**2)))
pdf2 = weights[1] * (1 / (std_devs[1] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[1])**2 / (2 * std_devs[1]**2)))
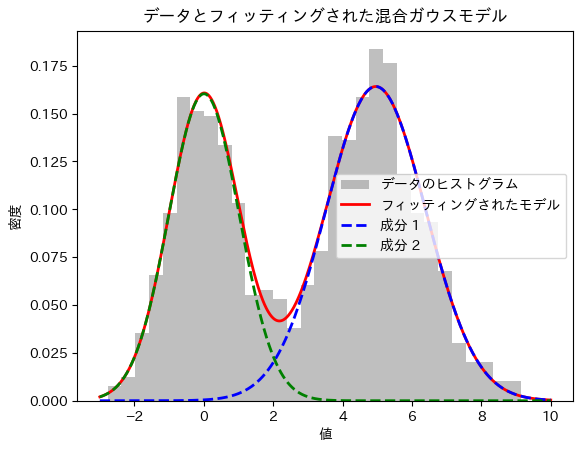
plt.hist(data, bins=30, density=True, alpha=0.5, color='gray', label='データのヒストグラム')
plt.plot(x, pdf1 + pdf2, 'r-', lw=2, label='フィッティングされたモデル')
plt.plot(x, pdf1, 'b--', lw=2, label='成分 1')
plt.plot(x, pdf2, 'g--', lw=2, label='成分 2')
plt.title('データとフィッティングされた混合ガウスモデル')
plt.xlabel('値')
plt.ylabel('密度')
plt.legend()
plt.show()
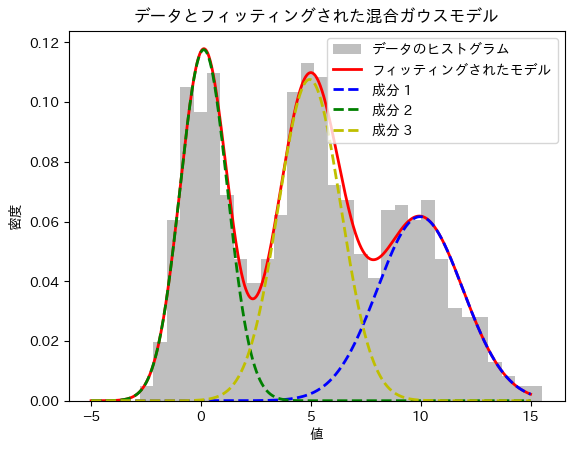
3つの成分
import numpy as np
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
# 1. データ生成: 混合正規分布から乱数を生成
np.random.seed(0)
n_samples = 1000
# 3つの正規分布のパラメータ設定
mean1, std1 = 0, 1 # 正規分布1
mean2, std2 = 5, 1.5 # 正規分布2
mean3, std3 = 10, 2 # 正規分布3
weight1, weight2, weight3 = 0.3, 0.4, 0.3 # 混合割合
# 3つの分布からデータ生成
data1 = np.random.normal(mean1, std1, int(weight1 * n_samples))
data2 = np.random.normal(mean2, std2, int(weight2 * n_samples))
data3 = np.random.normal(mean3, std3, int(weight3 * n_samples))
# 混合データの作成
data = np.hstack([data1, data2, data3])
np.random.shuffle(data)
# 2. 混合モデルの構築とフィッティング (EMアルゴリズムを使用)
gmm = GaussianMixture(n_components=3, random_state=0)
gmm.fit(data.reshape(-1, 1))
# 推定されたパラメータ
means = gmm.means_.flatten()
std_devs = np.sqrt(gmm.covariances_).flatten()
weights = gmm.weights_
print("推定された平均:", means)
print("推定された標準偏差:", std_devs)
print("推定された混合割合:", weights)
# 3. 結果のプロット
x = np.linspace(-5, 15, 1000)
pdf1 = weights[0] * (1 / (std_devs[0] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[0])**2 / (2 * std_devs[0]**2)))
pdf2 = weights[1] * (1 / (std_devs[1] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[1])**2 / (2 * std_devs[1]**2)))
pdf3 = weights[2] * (1 / (std_devs[2] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[2])**2 / (2 * std_devs[2]**2)))
plt.hist(data, bins=30, density=True, alpha=0.5, color='gray', label='データのヒストグラム')
plt.plot(x, pdf1 + pdf2 + pdf3, 'r-', lw=2, label='フィッティングされたモデル')
plt.plot(x, pdf1, 'b--', lw=2, label='成分 1')
plt.plot(x, pdf2, 'g--', lw=2, label='成分 2')
plt.plot(x, pdf3, 'y--', lw=2, label='成分 3')
plt.title('データとフィッティングされた混合ガウスモデル')
plt.xlabel('値')
plt.ylabel('密度')
plt.legend()
plt.show()