ホーム » 統計検定1級 2022年 統計数理 (ページ 3)
「統計検定1級 2022年 統計数理」カテゴリーアーカイブ
2022 Q1(3)
事象A,B,Cが独立とは限らない場合のP(A∩B∩C)の取り得る範囲を求めました。

コード
### 2022 Q1(3) 2024.7.27
import itertools
def generate_combinations(n, k):
base_list = [1] * k + [0] * (n - k)
all_combinations = set(itertools.permutations(base_list))
return list(all_combinations)
def calculate_intersection(A, B, C):
return np.mean(np.array(A) & np.array(B) & np.array(C))
def find_min_max_intersection(n, k):
all_combinations = generate_combinations(n, k)
min_intersection = 1.0
max_intersection = 0.0
for A in all_combinations:
for B in all_combinations:
for C in all_combinations:
intersection_ratio = calculate_intersection(A, B, C)
if intersection_ratio < min_intersection:
min_intersection = intersection_ratio
if intersection_ratio > max_intersection:
max_intersection = intersection_ratio
return min_intersection, max_intersection
# パラメータを設定
n = 8
k = 6
# 最小値と最大値を計算
min_intersection, max_intersection = find_min_max_intersection(n, k)
min_intersection, max_intersection
(0.25, 0.75)アルゴリズム
- 組み合わせの生成
- 配列の長さ
nを8、1の数kを6と設定する。 - 配列
11111100を作成し、itertools.permutationsを使ってすべての並べ替えを生成する。
- 配列の長さ
- 交差部分の確率計算
- すべての組み合わせに対して、配列
A,B,Cを選ぶ。 - 例えば、
A = 11111100,B = 11011110,C = 11101110の場合、交差部分A & B & Cは11001100となる。これにより、確率は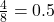 となる。
となる。
- すべての組み合わせに対して、配列
- 最小値と最大値の取得
- すべての組み合わせに対して計算した確率を比較し、最小値と最大値を更新する。
- 最終的に、最小値と最大値を返す。
2022 Q1(1)(2)
事象A,Bが独立なときと、そうとは限らない場合の確率の取り得る範囲の計算をしました。

(1)コード
### 2022 Q1(1) 2024.7.26
import numpy as np
# シミュレーションの回数
num_simulations = 1000000
# 与えられた確率
prob = 3/4
# 事象 A, B, C をシミュレーション
A = np.random.rand(num_simulations) < prob
B = np.random.rand(num_simulations) < prob
C = np.random.rand(num_simulations) < prob
# 交差確率の計算
P_A_and_B = np.mean(A & B)
P_A_and_B_and_C = np.mean(A & B & C)
P_A_and_B, P_A_and_B_and_C
(0.56311, 0.422594)#検算
9/16,27/64(0.5625, 0.421875)(2)コード
### 2022 Q1(2) 2024.7.26
import numpy as np
def simulate_overlap_with_fixed_true(correlation):
P_A = 3/4
P_B = 3/4
num_elements = 1000
num_true_A = int(P_A * num_elements)
num_true_B = int(P_B * num_elements)
# A と B の配列を生成し、3/4がtrueになるように設定
A = np.zeros(num_elements, dtype=bool)
A[:num_true_A] = True
np.random.shuffle(A)
B = np.zeros(num_elements, dtype=bool)
B[:num_true_B] = True
np.random.shuffle(B)
if correlation == 'positive':
# 正の相関を持たせるために、スワップを行う
A1_B0_indices = np.where(A & ~B)[0]
A0_B1_indices = np.where(~A & B)[0]
min_len = min(len(A1_B0_indices), len(A0_B1_indices))
for i in range(min_len):
B[A1_B0_indices[i]], B[A0_B1_indices[i]] = B[A0_B1_indices[i]], B[A1_B0_indices[i]]
elif correlation == 'negative':
# 負の相関を持たせるために、スワップを行う
A1_B1_indices = np.where(A & B)[0]
A0_B0_indices = np.where(~A & ~B)[0]
min_len = min(len(A1_B1_indices), len(A0_B0_indices))
for i in range(min_len):
B[A1_B1_indices[i]], B[A0_B0_indices[i]] = B[A0_B0_indices[i]], B[A1_B1_indices[i]]
else:
raise ValueError("Invalid correlation type")
# 重なりの割合を計算
overlap_ratio = np.mean(A & B)
return overlap_ratio
# 正の相関の場合
overlap_positive = simulate_overlap_with_fixed_true('positive')
# 負の相関の場合
overlap_negative = simulate_overlap_with_fixed_true('negative')
overlap_positive, overlap_negative(0.75, 0.5)アルゴリズム
- パラメータの設定
- 事象 (A) の発生確率 (P_A) を設定する(ここでは 3/4)。
- 事象 (B) の発生確率 (P_B) を設定する(ここでは 3/4)。
- 配列の要素数 (num_elements) を設定する(ここでは 1000)。
- シミュレーションの回数 (num_simulations) を設定する(ここでは 1000)。
- 配列の初期化
- 配列 (A) と (B) をそれぞれ3/4がtrueになるように生成する。
- 配列 (A) に対して、最初の (num_true_A) 個を true に設定し、残りを false に設定する。その後、配列をシャッフルする。
- 配列 (B) に対しても同様の処理を行う。
- 相関の付与
- 正の相関を持たせる場合:
- 配列 (A) と (B) の要素をスワップして、 (A = 1, B = 0) と (A = 0, B = 1) の組を見つけたら、これらをスワップして値を揃える。
- 負の相関を持たせる場合:
- 配列 (A) と (B) の要素をスワップして、 (A = 1, B = 1) と (A = 0, B = 0) の組を見つけたら、これらをスワップして値が揃わないようにする。
- 重なりの割合の計算
- 配列 (A) と (B) の共通部分(重なり部分)を計算し、その割合を求める。
- 結果の記録
- 重なりの割合をリストに記録する。
- シミュレーション回数分、上記のステップを繰り返す。
- 最小値と最大値の取得
- 重なりの割合のリストから、最小値と最大値を取得する。