ホーム » 統計検定1級 2019年 統計数理 (ページ 3)
「統計検定1級 2019年 統計数理」カテゴリーアーカイブ
カテゴリー
- F分布 (3)
- t分布 (1)
- カイ二乗分布 (11)
- ガンマ分布 (12)
- コーシー分布 (5)
- コードあり (175)
- コードあり2 (2)
- コクランの定理 (3)
- チェビシェフの不等式 (1)
- フィッシャー情報量 (1)
- ベイズ統計 (4)
- ベルヌーイ試行 (1)
- ポアソン分布 (15)
- マルコフ性 (3)
- モーメント (1)
- モーメント母関数 (4)
- モンテカルロ法 (4)
- ラプラス分布 (5)
- 一様分布 (19)
- 一致推定量 (1)
- 不偏推定量 (8)
- 二項分布 (16)
- 仮説検定 (6)
- 信頼区間推定 (4)
- 分布 (0)
- 分散分析 (2)
- 十分統計量 (2)
- 多項分布 (6)
- 尖度 (2)
- 尤度 (1)
- 尤度比 (3)
- 平均二乗誤差MSE (12)
- 復習3周目 (183)
- 復習4周目 (177)
- 復習5周目 (172)
- 指数分布 (13)
- 損失関数 (1)
- 最尤推定 (10)
- 最強力検定 (2)
- 検出力 (4)
- 正規分布 (5)
- 歪度 (2)
- 混合分布 (1)
- 確率母関数 (3)
- 統計検定1級 2014年 統計数理 (22)
- 統計検定1級 2015年 統計数理 (26)
- 統計検定1級 2016年 統計数理 (21)
- 統計検定1級 2017年 統計数理 (18)
- 統計検定1級 2018年 統計数理 (26)
- 統計検定1級 2019年 統計数理 (23)
- 統計検定1級 2021年 統計数理 (21)
- 統計検定1級 2022年 統計数理 (22)
- 統計検定1級 向け補助知識 (21)
- 線形モデル (10)
- 負の二項分布 (3)
- 超幾何分布 (11)
- 過誤確率 (1)
- 適合度 (3)
- 順序統計量 (5)
投稿一覧
2014 Q1(1)
2014 Q1(2)
2014 Q1(3)
2014 Q2(1)
2014 Q2(2)
2014 Q2(3)
2014 Q2(4)
2014 Q2(5)
2014 Q3(1)
2014 Q3(2)
2014 Q3(2)
2014 Q4(1)-1
2014 Q4(1)-2
2014 Q4(2)
2014 Q4(3)
2014 Q4(4)
2014 Q4(4)
2014 Q4(5)
2014 Q5(1)
2014 Q5(2)
2014 Q5(3)
2014 Q5(4)
2015 Q1(1)
2015 Q1(2)
2015 Q1(3)
2015 Q1(4)
2015 Q1(5)
2015 Q2(1)
2015 Q2(2)
2015 Q2(3)
2015 Q2(4)
2015 Q2(5)
2015 Q3(1)
2015 Q3(2)
2015 Q3(3)
2015 Q3(4)
2015 Q3(4)
2015 Q4(1)
2015 Q4(2)
2015 Q4(3)
2015 Q4(4)
2015 Q4(5)
2015 Q5(1)
2015 Q5(2)
2015 Q5(3)
2015 Q5(4)
2015 Q5(5)
2015 Q5(6)
2016 Q1(1)
2016 Q1(2)
2016 Q1(3)
2016 Q1(4)
2016 Q2(1)
2016 Q2(2)
2016 Q2(3)
2016 Q2(4)
2016 Q2(4)
2016 Q3(1)
2016 Q3(2)
2016 Q3(3)
2016 Q3(3)
2016 Q4(1)
2016 Q4(2)
2016 Q4(3)
2016 Q4(4)
2016 Q5(1)
2016 Q5(2)
2016 Q5(3)
2016 Q5(4)(5)
2017 Q1(1)
2017 Q1(2)
2017 Q1(3)
2017 Q1(4)
2017 Q1(5)
2017 Q2(1)
2017 Q2(2)
2017 Q2(3)
2017 Q2(4)
2017 Q3(1)
2017 Q3(2)
2017 Q3(3)
2017 Q3(4)
2017 Q4(1)(2)(3)
2017 Q4(4)
2017 Q5(1)
2017 Q5(2)
2017 Q5(3)
2018 Q1(1)
2018 Q1(2)-1
2018 Q1(2)-2
2018 Q1(2)-3
2018 Q1(3)
2018 Q1(4)-1
2018 Q1(4)-2
2018 Q2(1)-1
2018 Q2(1)-2
2018 Q2(2)
2018 Q2(3)
2018 Q2(4)
2018 Q2(5)-1
2018 Q2(5)-2
2018 Q3(1)
2018 Q3(2)
2018 Q3(3)
2018 Q3(4)
2018 Q3(5)
2018 Q4(1)
2018 Q4(2)-1
2018 Q4(2)-2
2018 Q4(3)
2018 Q5(1)
2018 Q5(2)
2018 Q5(3)
2019 Q1(1)
2019 Q1(2)
2019 Q1(4)
2019 Q2(1)
2019 Q2(2)
2019 Q2(3)
2019 Q2(4)
2019 Q3(1)
2019 Q3(2)
2019 Q3(3)
2019 Q3(4)
2019 Q3(5)
2019 Q3(6)
2019 Q4(1)
2019 Q4(2)
2019 Q4(3)
2019 Q4(4)
2019 Q5(1)-1
2019 Q5(1)-2
2019 Q5(2)
2019 Q5(3)
2019 Q5(4)
2021 Q1(1)(2)
2021 Q1(3)
2021 Q1(4)
2021 Q2(1)
2021 Q2(2)
2021 Q2(3)
2021 Q2(4)
2021 Q3(1)
2021 Q3(2)[2-1]
2021 Q3(2)[2-2]
2021 Q3(2)[2-3]
2021 Q3(3)
2021 Q3(4)
2021 Q4(1)(2)
2021 Q4(3)
2021 Q4(4)
2021 Q4(5)
2021 Q5(1)
2021 Q5(2)
2021 Q5(3)
2021 Q5(4)
2022 Q1(1)(2)
2022 Q1(3)
2022 Q1(4)
2022 Q2(1)
2022 Q2(2)(3)
2022 Q2(4)
2022 Q2(5)
2022 Q3(1)
2022 Q3(2)
2022 Q3(3)
2022 Q3(4)
2022 Q3(5)
2022 Q4(1)
2022 Q4(2)
2022 Q4(3)
2022 Q4(4)
2022 Q4(5)
2022 Q5(1)
2022 Q5(2)
2022 Q5(3)
2022 Q5(4)
2022 Q5(5)
2変数の和と和の共分散
F分布の確率密度関数の導出
T分布の確率密度関数の導出
コーシー・シュワルツの不等式の証明
ラグランジュ関数
一元配置分散分析の全平方和
二項分布と超幾何分布
多項定理
尖度の計算でマイナス3がついている
条件Z付きの条件付き分散の公式
条件Z付きの条件付き期待値の公式
条件付き分散の公式
条件付き分散の公式の導出
条件付き期待値の公式
条件付き期待値の公式の導出
標準正規分布に従うXとYの和
標準正規分布のモーメント母関数
欠損のメカニズム
混合ガウスモデルによる観測データの分布特性推定
独立でない確率変数の積の期待値について考えました。
線形変換された確率変数のモーメント母関数
非心カイ二乗分布
2019 Q1(3)
投稿日:2024年2月21日 最終更新日:2025年5月25日
確率母関数の不等式を証明する問題をやりました。

コード
不等式![]() を可視化して確認しました。ここでは二項分布で試しています。
を可視化して確認しました。ここでは二項分布で試しています。
# 2019 Q1(3) 2024.9.11
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 10 # 二項分布の試行回数
p = 0.5 # 二項分布の成功確率
t_values = [0.001, 0.2, 0.4, 0.6, 0.8, 1] # t の値のリスト
sample_size = 10000 # サンプル数
r_values = np.arange(0, n+1, 1) # r の範囲を設定
# 確率母関数 G_X(t) の定義
def G_X(t, n, p):
return (p * t + (1 - p))**n
# 1. 二項分布から乱数を生成
samples = np.random.binomial(n, p, sample_size)
# 2. r に対する P(X <= r) の推定(左辺)
P_X_leq_r_values = [np.sum(samples <= r) / sample_size for r in r_values]
# サブプロットの作成
fig, axes = plt.subplots(2, 3, figsize=(15, 8)) # 2行3列のサブプロットを作成
# 3. 各 t に対するグラフを描画
for i, t in enumerate(t_values):
row = i // 3 # 行番号
col = i % 3 # 列番号
# 右辺 t^{-r} G_X(t) の計算
G_X_value = G_X(t, n, p) # 確率母関数の t 固定
right_hand_side_values = [G_X_value if t == 1 else t**(-r) * G_X_value for r in r_values] # t = 1 の場合はべき乗を回避
# グラフの描画
ax = axes[row, col]
ax.plot(r_values, P_X_leq_r_values, label="P(X <= r) (左辺)", color="blue", linestyle="--")
ax.plot(r_values, right_hand_side_values, label="t^(-r) G_X(t) (右辺)", color="red")
ax.set_title(f"t = {t}")
ax.set_xlabel("r")
ax.set_ylabel("値 (対数スケール)")
ax.set_yscale('log') # 縦軸を対数スケールに設定
ax.legend()
ax.grid(True, which="both", ls="--")
# サブプロット間のレイアウト調整
plt.tight_layout()
plt.show()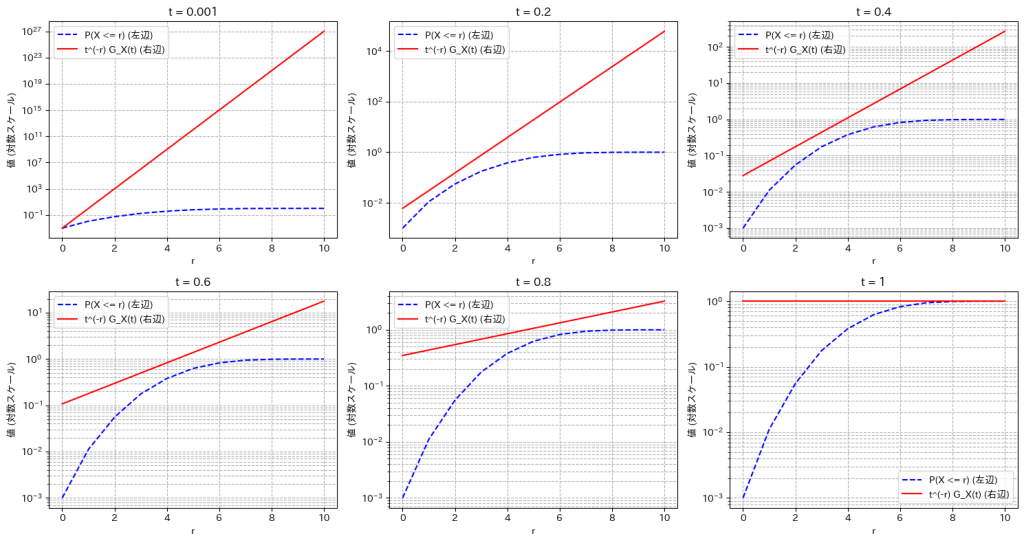
不等式![]() が成り立っていることが確認できました
が成り立っていることが確認できました
2019 Q1(2)
投稿日:2024年2月20日 最終更新日:2025年5月25日
二項分布の確率母関数を求め、期待値と分散を算出しました。
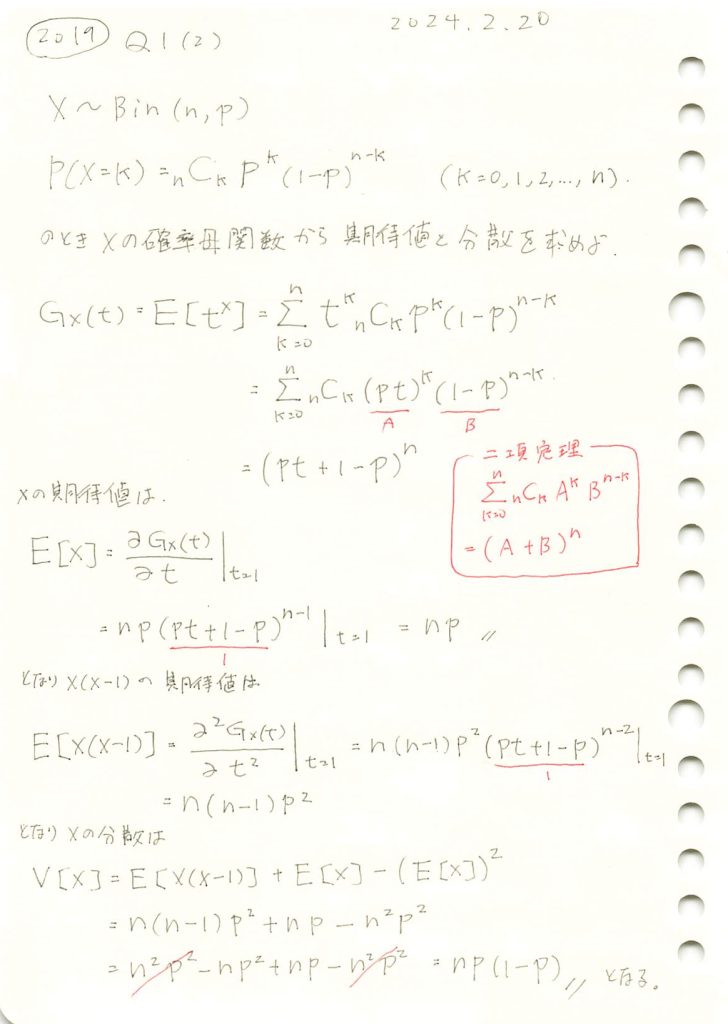
コード
非負の離散型観測データから確率母関数を構築し、これの微分と2階微分から期待値と分散を求めます。ここでは、観測データとして二項分布の乱数を用いて、その理論的な母関数と期待値と分散の比較を行います。
# 2019 Q1(2) 2024.9.10
import numpy as np
import matplotlib.pyplot as plt
from scipy.misc import derivative
# パラメータ設定
n = 10 # 試行回数
p = 0.5 # 成功確率
sample_size = 10000 # サンプル数
# 1. 二項分布に従う乱数データを生成
samples = np.random.binomial(n, p, sample_size)
# 2. P(X=k) の推定(サンプル度数から確率質量関数の推定)
max_k = np.max(samples)
pmf_estimate = np.zeros(max_k + 1)
for k in range(max_k + 1):
pmf_estimate[k] = np.sum(samples == k) / sample_size
# 3. G_X(t) の推定
def G_X(t):
return np.sum([pmf_estimate[k] * t**k for k in range(max_k + 1)])
# 4. 理論的な G_X(t) (二項分布の確率母関数)
def G_X_theoretical(t, n, p):
return (p * t + (1 - p))**n
# 5. G_X(t) のプロット
t_values = np.linspace(0, 1, 100)
G_X_values = [G_X(t) for t in t_values]
G_X_theoretical_values = [G_X_theoretical(t, n, p) for t in t_values]
plt.plot(t_values, G_X_values, label="推定された G_X(t)", color="blue")
plt.plot(t_values, G_X_theoretical_values, label="理論的な G_X(t)", linestyle='--', color="red")
plt.title("推定された確率母関数と理論的な G_X(t) の比較")
plt.xlabel("t")
plt.ylabel("G_X(t)")
plt.legend()
plt.show()
# 6. G_X(t) の微分と2階微分
def G_X_diff_1(t):
return derivative(G_X, t, dx=1e-6)
def G_X_diff_2(t):
return derivative(G_X_diff_1, t, dx=1e-6)
# 7. t = 1 における期待値と分散の推定
E_X_estimated = G_X_diff_1(1) # 期待値
Var_X_estimated = G_X_diff_2(1) + E_X_estimated - E_X_estimated**2 # 分散
# 結果の出力
print(f"推定された期待値 E[X]: {E_X_estimated}")
print(f"推定された分散 Var(X): {Var_X_estimated}")
# 真の期待値と分散を計算
E_X_true = n * p
Var_X_true = n * p * (1 - p)
# 真の期待値と分散を出力
print(f"真の期待値 E[X]: {E_X_true}")
print(f"真の分散 Var(X): {Var_X_true}")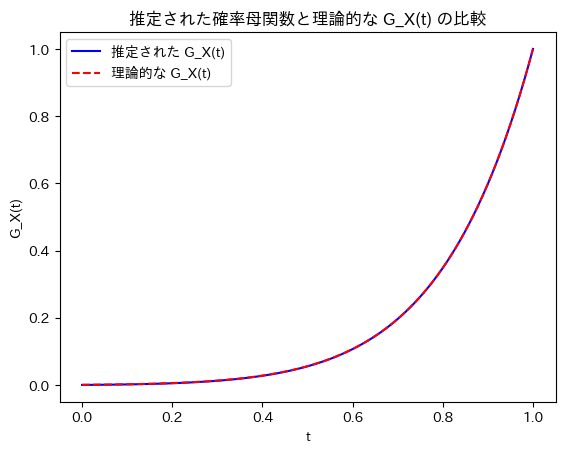
推定された期待値 E[X]: 4.9988999998862305
推定された分散 Var(X): 2.4964947096596752
真の期待値 E[X]: 5.0
真の分散 Var(X): 2.5観測値から推定された確率母関数は理論的な二項分布の確率母関数と一致しました。また、推定された確率母関数から計算された期待値と分散も、真の値に非常に近い結果となりました。
次に、二項分布の確率母関数![]() 、その1階微分
、その1階微分 ![]() 、および2階微分
、および2階微分 ![]() を視覚的に比較してみます。
を視覚的に比較してみます。
# 2019 Q1(2) 2024.9.10
import numpy as np
import matplotlib.pyplot as plt
from scipy.misc import derivative
# パラメータ設定
n = 10 # 試行回数
p = 0.5 # 成功確率
# 確率母関数 G_X(t)
def G_X(t, n, p):
return (p * t + (1 - p))**n
# 1階微分 G'_X(t)
def G_X_diff_1(t, n, p):
return derivative(lambda t: G_X(t, n, p), t, dx=1e-6)
# 2階微分 G''_X(t)
def G_X_diff_2(t, n, p):
return derivative(lambda t: G_X_diff_1(t, n, p), t, dx=1e-6)
# t の範囲を定義
t_values = np.linspace(0, 1, 100)
# G_X(t), G'_X(t), G''_X(t) の値を計算
G_X_values = [G_X(t, n, p) for t in t_values]
G_X_diff_1_values = [G_X_diff_1(t, n, p) for t in t_values]
G_X_diff_2_values = [G_X_diff_2(t, n, p) for t in t_values]
# グラフの描画
plt.plot(t_values, G_X_values, label="G_X(t) (確率母関数)", color="blue")
plt.plot(t_values, G_X_diff_1_values, label="G'_X(t) (1階微分)", color="green")
plt.plot(t_values, G_X_diff_2_values, label="G''_X(t) (2階微分)", color="red")
plt.title(f"G_X(t), G'_X(t), G''_X(t) の比較 (n={n}, p={p})")
plt.xlabel("t")
plt.ylabel("値")
plt.legend()
plt.grid(True)
plt.show()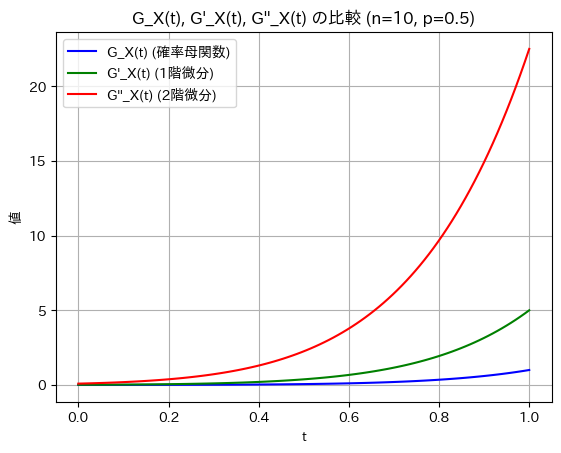
微分を重ねるごとにt=1付近での傾きが急になり大きな値を取っています。期待値や分散などの高次統計量に関連しているため、その値が大きくなっていると思います。
2019 Q1(1)
投稿日:2024年2月19日 最終更新日:2025年5月25日
非負の整数を取る離散確率変数の確率母関数の定義式から期待値と分散を求める式を導出しました。

コード
非負の離散型観測データから確率母関数を構築し、これの微分と2階微分から期待値と分散を求めます。ここでは、観測データとしてポアソン分布の乱数を用いて、その理論的な母関数と期待値と分散の比較を行います。
# 2019 Q1(1) 2024.9.9
import numpy as np
import matplotlib.pyplot as plt
from scipy.misc import derivative
# パラメータ設定
lambda_val = 3 # ポアソン分布のパラメータ λ
sample_size = 10000 # サンプル数
# 1. ポアソン分布に従う乱数データを生成
samples = np.random.poisson(lambda_val, sample_size)
# 2. P(X=k) の推定(サンプル度数から確率質量関数の推定)
max_k = np.max(samples)
pmf_estimate = np.zeros(max_k + 1)
for k in range(max_k + 1):
pmf_estimate[k] = np.sum(samples == k) / sample_size
# 3. G_X(t) の推定
def G_X(t):
return np.sum([pmf_estimate[k] * t**k for k in range(max_k + 1)])
# 4. 理論的な G_X(t) (ポアソン分布の確率母関数)
def G_X_theoretical(t, lam):
return np.exp(lam * (t - 1))
# 5. G_X(t) のプロット
t_values = np.linspace(0, 1, 100)
G_X_values = [G_X(t) for t in t_values]
G_X_theoretical_values = [G_X_theoretical(t, lambda_val) for t in t_values]
plt.plot(t_values, G_X_values, label="推定された G_X(t)", color="blue")
plt.plot(t_values, G_X_theoretical_values, label="理論的な G_X(t)", linestyle='--', color="red")
plt.title("推定された確率母関数と理論的な G_X(t) の比較")
plt.xlabel("t")
plt.ylabel("G_X(t)")
plt.legend()
plt.show()
# 6. G_X(t) の微分と2階微分
def G_X_diff_1(t):
return derivative(G_X, t, dx=1e-6)
def G_X_diff_2(t):
return derivative(G_X_diff_1, t, dx=1e-6)
# 7. t = 1 における期待値と分散の推定
E_X_estimated = G_X_diff_1(1) # 期待値
Var_X_estimated = G_X_diff_2(1) + E_X_estimated - E_X_estimated**2 # 分散
# 結果の出力
print(f"推定された期待値 E[X]: {E_X_estimated}")
print(f"推定された分散 Var(X): {Var_X_estimated}")
# 真の λ と比較
print(f"真の期待値 E[X]: {lambda_val}")
print(f"真の分散 Var(X): {lambda_val}")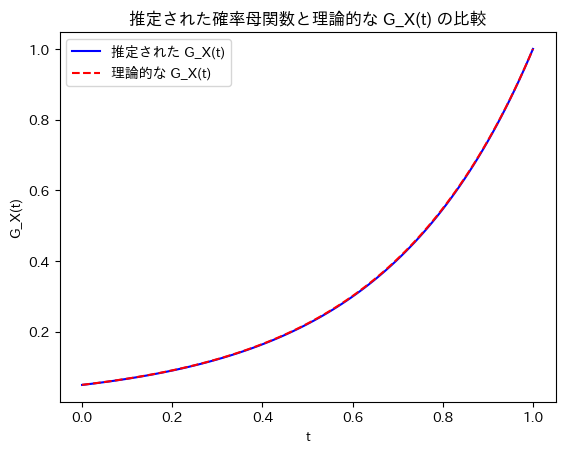
推定された期待値 E[X]: 3.0239000000098493
推定された分散 Var(X): 3.0824841743413582
真の期待値 E[X]: 3
真の分散 Var(X): 3観測値から推定された確率母関数は理論的なポアソン分布の確率母関数と一致しました。また、推定された確率母関数から計算された期待値と分散も、真の値に非常に近い結果となりました。