ホーム » 統計検定1級 2019年 統計数理
「統計検定1級 2019年 統計数理」カテゴリーアーカイブ
2019 Q5(4)
前問の式をグラフに描画しました。
コード
グラフをプロットします。
# 2019 Q5(4) 2024.9.30
import numpy as np
import matplotlib.pyplot as plt
# μハット(事後分布のモード)を計算する関数
def mu_hat(y_mean, lambd, xi, n):
if y_mean > xi:
return max(y_mean - lambd / n, xi)
elif y_mean < xi:
return min(y_mean + lambd / n, xi)
else:
return xi
# パラメータ設定
xi = 0 # ラプラス分布の中央値
lambd = 1 # スケールパラメータ
n_samples = 5 # サンプル数
# ȳ(観測データの平均)の範囲を設定 (-1 から 1)
y_mean_values = np.linspace(-1, 1, 500)
# μハットの値を計算
mu_hat_values = [mu_hat(y_mean, lambd, xi, n_samples) for y_mean in y_mean_values]
# グラフをプロット
plt.plot(y_mean_values, mu_hat_values, label='μハット (事後分布のモード)', color='red')
plt.plot(y_mean_values, y_mean_values, label='ȳ (標本平均)', color='blue', linestyle='--')
plt.title(f'標本平均 ȳ と 推定値 μハットの比較 (ξ = {xi}, λ = {lambd}, n = {n_samples})')
plt.xlabel('ȳ (標本平均)')
plt.ylabel('μハット (推定値)')
plt.legend()
plt.grid(True)
plt.show()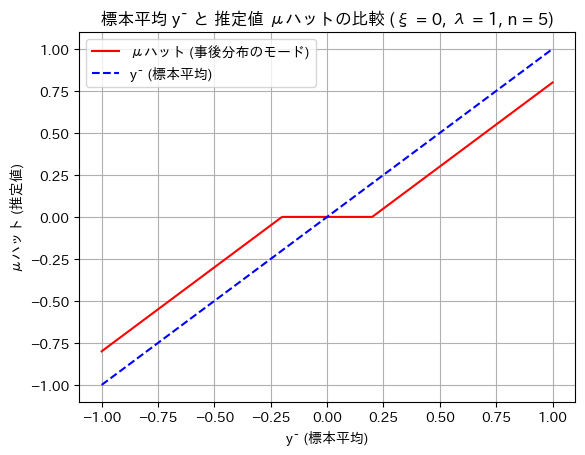
![]() がξに近いとき、
がξに近いとき、![]() はξになるという特徴があるようです。
はξになるという特徴があるようです。
2019 Q5(3)
前問の事後確率密度関数の最大値を取る期待値μを求めました。

追記
■2025/2/4 ![]() や
や![]() の導き方
の導き方
![]()
を変形し
![]()
となる。
ここで、![]() と
と![]() の符号を考えると、同符号のとき、第一項は異符号のときと比べて大きくなる。なぜなら
の符号を考えると、同符号のとき、第一項は異符号のときと比べて大きくなる。なぜなら
AとBが同符号のときの![]() のほうが
のほうが
AとBが異符号のときの![]() よりも大きいからだ。
よりも大きいからだ。
一方で第二項![]() は変化しない。よって、
は変化しない。よって、
![]() と、
と、![]() は同符号となるから
は同符号となるから
![]() のときは
のときは![]() と言えるので
と言えるので
![]() は、
は、![]() を下回らないので
を下回らないので
![]() のように書ける。
のように書ける。
同様に
![]() のときは
のときは![]() と言えるので
と言えるので
![]() は、
は、![]() を上回らないので
を上回らないので
![]() のように書ける。
のように書ける。
まとめると
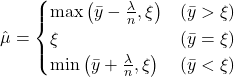
となる。
コード
対数事後分布 h(μ)と、その第1項(観測データに基づく項)および第2項(事前分布に基づく項)のグラフを描画します。パラメータ ξ を 1 または 5、スケールパラメータ λ を 25 または 50 として、それぞれの組み合わせで描画します。
# 2019 Q5(3) 2024.9.29
import numpy as np
import matplotlib.pyplot as plt
# 対数事後分布の第1項: 観測データに基づく項
def h_term1(mu, y):
n = len(y)
y_mean = np.mean(y)
return -0.5 * n * (mu - y_mean)**2
# 対数事後分布の第2項: 事前分布に基づく項
def h_term2(mu, lambd, xi):
return -lambd * np.abs(mu - xi)
# 対数事後分布 h(μ) の定義
def h(mu, y, lambd, xi):
return h_term1(mu, y) + h_term2(mu, lambd, xi)
# μハット(事後分布のモード)を計算
def mu_hat(y_mean, lambd, xi, n):
if y_mean > xi:
return max(y_mean - lambd / n, xi)
elif y_mean < xi:
return min(y_mean + lambd / n, xi)
else:
return xi
# パラメータ設定のリスト (xi, lambd) の組み合わせ
params = [(1, 25), (1, 50), (5, 25), (5, 50)]
n_samples = 20 # サンプル数
mu_values = np.linspace(0, 6, 500) # μの範囲
# グラフを4つ表示するための設定
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
for i, (xi, lambd) in enumerate(params):
# 観測データを生成して、平均を3に調整
np.random.seed(43)
y = np.random.normal(loc=3, scale=1, size=n_samples)
y_mean = np.mean(y)
# μハットを計算
mu_hat_value = mu_hat(y_mean, lambd, xi, n_samples)
# 各項の計算
h_values = h(mu_values, y, lambd, xi)
h_term1_values = h_term1(mu_values, y)
h_term2_values = h_term2(mu_values, lambd, xi)
# サブプロットに描画
ax = axes[i//2, i%2]
ax.plot(mu_values, h_values, label='h(μ)', color='orange')
ax.plot(mu_values, h_term1_values, label='第1項: -n/2 (μ - ȳ)²', color='blue')
ax.plot(mu_values, h_term2_values, label='第2項: -λ|μ - ξ|', color='green')
# μハットを縦線でプロット
ax.axvline(mu_hat_value, color='red', linestyle='--', label=f'μハット = {mu_hat_value:.2f}')
# グラフのタイトル
ax.set_title(f'ξ = {xi}, λ = {lambd}, ȳ = {y_mean:.2f}, n = {n_samples}')
ax.set_xlabel('μ')
ax.set_ylabel('値')
ax.legend()
ax.grid(True)
# グラフを描画
plt.tight_layout()
plt.show()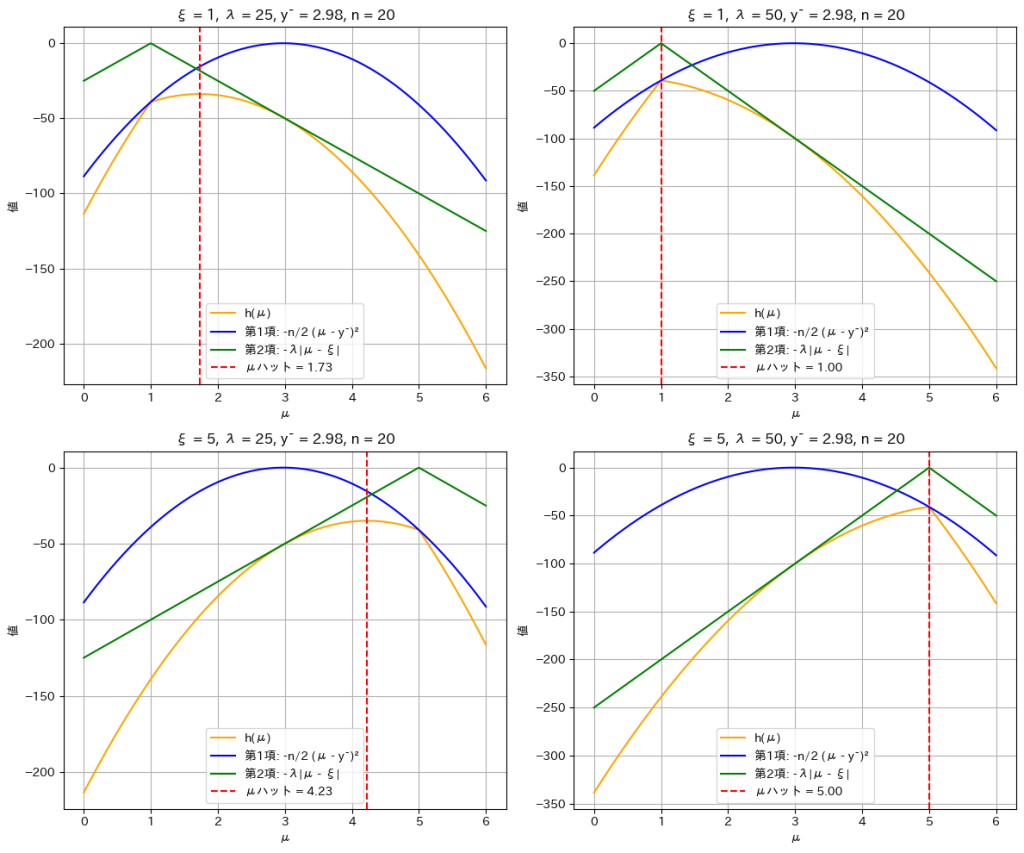
対数事後分布 h(μ)が最大値を取るμハットが
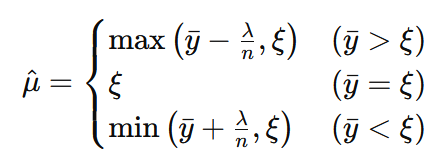
であることが確認できました。
2019 Q5(2)
ラプラス分布に従う確率変数μを母平均とする正規分布の観測値からμの事後確率密度関数を求めました。

コード
数式を使って事後確率密度関数g(μ|y)を求めます。
# 2019 Q5(2) 2024.9.28
import sympy as sp
# シンボリック変数の定義
mu, xi, lambd, n = sp.symbols('mu xi lambda n')
y = sp.IndexedBase('y')
i = sp.symbols('i', integer=True)
# ラプラス分布の事前分布
laplace_prior = (lambd / 2) * sp.exp(-lambd * sp.Abs(mu - xi))
# 正規分布の尤度関数
likelihood = (1 / (2 * sp.pi)**(n / 2)) * sp.exp(-sp.Sum((y[i] - mu)**2 / 2, (i, 1, n)))
# 事後分布 (比例定数は無視)
posterior = laplace_prior * likelihood
# 結果を簡略化
posterior_simplified = sp.simplify(posterior)
# 結果を表示
posterior_simplified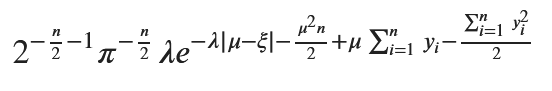
形は少し違いますが手計算の結果と一致しました。
次に、事前分布と事後分布の確率密度関数をプロットします。比較しやすいように事後分布は正規化します。また事前分布がない場合として尤度関数も重ねて描画してみましょう。
# 2019 Q5(2) 2024.9.28
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import simps
# 事前分布(ラプラス分布)の定義
def laplace_prior(mu, xi, lambd):
return (lambd / 2) * np.exp(-lambd * np.abs(mu - xi))
# 事後分布(正規化定数は省略)
def posterior_example(mu, y, xi, lambd):
n = len(y)
y_mean = np.mean(y)
sum_y = np.sum((y - y_mean)**2)
# 解答例の事後分布
return (lambd / (2 * (2 * np.pi)**(n / 2))) * np.exp(-0.5 * (sum_y + n * (mu - y_mean)**2) - lambd * np.abs(mu - xi))
# 尤度関数(事前分布がない場合)
def likelihood(mu, y):
n = len(y)
y_mean = np.mean(y)
return np.exp(-0.5 * n * (mu - y_mean)**2)
# パラメータ設定
xi = 0 # ラプラス分布の中央値
lambd = 1 # スケールパラメータ
n_samples = 20 # サンプル数
# 観測データを生成
np.random.seed(43)
y = np.random.normal(loc=0, scale=1, size=n_samples)
# μの範囲を設定
mu_values = np.linspace(-3, 3, 500)
# 事前分布の計算
prior_values = laplace_prior(mu_values, xi, lambd)
# 事後分布の計算(事前分布あり)
posterior_values_example = posterior_example(mu_values, y, xi, lambd)
# 尤度関数の計算(事前分布なし)
likelihood_values = likelihood(mu_values, y)
# 事後分布と尤度関数を正規化
area_under_curve_example = simps(posterior_values_example, mu_values) # 数値積分
posterior_values_example /= area_under_curve_example # 正規化
area_under_likelihood = simps(likelihood_values, mu_values) # 数値積分
likelihood_values /= area_under_likelihood # 正規化
# グラフをプロット
plt.plot(mu_values, prior_values, label='事前分布 (ラプラス分布)', color='blue')
plt.plot(mu_values, posterior_values_example, label='事後分布', color='purple')
plt.plot(mu_values, likelihood_values, label='尤度関数(事前分布なし)', color='green', linestyle='--')
plt.title('事前分布、事後分布、および事前分布がない場合の尤度関数の比較')
plt.xlabel('μ')
plt.ylabel('確率密度')
plt.legend()
plt.show()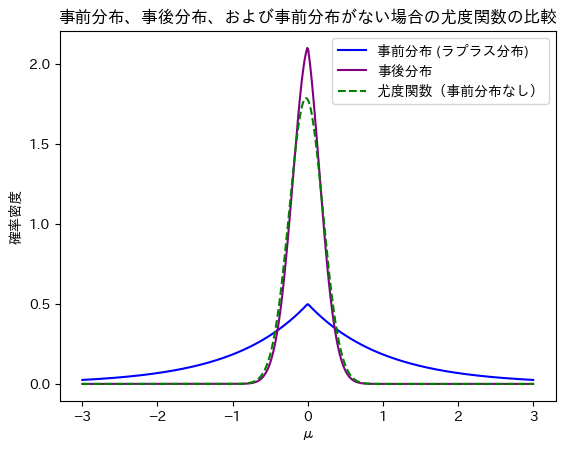
事後分布は事前分布と尤度関数の中間的な形をとっていることが分かります。
2019 Q5(1)-2
ラプラス分布の分散を求めました。
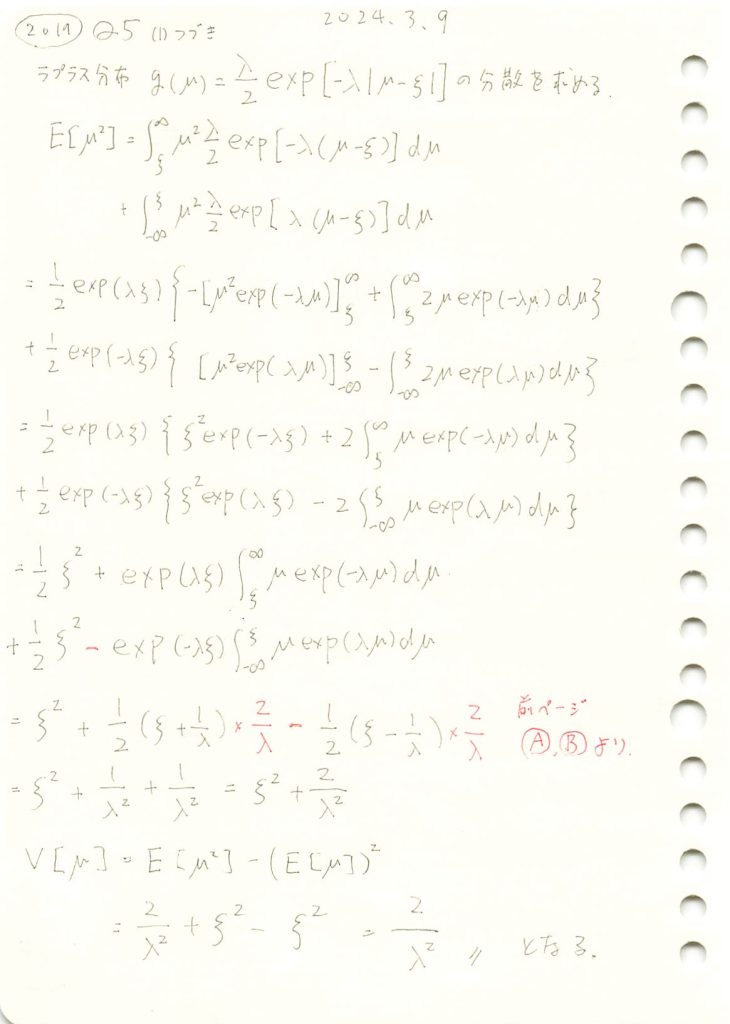
コード
ξ=0,λ=1のラプラス分布 ![]() の期待値E[μ]と分散V[μ]を求めます。
の期待値E[μ]と分散V[μ]を求めます。
# 2019 Q5(1) 2024.9.27
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
xi = 0 # 理論的な期待値
lambda_ = 1 # スケールパラメータ
n_samples = 10000 # サンプル数
# ラプラス分布からランダムサンプルを生成
samples = np.random.laplace(loc=xi, scale=1/lambda_, size=n_samples)
# シミュレーションの期待値と分散を計算
sample_mean = np.mean(samples)
sample_variance = np.var(samples)
# 理論値
theoretical_mean = xi
theoretical_variance = 2 / lambda_**2
# 理論値とシミュレーション値を出力
print(f"シミュレーションによる期待値 E[μ]: {sample_mean}")
print(f"理論的な期待値 E[μ]: {theoretical_mean}")
print(f"シミュレーションによる分散 V[μ]: {sample_variance}")
print(f"理論的な分散 V[μ]: {theoretical_variance}")
# 理論的なラプラス分布のPDFを描画
mu_values = np.linspace(-10, 10, 1000)
pdf_values = (lambda_ / 2) * np.exp(-lambda_ * np.abs(mu_values - xi))
# ヒストグラムの描画
plt.hist(samples, bins=50, density=True, alpha=0.6, color='g', label='シミュレーションデータ')
# 理論的なPDFを線で描画
plt.plot(mu_values, pdf_values, 'r-', lw=2, label='理論的なPDF')
# グラフの設定
plt.title('ラプラス分布:シミュレーション vs 理論的なPDF')
plt.xlabel('値')
plt.ylabel('密度')
plt.legend()
plt.show()シミュレーションによる期待値 E[μ]: -8.093411765355611e-05
理論的な期待値 E[μ]: 0
シミュレーションによる分散 V[μ]: 2.043434597873531
理論的な分散 V[μ]: 2.0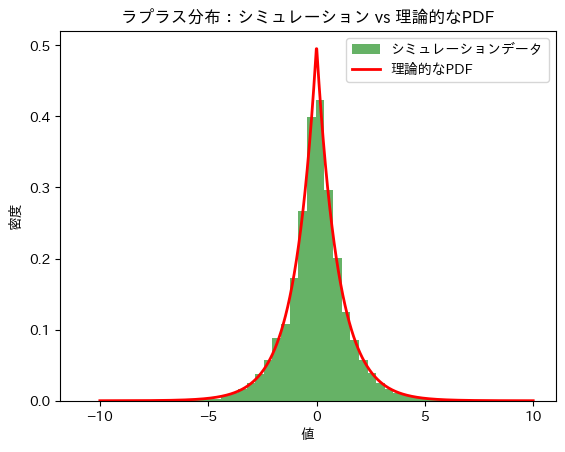
シミュレーションによる期待値E[μ]と分散V[μ]は理論値に近い値をとりました。
2019 Q5(1)-1
ラプラス分布の期待値を求めました。

コード
ξ=0,λ=1のラプラス分布 ![]() の期待値E[μ]と分散V[μ]を求めます。
の期待値E[μ]と分散V[μ]を求めます。
# 2019 Q5(1) 2024.9.27
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
xi = 0 # 理論的な期待値
lambda_ = 1 # スケールパラメータ
n_samples = 10000 # サンプル数
# ラプラス分布からランダムサンプルを生成
samples = np.random.laplace(loc=xi, scale=1/lambda_, size=n_samples)
# シミュレーションの期待値と分散を計算
sample_mean = np.mean(samples)
sample_variance = np.var(samples)
# 理論値
theoretical_mean = xi
theoretical_variance = 2 / lambda_**2
# 理論値とシミュレーション値を出力
print(f"シミュレーションによる期待値 E[μ]: {sample_mean}")
print(f"理論的な期待値 E[μ]: {theoretical_mean}")
print(f"シミュレーションによる分散 V[μ]: {sample_variance}")
print(f"理論的な分散 V[μ]: {theoretical_variance}")
# 理論的なラプラス分布のPDFを描画
mu_values = np.linspace(-10, 10, 1000)
pdf_values = (lambda_ / 2) * np.exp(-lambda_ * np.abs(mu_values - xi))
# ヒストグラムの描画
plt.hist(samples, bins=50, density=True, alpha=0.6, color='g', label='シミュレーションデータ')
# 理論的なPDFを線で描画
plt.plot(mu_values, pdf_values, 'r-', lw=2, label='理論的なPDF')
# グラフの設定
plt.title('ラプラス分布:シミュレーション vs 理論的なPDF')
plt.xlabel('値')
plt.ylabel('密度')
plt.legend()
plt.show()シミュレーションによる期待値 E[μ]: -8.093411765355611e-05
理論的な期待値 E[μ]: 0
シミュレーションによる分散 V[μ]: 2.043434597873531
理論的な分散 V[μ]: 2.0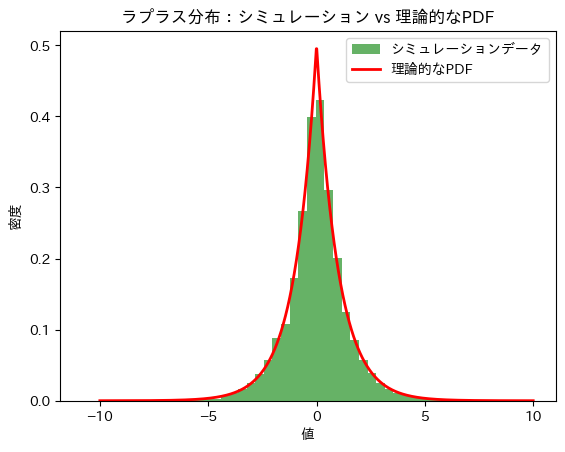
シミュレーションによる期待値E[μ]と分散V[μ]は理論値に近い値をとりました。
2019 Q4(4)
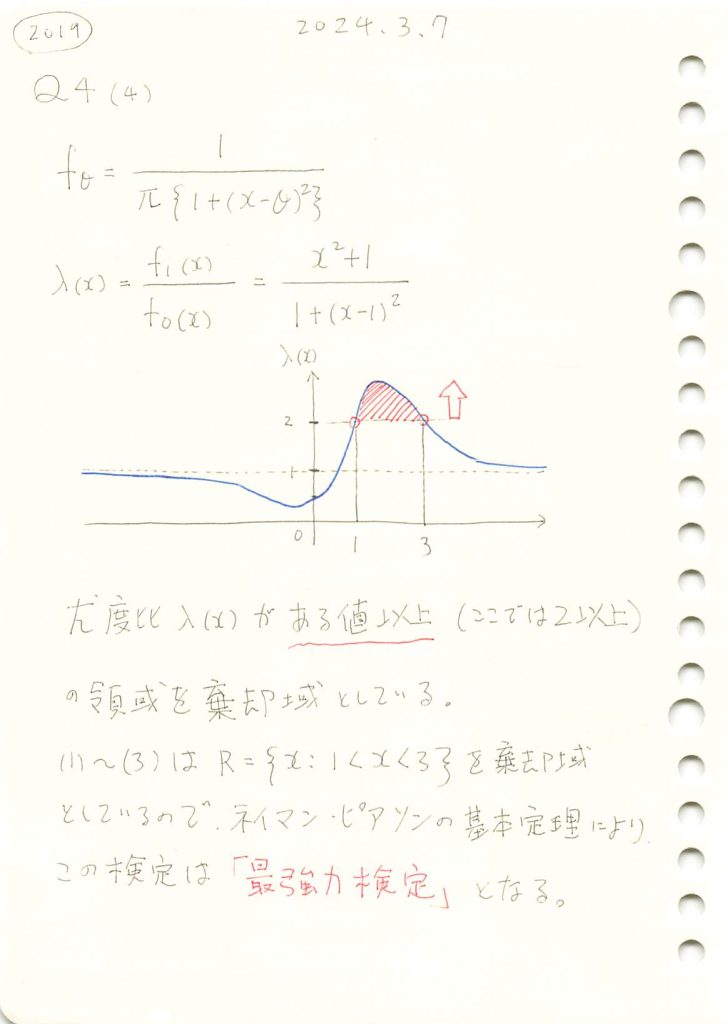
コーシー分布の検定で、与えられた棄却域が最強力検定になることを示しました。
コード
棄却域をR={x:1<x<3}にする検定が最強力検定になるのか確認するために、尤度比λ(x)のグラフを描画します。
# 2019 Q4(4) 2024.9.26
import numpy as np
import matplotlib.pyplot as plt
# 尤度比 λ(x) の計算
def likelihood_ratio(x):
return (1 + x**2) / (1 + (x - 1)**2)
# x の範囲を設定
x_values = np.linspace(-5, 5, 500)
# λ(x) の値を計算
lambda_values = likelihood_ratio(x_values)
# グラフを描画
plt.figure(figsize=(10, 6))
plt.plot(x_values, lambda_values, label=r'尤度比 $\lambda(x) = \frac{1 + x^2}{1 + (x - 1)^2}$', color='b')
# 棄却域 1 < x < 3 を塗りつぶす(透明度を追加)
plt.axvspan(1, 3, color='yellow', alpha=0.3, label=r'棄却域 $1 < x < 3$')
# λ(x) >= 2 の部分を赤で塗る
plt.fill_between(x_values, lambda_values, 2, where=(lambda_values >= 2), color='red', alpha=0.3, label=r'$\lambda(x) \geq 2$')
# グラフの装飾
plt.axhline(2, color='green', linestyle='--', label=r'閾値 $\lambda(x) = 2$')
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title(r'尤度比 $\lambda(x)$ と棄却域 $1 < x < 3$, $\lambda(x) \geq 2$ の範囲')
plt.xlabel('x')
plt.ylabel(r'$\lambda(x)$')
plt.grid(True)
plt.legend()
# グラフを表示
plt.show()
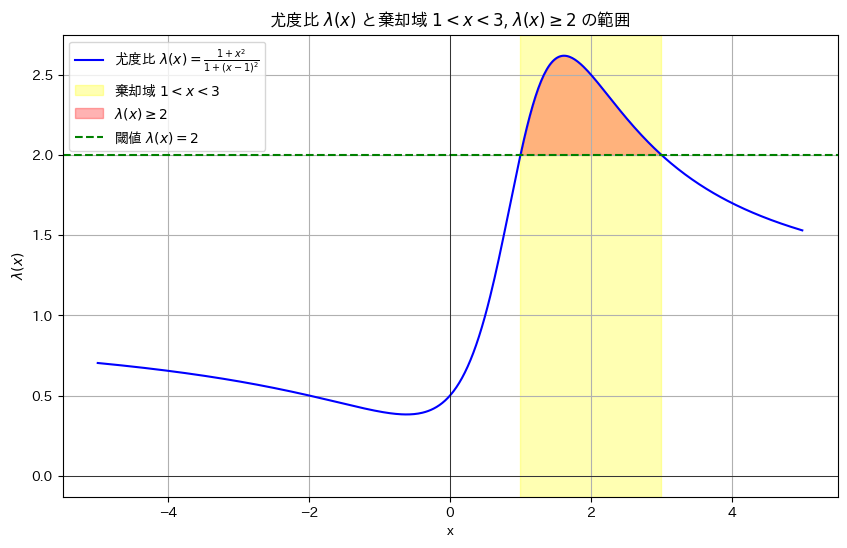
棄却域は尤度比λ(x)>c (ここではc=2)で定義できるので、これは最強力検定と言えます。
ところでx->-∞で尤度比λ(x)はどこに収束するのでしょうか。
import numpy as np
import matplotlib.pyplot as plt
# 尤度比 λ(x) の計算
def likelihood_ratio(x):
return (1 + x**2) / (1 + (x - 1)**2)
# x の範囲を設定(左側を広げる)
x_values = np.linspace(-50, 5, 500)
# λ(x) の値を計算
lambda_values = likelihood_ratio(x_values)
# グラフを描画
plt.figure(figsize=(10, 6))
plt.plot(x_values, lambda_values, label=r'尤度比 $\lambda(x) = \frac{1 + x^2}{1 + (x - 1)^2}$', color='b')
# 閾値を視覚化
plt.axhline(1, color='purple', linestyle='--', label=r'極限 $\lambda(x) \to 1$ as $x \to -\infty$')
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title(r'尤度比 $\lambda(x)$ の概形 ($x \to -\infty$ の範囲)')
plt.xlabel('x')
plt.ylabel(r'$\lambda(x)$')
plt.grid(True)
plt.legend()
# グラフを表示
plt.show()
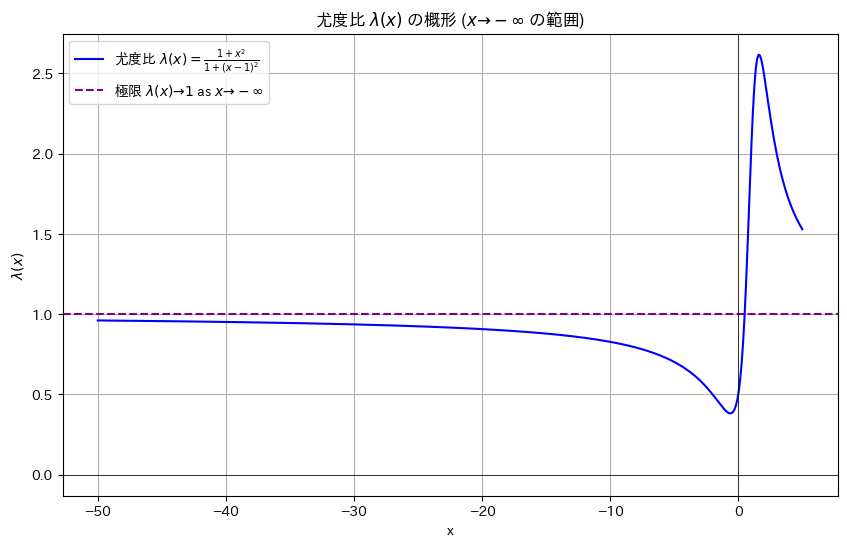
1.0に収束するようです。
よって、cは1以上で、且つ尤度比λ(x)が最大となるx = 1.61803398874989(黄金比)が棄却域に含まれていれば最強力検定になります。
2019 Q4(3)
コーシー分布のパラメータ違いの尤度比の概形を描きました。
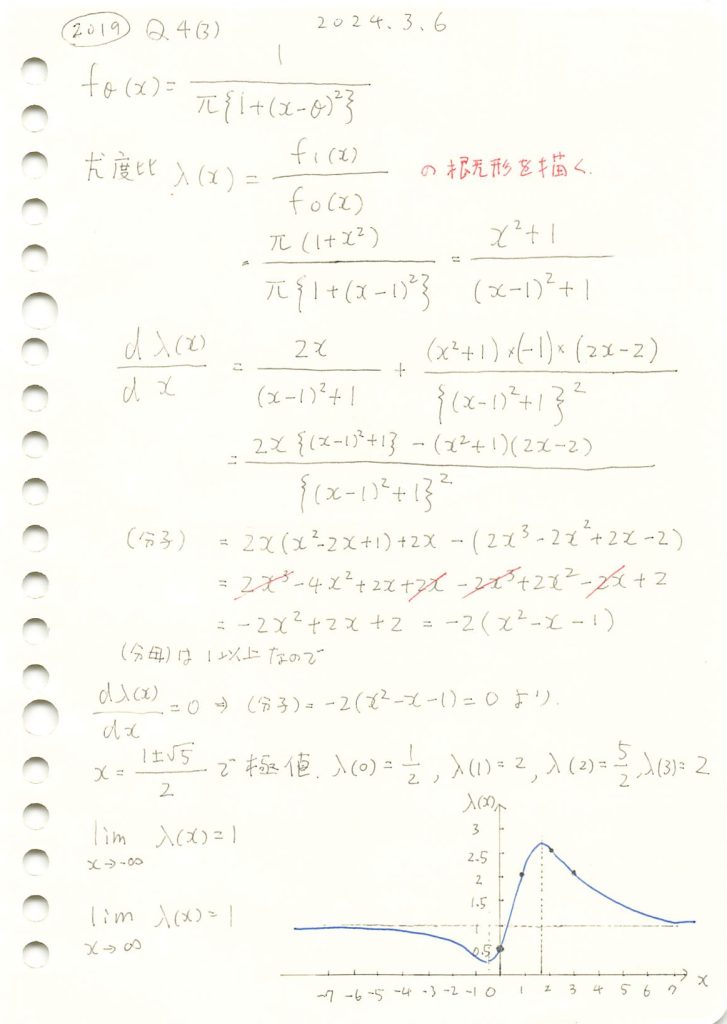
コード
尤度比λ(x)のグラフを描画します。
# 2019 Q4(3) 2024.9.25
import numpy as np
import matplotlib.pyplot as plt
# 尤度比 λ(x) の計算
def likelihood_ratio(x):
return (1 + x**2) / (1 + (x - 1)**2)
# x の範囲を設定
x_values = np.linspace(-5, 5, 500)
# λ(x) の値を計算
lambda_values = likelihood_ratio(x_values)
# グラフを描画
plt.figure(figsize=(10, 6))
plt.plot(x_values, lambda_values, label=r'尤度比 $\lambda(x) = \frac{1 + x^2}{1 + (x - 1)^2}$', color='b')
plt.scatter([1, 3], [2, 2], color='red', zorder=5) # x = 1 および x = 3 の点をプロット
# グラフの装飾
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title(r'尤度比 $\lambda(x)$ の概形')
plt.xlabel('x')
plt.ylabel(r'$\lambda(x)$')
plt.grid(True)
plt.legend()
# グラフを表示
plt.show()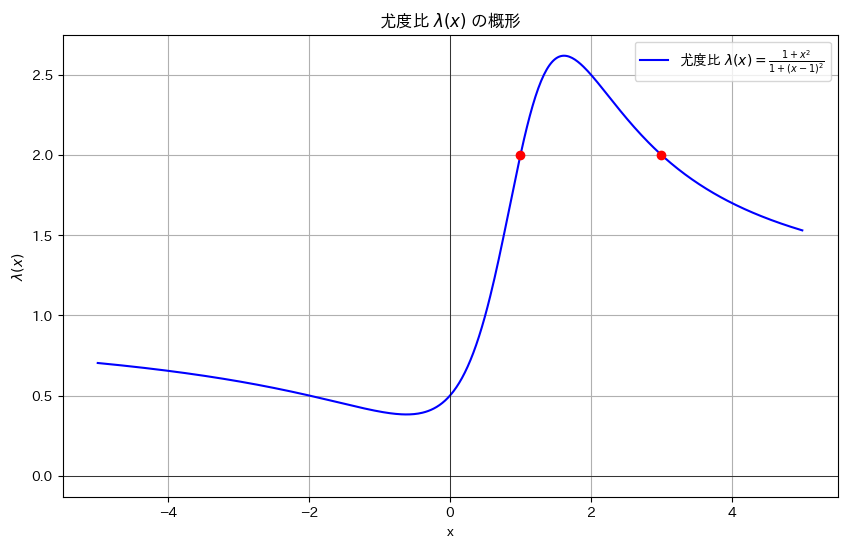
谷と山を持つ形状をしています。
次に、尤度関数λ(x)の1次導関数と2次導関数から、極値と形状(山か谷か)を導きます。
# 2019 Q4(3) 2024.9.25
import sympy as sp
from IPython.display import display
# 尤度比 λ(x) の式を定義
x = sp.symbols('x')
lambda_x = (1 + x**2) / (1 + (x - 1)**2)
# 1次導関数を計算
lambda_prime = sp.diff(lambda_x, x)
print("1次導関数 λ'(x):")
display(lambda_prime)
print()
# 1次導関数が0となる点(極値候補)を解く
critical_points = sp.solve(lambda_prime, x)
print("極値候補:")
display(critical_points)
print()
# 2次導関数を計算して極値の性質を確認
lambda_double_prime = sp.diff(lambda_prime, x)
print("2次導関数 λ''(x):")
display(lambda_double_prime)
print()
# 各極値候補の 2次導関数の値を調べる
for point in critical_points:
second_derivative_value = lambda_double_prime.subs(x, point)
# 極値の場所を数値評価する
point_value = point.evalf()
# 2次導関数の値も数値評価する
second_derivative_value_numeric = second_derivative_value.evalf()
if second_derivative_value > 0:
print(f"x = {point} で谷(極小値) (数値: {point_value})")
print(f"2次導関数の値: {second_derivative_value_numeric}")
elif second_derivative_value < 0:
print(f"x = {point} で山(極大値) (数値: {point_value})")
print(f"2次導関数の値: {second_derivative_value_numeric}")
else:
print(f"x = {point} で特異点か平坦な極値 (数値: {point_value})")
print(f"2次導関数の値: {second_derivative_value_numeric}")
以上のように求まりました。
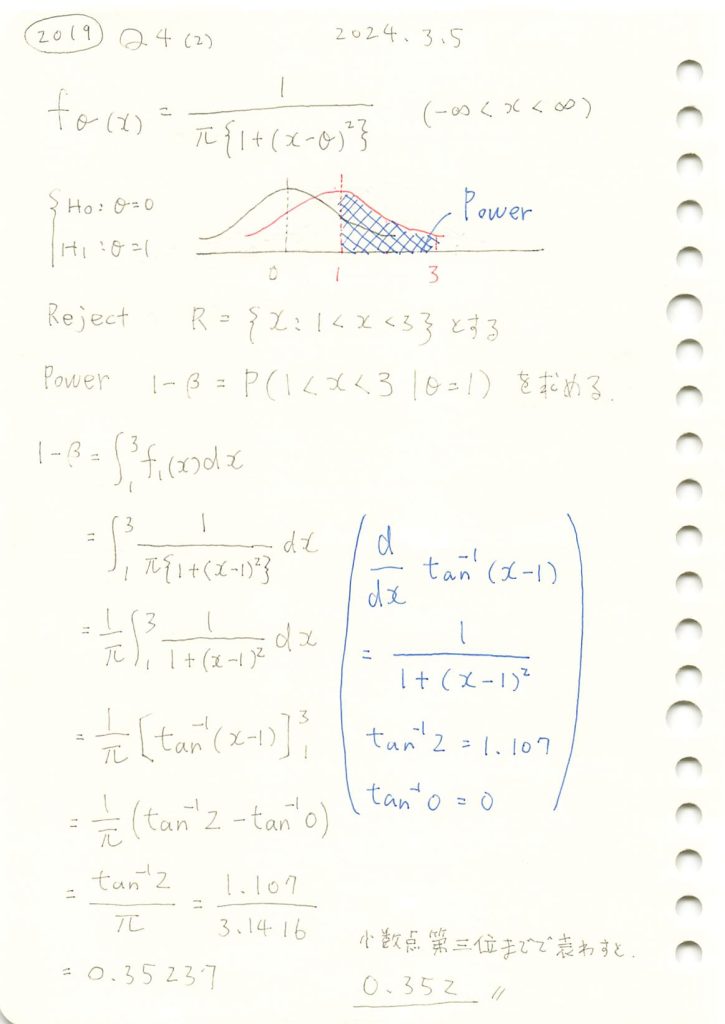
2019 Q4(2)
コーシー分布の検出力を計算しました。
コード
数式を使って検出力1-βを求めます。
# 2019 Q4(2) 2024.9.24
import numpy as np
from scipy.integrate import quad
# コーシー分布の確率密度関数 (theta = 1)
def cauchy_pdf_theta_1(x):
return 1 / (np.pi * (1 + (x - 1)**2))
# 積分範囲(棄却域R = (1, 3))
lower_bound = 1
upper_bound = 3
# 積分を実行
power, error = quad(cauchy_pdf_theta_1, lower_bound, upper_bound)
# 結果を表示(小数第3位まで表示)
print(f"検出力 (1 - β): {power:.3f}")検出力 (1 - β): 0.352手計算と一致しました。
次に、数値シミュレーションで計算をしてみます。なお、コーシー分布は裾が重いため-8 ~8の範囲になるようにフィルターを掛けることにします。
# 2019 Q4(2) 2024.9.24
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import cauchy
# シミュレーションのパラメータ
np.random.seed(43)
num_trials = 100000
# 棄却域 R = (1, 3)
lower_bound = 1
upper_bound = 3
# コーシー分布 (θ = 1) からのサンプルを生成
samples = cauchy.rvs(loc=1, scale=1, size=num_trials)
# -8 から 8 の範囲にサンプルを制限して外れ値を除外
filtered_samples = samples[(samples > -8) & (samples < 8)]
# 棄却域に入っているかどうかを判定
reject = (samples > lower_bound) & (samples < upper_bound)
# 棄却域に入った割合が検出力 (1 - β)
power_simulated = np.mean(reject)
# 結果を表示
print(f"シミュレーションによる検出力 (1 - β): {power_simulated:.3f}")
# ヒストグラムのプロット(フィルタリングしたサンプルを使う)
plt.figure(figsize=(10, 6))
plt.hist(filtered_samples, bins=100, density=True, alpha=0.5, color='blue', label='シミュレーション結果(フィルタリング済み)')
# 理論的なコーシー分布の確率密度関数 (theta = 1) をプロット
x = np.linspace(-8, 8, 1000)
pdf_theta_1 = cauchy.pdf(x, loc=1) # 対立仮説の理論曲線 (θ = 1)
plt.plot(x, pdf_theta_1, 'r-', lw=2, label='理論的コーシー分布 (θ = 1)')
# 理論的なコーシー分布の確率密度関数 (theta = 0) をプロット
pdf_theta_0 = cauchy.pdf(x, loc=0) # 帰無仮説の理論曲線 (θ = 0)
plt.plot(x, pdf_theta_0, 'g--', lw=2, label='理論的コーシー分布 (θ = 0)')
# 棄却域を塗りつぶす
plt.axvspan(lower_bound, upper_bound, color='red', alpha=0.3, label='棄却域 (1 < x < 3)')
# グラフの設定
plt.xlim(-8, 8)
plt.xlabel('x')
plt.ylabel('密度')
plt.title(f'コーシー分布のシミュレーションと棄却域\nシミュレーションによる検出力 (1 - β) = {power_simulated:.3f}')
plt.legend()
plt.grid(True)
# グラフを表示
plt.show()シミュレーションによる検出力 (1 - β): 0.355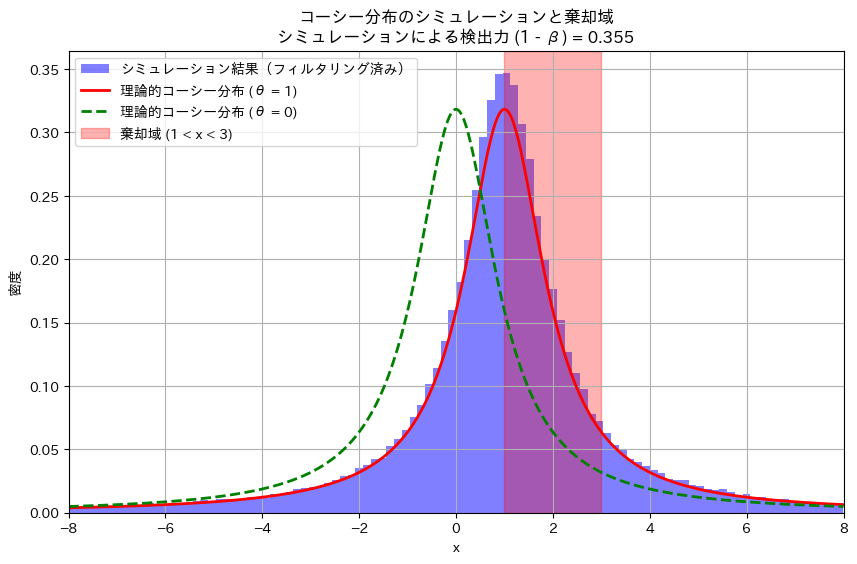
シミュレーション結果も手計算とほぼ一致しました。
2019 Q4(1)
コーシー分布の検定での第一種過誤確率を求めました。
コード
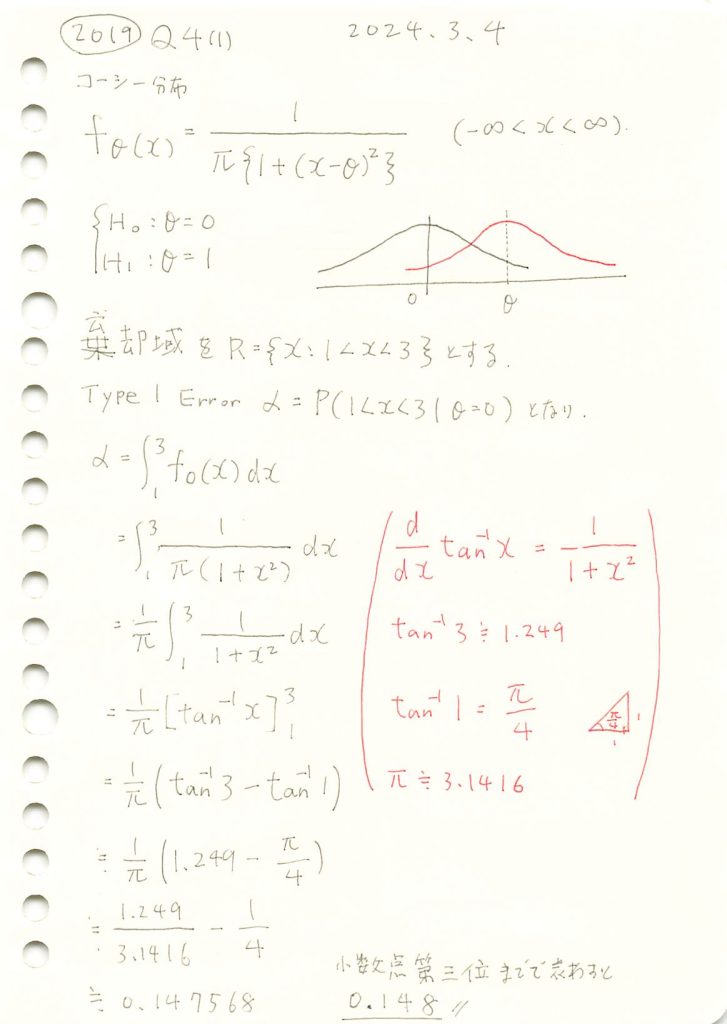
数式を使って第一種の過誤確率αを求めます。
# 2019 Q4(1) 2024.9.23
import numpy as np
from scipy.integrate import quad
# コーシー分布の確率密度関数 (theta = 0)
def cauchy_pdf(x):
return 1 / (np.pi * (1 + x**2))
# 積分範囲(棄却域R = (1, 3))
lower_bound = 1
upper_bound = 3
# 積分を実行
alpha, error = quad(cauchy_pdf, lower_bound, upper_bound)
# 結果を表示(小数第3位まで表示)
print(f"第一種の過誤確率 α: {alpha:.3f}")第一種の過誤確率 α: 0.148手計算と一致しました。
次に、数値シミュレーションで計算をしてみます。なお、コーシー分布は裾が重いため-8 ~8の範囲になるようにフィルターを掛けることにします。
# 2019 Q4(1) 2024.9.23
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import cauchy
# シミュレーションのパラメータ
np.random.seed(43)
num_trials = 100000
# 棄却域 R = (1, 3)
lower_bound = 1
upper_bound = 3
# コーシー分布 (θ = 0) からのサンプルを生成
samples = np.random.standard_cauchy(size=num_trials)
# -8 から 8 の範囲にサンプルを制限して外れ値を除外
filtered_samples = samples[(samples > -8) & (samples < 8)]
# 棄却域に入っているかどうかを判定
reject = (samples > lower_bound) & (samples < upper_bound)
# 棄却域に入った割合が第一種の過誤確率 α
alpha_simulated = np.mean(reject)
# 結果を表示
print(f"シミュレーションによる第一種の過誤確率 α: {alpha_simulated:.3f}")
# ヒストグラムのプロット(フィルタリングしたサンプルを使う)
plt.figure(figsize=(10, 6))
plt.hist(filtered_samples, bins=100, density=True, alpha=0.5, color='blue', label='シミュレーション結果(フィルタリング済み)')
# 理論的なコーシー分布の確率密度関数 (theta = 0) をプロット
x = np.linspace(-8, 8, 1000) # 横のレンジを -8 から 8 に設定
pdf = cauchy.pdf(x)
plt.plot(x, pdf, 'r-', lw=2, label='理論的コーシー分布の確率密度関数')
# 棄却域を塗りつぶす
plt.axvspan(lower_bound, upper_bound, color='red', alpha=0.3, label='棄却域 (1 < x < 3)')
# グラフの設定
plt.xlim(-8, 8) # 横のレンジを -8 から 8 に設定
plt.xlabel('x')
plt.ylabel('密度')
plt.title(f'コーシー分布のシミュレーションと棄却域\nシミュレーションによる α = {alpha_simulated:.3f}')
plt.legend()
plt.grid(True)
# グラフを表示
plt.show()シミュレーションによる第一種の過誤確率 α: 0.148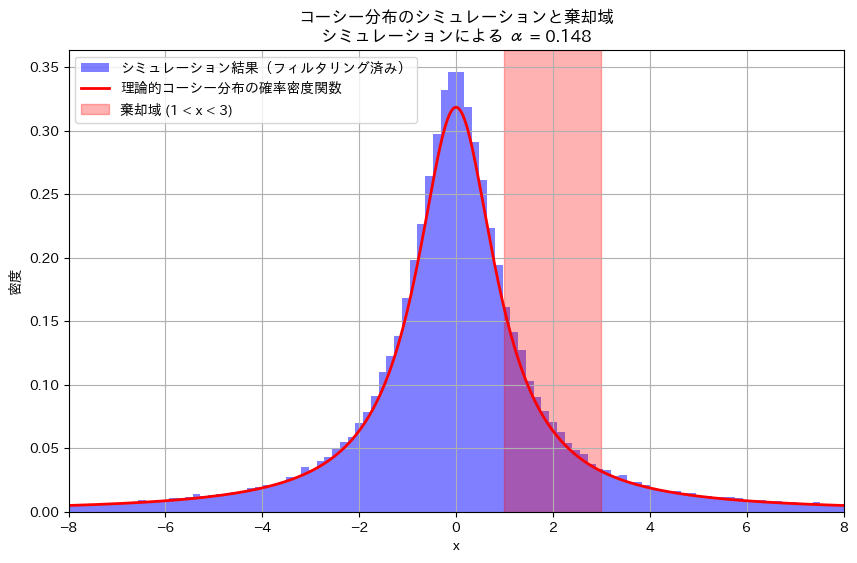
シミュレーション結果も手計算と一致しました。
2019 Q3(6)
唯一の不偏推定量であることを示しました。

コード
![]() は、Yによるθの唯一の不偏推定量になります。またYはθの十分統計量ですから、完備十分統計量となります。よって、
は、Yによるθの唯一の不偏推定量になります。またYはθの十分統計量ですから、完備十分統計量となります。よって、![]() は、最小分散不偏推定量(UMVUE)となります。他のθの推定量
は、最小分散不偏推定量(UMVUE)となります。他のθの推定量![]() と一緒にプロットし分散を確認します。
と一緒にプロットし分散を確認します。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真のθ
n = 10 # サンプルサイズ
num_simulations = 10000 # シミュレーション回数
# UMVUE(最大値を使った推定量)の格納リスト
theta_hat_UMVUE_list = []
# 他の推定量(例えば、平均を使った推定量)の格納リスト
theta_hat_mean_list = []
# シミュレーション開始
for _ in range(num_simulations):
# U(0, theta_true) から n 個の乱数を生成
samples = np.random.uniform(0, theta_true, n)
# 最大値 Y を使用して UMVUE を計算
Y = np.max(samples)
theta_hat_UMVUE = (n + 1) / n * Y
theta_hat_UMVUE_list.append(theta_hat_UMVUE)
# 平均を使用して他の推定量を計算
theta_hat_mean = 2 * np.mean(samples)
theta_hat_mean_list.append(theta_hat_mean)
# UMVUE 推定量の分散を計算
umvue_variance = np.var(theta_hat_UMVUE_list)
# 平均推定量の分散を計算
mean_variance = np.var(theta_hat_mean_list)
# 結果を表示
print(f"UMVUE(最大値を使った推定量)の分散: {umvue_variance}")
print(f"平均を使った推定量の分散: {mean_variance}")
# 推定量の分布をプロット
plt.hist(theta_hat_UMVUE_list, bins=30, alpha=0.7, label='UMVUE(最大値を使用)', color='blue', edgecolor='black', density=True)
plt.hist(theta_hat_mean_list, bins=30, alpha=0.7, label='平均を使用した推定量', color='red', edgecolor='black', density=True)
plt.title('UMVUE(最大値)と平均推定量の分布比較')
plt.xlabel('推定量の値')
plt.ylabel('密度')
plt.legend()
plt.grid(True)
plt.show()UMVUE(最大値を使った推定量)の分散: 0.8726264971281747
平均を使った推定量の分散: 3.3430162264024963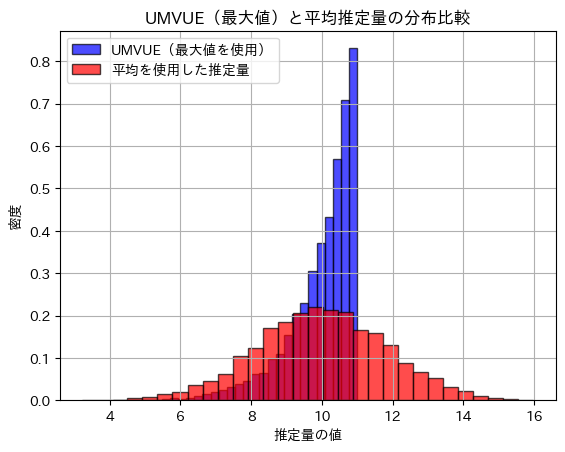
![]() の分散は、
の分散は、![]() の分散よりも小さいことが確認できました。
の分散よりも小さいことが確認できました。