ホーム » 統計検定1級 2018年 統計数理 (ページ 2)
「統計検定1級 2018年 統計数理」カテゴリーアーカイブ
2018 Q3(2)
二項分布の条件付き確率質量関数を求めました。

コード
条件付き二項分布のシミュレーションを行い理論値と一致するか確認します。
# 2018 Q3(2) 2024.10.12
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 10 # 試行回数
theta = 0.5 # 成功確率
num_simulations = 10000 # シミュレーション回数
# 二項分布に従うランダム変数を生成
binom_samples = np.random.binomial(n, theta, num_simulations)
# X >= 1 の条件を満たすサンプルを抽出
samples_X_geq_1 = binom_samples[binom_samples >= 1]
# X = x の回数を数える
counts, _ = np.histogram(samples_X_geq_1, bins=np.arange(n+2))
# シミュレーションによる条件付き確率(X = 1 から n の範囲で計算)
simulated_probabilities = counts[1:] / np.sum(counts)
# 理論上の条件付き確率 h(x)
x_values = np.arange(1, n+1)
binom_pmf = np.array([np.math.comb(n, x) * theta**x * (1-theta)**(n-x) for x in x_values])
theoretical_probabilities = binom_pmf / (1 - (1 - theta)**n)
# シミュレーション結果をヒストグラムで表示
plt.bar(x_values, simulated_probabilities, color='blue', alpha=0.6, label="シミュレーション")
plt.plot(x_values, theoretical_probabilities, label="理論値", marker='x', linestyle='-', color='red')
# グラフの描画
plt.xlabel("X の値", fontsize=12)
plt.ylabel("条件付き確率 P(X = x | X >= 1)", fontsize=12)
plt.title(f"条件付き確率のシミュレーションと理論値の比較 (n={n}, θ={theta})", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()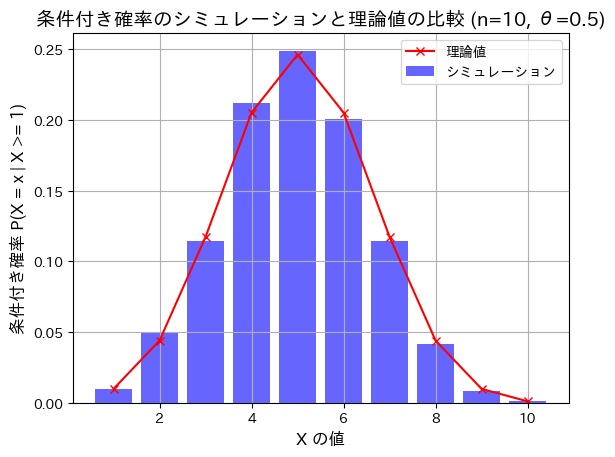
シミュレーションによる結果と理論値が一致しました。
2018 Q3(1)
二項分布の期待値と分散を求めました。
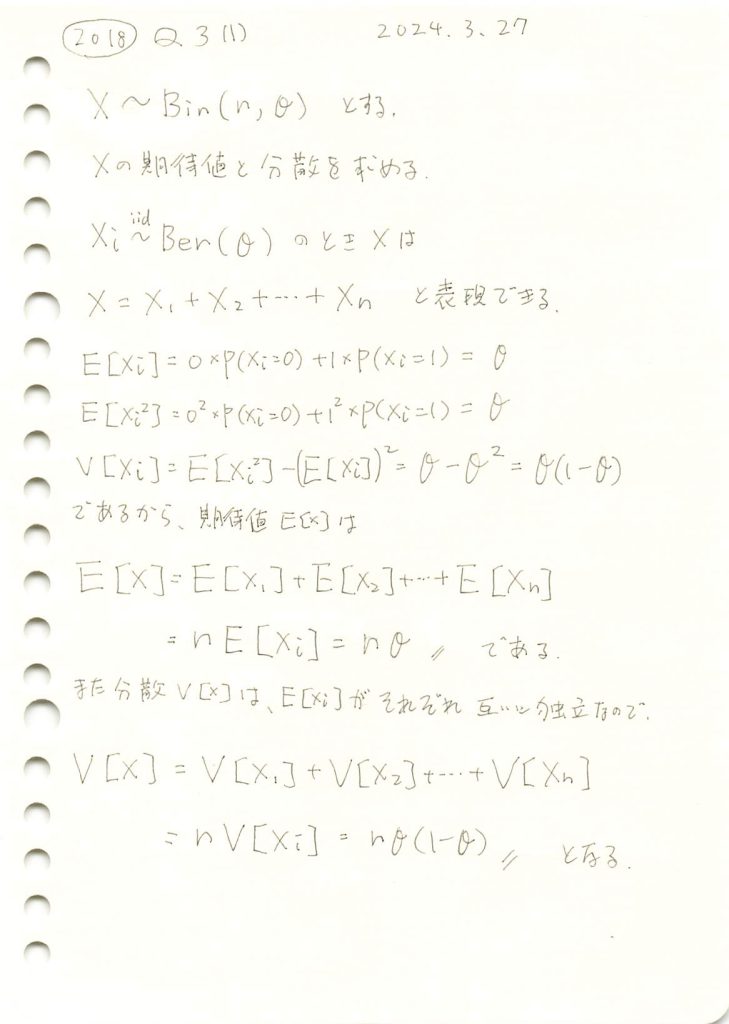
コード
ベルヌーイ試行による二項分布のシミュレーションを行い二項分布の期待値と分散を求めます。
# 2018 Q3(1) 2024.10.11
import numpy as np
import matplotlib.pyplot as plt
# パラメータ
n = 10 # 試行回数
theta = 0.5 # 成功確率
num_simulations = 10000 # シミュレーションの回数
# シミュレーションを実行
bernoulli_trials = np.random.binomial(1, theta, (num_simulations, n))
# 各シミュレーションでの X = X1 + X2 + ... + Xn を計算
X_values = np.sum(bernoulli_trials, axis=1)
# 期待値と分散を計算
simulated_mean = np.mean(X_values)
simulated_variance = np.var(X_values)
# 理論値
theoretical_mean = n * theta
theoretical_variance = n * theta * (1 - theta)
# 結果を表示
print(f"シミュレーションによる期待値: {simulated_mean}")
print(f"理論上の期待値: {theoretical_mean}")
print(f"シミュレーションによる分散: {simulated_variance}")
print(f"理論上の分散: {theoretical_variance}")
# ヒストグラムを描画
plt.hist(X_values, bins=np.arange(n+2)-0.5, density=True, alpha=0.75, color='blue', edgecolor='black')
plt.title("ベルヌーイ試行による二項分布のシミュレーション")
plt.xlabel("Xの値 (成功回数)")
plt.ylabel("確率")
plt.show()シミュレーションによる期待値: 4.9827
理論上の期待値: 5.0
シミュレーションによる分散: 2.54300071
理論上の分散: 2.5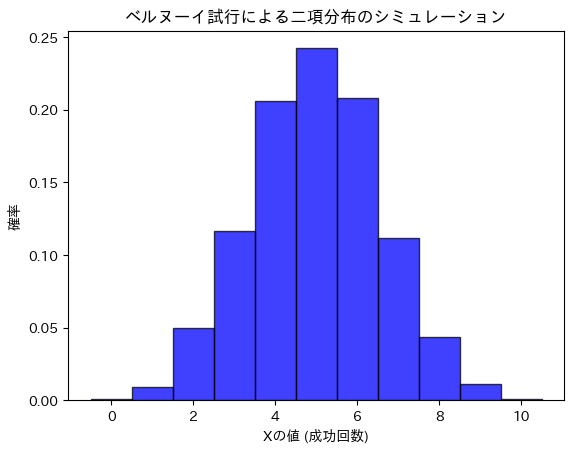
シミュレーションによる結果と理論値が一致しました。
2018 Q2(5)-2
漸近分散の相対標準偏差を求める問題をやりました。

コード
NとMを変化させてシミュレーションし![]() の分布を描画しました。
の分布を描画しました。![]() を求め、理論値と一致するか確認してみます。
を求め、理論値と一致するか確認してみます。
# 2018 Q2(5)-2 2024.10.10
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_true = 1000 # 真の青球の数 N (これを推定する)
K_values = [100, 300, 500] # 赤球の数 K のバリエーション
n_values = [100, 200, 300] # 抽出する回数 n のバリエーション
n_trials = 10000 # シミュレーションの試行回数
# グラフレイアウト設定
fig, axes = plt.subplots(len(K_values), len(n_values), figsize=(15, 12))
axes = axes.flatten()
plot_idx = 0
# 各 K, n の組み合わせに対してシミュレーションを実行
for K in K_values:
for n in n_values:
N_hat_values = []
for _ in range(n_trials):
# 青球 N 個 + 赤球 K 個のボールを作成
balls = [0] * N_true + [1] * K # 0が青球、1が赤球
drawn_balls = np.random.choice(balls, size=n, replace=False) # 非復元抽出
X = np.sum(drawn_balls) # 抽出された赤球の個数
# X を使って N の推定量 N_hat を計算
if X > 0: # Xが0でない場合
N_hat = K * (n - X) / X
N_hat_values.append(N_hat)
# シミュレーション結果から N_hat の分散を計算
N_hat_var = np.var(N_hat_values)
# 理論値 ε の計算
epsilon_theory = np.sqrt((N_true + K) * (N_true + K - n) / (n * N_true * K))
# シミュレーションから求めた ε の計算
epsilon_simulation = np.sqrt(N_hat_var) / N_true
# 推定量 N_hat の分布をヒストグラムで表示
ax = axes[plot_idx]
ax.hist(N_hat_values, bins=100, density=True, alpha=0.7, color='b', edgecolor='black')
ax.axvline(x=N_true, color='r', linestyle='--') # 真の N を破線で表示
ax.set_title(f'K={K}, n={n}')
ax.set_xlabel('推定量 N_hat')
ax.set_ylabel('確率密度')
# εの値と真のNをまとめて表示
ax.text(0.95, 0.95, f'真の N = {N_true}\nε (理論) = {epsilon_theory:.4f}\nε (シミュ) = {epsilon_simulation:.4f}',
transform=ax.transAxes, verticalalignment='top', horizontalalignment='right',
bbox=dict(facecolor='white', alpha=0.7), fontsize=10)
ax.grid(True)
plot_idx += 1
# グラフ全体の調整
plt.tight_layout()
plt.show()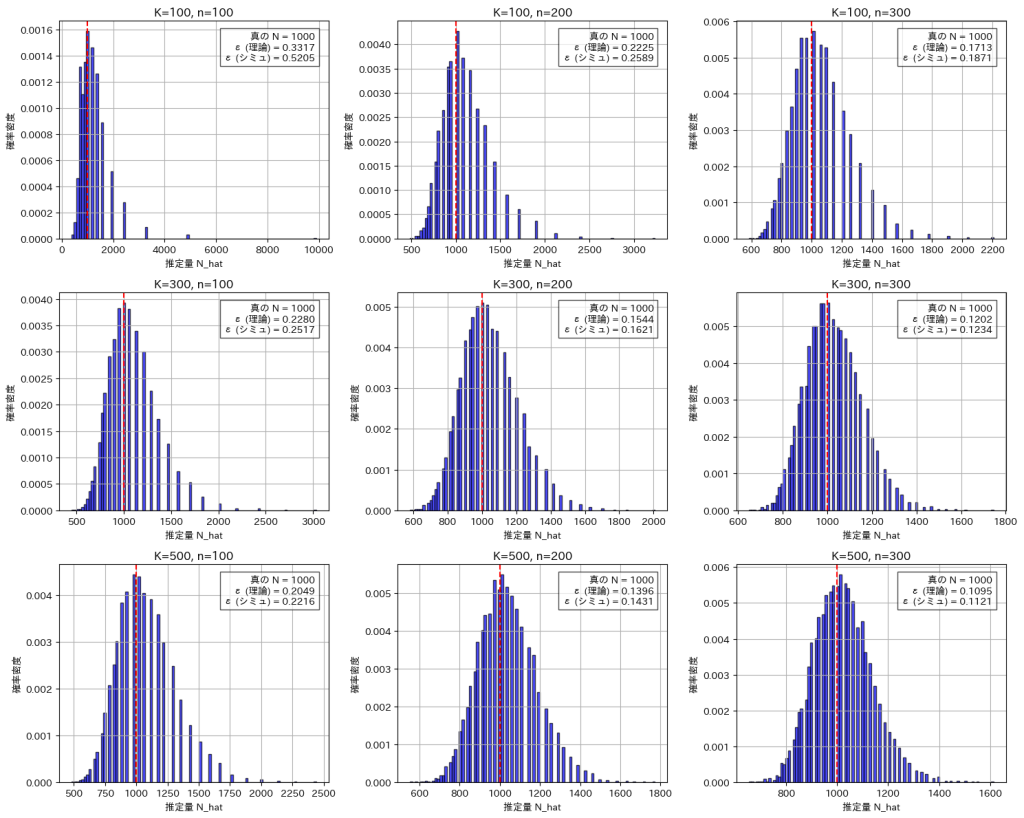
シミュレーションによる結果は理論値と概ね一致しました。
2018 Q2(5)-1
非復元無作為抽出による未知の母数N個の推定を行いました。

コード
複数回シミュレーションし![]() のヒストグラムを描画します。
のヒストグラムを描画します。
# 2018 Q2(5)-1 2024.10.9
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_true = 100 # 真の青球の数 N (これを推定する)
K = 30 # 赤球の数 K (既知)
n = 20 # 抽出する回数
n_trials = 10000 # シミュレーションの試行回数
# 推定量 Nハットのシミュレーション
N_hat_values = []
for _ in range(n_trials):
# 青球 N 個 + 赤球 K 個のボールを作成
balls = [0] * N_true + [1] * K # 0が青球、1が赤球
drawn_balls = np.random.choice(balls, size=n, replace=False) # 非復元抽出
X = np.sum(drawn_balls) # 抽出された赤球の個数
# X を使って N の推定量 N_hat を計算
if X > 0: # Xが0でない場合
N_hat = K * (n - X) / X
N_hat_values.append(N_hat)
# シミュレーション結果の分析
N_hat_mean = np.mean(N_hat_values)
N_hat_var = np.var(N_hat_values)
# 結果表示
print(f"推定量 N_hat の平均: {N_hat_mean}")
print(f"推定量 N_hat の分散: {N_hat_var}")
# ヒストグラム表示
plt.figure(figsize=(10, 6))
plt.hist(N_hat_values, bins=50, density=True, alpha=0.7, color='b', edgecolor='black')
plt.axvline(x=N_true, color='r', linestyle='--', label=f'真の N = {N_true}')
plt.title(f'推定量 N_hat の分布 (N={N_true}, K={K}, n={n})')
plt.xlabel('推定量 N_hat')
plt.ylabel('確率密度')
plt.legend()
plt.grid(True)
plt.show()推定量 N_hat の平均: 126.09541441704363
推定量 N_hat の分散: 8070.195087794488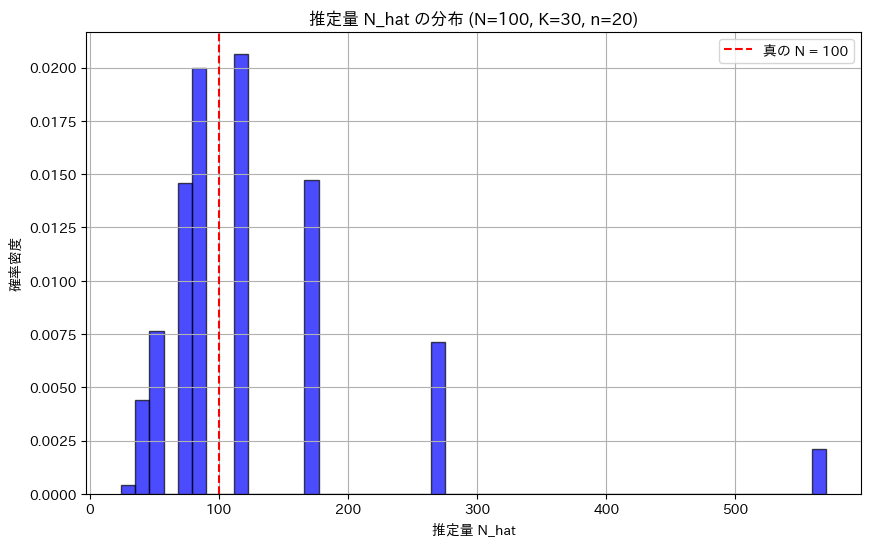
![]() は、真のNから離れた値も取ることがあり、特に飛び飛びの値を取りやすく、右側に裾が長い形をしていることが分かりました。
は、真のNから離れた値も取ることがあり、特に飛び飛びの値を取りやすく、右側に裾が長い形をしていることが分かりました。
2018 Q2(4)
超幾何分布の期待値と分散を求めました。

コード
NとMを変化させて期待値E[X]と分散V[X]についてシミュレーションを行い理論値と一致するか確認します。
# 2018 Q2(4) 2024.10.8
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数
n = 10 # 抽出回数
n_trials = 10000 # シミュレーションの試行回数
# グラフ描画の準備
plt.figure(figsize=(12, 8))
for N in N_values:
M_values = np.arange(M_steps, N + 1, M_steps) # 赤球数をステップで変化
# 理論値の計算
E_X_theory = n * M_values / N
V_X_theory = n * M_values / N * (N - M_values) / N * (N - n) / (N - 1)
# シミュレーションによる期待値と分散の計算
E_X_simulation = []
V_X_simulation = []
for M in M_values:
X_values = []
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M)
drawn_balls = np.random.choice(balls, size=n, replace=False)
X_values.append(np.sum(drawn_balls)) # 赤球の数
E_X_simulation.append(np.mean(X_values))
V_X_simulation.append(np.var(X_values))
# 期待値のグラフに追加描画
plt.subplot(2, 1, 1) # 期待値のグラフ (上側)
plt.plot(M_values, E_X_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, E_X_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
# 分散のグラフに追加描画
plt.subplot(2, 1, 2) # 分散のグラフ (下側)
plt.plot(M_values, V_X_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, V_X_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
# グラフの設定
plt.subplot(2, 1, 1)
plt.xlabel('赤球の数 (M)')
plt.ylabel('期待値 E[X]')
plt.title('異なる N における期待値 E[X] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.subplot(2, 1, 2)
plt.xlabel('赤球の数 (M)')
plt.ylabel('分散 V[X]')
plt.title('異なる N における分散 V[X] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()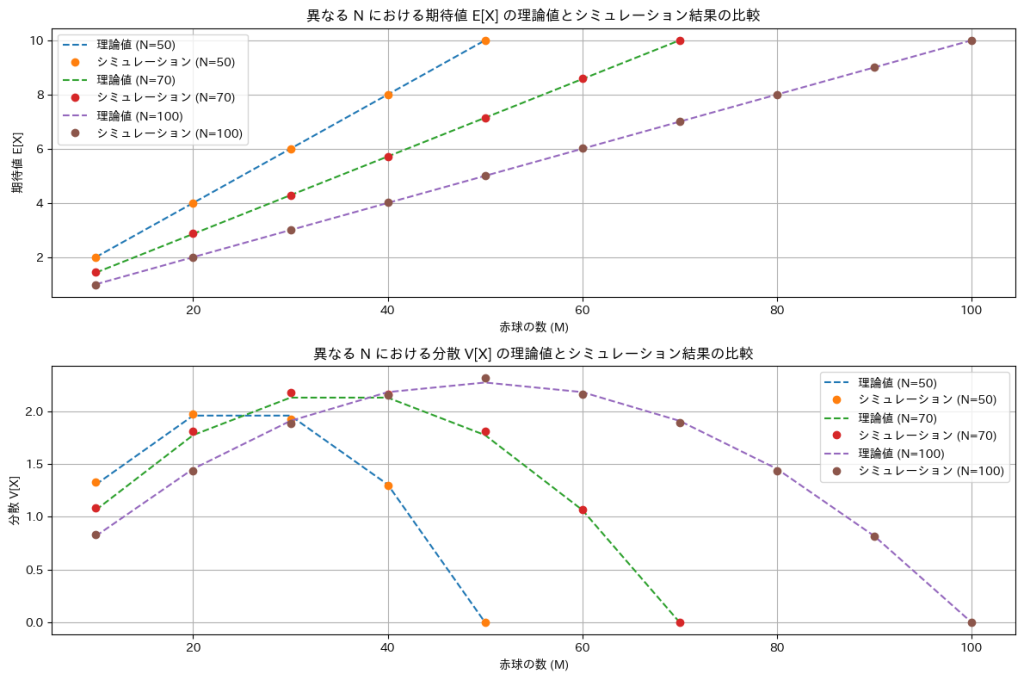
ミュレーションによる結果は理論値と一致しました。
2018 Q2(3)
非復元無作為抽出の当たり数を確率変数とする確率質量関数を求めました。

コード
超幾何分布HG(N,M,n)に従う確率変数XのシミュレーションをNとMを変化させて実行し理論値と一致するか確認してみます。
# 2018 Q2(3) 2024.10.7
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import hypergeom
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション (列ごとに固定)
M_values = [10, 20, 30, 40, 50] # 赤球の数 M のバリエーション (行ごとに変化)
n = 10 # 抽出する回数
n_trials = 10000 # シミュレーションの試行回数
# グラフのレイアウト設定 (5行x3列)
fig, axes = plt.subplots(5, 3, figsize=(15, 20)) # 5行3列のサブプロット
# 各 M に対してシミュレーションと理論値を計算
for row, M in enumerate(M_values): # 行が M を表す
for col, N in enumerate(N_values): # 列が N を表す
# 理論値の計算
x_values = np.arange(0, n + 1) # 可能な赤球の数 x の範囲
rv = hypergeom(N, M, n) # 超幾何分布のインスタンス
P_X_theory = rv.pmf(x_values) # 理論値(超幾何分布)
# シミュレーションによる確率計算
drawn_red_balls = []
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M) # 赤球 M 個、青球 N-M 個のリスト
drawn_balls = np.random.choice(balls, size=n, replace=False) # n 回非復元抽出
x = np.sum(drawn_balls) # 赤球の個数を数える
drawn_red_balls.append(x)
# 各サブプロットにグラフを描画
ax = axes[row, col]
ax.plot(x_values, P_X_theory, 'bo-', label=f'理論値 (N={N}, M={M})')
ax.hist(drawn_red_balls, bins=np.arange(-0.5, n + 1.5, 1), density=True, alpha=0.6, color='r', label='シミュレーション結果')
ax.set_xlabel('赤球の個数 (x)')
ax.set_ylabel('確率 P(X = x)')
ax.set_title(f'N={N}, M={M}, n={n}')
ax.grid(True)
# 全体のレイアウト調整
plt.tight_layout()
plt.show()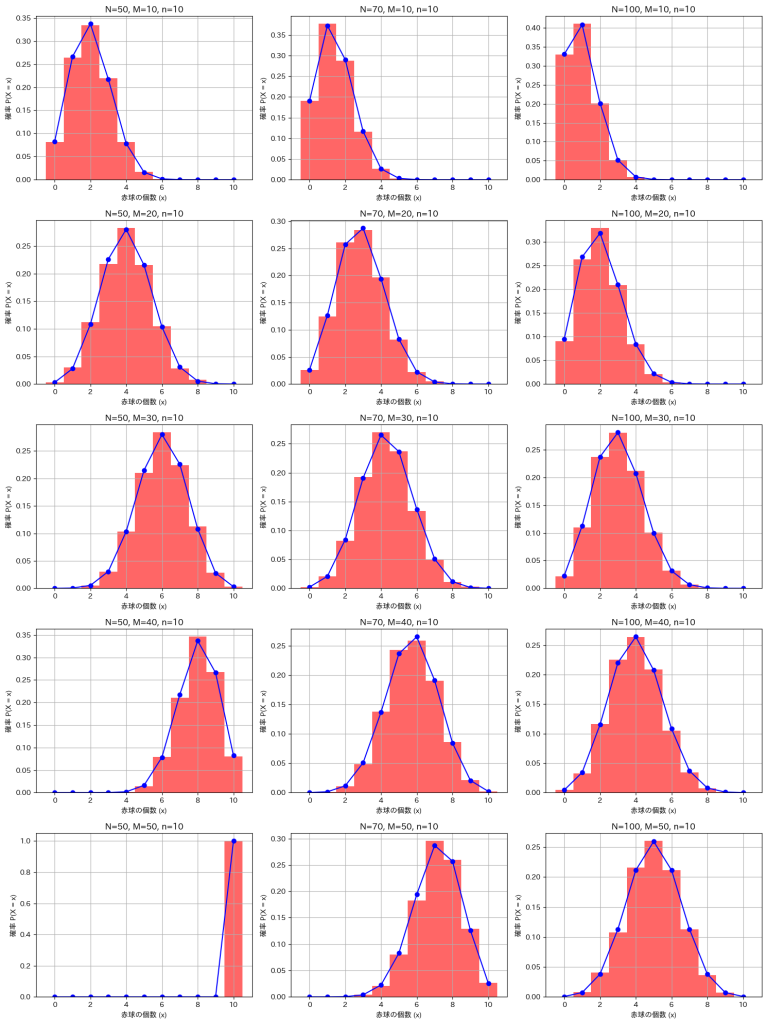
シミュレーションによる結果は理論値と一致しました。
2018 Q2(2)
非復元無作為抽出の期待値と分散と共分散を求めました。
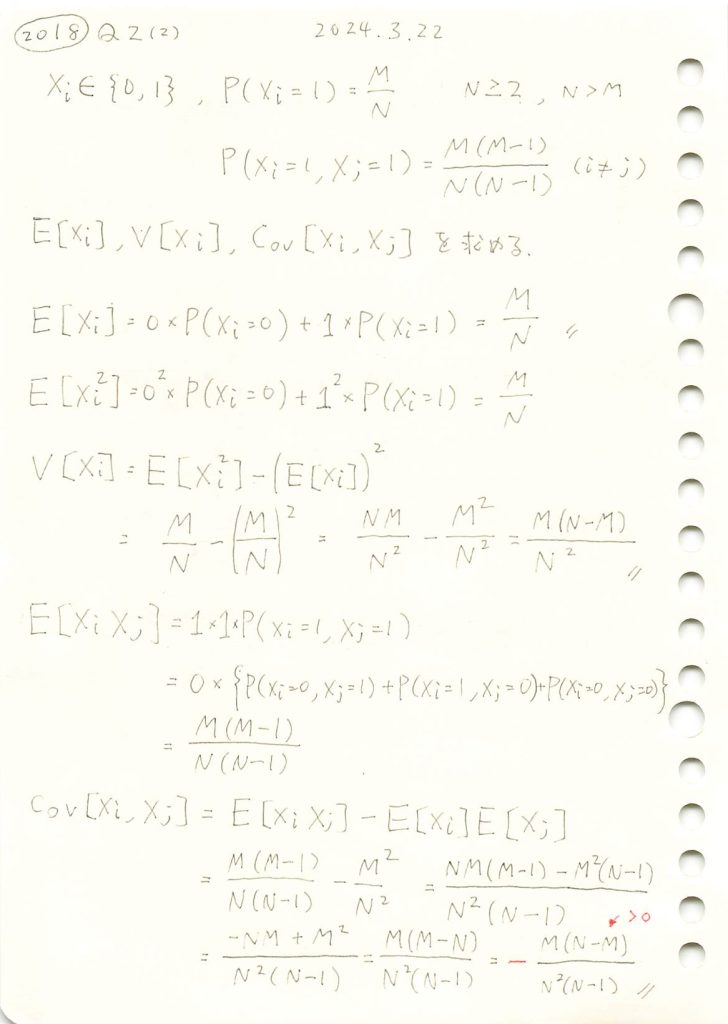
コード
NとMを変化させて期待値E[Xi]についてシミュレーションを行い理論値と一致するか確認します。
# 2018 Q2(2) 2024.10.6
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数
n_trials = 10000 # シミュレーションの試行回数
# 期待値 E[X_i] のグラフ描画
plt.figure(figsize=(10, 6))
for N in N_values:
M_values = np.arange(2, N + 1, M_steps) # 赤球数をステップで変化
# 理論値の計算
E_Xi_theory = M_values / N
# シミュレーションによる期待値の計算
E_Xi_simulation = []
for M in M_values:
count_Xi_1 = 0
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M)
drawn_ball = np.random.choice(balls, size=1, replace=False)
count_Xi_1 += drawn_ball[0]
E_Xi_simulation.append(count_Xi_1 / n_trials)
# グラフに追加描画
plt.plot(M_values, E_Xi_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, E_Xi_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
plt.xlabel('赤球の数 (M)')
plt.ylabel('期待値 E[X_i]')
plt.title('異なる N における 期待値 E[X_i] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()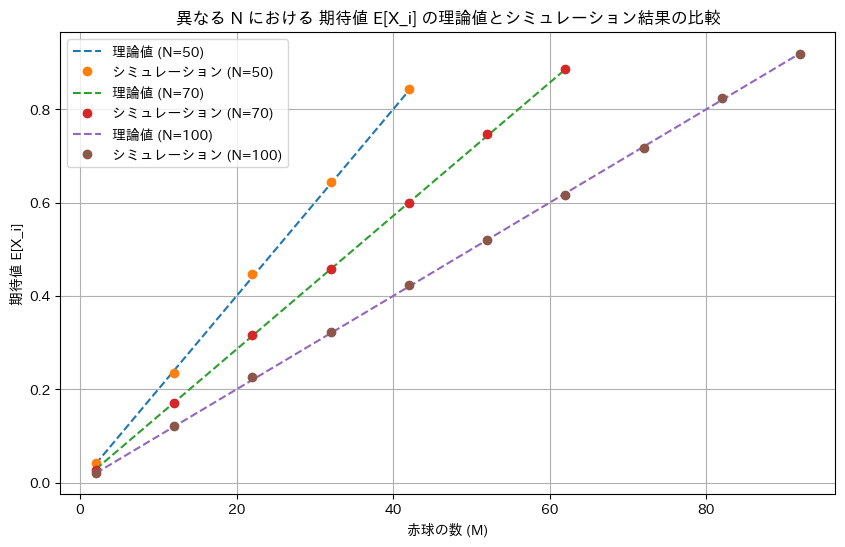
ミュレーションによる結果は理論値と一致しました。
次に、分散V[Xi]についてシミュレーションを行い理論値と一致するか確認します。
# 2018 Q2(2) 2024.10.6
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数
n_trials = 10000 # シミュレーションの試行回数
# 分散 V[X_i] のグラフ描画
plt.figure(figsize=(10, 6))
for N in N_values:
M_values = np.arange(2, N + 1, M_steps)
# 理論値の計算
V_Xi_theory = M_values * (N - M_values) / N**2
# シミュレーションによる分散の計算
V_Xi_simulation = []
for M in M_values:
Xi_values = []
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M)
drawn_ball = np.random.choice(balls, size=1, replace=False)
Xi_values.append(drawn_ball[0])
V_Xi_simulation.append(np.var(Xi_values))
# グラフに追加描画
plt.plot(M_values, V_Xi_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, V_Xi_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
plt.xlabel('赤球の数 (M)')
plt.ylabel('分散 V[X_i]')
plt.title('異なる N における 分散 V[X_i] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()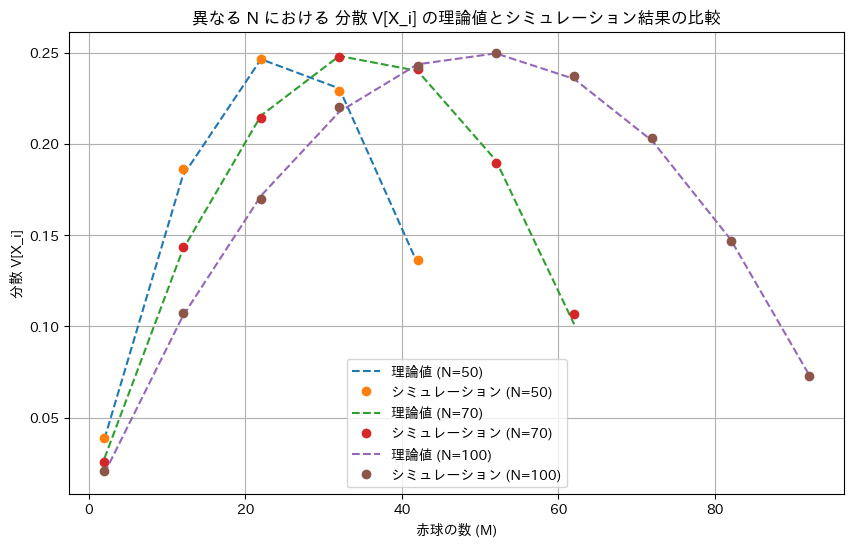
ミュレーションによる結果は理論値と一致しました。
次に、共分散Cov[Xi,Xj]についてシミュレーションを行い理論値と一致するか確認します。ただし、共分散は二変数を扱うため誤差が大きくなりやすいので、シミュレーションの試行回数を多め(1,000,000回)でやってみます。実行は環境により数十分かかることもあります。
# 2018 Q2(2) 2024.10.6
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数
n_trials = 1000000 # シミュレーションの試行回数
# 共分散 Cov[X_i, X_j] のグラフ描画
plt.figure(figsize=(10, 6))
for N in N_values:
M_values = np.arange(2, N + 1, M_steps)
# 理論値の計算
Cov_Xi_Xj_theory = -(M_values * (N - M_values)) / (N**2 * (N - 1))
# シミュレーションによる共分散の計算
Cov_Xi_Xj_simulation = []
for M in M_values:
Xi_values = []
Xj_values = []
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M)
drawn_balls = np.random.choice(balls, size=2, replace=False)
Xi_values.append(drawn_balls[0])
Xj_values.append(drawn_balls[1])
Cov_Xi_Xj_simulation.append(np.cov(Xi_values, Xj_values)[0, 1])
# グラフに追加描画
plt.plot(M_values, Cov_Xi_Xj_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, Cov_Xi_Xj_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
plt.xlabel('赤球の数 (M)')
plt.ylabel('共分散 Cov[X_i, X_j]')
plt.title('異なる N における 共分散 Cov[X_i, X_j] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()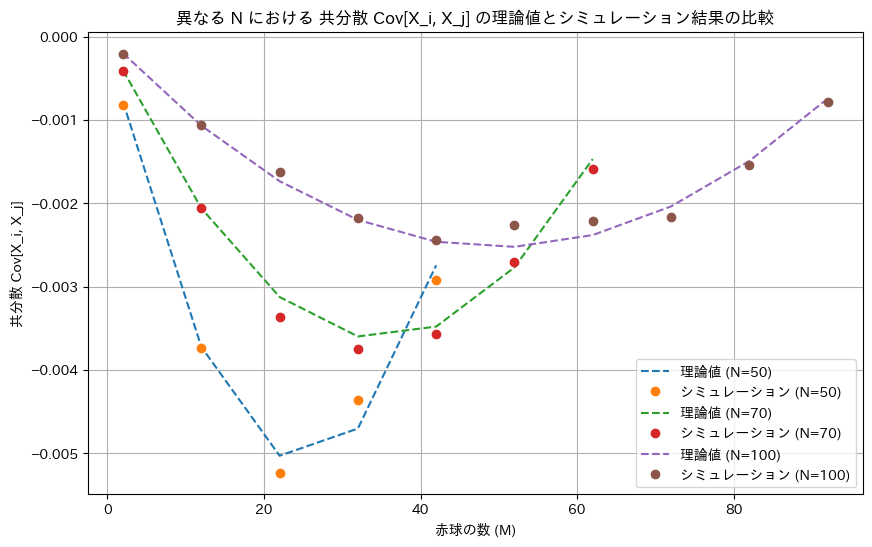
シミュレーションによる結果は概ね一致しました。
2018 Q2(1)-2
非復元無作為抽出でi番目とj番目が当たりになる確率を求めました。

コード
NとMを変化させてシミュレーションを行い理論値と一致するか確認します。
# 2018 Q2(1)-2 2024.10.5
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数を指定
n_trials = 10000 # シミュレーションの試行回数
# グラフ描画の準備
plt.figure(figsize=(10, 6))
# 各 N に対してシミュレーションと理論値を計算
for N in N_values:
M_values = np.arange(2, N + 1, M_steps) # 赤球数をステップで変化 (M >= 2 に設定)
# 理論値の計算
P_Xi_Xj_theory = (M_values / N) * ((M_values - 1) / (N - 1))
# シミュレーションによる確率計算
P_Xi_Xj_simulation = []
for M in M_values:
count_Xi_Xj_1 = 0
for _ in range(n_trials):
# 箱の中の球を準備(赤球 M 個、青球 N-M 個)
balls = [1] * M + [0] * (N - M)
# 非復元抽出で2つの球を無作為に抽出
drawn_balls = np.random.choice(balls, size=2, replace=False)
# 2回連続で赤球が引かれたか確認
if drawn_balls[0] == 1 and drawn_balls[1] == 1:
count_Xi_Xj_1 += 1
# シミュレーション結果の確率
P_Xi_Xj_simulation.append(count_Xi_Xj_1 / n_trials)
# グラフに追加描画
plt.plot(M_values, P_Xi_Xj_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, P_Xi_Xj_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
# グラフのラベルとタイトル設定
plt.xlabel('赤球の数 (M)')
plt.ylabel('P(X_i = 1, X_j = 1) の確率')
plt.title('異なる N における P(X_i = 1, X_j = 1) の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()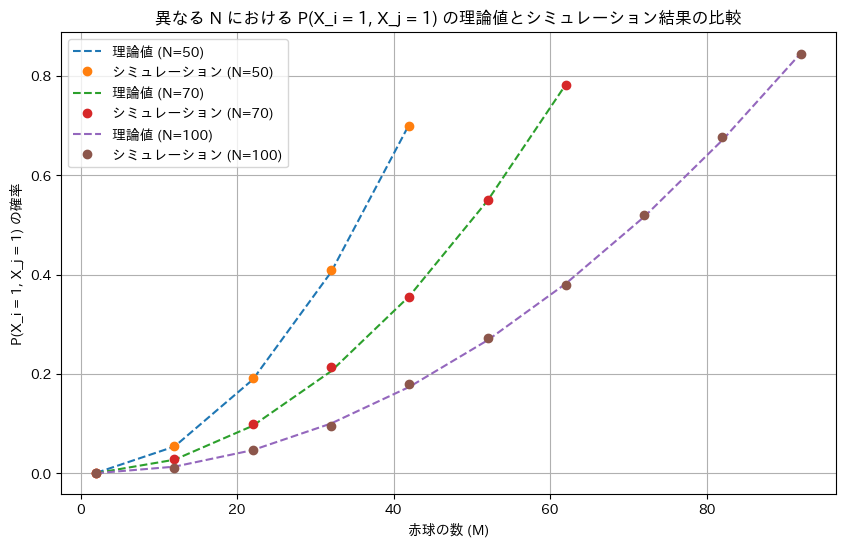
シミュレーションによる結果は理論値と一致しました。
2018 Q2(1)-1
非復元無作為抽出で当たりの出る確率を求めました。

コード
NとMを変化させてシミュレーションを行い理論値と一致するか確認します。
# 2018 Q2(1)-1 2024.10.5
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数を指定
n_trials = 10000 # シミュレーションの試行回数
# グラフ描画の準備
plt.figure(figsize=(10, 6))
# 各 N に対してシミュレーションと理論値を計算
for N in N_values:
M_values = np.arange(1, N + 1, M_steps) # 赤球数をステップで変化
P_Xi_1_theory = M_values / N # 理論値
# シミュレーションによる確率計算
P_Xi_1_simulation = []
for M in M_values:
count_Xi_1 = 0
for _ in range(n_trials):
# 箱の中の球を準備(赤球 M 個、青球 N-M 個)
balls = [1] * M + [0] * (N - M)
# 1回の無作為抽出で赤球が引かれるかどうかを確認
drawn_ball = np.random.choice(balls)
if drawn_ball == 1:
count_Xi_1 += 1
# シミュレーション結果の確率
P_Xi_1_simulation.append(count_Xi_1 / n_trials)
# グラフに追加描画
plt.plot(M_values, P_Xi_1_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, P_Xi_1_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
# グラフのラベルとタイトル設定
plt.xlabel('赤球の数 (M)')
plt.ylabel('P(X_i = 1) の確率')
plt.title('異なる N における理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()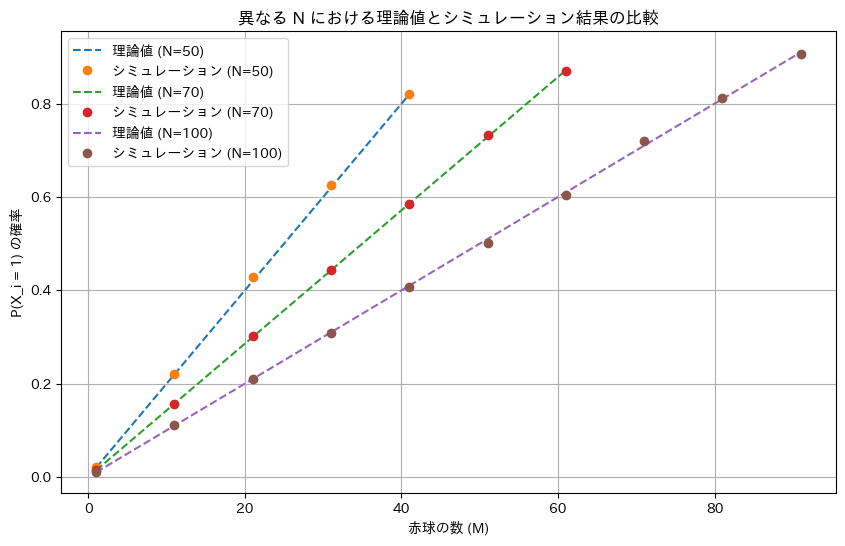
シミュレーションによる結果は理論値と一致しました。
2018 Q1(4)-2
(別解)不偏分散の平方根の期待値の母標準偏差に対する偏りを求めました。
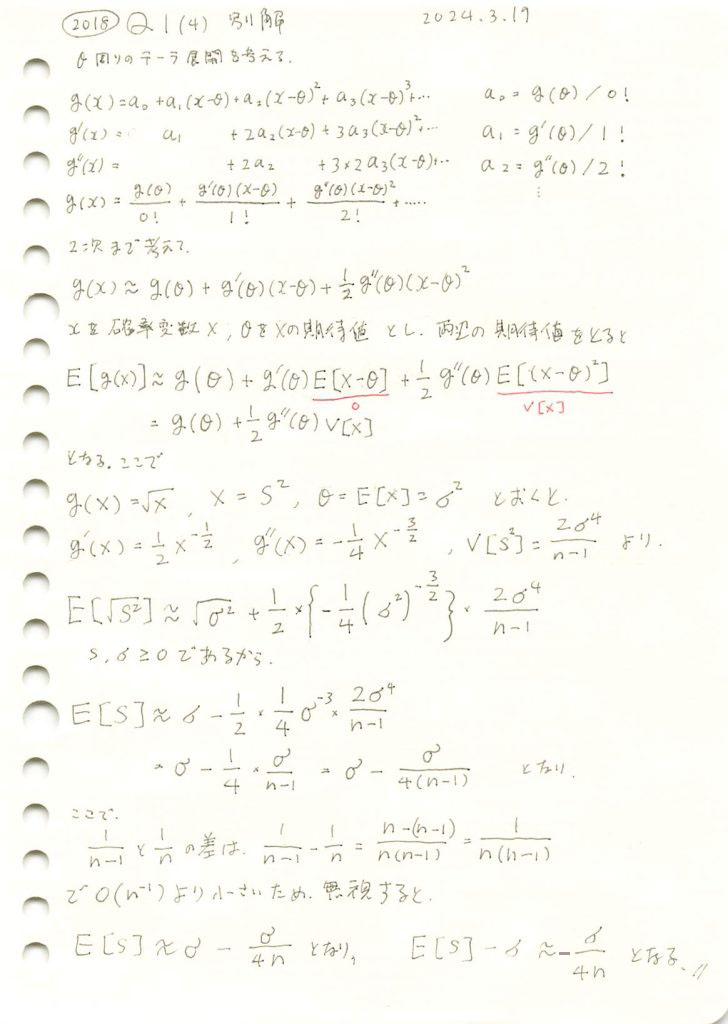
コード
数値シミュレーションでE[S] 求め、理論値![]() と一致するか確認します。
と一致するか確認します。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 2 # 母標準偏差
n_values = np.array([10, 20, 50, 100, 200]) # サンプルサイズの値
num_simulations = 10000 # シミュレーションの回数
# 結果を格納するリスト
simulated_means = []
theoretical_means = []
sigma_values = [sigma] * len(n_values) # 母標準偏差の値をリストで作成
# シミュレーション実行
for n in n_values:
# カイ二乗分布に従う乱数を生成
chi_squared_samples = np.random.chisquare(df=n-1, size=num_simulations)
# 標本標準偏差 S のシミュレーション
S_simulation = sigma * np.sqrt(chi_squared_samples / (n - 1))
# シミュレーションの期待値 (平均)
simulated_mean = np.mean(S_simulation)
simulated_means.append(simulated_mean)
# 理論値 E[S] = σ - σ / (4n)
theoretical_mean = sigma - sigma / (4 * n)
theoretical_means.append(theoretical_mean)
# 結果表示
for i, n in enumerate(n_values):
print(f"n = {n}: シミュレーション平均 = {simulated_means[i]:.4f}, 理論値 = {theoretical_means[i]:.4f}, 母標準偏差 = {sigma:.4f}")
# グラフ描画
plt.figure(figsize=(8, 6))
plt.plot(n_values, simulated_means, 'bo-', label='シミュレーション平均')
plt.plot(n_values, theoretical_means, 'r--', label='理論値')
plt.plot(n_values, sigma_values, 'g-', label='母標準偏差 σ')
plt.xlabel('サンプルサイズ n')
plt.ylabel('期待値 E[S]')
plt.title('標本標準偏差 E[S] のシミュレーションと理論値の比較')
plt.legend()
plt.grid(True)
plt.show()n = 10: シミュレーション平均 = 1.9394, 理論値 = 1.9500, 母標準偏差 = 2.0000
n = 20: シミュレーション平均 = 1.9747, 理論値 = 1.9750, 母標準偏差 = 2.0000
n = 50: シミュレーション平均 = 1.9888, 理論値 = 1.9900, 母標準偏差 = 2.0000
n = 100: シミュレーション平均 = 1.9961, 理論値 = 1.9950, 母標準偏差 = 2.0000
n = 200: シミュレーション平均 = 1.9974, 理論値 = 1.9975, 母標準偏差 = 2.0000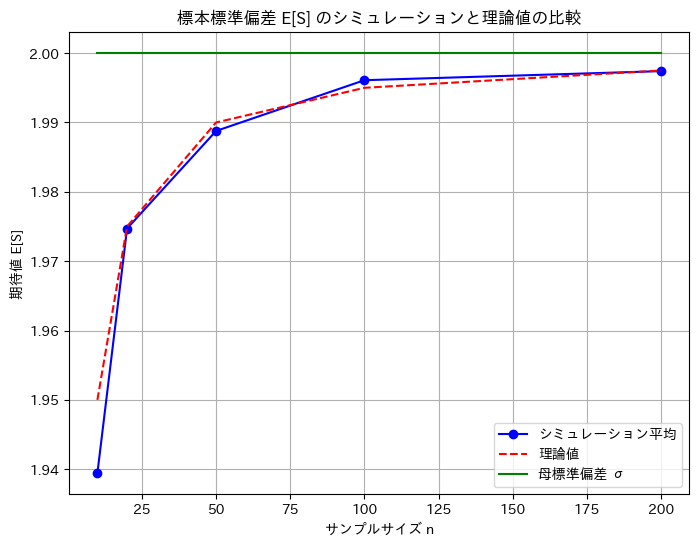
数値シミュレーションでのE[S]は、理論値![]() に一致することが確認できました。
に一致することが確認できました。