ホーム » 統計検定1級 2015年 統計数理 (ページ 3)
「統計検定1級 2015年 統計数理」カテゴリーアーカイブ
2015 Q2(1)
標本平均とP値の関係をグラフで描きました。

コード
n=10のときの標本平均![]() とP値の関係をグラフで示します。また
とP値の関係をグラフで示します。また![]() のP値を計算します。
のP値を計算します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 問題の設定
n = 10 # サンプルサイズ
mu_0 = 0 # 帰無仮説の平均
sigma = 1 # 分散1なので標準偏差は1
alpha = 0.05 # 有意水準
critical_value = norm.ppf(1 - alpha) # 上側確率100α%点
threshold = critical_value / np.sqrt(n) # 棄却域の閾値
# 標本平均の値
x_bar_values = np.linspace(0, 1, 100) # 標本平均の範囲
p_values = 1 - norm.cdf((x_bar_values - mu_0) * np.sqrt(n)) # P値を計算
# 指定された x̄ = 0.3, 0.6 の場合の P値
x_bar_special = [0.3, 0.6]
p_values_special = 1 - norm.cdf((np.array(x_bar_special) - mu_0) * np.sqrt(n))
# 結果出力
print("指定された標本平均 x̄ に対応する P値:")
for x, p in zip(x_bar_special, p_values_special):
print(f" 標本平均 x̄ = {x:.1f} の場合の P値: {p:.3f}")
# グラフの描画
plt.figure(figsize=(8, 5))
plt.plot(x_bar_values, p_values, label="P値の挙動", color="orange")
plt.axhline(y=alpha, color="red", linestyle="--", label=f"有意水準 α={alpha}")
plt.scatter(x_bar_special, p_values_special, color="blue", label="指定点 (0.3, 0.6)")
for x, p in zip(x_bar_special, p_values_special):
plt.text(x, p, f"({x:.1f}, {p:.3f})", fontsize=10, color="blue")
plt.xlabel("標本平均 $\\bar{x}$", fontsize=12)
plt.ylabel("P値", fontsize=12)
plt.title("P値の挙動 (標本平均 $\\bar{x}$ の範囲)", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()指定された標本平均 x̄ に対応する P値:
標本平均 x̄ = 0.3 の場合の P値: 0.171
標本平均 x̄ = 0.6 の場合の P値: 0.029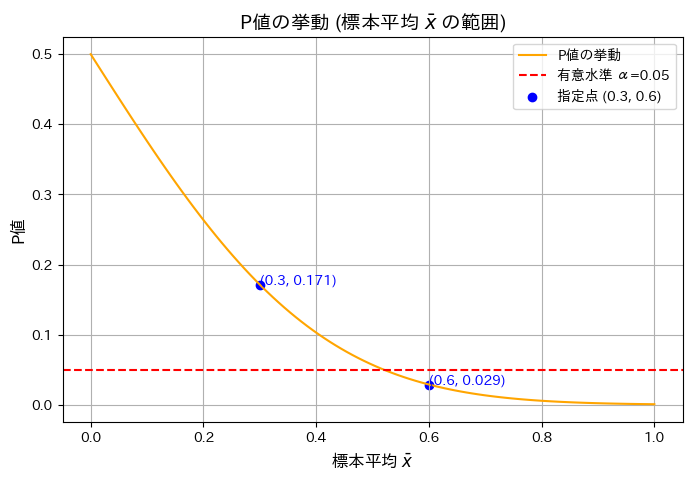
グラフの概形が描けました。標本平均![]() が大きくなるにつれてP値が減少することを確認しました。
が大きくなるにつれてP値が減少することを確認しました。
2015 Q1(5)
不偏分散の定数C倍を母分散の推定量とし平均二乗誤差を最小とするCを求めました。
コード
![]() を最小にするcが
を最小にするcが![]() であるか確認するため、シミュレーションを行います。n=20の場合において、c≒0.9がMSEの最小になることを検証します。
であるか確認するため、シミュレーションを行います。n=20の場合において、c≒0.9がMSEの最小になることを検証します。
# 2015 Q1(5) 2024.12.6
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma2 = 4 # 母分散
sigma = np.sqrt(sigma2) # 母標準偏差
n = 20 # 標本サイズ
num_simulations = 1000 # シミュレーション回数
# 理論値計算
c_theoretical = (n - 1) / (n + 1) # 理論的に最適な c
mse_theoretical_min = sigma2**2 * (2 / (n + 1)) # 最小 MSE の理論値
# シミュレーションで MSE を計算
c_values = np.linspace(0.5, 1.5, 100) # c をいろいろ変化させる
mse_simulated = []
for c in c_values:
simulated_errors = []
for _ in range(num_simulations):
sample = np.random.normal(0, sigma, n)
s2 = np.var(sample, ddof=1) # 不偏分散
error = (c * s2 - sigma2) ** 2 # 誤差の二乗
simulated_errors.append(error)
mse_simulated.append(np.mean(simulated_errors))
# グラフを描画
plt.figure(figsize=(10, 6))
plt.plot(c_values, mse_simulated, label="シミュレーションによる MSE", color='blue')
plt.axvline(c_theoretical, color='orange', linestyle='--', label=f"理論的な c={c_theoretical:.2f}")
plt.axhline(mse_theoretical_min, color='green', linestyle='--', label=f"最小理論 MSE={mse_theoretical_min:.2f}")
plt.title("MSE のシミュレーションと理論値")
plt.xlabel("c の値")
plt.ylabel("MSE")
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()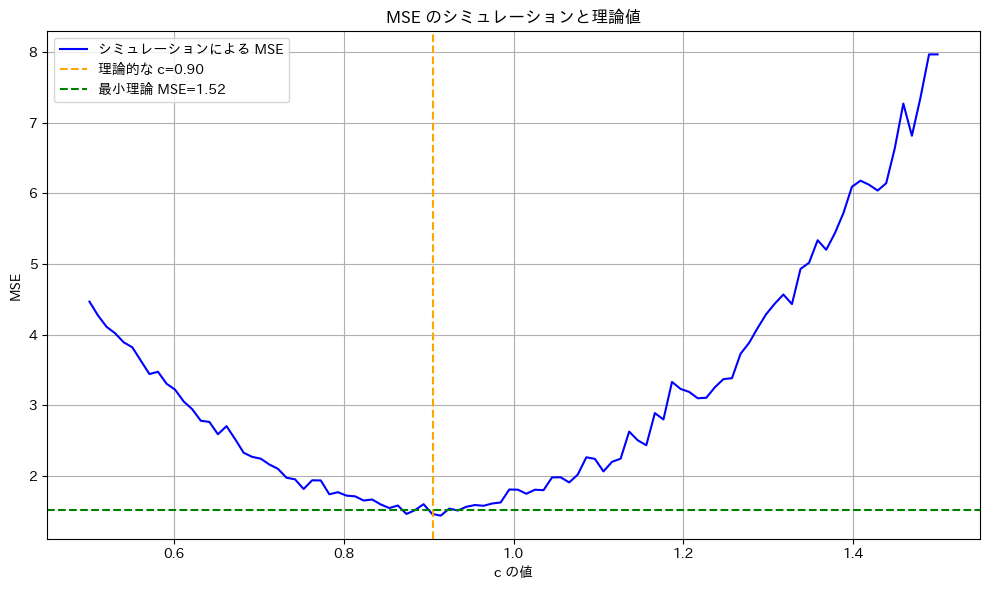
![]() は、n=20の場合において、理論通りc≒0.9のとき最小になることが確認されました。
は、n=20の場合において、理論通りc≒0.9のとき最小になることが確認されました。
2015 Q1(4)
不偏分散が母分散の一致推定量であることを確認しました。

コード
![]() が
が![]() の一致推定量であるか確認するため、
の一致推定量であるか確認するため、![]() をシミュレーションし、理論値とともにグラフで確認してみます。
をシミュレーションし、理論値とともにグラフで確認してみます。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
mu = 0 # 母平均
sigma2 = 4 # 母分散
sigma = np.sqrt(sigma2) # 母標準偏差
n_values = [10, 20, 50, 100, 200] # 標本サイズ
num_simulations = 1000 # シミュレーション回数
# 不偏分散の分散をシミュレーションで計算
simulated_variances = []
theoretical_variances = []
for n in n_values:
sample_variances = []
for _ in range(num_simulations):
sample = np.random.normal(mu, sigma, n)
unbiased_variance = np.var(sample, ddof=1) # 不偏分散
sample_variances.append(unbiased_variance)
# サンプル分散の分散を計算
var_of_sample_variance = np.var(sample_variances)
simulated_variances.append(var_of_sample_variance)
# 理論値を計算
theoretical_variance = 2 * sigma2**2 / (n - 1)
theoretical_variances.append(theoretical_variance)
# グラフの作成
plt.figure(figsize=(10, 6))
plt.plot(n_values, simulated_variances, marker='o', linestyle='-', color='blue', label="シミュレーション値")
plt.plot(n_values, theoretical_variances, marker='o', linestyle='--', color='orange', label="理論値")
# グラフの装飾
plt.title("不偏分散の分散の収束 (シミュレーション vs 理論)")
plt.xlabel("標本サイズ n")
plt.ylabel("分散 (Var[$S^2$])")
plt.grid()
plt.legend()
plt.tight_layout()
plt.show()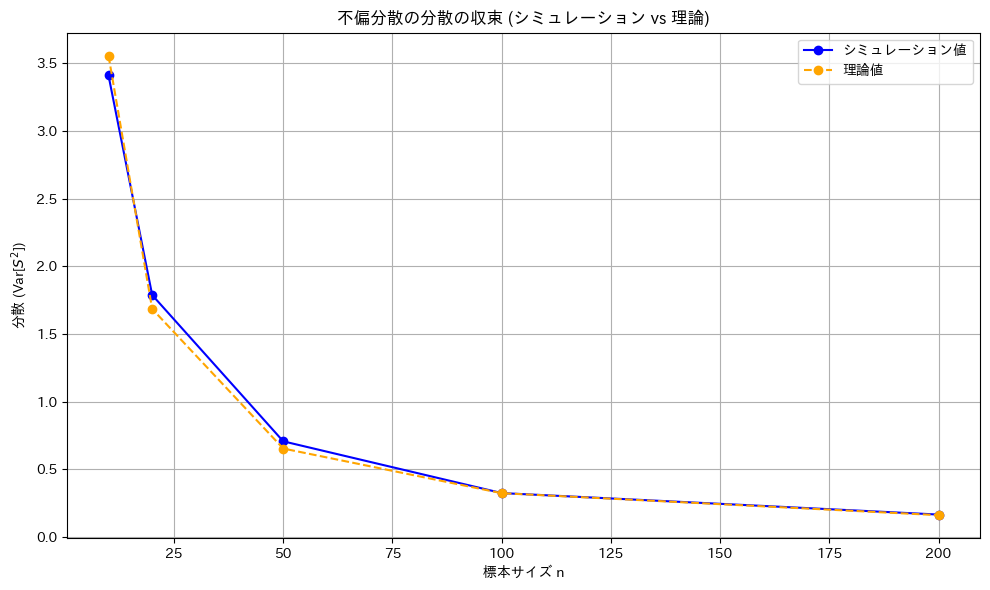
![]() のシミュレーション結果は、理論値
のシミュレーション結果は、理論値![]() とよく一致しました。また、nが増加すると分散が0に近づき、
とよく一致しました。また、nが増加すると分散が0に近づき、![]() が
が![]() の一致推定量であることが確認できました。
の一致推定量であることが確認できました。
2015 Q1(3)
平均周りの標本平均のk次モーメントを求めました。
コード
![]() の平均周りのk次モーメント
の平均周りのk次モーメント![]() を、kとnを変化させてグラフの形状を確認します。
を、kとnを変化させてグラフの形状を確認します。
# 2015 Q1(3) 2024.12.4
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gamma
# パラメータ設定
sigma2 = 4 # 母分散(固定)
k_values = [2, 4, 6, 8] # 偶数次モーメント
n_values = [12, 14, 16, 18, 20] # 標本サイズ
# 理論式計算の関数
def theoretical_moment_m(m, sigma2, n):
return (gamma(m + 0.5) / np.sqrt(np.pi)) * (2 * sigma2 / n) ** m
# グラフの準備
plt.figure(figsize=(10, 6))
# 各 n に対するモーメント値を計算してプロット
for n in n_values:
moment_values = [theoretical_moment_m(k // 2, sigma2, n) for k in k_values]
plt.plot(k_values, moment_values, marker='o', linestyle='-', label=f"n={n}")
# グラフ
#plt.title(r"モーメント $\frac{\Gamma(m + 1/2)}{\sqrt{\pi}} \left(\frac{2\sigma^2}{n}\right)^m$ の形状")
plt.title(r"$\overline{X}$ の平均周りの $k$ 次モーメントの形状")
plt.xlabel(r"$k$ (偶数次モーメントの次数)")
plt.ylabel("モーメント値")
plt.xticks(k_values)
plt.grid()
plt.legend()
plt.tight_layout()
plt.show()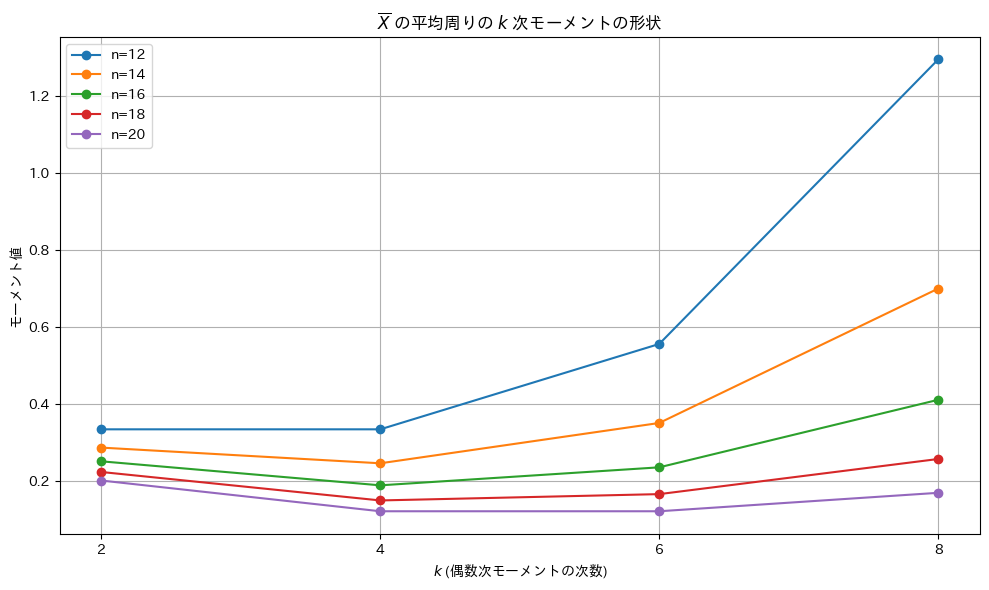
グラフの形状は谷型になっていることが確認され、特定の範囲でモーメント値が最小値を取ることがわかりました。
次に、シミュレーションを行います。標本サイズn=10の場合について実行し、理論値とシミュレーション結果が一致するかを確認します。
# 2015 Q1(3) 2024.12.4
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gamma
# パラメータ設定
mu = 0 # 母平均
sigma2 = 4 # 母分散
sigma = np.sqrt(sigma2) # 母標準偏差
n = 10 # 標本サイズ
k_values = [2, 4, 6, 8] # 偶数次モーメントを検証
num_simulations = 10000 # シミュレーション回数
# 理論値計算の関数
def theoretical_moment(k, sigma2, n):
m = k // 2
return (gamma(m + 0.5) / np.sqrt(np.pi)) * (2 * sigma2 / n) ** m
# シミュレーション値と理論値を計算
sim_results = []
theory_results = []
for k in k_values:
# シミュレーションで k 次モーメントを計算
sample_means = [np.mean(np.random.normal(mu, sigma, n)) for _ in range(num_simulations)]
k_moment_sim = np.mean([(x - mu) ** k for x in sample_means])
# 理論値を計算
k_moment_theory = theoretical_moment(k, sigma2, n)
# 保存
sim_results.append(k_moment_sim)
theory_results.append(k_moment_theory)
# 棒グラフを作成
x = np.arange(len(k_values))
width = 0.4
plt.figure(figsize=(10, 6))
# プロット
plt.bar(x - width / 2, sim_results, width, label="シミュレーション値", color='blue', alpha=0.7)
plt.bar(x + width / 2, theory_results, width, label="理論値", color='orange', alpha=0.7)
# 軸とラベル
plt.xticks(x, [f"k={k}" for k in k_values])
plt.title(f"標本サイズ n={n} におけるモーメント比較")
plt.xlabel("k 次モーメント")
plt.ylabel("モーメント値")
plt.legend()
plt.grid(axis='y')
# 表示
plt.tight_layout()
plt.show()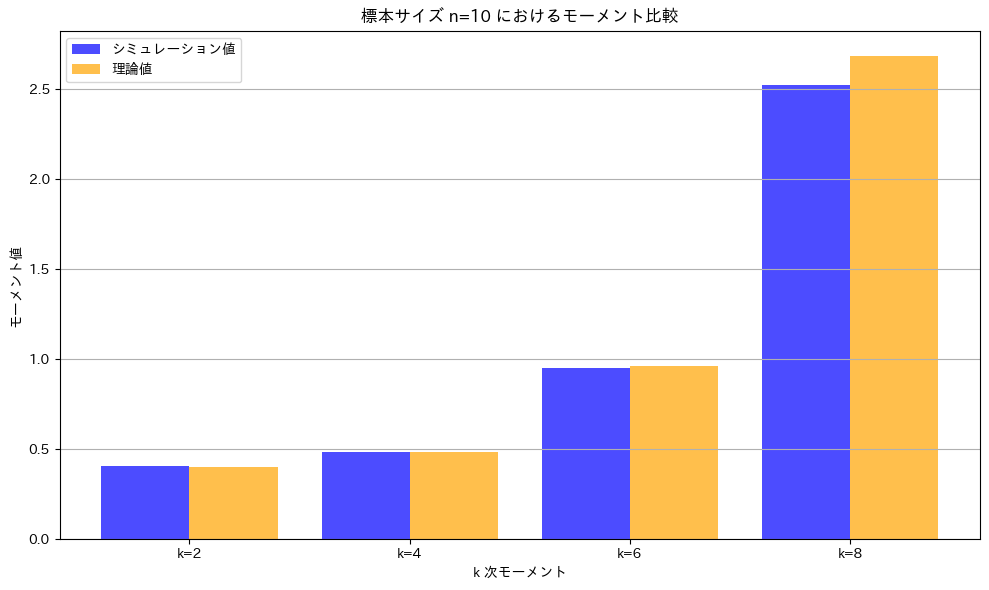
理論値とシミュレーションによる値はよく一致しています。
n=20でもう一度実行します。
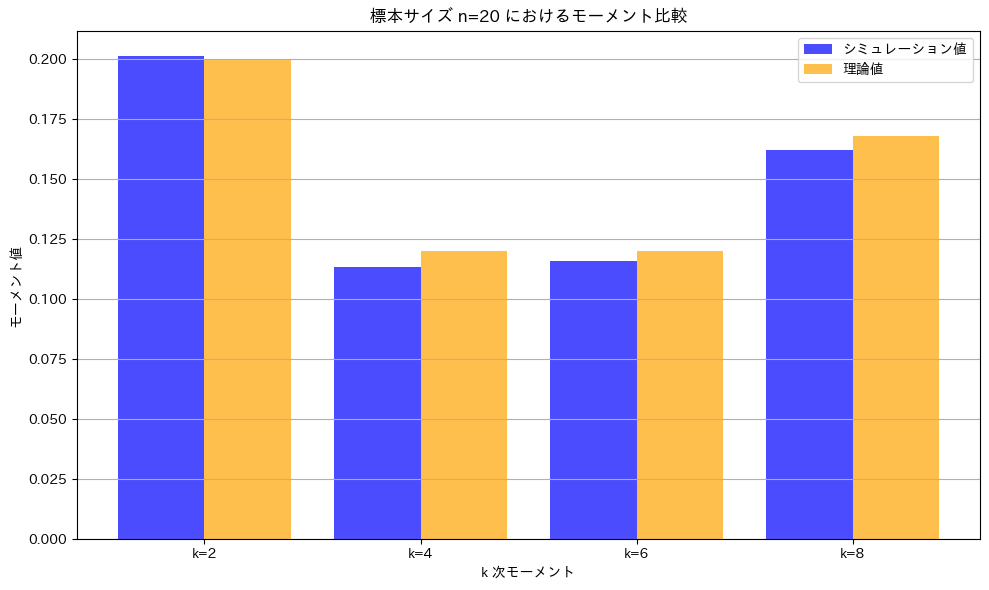
こちらもよく一致しています。グラフの形状が谷型になっていることも確認できました。
2015 Q1(2)
不偏分散が母分散の不偏推定量である事を示しました。
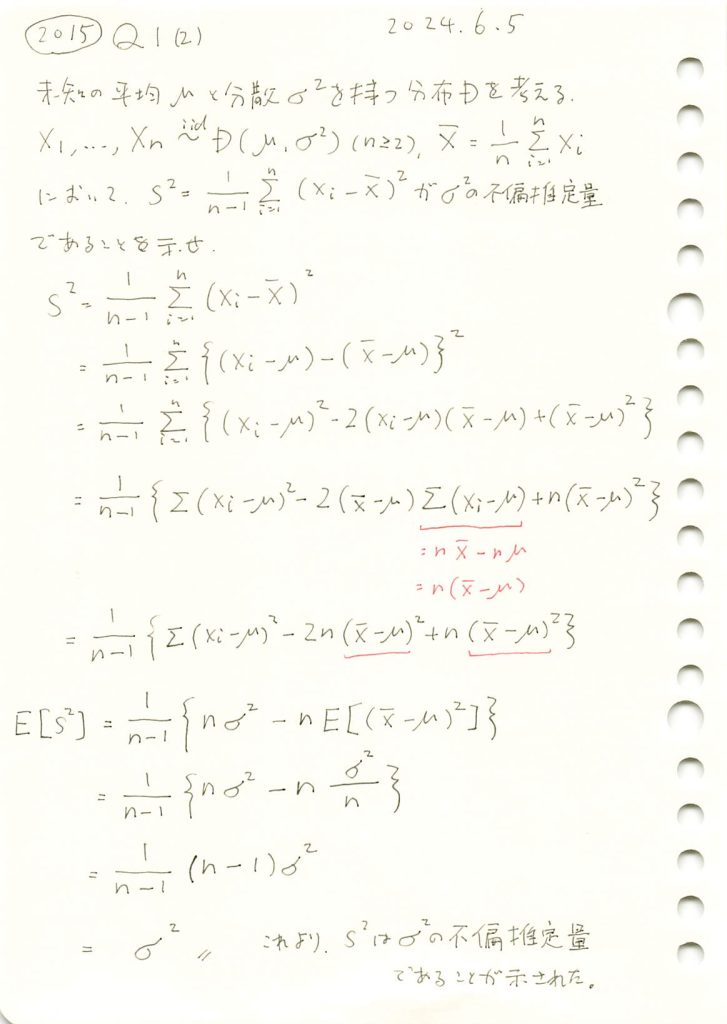
コード
※2018 Q1(1)から引用https://statistics.blue/2018-q11/
nを2~100に変化させて、不偏分散と標本分散を比較してみます。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
mu = 0 # 母集団平均
sigma = 2 # 母集団標準偏差
sigma_squared = sigma ** 2 # 真の母分散
n_values = range(2, 101, 2) # サンプルサイズ n を2から100まで2ステップで変化させる
num_trials = 3000 # 各 n に対して100回の試行を行う
# 不偏分散 (1/(n-1)) と 標本分散 (1/n) を計算するためのリスト
unbiased_variances = []
biased_variances = []
# 各サンプルサイズ n で分散を計算
for n in n_values:
unbiased_variance_sum = 0
biased_variance_sum = 0
# 各サンプルサイズ n に対して複数回試行して平均を計算
for _ in range(num_trials):
# 正規分布に従うサンプルを生成
sample = np.random.normal(mu, sigma, n)
# 標本平均
sample_mean = np.mean(sample)
# 不偏分散 (1/(n-1))
unbiased_variance = np.sum((sample - sample_mean) ** 2) / (n - 1)
unbiased_variance_sum += unbiased_variance
# 標本分散 (1/n)
biased_variance = np.sum((sample - sample_mean) ** 2) / n
biased_variance_sum += biased_variance
# 各 n に対する平均分散をリストに追加
unbiased_variances.append(unbiased_variance_sum / num_trials)
biased_variances.append(biased_variance_sum / num_trials)
# グラフを描画
plt.plot(n_values, unbiased_variances, label="不偏分散 (1/(n-1))", color='blue', marker='o')
plt.plot(n_values, biased_variances, label="標本分散 (1/n)", color='red', linestyle='--', marker='x')
# 真の分散を水平線で描画
plt.axhline(y=sigma_squared, color='green', linestyle='-', label=f'真の分散 = {sigma_squared}')
# グラフの設定
plt.title('サンプルサイズに対する標本分散と不偏分散の比較')
plt.xlabel('サンプルサイズ n')
plt.ylabel('分散')
plt.legend()
plt.grid(True)
plt.show()
標本分散には不偏性はなく、不偏分散には不偏性があることが確認できました。
次に、![]() と
と![]() を棒グラフで比較してみます。
を棒グラフで比較してみます。
# 2015 Q1(2) 2024.12.3
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
mu = 0 # 母平均
sigma = 2 # 母標準偏差
n = 10 # 標本サイズ
num_simulations = 30 # シミュレーション回数
# 共通のシミュレーションサンプルを生成
samples = [np.random.normal(mu, sigma, n) for _ in range(num_simulations)]
# 各シミュレーションで E[(X - X̄)^2] と E[(X - μ)^2] を計算
var_sample_mean = [np.mean((sample - np.mean(sample))**2) for sample in samples] # E[(X - X̄)^2]
var_population_mean = [np.mean((sample - mu)**2) for sample in samples] # E[(X - μ)^2]
# 棒グラフの準備
x = np.arange(1, num_simulations + 1) # シミュレーション番号
plt.figure(figsize=(12, 6))
# 棒グラフをプロット
plt.bar(x - 0.2, var_sample_mean, width=0.4, label=r"$E[(X - \overline{X})^2]$", color='blue', alpha=0.7)
plt.bar(x + 0.2, var_population_mean, width=0.4, label=r"$E[(X - \mu)^2]$", color='orange', alpha=0.7)
# グラフ
plt.title(r"$E[(X - \overline{X})^2]$ と $E[(X - \mu)^2]$ の比較")
plt.xlabel("シミュレーション番号")
plt.ylabel("値")
plt.xticks(x) # シミュレーション番号をx軸に設定
plt.legend()
plt.grid(axis='y')
# 表示
plt.tight_layout()
plt.show()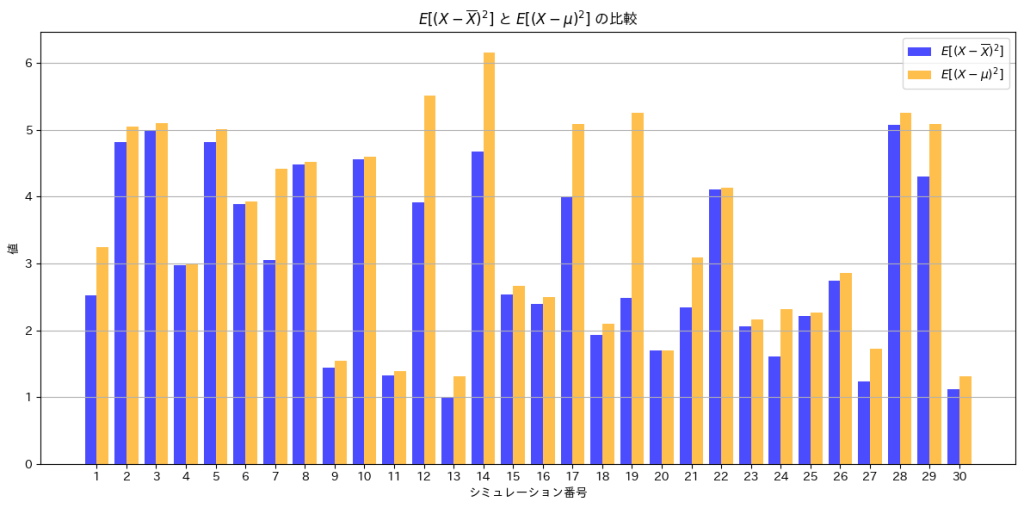
![]() は、
は、![]() よりも小さくなっていることが分かります。不偏分散
よりも小さくなっていることが分かります。不偏分散![]() は、nでなくn-1で割ることで、母分散の推定値として偏りを修正しています。
は、nでなくn-1で割ることで、母分散の推定値として偏りを修正しています。
2015 Q1(1)
任意の分布に従う確率変数の平均の二乗の期待値を求めました。
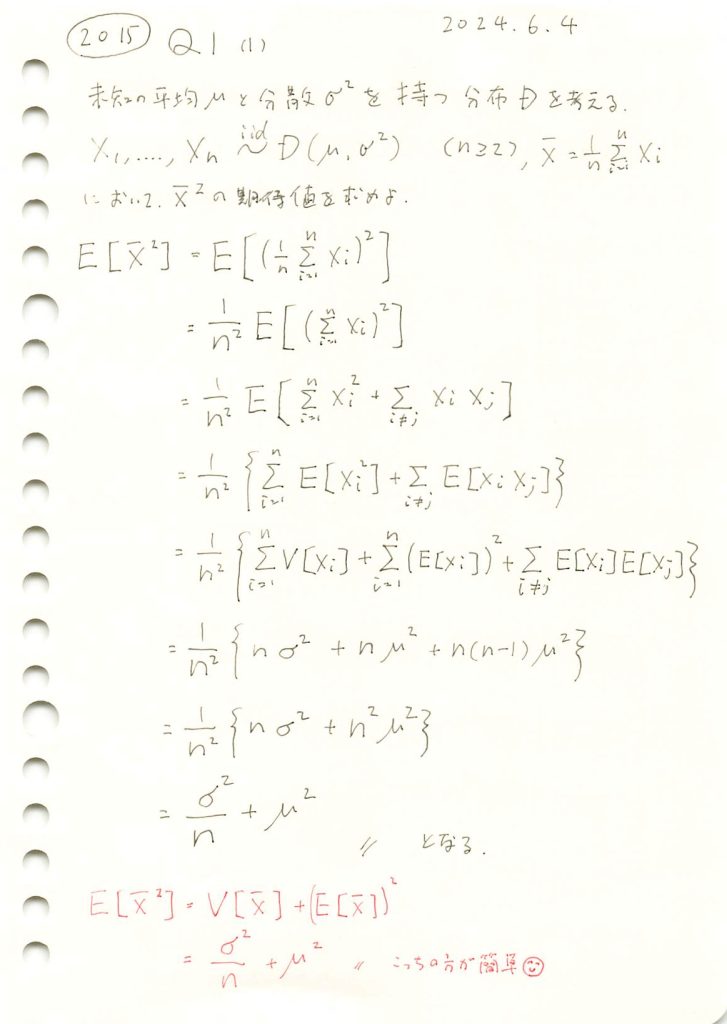
コード
![]() を確かめるためにシミュレーションを行います。nを変化させながら乱数を発生させ、計算した
を確かめるためにシミュレーションを行います。nを変化させながら乱数を発生させ、計算した![]() を理論値(非心カイ二乗分布)と比較し、プロットしてみます。
を理論値(非心カイ二乗分布)と比較し、プロットしてみます。
#2015 Q1(1) 2024.12.2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import ncx2
# パラメータ設定(nを複数用意)
n_values = [5, 10, 20, 50] # 標本サイズのリスト
mu = 4 # 母平均
sigma2 = 5 # 母分散
sigma = np.sqrt(sigma2) # 母標準偏差
num_simulations = 10000 # シミュレーション回数
# 暖色系カラーパレットの設定
colors = plt.cm.autumn(np.linspace(0, 1, len(n_values)))
# 描画の準備
plt.figure(figsize=(10, 8))
# 結果格納用
results = []
# nごとに分布をシミュレーションし、プロット
for i, n in enumerate(n_values):
# シミュレーションによる標本平均の二乗 (X̄^2) の生成
sample_means_squared = np.array([
np.mean(np.random.normal(mu, sigma, n))**2 for _ in range(num_simulations)
])
# シミュレーションによる期待値 E[X̄^2] の計算
simulated_mean = np.mean(sample_means_squared)
# 理論値の計算
theoretical_mean = sigma2 / n + mu**2
# 結果を記録
results.append((n, theoretical_mean, simulated_mean))
# ヒストグラムをプロット
plt.hist(
sample_means_squared, bins=30, density=True, alpha=0.5,
label=f"n={n}, 理論値: {theoretical_mean:.3f}, シミュレーション値: {simulated_mean:.3f}",
color=colors[i]
)
# 非心カイ二乗分布のPDFをプロット
x_values = np.linspace(0, np.max(sample_means_squared), 1000)
df = 1 # 自由度は標本平均の二乗の場合、1となる
nc = (n * mu**2) / sigma2 # 非心度 λ
theoretical_pdf = ncx2.pdf(x_values, df, nc, scale=sigma2 / n)
plt.plot(
x_values, theoretical_pdf, linewidth=2, label=f"n={n} の非心カイ二乗分布", color=colors[i]
)
# グラフ
plt.title("標本平均の二乗 ($\\overline{X}^2$) の分布と非心カイ二乗分布")
plt.xlabel("$\\overline{X}^2$")
plt.ylabel("密度")
plt.legend()
plt.grid()
plt.show()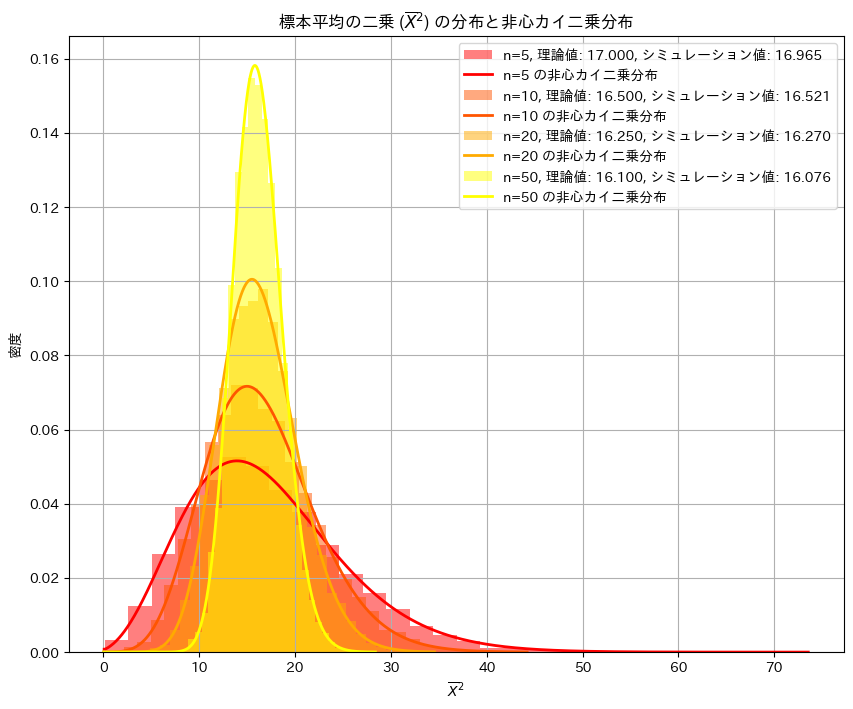
シミュレーションの結果、![]() と
と![]() は概ね一致しました。また
は概ね一致しました。また![]() の分布は理論値(非心カイ二乗分布)の形状とよく重なっていることが確認できました。
の分布は理論値(非心カイ二乗分布)の形状とよく重なっていることが確認できました。