ホーム » 統計検定1級 2014年 統計数理 (ページ 3)

「統計検定1級 2014年 統計数理」カテゴリーアーカイブ

投稿一覧

2014 Q1(2)

投稿日:2024年7月2日 　最終更新日:2024年12月29日

一様分布の指数を取る三つの確率変数のうち特定の一つが最大値をとる確率を求めました。

　

コード

与式はP(X = \max(X, Y, Z)) = P(X > \max(Y, Z))と考え、\alpha=2, \quad \beta=3, \quad \gamma=4とした場合のP(X > \max(Y, Z))をシミュレーションで計算し、理論値と比較します。

# 2014 Q1(2)  2024.12.29

import numpy as np
import matplotlib.pyplot as plt

# シミュレーションの設定
n_simulations = 10**6

# 一様分布からサンプリング
U = np.random.uniform(0, 1, n_simulations)
V = np.random.uniform(0, 1, n_simulations)
W = np.random.uniform(0, 1, n_simulations)

# パラメータの設定
alpha, beta, gamma = 2, 3, 4

# X, Y, Z の計算
X = U**alpha
Y = V**beta
Z = W**gamma

# 確率変数 Z を計算 (例: Z = X - max(Y, Z))
Z_diff = X - np.maximum(Y, Z)

# Z の累積分布関数 (CDF) を計算
z_sorted = np.sort(Z_diff)
cdf_Z = np.arange(1, len(z_sorted) + 1) / len(z_sorted)

# Z = 0 の累積確率を計算
cumulative_prob_at_zero = cdf_Z[np.searchsorted(z_sorted, 0)]

# 理論値の計算
theoretical_prob = (1 / alpha) / (1 / alpha + 1 / beta + 1 / gamma)

# 結果を出力
print(f"Z = 0 における累積確率: {cumulative_prob_at_zero:.3f}")
print(f"シミュレーション結果: P(X > max(Y, Z)) = {1 - cumulative_prob_at_zero:.6f}")
print(f"理論値: P(X > max(Y, Z)) = {theoretical_prob:.6f}")
print(f"誤差: {abs((1 - cumulative_prob_at_zero) - theoretical_prob):.6f}")

# PDF および CDF のプロット (PDF にも Z = 0 の赤い線を追加)
plt.figure(figsize=(14, 6))

# PDF
plt.subplot(1, 2, 1)
plt.hist(Z_diff, bins=100, density=True, alpha=0.7, label=r'$Z = X - \max(Y, Z)$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)')  # Z = 0 の赤い線を追加
plt.title('Z = X - max(Y, Z) の確率密度関数 (PDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()

# CDF
plt.subplot(1, 2, 2)
plt.plot(z_sorted, cdf_Z, label=r'$Z = X - \max(Y, Z)$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)')  # Z = 0 の赤い線
plt.text(0.05, cumulative_prob_at_zero, f'{cumulative_prob_at_zero:.3f}', color='red', fontsize=12)
plt.title('Z = X - max(Y, Z) の累積分布関数 (CDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('累積確率', fontsize=12)
plt.legend()

plt.tight_layout()
plt.show()
Z = 0 における累積確率: 0.538
シミュレーション結果: P(X > max(Y, Z)) = 0.462111
理論値: P(X > max(Y, Z)) = 0.461538
誤差: 0.000573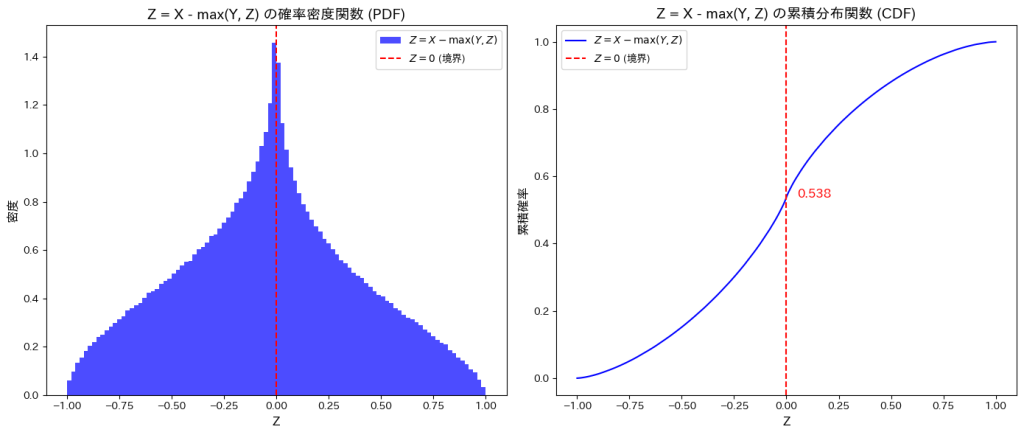

P(X > \max(Y, Z))はシミュレーションの結果、理論値と一致しました。

2014 Q1(1)

投稿日:2024年7月1日 　最終更新日:2024年12月28日

一様分布の指数を取る二つの確率変数の大小が決まっている場合の確率を条件付確率の期待値を取ることで求めました。

　

コード

XとYの頻度分布を3Dプロットで可視化してみます。

# 2014 Q1(1)  2024.12.28

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# シミュレーションの設定
n_simulations = 10**5  # サンプルサイズ

# 一様分布からサンプリング
U = np.random.uniform(0, 1, n_simulations)
V = np.random.uniform(0, 1, n_simulations)

# X, Y の計算
X = U**2
Y = V**3

# 3Dプロット
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 2次元ヒストグラムを計算
hist, xedges, yedges = np.histogram2d(X, Y, bins=50, density=True)

# 座標軸を作成
xpos, ypos = np.meshgrid(xedges[:-1], yedges[:-1], indexing="ij")
xpos = xpos.ravel()
ypos = ypos.ravel()
zpos = np.zeros_like(xpos)

# 棒の高さ
dx = dy = 0.02
dz = hist.ravel()

# 色分け: X > Y (緑), X = Y (黄色), X < Y (青)
tolerance = 0.01  # 許容範囲を指定して X = Y の近似を表現
colors = np.where(
    np.abs(xpos - ypos) < tolerance, 'yellow',
    np.where(xpos > ypos, 'green', 'blue')
)

# 3Dバーを描画
ax.bar3d(xpos, ypos, zpos, dx, dy, dz, zsort='average', alpha=0.7, color=colors)

# ラベルとタイトル
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('頻度', labelpad=-10)  # ラベルの位置を調整
#ax.set_title(r'$X > Y$ (緑), $X = Y$ (黄色), $X < Y$ (青)', fontsize=14)
#ax.set_title(r'$X$ と $Y$ の出現頻度', fontsize=14)
ax.set_title(r'$X$ と $Y$ の出現頻度（組）', fontsize=14)

# 凡例
legend_handles = [
    plt.Line2D([0], [0], color='green', lw=4, label=r'$X > Y$ (緑)'),
    plt.Line2D([0], [0], color='yellow', lw=4, label=r'$X = Y$ (黄色)'),
    plt.Line2D([0], [0], color='blue', lw=4, label=r'$X < Y$ (青)')
]
ax.legend(handles=legend_handles, loc='upper left', bbox_to_anchor=(1.05, 1), fontsize=10)

# カメラビュー
ax.view_init(elev=30, azim=45)

plt.tight_layout()
plt.show()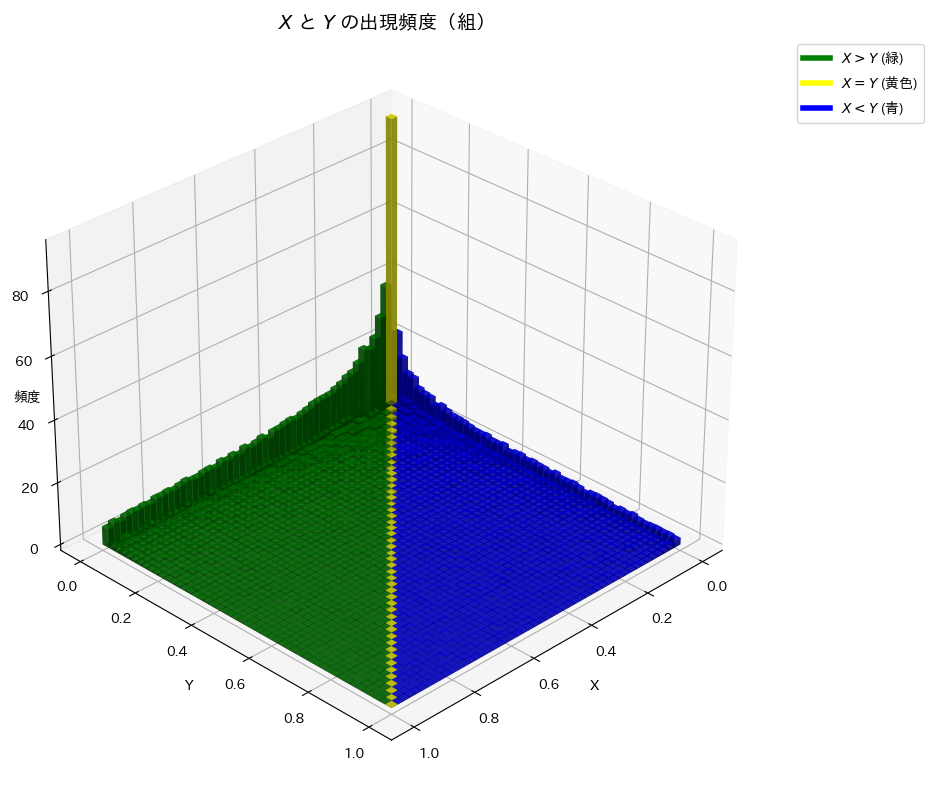

X>Yの領域は、X<Yの領域と比べて出現頻度が高いようです。

次に、XとYの大小関係を確認するために確率変数Z=X-Yを同に導入し、その確率密度と累積分布をシミュレーションにより求め、P(X>Y)を計算してみます。

# 2014 Q1(1)  2024.12.28

import numpy as np
import matplotlib.pyplot as plt

# シミュレーションの設定
np.random.seed(42)
n_simulations = 10**6

# 一様分布からサンプリング
U = np.random.uniform(0, 1, n_simulations)
V = np.random.uniform(0, 1, n_simulations)

# X, Y の計算
X = U**2
Y = V**3

# Z = X - Y を計算
Z = X - Y

# Z の累積分布関数 (CDF) を計算
z_sorted = np.sort(Z)
cdf_Z = np.arange(1, len(z_sorted) + 1) / len(z_sorted)

# Z = 0 の累積確率を計算
cumulative_prob_at_zero = cdf_Z[np.searchsorted(z_sorted, 0)]

# 結果を出力
print(f"Z = 0 における累積確率: {cumulative_prob_at_zero:.3f}")
print(f"P(X > Y) = {1 - cumulative_prob_at_zero:.3f}")

# PDF および CDF のプロット (PDF にも Z = 0 の赤い線を追加)
plt.figure(figsize=(14, 6))

# PDF
plt.subplot(1, 2, 1)
plt.hist(Z, bins=100, density=True, alpha=0.7, label=r'$Z = X - Y$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)')  # Z = 0 の赤い線を追加
plt.title('Z = X - Y の確率密度関数 (PDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()

# CDF
plt.subplot(1, 2, 2)
plt.plot(z_sorted, cdf_Z, label=r'$Z = X - Y$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)')  # Z = 0 の赤い線
plt.text(0.05, cumulative_prob_at_zero, f'{cumulative_prob_at_zero:.3f}', color='red', fontsize=12)
plt.title('Z = X - Y の累積分布関数 (CDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('累積確率', fontsize=12)
plt.legend()

plt.tight_layout()
plt.show()
Z = 0 における累積確率: 0.399
P(X > Y) = 0.601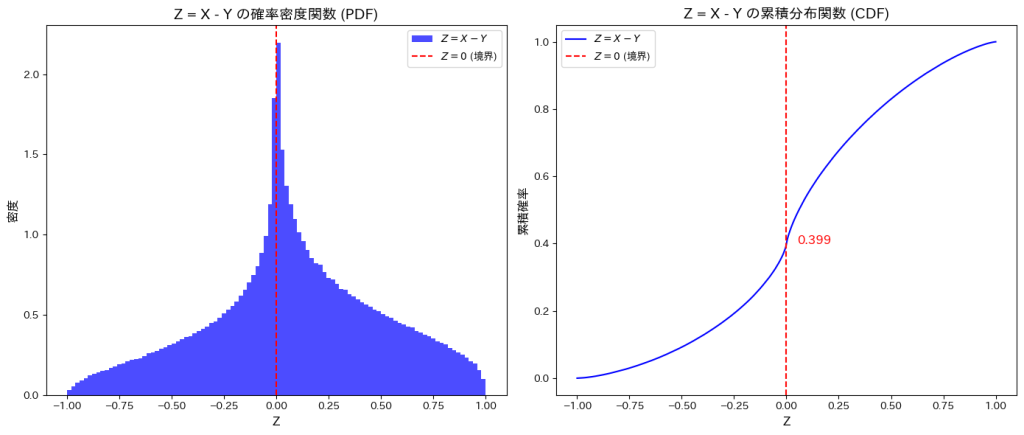

シミュレーションにより求めたP(X>Y)は、理論値と一致することが確認できました。

投稿ナビゲーション

新しい投稿 →