ホーム » 復習3周目 (ページ 10)
「復習3周目」カテゴリーアーカイブ
2017 Q1(1)
不偏分散が母分散の不偏推定量であることを示しました。
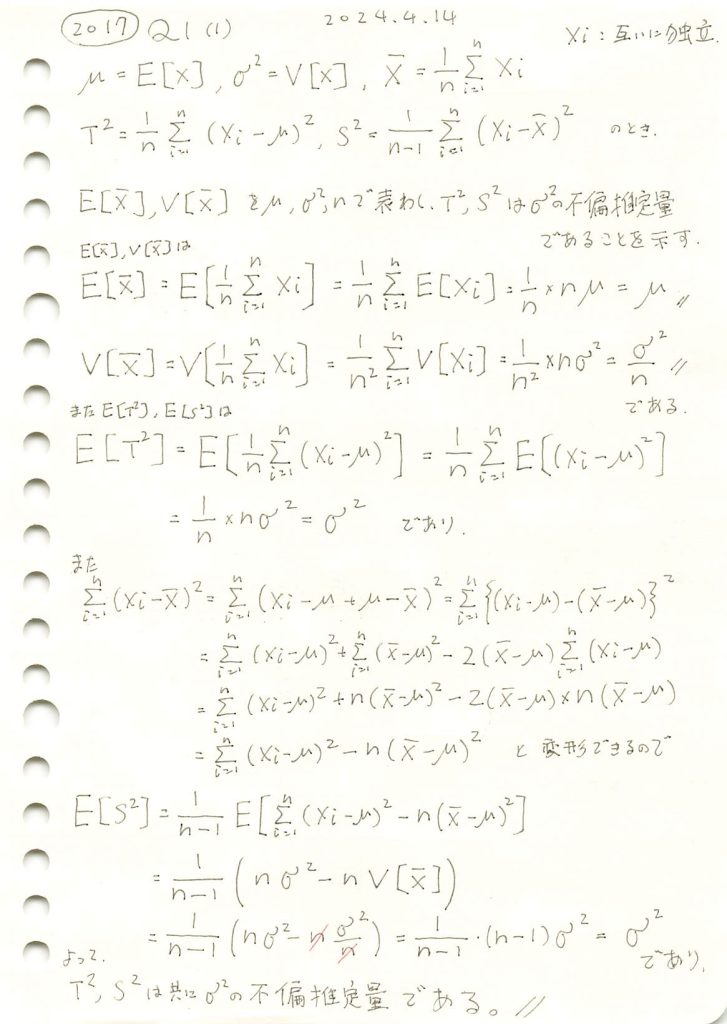
コード
サンプルサイズnを変化させて![]() ,
,![]() ,
,![]() ,
,![]() をそれぞれシミュレーションして描画します。
をそれぞれシミュレーションして描画します。
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータの設定
mu = 5.0 # 母平均
sigma = 2.0 # 母標準偏差
num_simulations = 1000 # シミュレーションの繰り返し回数
# n の範囲を設定 (100 から 10000 まで 100 刻み)
n_values = range(100, 10100, 100)
# 各 n に対する統計量を保存するリスト
E_X_bar_list = []
V_X_bar_list = []
E_T2_list = []
E_S2_list = []
# 各 n に対するシミュレーションの実行
for n in n_values:
sample_means = []
T2_values = []
S2_values = []
# シミュレーションの実行
for _ in range(num_simulations):
sample = np.random.normal(mu, sigma, n)
sample_mean = np.mean(sample)
sample_means.append(sample_mean)
# T^2 計算 (母平均使用)
T2 = np.mean((sample - mu) ** 2)
T2_values.append(T2)
# S^2 計算 (標本平均使用)
S2 = np.var(sample, ddof=1)
S2_values.append(S2)
# 結果をリストに保存
E_X_bar_list.append(np.mean(sample_means))
V_X_bar_list.append(np.var(sample_means))
E_T2_list.append(np.mean(T2_values))
E_S2_list.append(np.mean(S2_values))
# グラフの作成(理論値を追加)
plt.figure(figsize=(14, 10))
# 理論値
theoretical_mean = mu # E[X_bar] の理論値
theoretical_variance = sigma**2 / np.array(n_values) # V[X_bar] の理論値
theoretical_variance_true = sigma**2 # 母分散
# E[X_bar] のプロット
plt.subplot(2, 2, 1)
plt.plot(n_values, E_X_bar_list, marker='o', label='シミュレーション')
plt.axhline(y=theoretical_mean, color='r', linestyle='--', label='理論値: $E[\overline{X}] = \mu$')
plt.title('$E[\overline{X}]$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$E[\overline{X}]$')
plt.legend()
# V[X_bar] のプロット
plt.subplot(2, 2, 2)
plt.plot(n_values, V_X_bar_list, marker='o', label='シミュレーション')
plt.plot(n_values, theoretical_variance, color='r', linestyle='--', label='理論値: $V[\overline{X}] = \\frac{\sigma^2}{n}$')
plt.title('$V[\overline{X}]$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$V[\overline{X}]$')
plt.legend()
# E[T^2] のプロット
plt.subplot(2, 2, 3)
plt.plot(n_values, E_T2_list, marker='o', label='シミュレーション')
plt.axhline(y=theoretical_variance_true, color='r', linestyle='--', label='理論値: $E[T^2] = \sigma^2$')
plt.title('$E[T^2]$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$E[T^2]$')
plt.legend()
# E[S^2] のプロット
plt.subplot(2, 2, 4)
plt.plot(n_values, E_S2_list, marker='o', label='シミュレーション')
plt.axhline(y=theoretical_variance_true, color='r', linestyle='--', label='理論値: $E[S^2] = \sigma^2$')
plt.title('$E[S^2]$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$E[S^2]$')
plt.legend()
# グラフの表示
plt.tight_layout()
plt.show()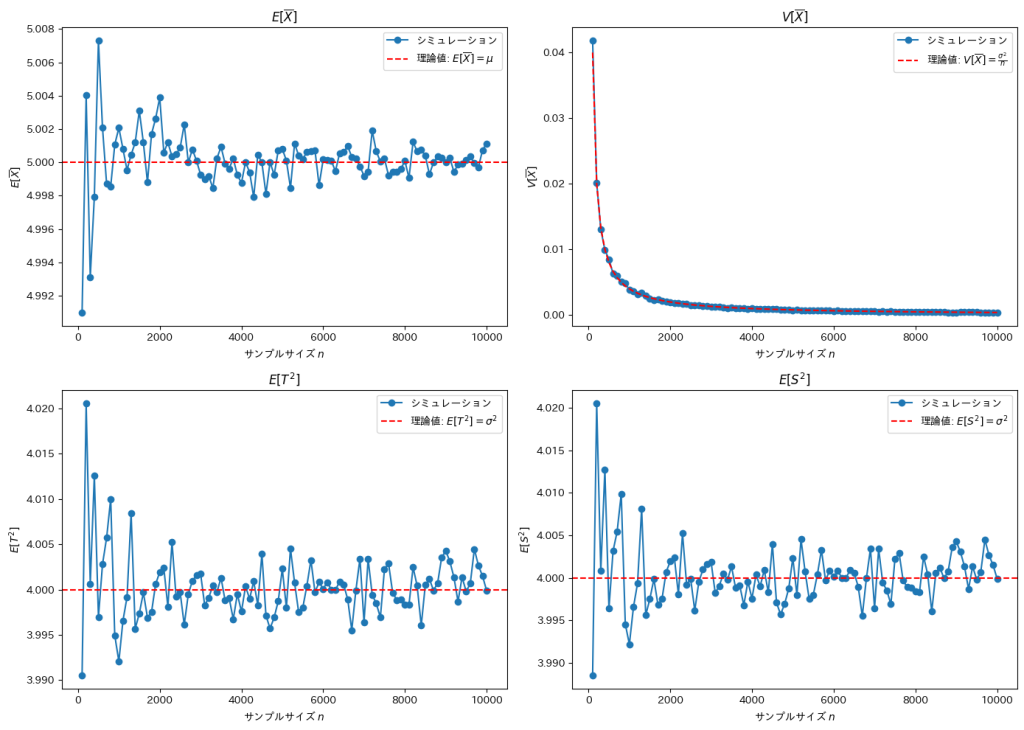
サンプルサイズnが増加するほど、各推定量は理論値に収束していく傾向に見えます。![]() と
と![]() は外れ値の影響を受けやすいため収束速度が緩やかです。
は外れ値の影響を受けやすいため収束速度が緩やかです。
2018 Q5(3)
一様分布の3つの順序統計量のうち第3と第1の確率変数の差の期待値と分散を求めました。
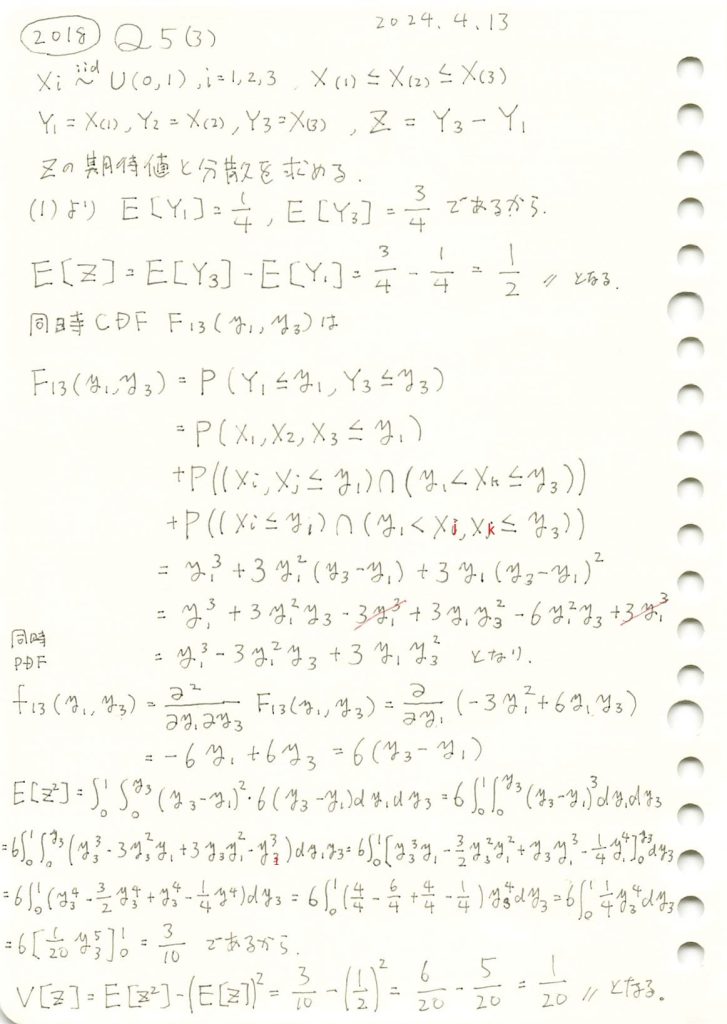
コード
同時確率密度関数f13(y1,y3)を視覚化してみます。またzが一定になる線も描画してみます。
# 2018 Q5(3) 2024.10.23
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 定義域 (y1 と y3 は [0, 1] の範囲で変動)
y1_values = np.linspace(0, 1, 100)
y3_values = np.linspace(0, 1, 100)
# メッシュグリッドを作成
Y1, Y3 = np.meshgrid(y1_values, y3_values)
# 同時確率密度関数 f13(y1, y3) = 6(y3 - y1), ただし y3 >= y1
f13 = np.where(Y3 >= Y1, 6 * (Y3 - Y1), 0)
# 等高線のための Z の値を設定 (例として Z = 0.2, 0.5, 0.8 を使用)
Z_values = [0.2, 0.5, 0.8]
# 3D グラフの描画を再度行う
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 3Dプロット (同時確率密度関数 f13(y1, y3))
ax.plot_surface(Y1, Y3, f13, cmap='viridis', alpha=0.8)
# 各 Z = Y3 - Y1 の線をプロット
for z_value in Z_values:
y1_line = np.linspace(0, 1 - z_value, 100)
y3_line = y1_line + z_value
ax.plot(y1_line, y3_line, zs=0, zdir='z', label=f'$Z = {z_value}$', lw=2)
# 軸ラベル
ax.set_title('同時確率密度関数 $f_{13}(y_1, y_3)$ と $Z = Y_3 - Y_1$', fontsize=14)
ax.set_xlabel('$y_1$', fontsize=12)
ax.set_ylabel('$y_3$', fontsize=12)
ax.set_zlabel('$f_{13}(y_1, y_3)$', fontsize=12)
# 凡例
ax.legend()
# グラフの表示
plt.show()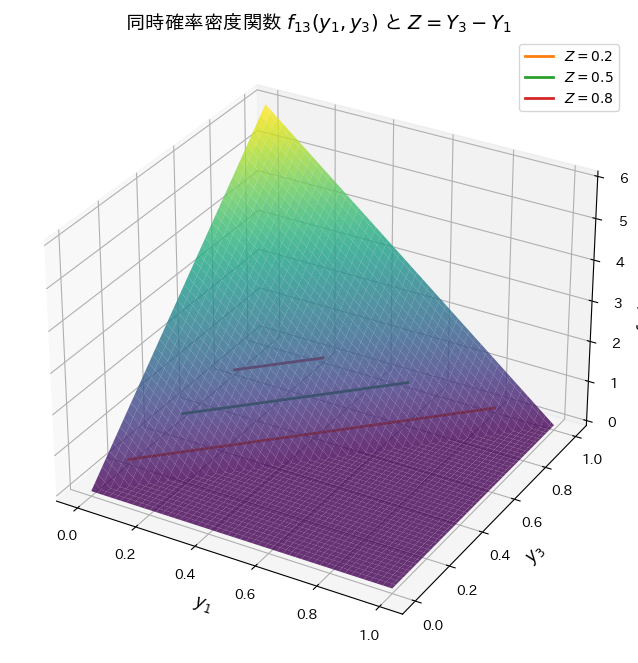
Z=z で垂直に切った断面の面積が![]() に相当します。
に相当します。
![]() を解いてZの確率密度関数を
を解いてZの確率密度関数を![]() のように求めます。順序統計量Y1とY3をシミュレーションし、理論と一致するか確認します。
のように求めます。順序統計量Y1とY3をシミュレーションし、理論と一致するか確認します。
# 2018 Q5(3) 2024.10.23
import numpy as np
import matplotlib.pyplot as plt
# サンプルデータの生成 (Z = Y3 - Y1 としてシミュレーション)
n_samples = 10000 # サンプル数
samples = np.random.uniform(0, 1, (n_samples, 3)) # 一様分布からサンプリング
Y1_samples = np.min(samples, axis=1) # 最小値 Y1
Y3_samples = np.max(samples, axis=1) # 最大値 Y3
# Z = Y3 - Y1 を計算
Z_samples = Y3_samples - Y1_samples
# Zの期待値と分散を計算
expected_Z = np.mean(Z_samples)
variance_Z = np.var(Z_samples)
# 理論値との比較
theoretical_Z_mean = 0.5
theoretical_Z_var = 1/20
# 期待値と分散を表示
print(f"シミュレーションによる E[Z](期待値): {expected_Z:.4f}, 理論値: {theoretical_Z_mean:.4f}")
print(f"シミュレーションによる Var[Z](分散): {variance_Z:.4f}, 理論値: {theoretical_Z_var:.4f}")
# Zの理論的な確率密度関数の定義
z_values = np.linspace(0, 1, 500)
f_z_theoretical = 6 * z_values * (1 - z_values)
# ヒストグラムと理論的なPDFを重ねて描画
plt.figure(figsize=(8, 6))
# サンプルのヒストグラムを描画 (確率密度として正規化)
plt.hist(Z_samples, bins=50, density=True, alpha=0.5, color='purple', label='Z samples (Y3 - Y1)')
# 理論的な確率密度関数のプロット
plt.plot(z_values, f_z_theoretical, label='Theoretical $f_Z(z) = 6z(1-z)$', color='black', linewidth=2)
# グラフの設定
plt.title('Z = Y3 - Y1 の確率密度関数 (シミュレーションと理論)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Z](期待値): 0.4992, 理論値: 0.5000
シミュレーションによる Var[Z](分散): 0.0500, 理論値: 0.0500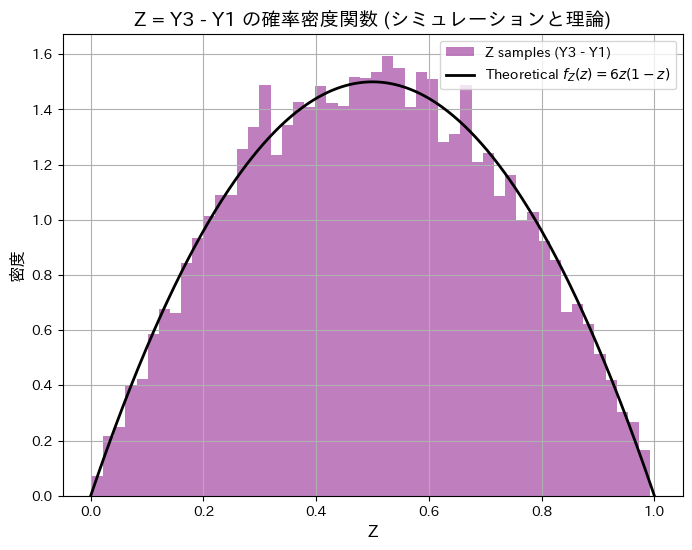
シミュレーションによる順序統計量Y3とY1の差の分布と期待値と分散が理論値と一致しました。
また興味深いことに、ZとY2は同じ分布になっていることが分かりました。
2018 Q5(2)
一様分布の3つの順序統計量のうち真ん中の確率密度関数と確率の計算をしました。
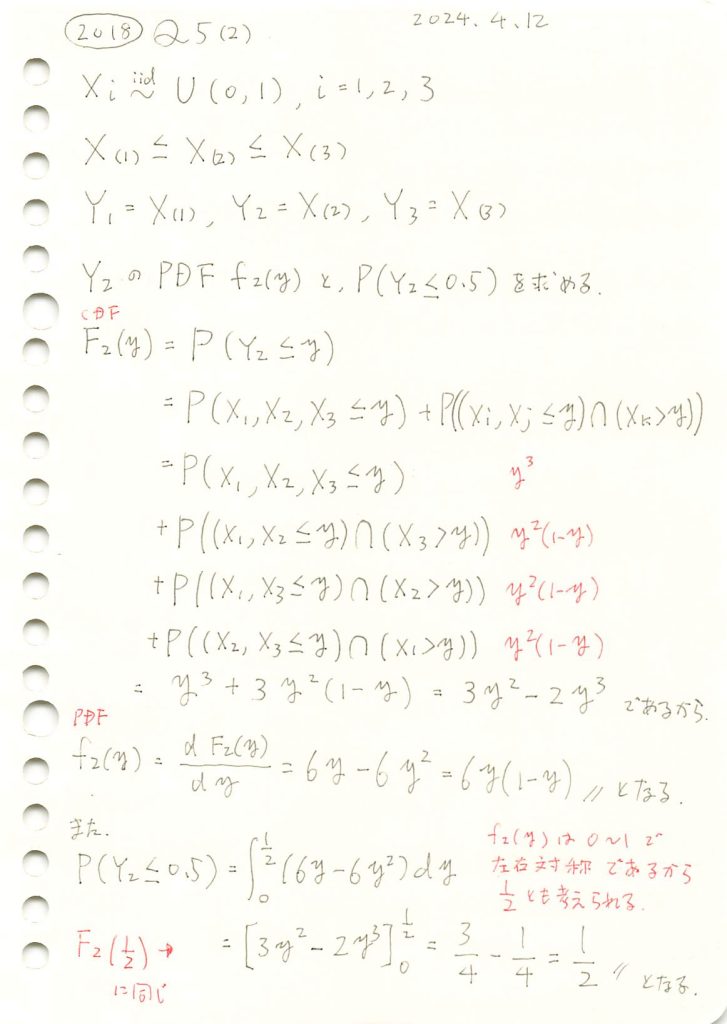
コード
シミュレーションにより順序統計量Y2の分布と期待値が理論値と一致するか確認します。
# 2018 Q5(2) 2024.10.22
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数 f2(y) の定義
f2_y = 6 * y_values * (1 - y_values)
# シミュレーションの設定
n_samples = 10000 # サンプル数
# 一様分布から3つの変数をサンプリング
samples = np.random.uniform(0, 1, (n_samples, 3))
# 順序統計量の第2要素を抽出 (Y2)
Y2_samples = np.median(samples, axis=1) # 中央値
# 期待値の計算
expected_Y2 = np.mean(Y2_samples)
# 理論値との比較
theoretical_Y2 = 0.5 # 中央値
# 期待値を表示
print(f"シミュレーションによる E[Y2](中間値の期待値): {expected_Y2:.4f}, 理論値: {theoretical_Y2:.4f}")
# ヒストグラムの作成
plt.figure(figsize=(8, 6))
# 理論密度関数 f2(y) のプロット
plt.plot(y_values, f2_y, label='$f_2(y) = 6y(1-y)$', color='red')
# サンプルのヒストグラムを追加 (確率密度として正規化)
plt.hist(Y2_samples, bins=50, density=True, alpha=0.5, color='red', label='Y2 samples (median)')
# グラフの設定
plt.title('確率密度関数 $f_2(y)$ とヒストグラム (シミュレーションと理論)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Y2](中間値の期待値): 0.5006, 理論値: 0.5000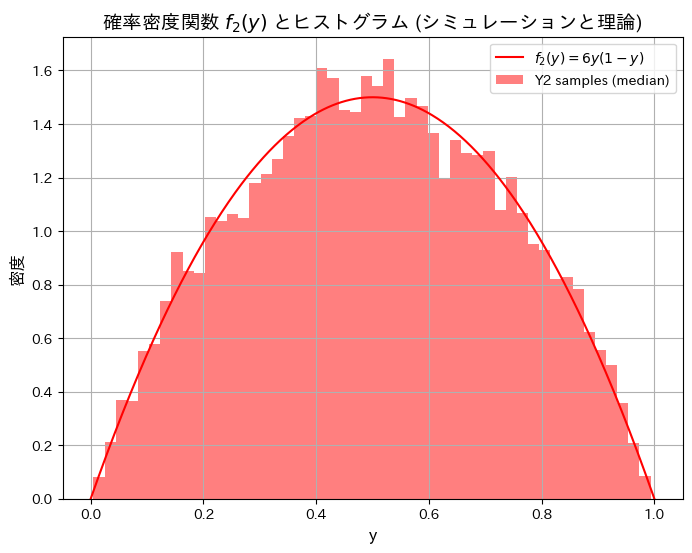
シミュレーションによる順序統計量Y1とY3の分布と期待値が理論値と一致しました。
次に、Y1~Y3の確率密度関数と累積分布関数を重ねて見てみます。
# 2018 Q5(2) 2024.10.22
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数の定義
f1_y = 3 * (1 - y_values) ** 2
f2_y = 6 * y_values * (1 - y_values)
f3_y = 3 * y_values ** 2
# CDF (累積分布関数) の計算
cdf1_y = np.cumsum(f1_y) * (y_values[1] - y_values[0])
cdf2_y = np.cumsum(f2_y) * (y_values[1] - y_values[0])
cdf3_y = np.cumsum(f3_y) * (y_values[1] - y_values[0])
# グラフの作成
plt.figure(figsize=(10, 8))
# 確率密度関数 (PDF) のプロット
plt.subplot(2, 1, 1)
plt.plot(y_values, f1_y, label='$f_1(y)$', color='blue')
plt.plot(y_values, f2_y, label='$f_2(y)$', color='red')
plt.plot(y_values, f3_y, label='$f_3(y)$', color='green')
plt.title('確率密度関数 (PDF)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# 累積分布関数 (CDF) のプロット
plt.subplot(2, 1, 2)
plt.plot(y_values, cdf1_y, label='$F_1(y)$', color='blue')
plt.plot(y_values, cdf2_y, label='$F_2(y)$', color='red')
plt.plot(y_values, cdf3_y, label='$F_3(y)$', color='green')
plt.title('累積分布関数 (CDF)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('累積確率', fontsize=12)
plt.legend(loc='lower right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()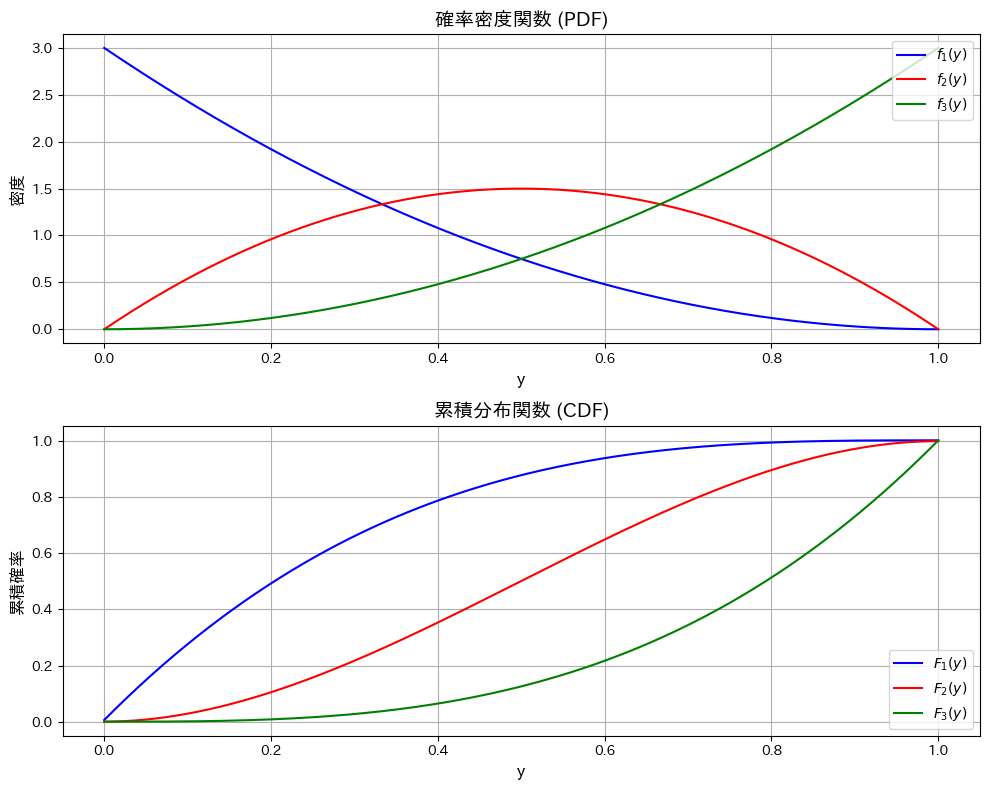
Y1は左寄り、Y2は中央寄り、Y3は右寄りになっていて、順序統計量の性質を直感的に表されています。Y2の確率密度関数は左右対称なので期待値が0.5になることも分かります。Y2の累積分布関数が直線でないことも面白いです。
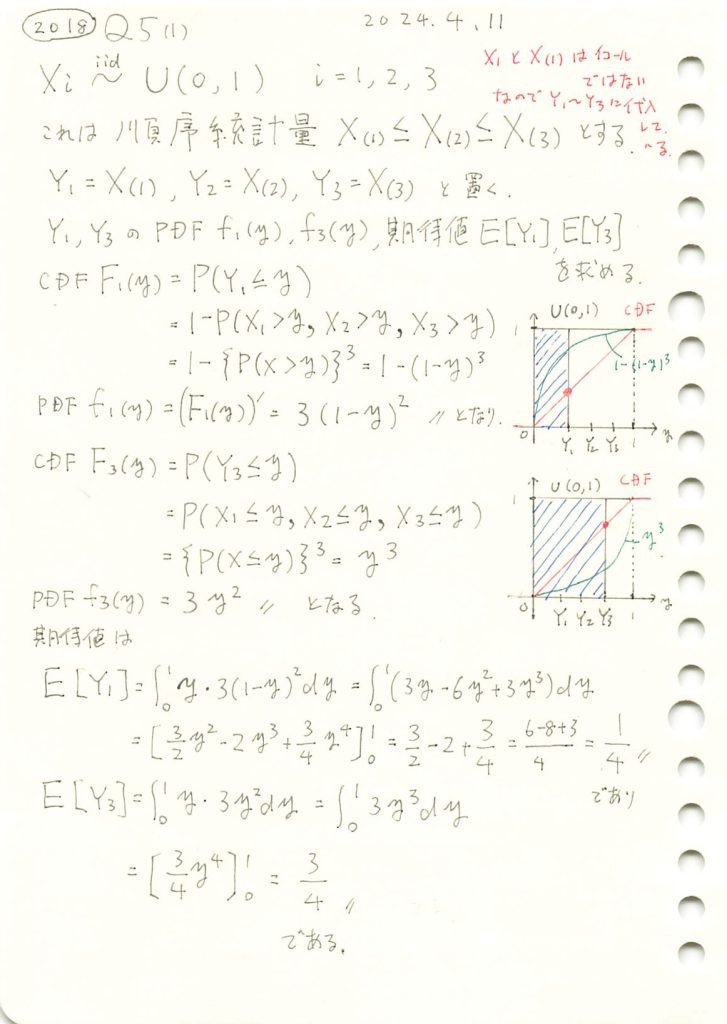
2018 Q5(1)
一様分布の順序統計量の確率密度関数と期待値を求めました。
コード
シミュレーションにより順序統計量Y1とY3の分布と期待値が理論値と一致するか確認します。
# 2018 Q5(1) 2024.10.21
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数の定義
f1_y = 3 * (1 - y_values) ** 2
f3_y = 3 * y_values ** 2
# シミュレーションの設定
n_samples = 10000 # サンプル数
# 一様分布から3つの変数をサンプリング
samples = np.random.uniform(0, 1, (n_samples, 3))
# 順序統計量を求める
Y1_samples = np.min(samples, axis=1) # 最小値
Y3_samples = np.max(samples, axis=1) # 最大値
# 期待値の計算
expected_Y1 = np.mean(Y1_samples)
expected_Y3 = np.mean(Y3_samples)
# 理論値との比較
theoretical_Y1 = 1/4
theoretical_Y3 = 3/4
# 期待値を表示
print(f"シミュレーションによる E[Y1](最小値の期待値): {expected_Y1:.4f}, 理論値: {theoretical_Y1:.4f}")
print(f"シミュレーションによる E[Y3](最大値の期待値): {expected_Y3:.4f}, 理論値: {theoretical_Y3:.4f}")
# ヒストグラムの作成
plt.figure(figsize=(8, 6))
# 理論密度関数のプロット
plt.plot(y_values, f1_y, label='$f_1(y) = 3(1-y)^2$', color='blue')
plt.plot(y_values, f3_y, label='$f_3(y) = 3y^2$', color='green')
# サンプルのヒストグラムを追加 (確率密度として正規化)
plt.hist(Y1_samples, bins=50, density=True, alpha=0.5, color='blue', label='Y1 samples (min)')
plt.hist(Y3_samples, bins=50, density=True, alpha=0.5, color='green', label='Y3 samples (max)')
# グラフの設定
plt.title('確率密度関数 $f_1(y)$ と $f_3(y)$ (シミュレーションと理論)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Y1](最小値の期待値): 0.2499, 理論値: 0.2500
シミュレーションによる E[Y3](最大値の期待値): 0.7487, 理論値: 0.7500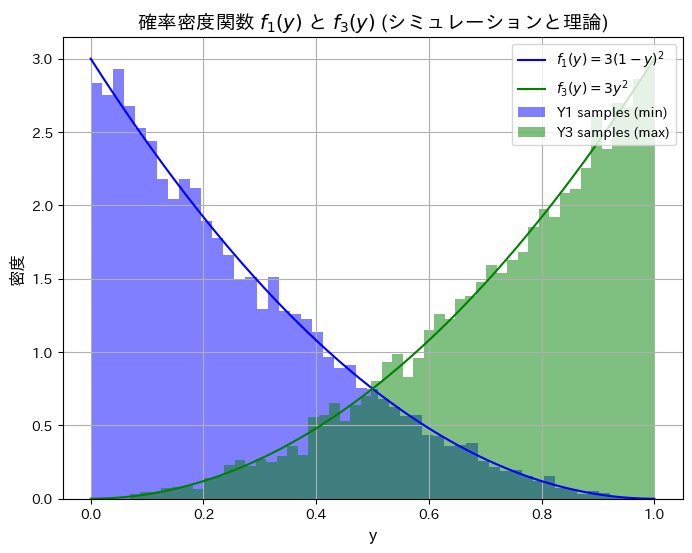
シミュレーションによる順序統計量Y1とY3の分布と期待値が理論値と一致しました。
2018 Q4(3)
マルコフ連鎖する条件付き正規分布の任意のtに対する分布の証明をやりました。

コード
![]() の条件付き分布が
の条件付き分布が![]() に従うのかシミュレーションをしてみます。
に従うのかシミュレーションをしてみます。
# 2018 Q4(3) 2024.10.20
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
t_max = 50 # 時間 t の最大値
n_simulations = 10000 # シミュレーション回数
rho = 0.7 # ρの値
x_0 = 1.0 # X_0 の初期値
# シミュレーション結果を格納するリスト
X_t_samples = np.zeros((t_max, n_simulations))
X_t_samples[0, :] = x_0 # X_0 = x_0
# マルコフプロセスをシミュレーション
for t in range(1, t_max):
# X_t を次のステップで生成
mean = rho**2 * X_t_samples[t-1, :]
variance = 1 - rho**4
X_t_samples[t, :] = np.random.normal(loc=mean, scale=np.sqrt(variance), size=n_simulations)
# シミュレーション結果の平均と分散を計算
simulated_means = np.mean(X_t_samples, axis=1)
simulated_variances = np.var(X_t_samples, axis=1)
# 理論値の期待値と分散を計算
theoretical_means = rho**(2 * np.arange(t_max)) * x_0
theoretical_variances = 1 - rho**(4 * np.arange(t_max))
# グラフを描画
plt.figure(figsize=(10, 6))
# 期待値のプロット
plt.subplot(2, 1, 1)
plt.plot(np.arange(t_max), simulated_means, label="シミュレーション期待値", color='blue', linestyle='--')
plt.plot(np.arange(t_max), theoretical_means, label="理論期待値", color='red')
plt.title("期待値の推移")
plt.xlabel("時間 t")
plt.ylabel("期待値 E[X_t]")
plt.legend()
plt.grid(True)
# 分散のプロット
plt.subplot(2, 1, 2)
plt.plot(np.arange(t_max), simulated_variances, label="シミュレーション分散", color='blue', linestyle='--')
plt.plot(np.arange(t_max), theoretical_variances, label="理論分散", color='red')
plt.title("分散の推移")
plt.xlabel("時間 t")
plt.ylabel("分散 Var[X_t]")
plt.legend()
plt.grid(True)
# グラフを表示
plt.tight_layout()
plt.show()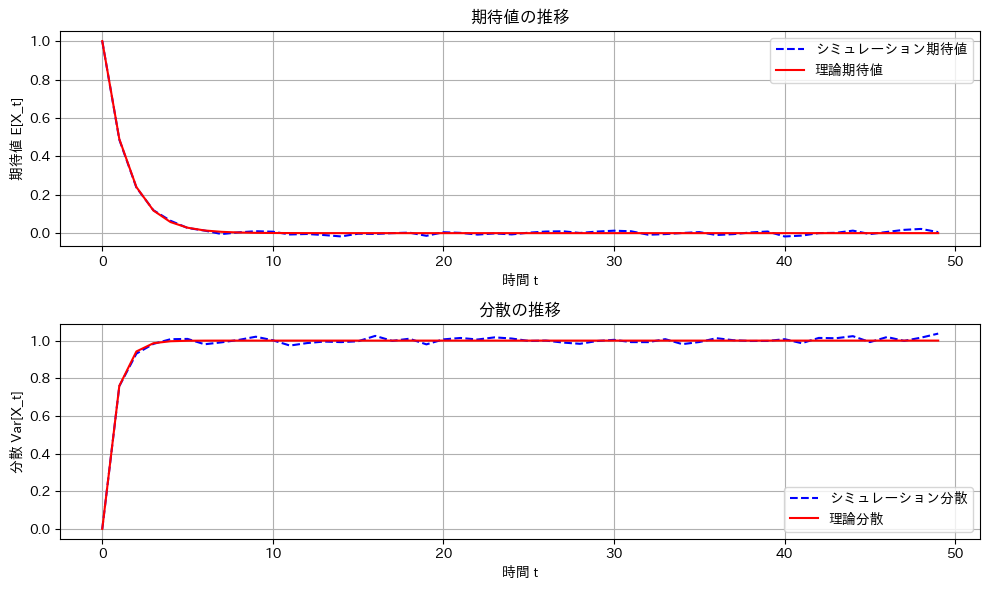
シミュレーションと理論値は一致しました。
2018 Q4(2)-2
マルコフ連鎖する条件付き正規分布の分散の問題をやりました。
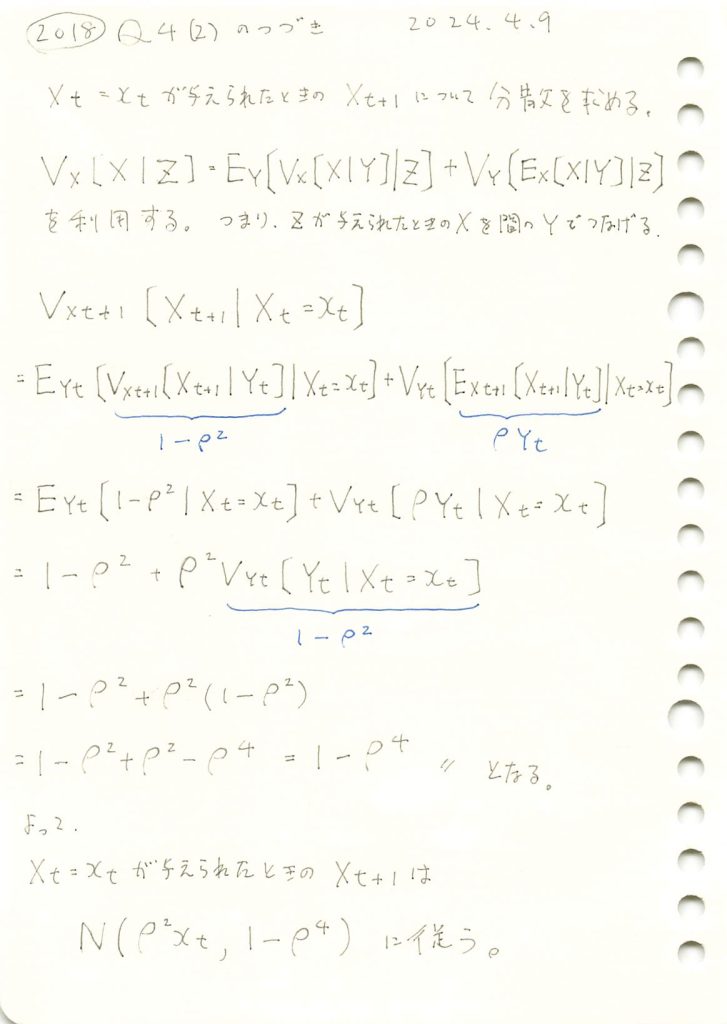
コード
![]() をシミュレーションしてみます。
をシミュレーションしてみます。
#2018 Q4(2) 2024.10.19
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n_simulations = 100000 # シミュレーション回数
rho = 0.7 # ρの値
x_t = 1.0 # X_t の初期値
# シミュレーション結果を格納するリスト
X_t1_samples = []
for _ in range(n_simulations):
# 1. X_t -> Y_t のステップ
y_t = np.random.normal(loc=rho * x_t, scale=np.sqrt(1 - rho**2))
# 2. Y_t -> X_{t+1} のステップ
x_t1 = np.random.normal(loc=rho * y_t, scale=np.sqrt(1 - rho**2))
# 結果をリストに追加
X_t1_samples.append(x_t1)
# シミュレーション結果を配列に変換
X_t1_samples = np.array(X_t1_samples)
# シミュレーション結果の期待値と分散を計算
simulated_mean = np.mean(X_t1_samples)
simulated_variance = np.var(X_t1_samples)
# 理論値の期待値と分散
expected_mean = rho**2 * x_t # 理論上の期待値
expected_variance = 1 - rho**4 # 理論上の分散
# 結果の表示
print(f"理論上の期待値: {expected_mean}, シミュレーションによる期待値: {simulated_mean}")
print(f"理論上の分散: {expected_variance}, シミュレーションによる分散: {simulated_variance}")
# ヒストグラムの表示
plt.hist(X_t1_samples, bins=50, density=True, alpha=0.6, color='g', edgecolor='black', label='シミュレーション')
plt.axvline(expected_mean, color='r', linestyle='--', label=f'理論上の期待値: {expected_mean:.3f}')
plt.title(r"$X_{t+1}$ のシミュレーション (マルコフ性)")
plt.xlabel(r"$X_{t+1}$ の値")
plt.ylabel("頻度")
plt.legend()
plt.grid(True)
plt.show()理論上の期待値: 0.48999999999999994, シミュレーションによる期待値: 0.4909842816275996
理論上の分散: 0.7599, シミュレーションによる分散: 0.7608618418358614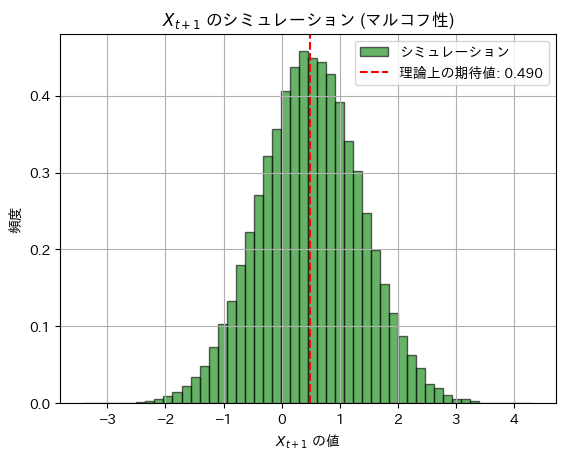
シミュレーション結果は理論値に一致しました。
2018 Q4(2)-1
マルコフ連鎖する条件付き正規分布の期待値の問題をやりました。
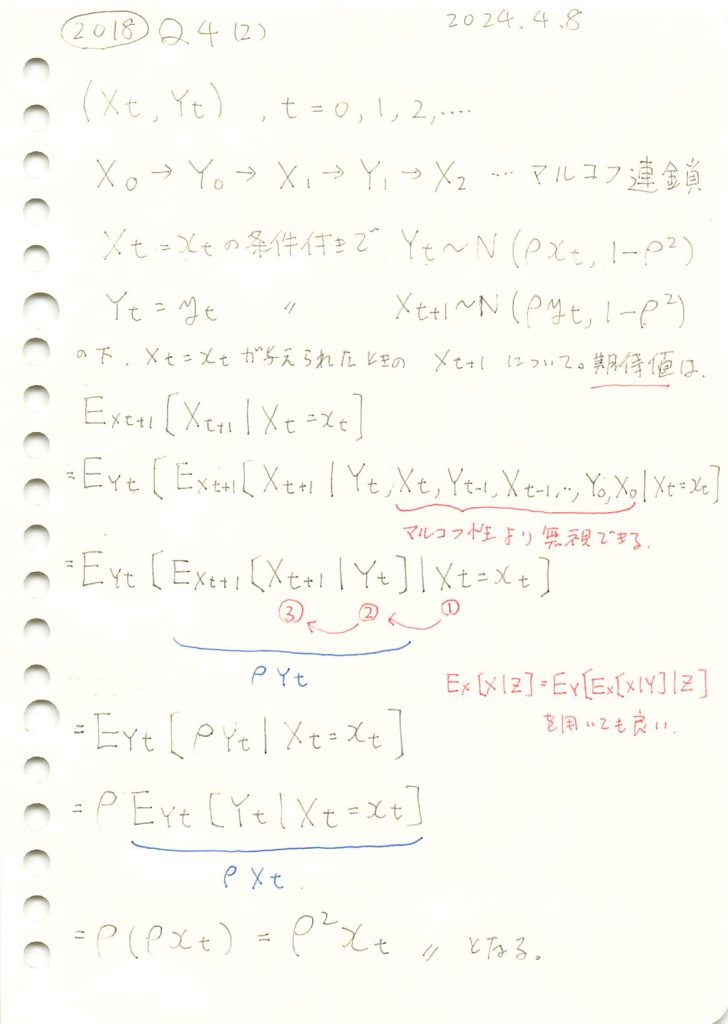
コード
![]() をシミュレーションしてみます。
をシミュレーションしてみます。
#2018 Q4(2) 2024.10.19
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n_simulations = 100000 # シミュレーション回数
rho = 0.7 # ρの値
x_t = 1.0 # X_t の初期値
# シミュレーション結果を格納するリスト
X_t1_samples = []
for _ in range(n_simulations):
# 1. X_t -> Y_t のステップ
y_t = np.random.normal(loc=rho * x_t, scale=np.sqrt(1 - rho**2))
# 2. Y_t -> X_{t+1} のステップ
x_t1 = np.random.normal(loc=rho * y_t, scale=np.sqrt(1 - rho**2))
# 結果をリストに追加
X_t1_samples.append(x_t1)
# シミュレーション結果を配列に変換
X_t1_samples = np.array(X_t1_samples)
# シミュレーション結果の期待値と分散を計算
simulated_mean = np.mean(X_t1_samples)
simulated_variance = np.var(X_t1_samples)
# 理論値の期待値と分散
expected_mean = rho**2 * x_t # 理論上の期待値
expected_variance = 1 - rho**4 # 理論上の分散
# 結果の表示
print(f"理論上の期待値: {expected_mean}, シミュレーションによる期待値: {simulated_mean}")
print(f"理論上の分散: {expected_variance}, シミュレーションによる分散: {simulated_variance}")
# ヒストグラムの表示
plt.hist(X_t1_samples, bins=50, density=True, alpha=0.6, color='g', edgecolor='black', label='シミュレーション')
plt.axvline(expected_mean, color='r', linestyle='--', label=f'理論上の期待値: {expected_mean:.3f}')
plt.title(r"$X_{t+1}$ のシミュレーション (マルコフ性)")
plt.xlabel(r"$X_{t+1}$ の値")
plt.ylabel("頻度")
plt.legend()
plt.grid(True)
plt.show()理論上の期待値: 0.48999999999999994, シミュレーションによる期待値: 0.4909842816275996
理論上の分散: 0.7599, シミュレーションによる分散: 0.7608618418358614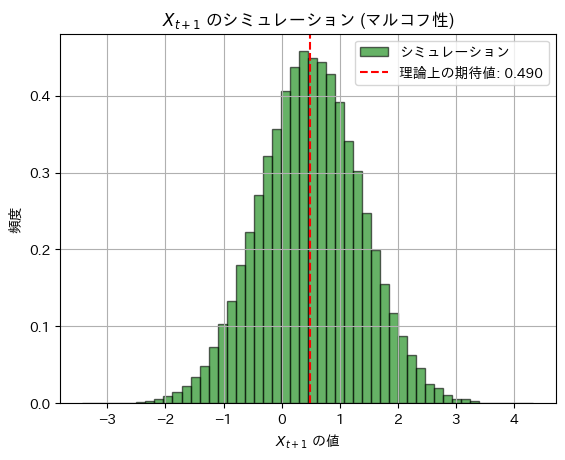
シミュレーション結果は理論値に一致しました。
2018 Q4(1)
条件付きの正規分布の周辺確率密度関数を求めました。

コード
条件付き分布Y|X=x を生成し、Yの周辺分布が標準正規分布に従うかシミュレーションしてみます。
# 2018 Q4(1) 2024.10.18
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# パラメータ設定
rho = 0.7 # 相関係数
# サンプルサイズ
n_samples = 10000
#Xを標準正規分布からサンプル
X = np.random.normal(0, 1, n_samples)
#Y|X=x に基づいてYを生成
Y = np.random.normal(rho * X, np.sqrt(1 - rho**2))
#Yのヒストグラムを描画
plt.hist(Y, bins=50, density=True, alpha=0.6, color='g', label='シミュレーションされた Y')
# 理論的な標準正規分布N(0,1)の曲線を重ねる
x_vals = np.linspace(-4, 4, 1000)
plt.plot(x_vals, norm.pdf(x_vals, 0, 1), 'r-', lw=2, label='理論分布 N(0,1)')
# ラベルを描画
plt.title('シミュレーションされた Y と理論分布 N(0,1) の比較')
plt.xlabel('Y')
plt.ylabel('確率密度')
plt.legend()
# グラフを表示
plt.show()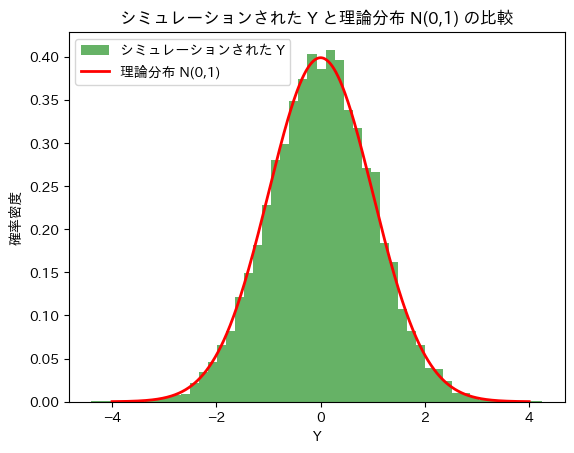
Yは標準正規分布に従うことが確認できました。
2018 Q3(5)
二項分布の条件付き確率質量関数のパラメータの最尤推定の問題をやりました。

コード
![]() として、
として、 ![]() より
より![]() を求めます。まずはfsolveを使用してモーメント法による推定値を求めてみます。
を求めます。まずはfsolveを使用してモーメント法による推定値を求めてみます。
# 2018 Q3(5) 2024.10.17
from scipy.optimize import fsolve
# パラメータ設定
n = 8 # 試行回数
observed_mean = 3.5 # 仮定した標本平均
# モーメント法の方程式
def moment_eq(theta, observed_mean, n):
return observed_mean - (n * theta) / (1 - (1 - theta)**n)
# 数値的に方程式を解く
theta_hat = fsolve(moment_eq, 0.1, args=(observed_mean, n))[0]
# 結果を表示
print(f"θ ハット: {theta_hat}")θ ハット: 0.4328142334547646求まりました。
次に反復計算で解いてみます。
# 2018 Q3(5) 2024.10.17
import numpy as np
# パラメータ設定
n = 8 # 試行回数
observed_mean = 3.5 # 仮定された標本平均
max_iterations = 100 # 最大反復回数
tolerance = 1e-6 # 収束判定の閾値
# 初期推定値
theta_hat = observed_mean / n
# 反復計算
for iteration in range(max_iterations):
new_theta_hat = (observed_mean / n) * (1 - (1 - theta_hat) ** n)
# 収束判定
if abs(new_theta_hat - theta_hat) < tolerance:
break
theta_hat = new_theta_hat
# 結果の表示
print(f"θ ハット: {theta_hat}")θ ハット: 0.432814320144486同じ値になりました。
次は単純にθを0.01から0.99まで変化させて![]() が1になるθを見つけます。
が1になるθを見つけます。
# 2018 Q3(5) 2024.10.17
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 8 # 試行回数
observed_mean = 3.5 # 仮定した標本平均
theta_values = np.linspace(0.01, 0.99, 100) # θを0.01から0.99まで100点で変化させる
# f(θ) の定義
def f_theta(theta, n, observed_mean):
return (n * theta) / (observed_mean * (1 - (1 - theta) ** n))
# f(θ) を計算
f_values = f_theta(theta_values, n, observed_mean)
# f(θ) = 1 となる交点を見つける
intersection_index = np.argmin(np.abs(f_values - 1))
theta_hat = theta_values[intersection_index]
# 交点の θ ハットの値を表示
print(f"θ ハット: {theta_hat}")
# グラフの描画
plt.plot(theta_values, f_values, label='f(θ)', color='blue')
plt.axhline(y=1, color='red', linestyle='--', label='y = 1')
plt.xlabel("θ", fontsize=12)
plt.ylabel("f(θ)", fontsize=12)
plt.title("f(θ) のグラフ (左辺 / 右辺の比)", fontsize=14)
plt.legend()
plt.grid(True)
# グラフの表示
plt.show()θ ハット: 0.43565656565656563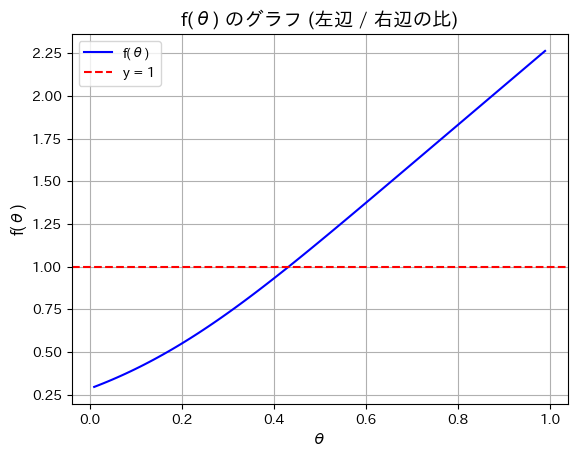
概ね同じ値になりました。
2018 Q3(4)
二項分布の期待値と条件付き期待値との比が2倍になるパラメータを求めました。

コード
n=8に固定しθを変化させて、η(θ)、E[X]、2E[X]の理論値をプロットしてみます。
# 2018 Q3(4) 2024.10.16
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 8 # 試行回数
theta_values = np.linspace(0.01, 0.2, 50) # θを0.01から0.2まで50点で変化
# 条件付き期待値 η(θ) と 条件なしの期待値 E[X] を計算
eta_values = n * theta_values / (1 - (1 - theta_values) ** n) # η(θ)
EX_values = n * theta_values # E[X]
# 二倍のE[X]をプロットするための値
double_EX_values = 2 * EX_values
# グラフの描画
plt.plot(theta_values, eta_values, label='条件付き期待値 η(θ)', color='blue', linestyle='-', marker='o', markersize=4)
plt.plot(theta_values, EX_values, label='条件なし期待値 E[X]', color='green', linestyle='--')
plt.plot(theta_values, double_EX_values, label='2倍の E[X]', color='red', linestyle=':')
# 二倍の関係になるθの位置を求め、プロット
intersection_index = np.argmin(np.abs(eta_values - double_EX_values))
intersection_theta = theta_values[intersection_index]
intersection_eta = eta_values[intersection_index]
plt.scatter(intersection_theta, intersection_eta, color='black', zorder=5, label=f'η(θ) = 2E[X] (θ ≈ {intersection_theta:.3f})')
# キャプションの表示
plt.xlabel("θ", fontsize=12)
plt.ylabel("期待値", fontsize=12)
plt.title("θ に対する η(θ) と E[X] の比較 (理論値)", fontsize=14)
plt.legend()
plt.grid(True)
# グラフの表示
plt.show()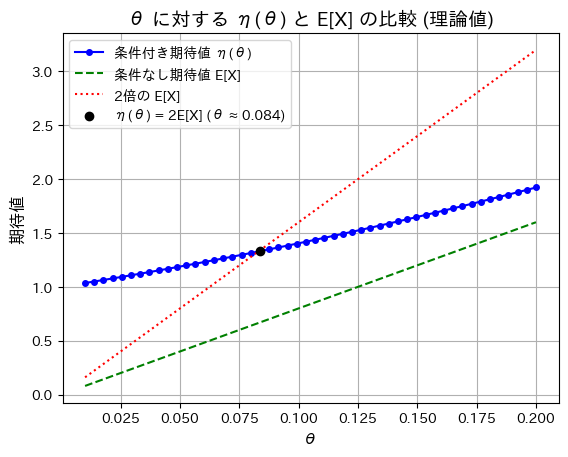
θ=0.083辺りで、η(θ)=2E[X]となることが確認できました。
次に、シミュレーションし同様に描画してみます。
# 2018 Q3(4) 2024.10.16
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 8 # 試行回数
theta_values = np.linspace(0.01, 0.2, 50) # θを0.01から0.2まで50点で変化
num_simulations = 100000 # シミュレーション回数
# シミュレーションによる条件付き期待値 η(θ) と 条件なし期待値 E[X] を計算
eta_values = []
EX_values = []
for theta in theta_values:
# 二項分布のサンプリング
binom_samples = np.random.binomial(n, theta, num_simulations)
# 条件付きサンプル (X >= 1)
samples_X_geq_1 = binom_samples[binom_samples >= 1]
# 条件付き期待値 η(θ)
eta = np.mean(samples_X_geq_1)
eta_values.append(eta)
# 条件なし期待値 E[X]
EX = np.mean(binom_samples)
EX_values.append(EX)
# 2倍のE[X]を計算
double_EX_values = 2 * np.array(EX_values)
# グラフの描画
plt.plot(theta_values, eta_values, label='条件付き期待値 η(θ)', color='blue', linestyle='-', marker='o', markersize=4)
plt.plot(theta_values, EX_values, label='条件なし期待値 E[X]', color='green', linestyle='--')
plt.plot(theta_values, double_EX_values, label='2倍の E[X]', color='red', linestyle=':')
# 二倍の関係になるθの位置を求め、プロット
intersection_index = np.argmin(np.abs(np.array(eta_values) - double_EX_values))
intersection_theta = theta_values[intersection_index]
intersection_eta = eta_values[intersection_index]
plt.scatter(intersection_theta, intersection_eta, color='black', zorder=5, label=f'η(θ) = 2E[X] (θ ≈ {intersection_theta:.3f})')
# キャプションの表示
plt.xlabel("θ", fontsize=12)
plt.ylabel("期待値", fontsize=12)
plt.title("θ に対する η(θ) と E[X] の比較 (シミュレーション)", fontsize=14)
plt.legend()
plt.grid(True)
# グラフの表示
plt.show()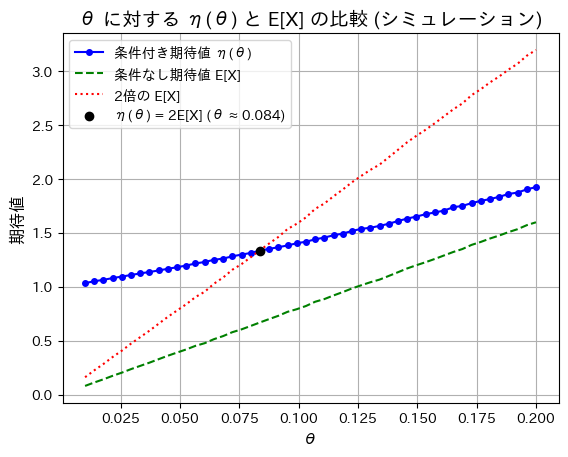
シミュレーションも同じ結果になりました。