ホーム » 十分統計量
「十分統計量」カテゴリーアーカイブ
2019 Q3(1)
一様分布に於いて最大値が十分統計量であることを示しました。

コード
一様分布の最大値Yを元に、不偏推定量![]() を計算します。
を計算します。
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータ
n = 10 # サンプルサイズ
theta_true = 10 # 真のθ
num_simulations = 1000 # シミュレーション回数
# θの推定値を格納するリスト
theta_estimates = []
# シミュレーション開始
for _ in range(num_simulations):
# (0, theta_true) の一様分布からn個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# 最大値 Y = max(X_1, ..., X_n)
Y = np.max(samples)
# Y から θ を推定 (最大値を使って推定)
theta_hat = Y * (n / (n - 1)) # 推定式: Y * n / (n-1)
# 推定されたθをリストに保存
theta_estimates.append(theta_hat)
# θの推定値の平均を計算
theta_mean = np.mean(theta_estimates)
# 推定結果をヒストグラムで表示
plt.hist(theta_estimates, bins=30, alpha=0.7, color='blue', edgecolor='black', label='推定されたθ')
plt.axvline(x=theta_true, color='red', linestyle='--', label=f'真のθ = {theta_true}')
plt.axvline(x=theta_mean, color='green', linestyle='--', label=f'推定されたθの平均 = {theta_mean:.2f}')
plt.title(f'Y (最大値) に基づく θ の推定値のヒストグラム ({n} サンプル)')
plt.xlabel('推定された θ')
plt.ylabel('頻度')
plt.legend()
plt.show()
# 推定結果をテキストで表示
print(f'真のθ: {theta_true}')
print(f'推定されたθの平均: {theta_mean:.2f}')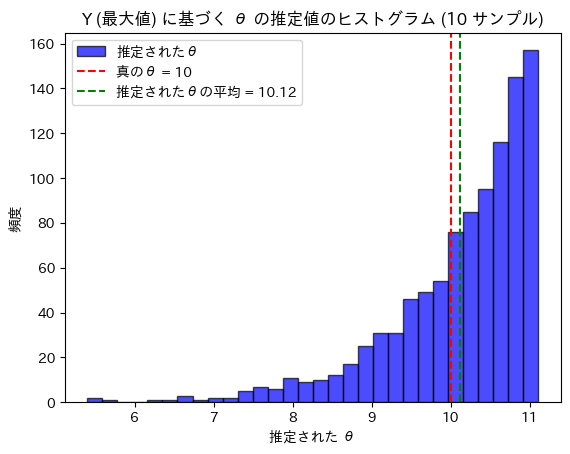
真のθ: 10
推定されたθの平均: 10.12推定されたθは真のθに近い値を取りました。最大値Yだけを用いてθが正確に推定できたので、Yはθに関する十分統計量であることが確認できました。
2021 Q3(2)[2-2]
ポアソン分布に従う独立な変数の和はパラメータλの十分統計量であることを学びました。
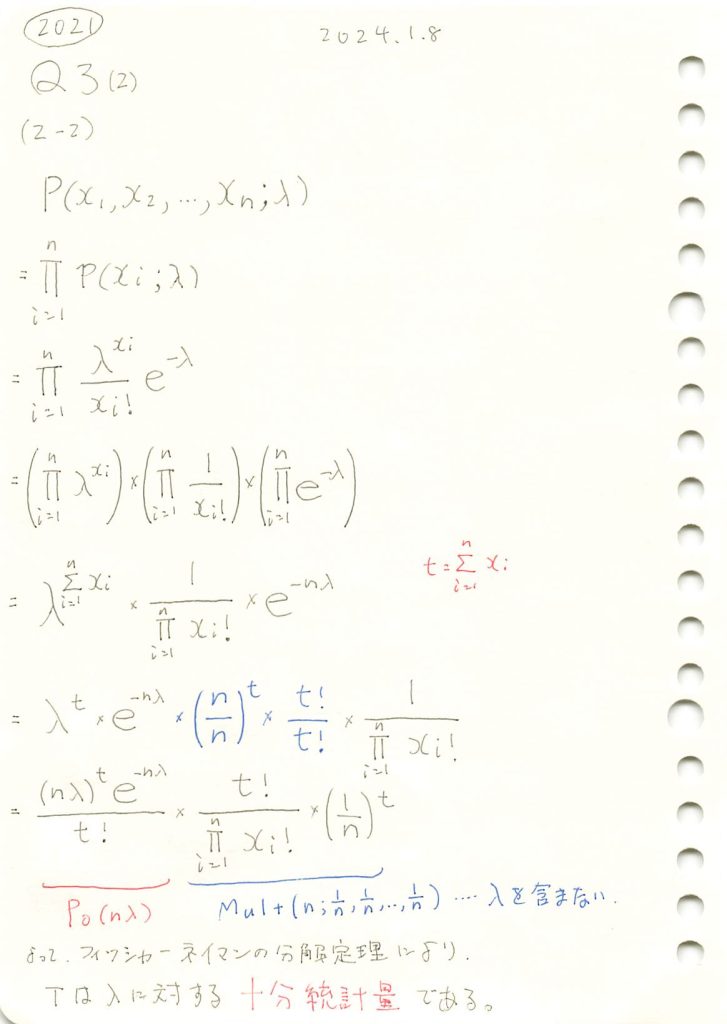
あとがき
![]() の式で示すと簡単。
の式で示すと簡単。
コード
ポアソン分布に従う10個の乱数の和 Tの分布を見てみます。
# 2024 Q3(2)[2-2] 2024.8.27
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
lambda_value = 5 # 真のパラメータ
n = 10 # サンプル数
num_simulations = 1000000 # シミュレーション回数
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_value, (num_simulations, n))
# 和 T を計算
T = np.sum(samples, axis=1)
# 和 T のヒストグラムをプロット
plt.hist(T, bins=30, density=True, alpha=0.75, color='blue')
plt.title(f'Tの分布 (n 個のポアソン変数の和)')
plt.xlabel('T')
plt.ylabel('確率密度')
plt.grid(True)
plt.show()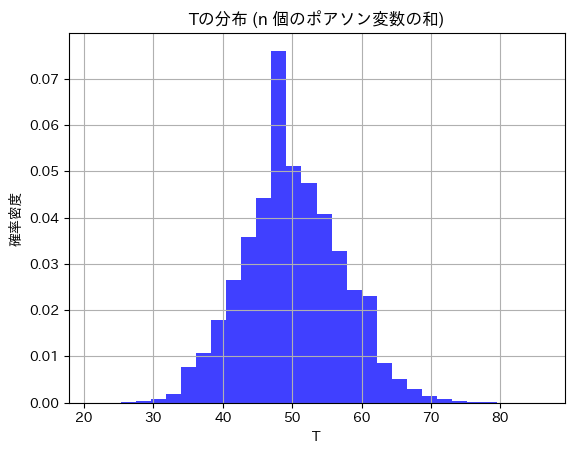
T~Po(nλ)になっています。
つぎにT=50の条件下での確率変数X1の分布を見てます。
# 2024 Q3(2)[2-2] 2024.8.27
import numpy as np
import matplotlib.pyplot as plt
# 条件付き分布の確認
# 例えば、T = 50 の場合におけるサンプルの分布を確認
T_value = 50 # T の特定の値
samples_given_T = samples[np.sum(samples, axis=1) == T_value]
# 確率変数の1つ (X1) の分布をプロット
plt.hist(samples_given_T[:, 0], bins=15, density=True, alpha=0.75, color='green')
plt.title(f'T={T_value} の条件付き X1 の分布')
plt.xlabel('X1')
plt.ylabel('確率密度')
plt.grid(True)
plt.show()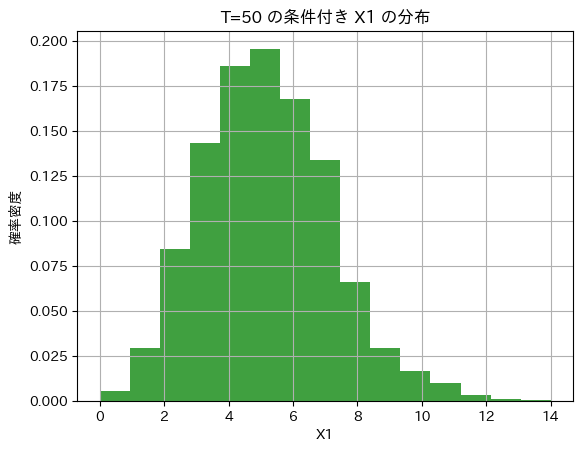
二項分布に従っているようです。
異なるλに対して、和T=50の条件下でのX1の分布を重ねて見てます。
# 2024 Q3(2)[2-2] 2024.8.27
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
# パラメータ設定
lambda_values = [3, 5, 7] # 異なる λ の値
n = 10 # サンプル数
num_simulations = 1000000 # シミュレーション回数
T_value = 50 # T の特定の値
plt.figure(figsize=(12, 6))
for lambda_value in lambda_values:
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_value, (num_simulations, n))
# T = T_value のサンプルを抽出
samples_given_T = samples[np.sum(samples, axis=1) == T_value]
# X1 の分布をプロット
counts, bin_edges, _ = plt.hist(samples_given_T[:, 0], bins=15, density=True, alpha=0.5, label=f'λ = {lambda_value}')
# 理論二項分布を描画
x1_min, x1_max = np.min(samples_given_T[:, 0]), np.max(samples_given_T[:, 0])
x = np.arange(x1_min, x1_max + 1)
estimated_p = 1 / n # 二項分布の p は 1/n で推定
binom_pmf = binom.pmf(x, T_value, estimated_p)
plt.plot(x, binom_pmf, 'k--', label=f'理論二項分布 Bin(T={T_value}, p=1/{n})')
plt.title(f'X1の分布 (T={T_value} 条件付き) と理論二項分布')
plt.xlabel('X1')
plt.ylabel('確率密度')
plt.legend()
plt.grid(True)
plt.show()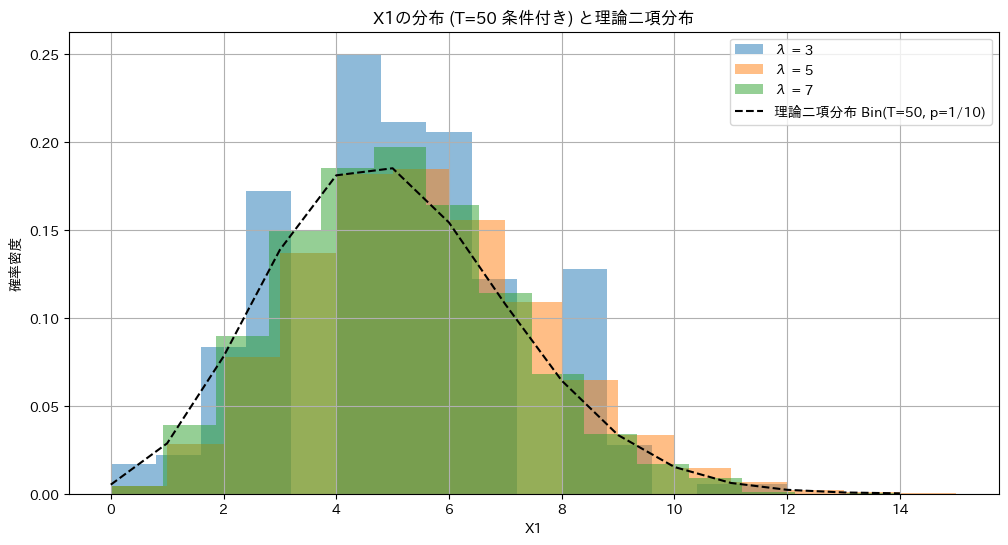
λに依存せず同じ二項分布に従います。よって統計量Tはλに対する十分統計量であることが示されました。
なお、X1~Xnの組は多項分布に従うが、簡単のためX1のみの分布を確認しました。X1は二項分布に従います。