ホーム » 検出力
「検出力」カテゴリーアーカイブ
2015 Q2(5)
前問の検定がネイマン-ピアソンの基本定理に基づき一様最強力検定であることを示しました。

コード
有意水準α=0.05のもと、検出力を理論値とシミュレーションで描画し比較します。
# 2015 Q2(5) 2024.12.11
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# シミュレーション設定
alpha = 0.05 # 有意水準
z_alpha = norm.ppf(1 - alpha) # 臨界値 z_alpha
num_simulations = 10000 # シミュレーション回数
n = 10 # 標本サイズ
mu_values = np.linspace(0, 2, 10) # 真の平均 μ の範囲
# 臨界値の計算
critical_value = z_alpha / np.sqrt(n) # 棄却域の閾値
# 検出力を計算する関数
def compute_power_for_mu(mu, n, z_alpha):
return 1 - norm.cdf(z_alpha - mu * np.sqrt(n))
# シミュレーションで検出力を計算
empirical_powers = []
for mu in mu_values:
samples = np.random.normal(mu, 1 / np.sqrt(n), num_simulations) # 標本生成
rejection_rate = np.mean(samples > critical_value) # 棄却割合
empirical_powers.append(rejection_rate)
# 理論的な検出力を計算
theoretical_powers = [compute_power_for_mu(mu, n, z_alpha) for mu in mu_values]
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(mu_values, theoretical_powers, label="理論的検出力", linestyle="--", color="blue")
plt.scatter(mu_values, empirical_powers, label="シミュレーションによる検出力", color="red", zorder=5)
plt.axhline(y=0.05, color="green", linestyle="--", label="有意水準 $\\alpha = 0.05$")
# グラフ設定
plt.xlabel("真の平均 $\\mu$", fontsize=12)
plt.ylabel("検出力 (Power)", fontsize=12)
plt.title("理論値とシミュレーションによる検出力の比較", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()
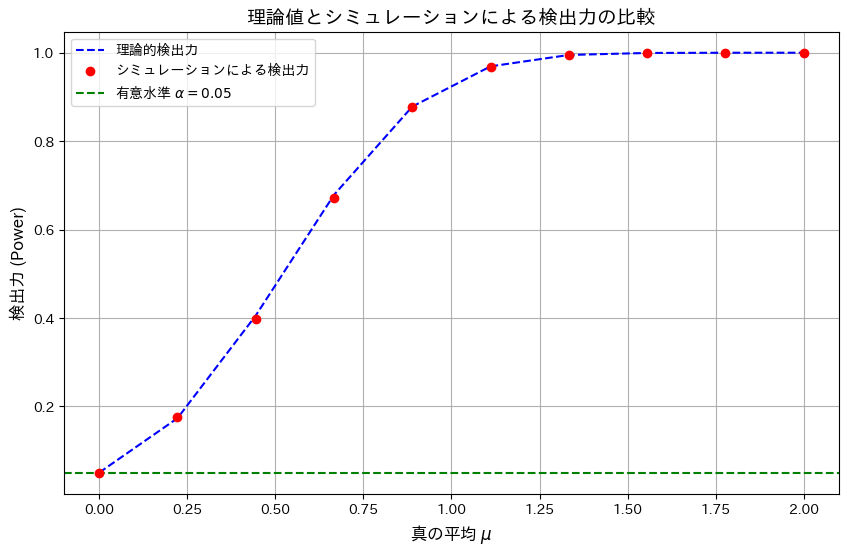
検出力は理論値とシミュレーションでよく一致し、検定が正しく機能していることを確認しました。また、真の平均μ>0に対して検出力が単調増加することが分かり、この検定が一様最強力検定の特徴を備えていることが確認できました。
2015 Q2(4)
標本平均の片側検定での検出力を特定の値以上にするために必要なサンプル数を求めました。
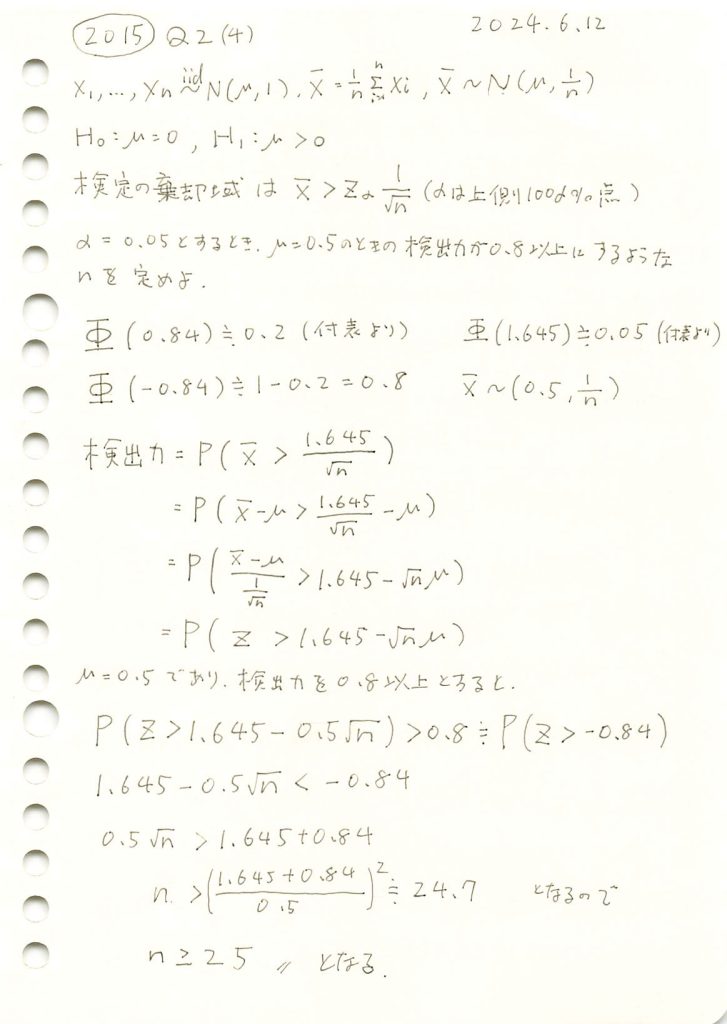
コード
有意水準α=0.05において、標本サイズnと検出力の関係を理論値とシミュレーションで比較し、目標の検出力0.8を達成するために必要な標本サイズnを調べます。
# 2015 Q2(4) 2024.12.10
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 設定
alpha = 0.05 # 有意水準
target_power = 0.8 # 目標検出力
mu = 0.5 # 真の平均
z_alpha = norm.ppf(1 - alpha) # 臨界値 z_alpha
z_power = norm.ppf(target_power) # 検出力に対応する Z 値
# 理論的な検出力の計算
n_values = np.arange(1, 51, 1) # 標本の大きさ n = 1, 2, ..., 50
powers_theoretical = [1 - norm.cdf(z_alpha - mu * np.sqrt(n)) for n in n_values]
# 実際の検出力を乱数シミュレーションで計算
num_simulations = 10000 # シミュレーション回数
n_sim_values = np.arange(5, 51, 5) # n = 5, 10, ..., 50
powers_simulated = []
for n in n_sim_values:
# 標本平均を生成
samples = np.random.normal(mu, 1 / np.sqrt(n), num_simulations)
# 標本平均が臨界値を超えた割合を計算
rejection_rate = np.mean(samples > z_alpha / np.sqrt(n))
powers_simulated.append(rejection_rate)
# グラフの描画
plt.figure(figsize=(10, 6))
# 理論的な検出力の曲線
plt.plot(n_values, powers_theoretical, label="理論的な検出力 (Power)", color="blue")
# シミュレーションによる検出力
plt.scatter(n_sim_values, powers_simulated, color="red", label="シミュレーションによる検出力", zorder=5)
# 検出力の目標ラインと必要な標本サイズライン
plt.axhline(y=target_power, color="red", linestyle="--", label=f"目標検出力 Power = {target_power}")
plt.axvline(x=25, color="green", linestyle="--", label="必要な標本数 n = 25")
# グラフの設定
plt.xlabel("標本の大きさ $n$", fontsize=12)
plt.ylabel("検出力 (Power)", fontsize=12)
plt.title("理論値とシミュレーションによる検出力の比較", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()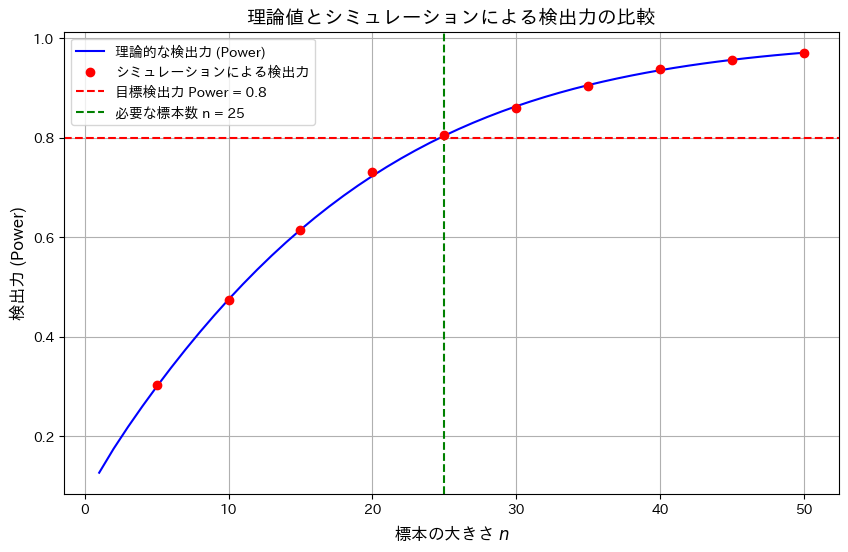
標本サイズnの増加が検出力の向上に寄与することを確認しました。また理論とシミュレーション結果が一致し、目標の検出力0.8を達成するためにはn=25が必要であることが確認できました。
2015 Q2(3)
標本平均の片側検定での検出力を求め、母平均と検出力の関係を描きました。

コード
有意水準 α=0.05、サンプルサイズ n=9およびn=16の場合における検出力を真の平均 μを変化させて視覚化します。また、μ=0.4,0.8での検出力を計算します。
# 2015 Q2(3) 2024.12.9
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 定義
alpha = 0.05 # 有意水準
z_alpha = norm.ppf(1 - alpha) # 臨界値 z_alpha
sample_sizes = [9, 16] # n = 9, 16
true_means = [0.4, 0.8] # 真の平均 μ = 0.4, 0.8
# 検出力の計算関数
def compute_power(mu, n, z_alpha):
z_value = z_alpha - mu * np.sqrt(n)
power = 1 - norm.cdf(z_value)
return power
# 検出力を計算
mu_values = np.linspace(0, 1.5, 100) # 真の平均 μ の範囲
powers_n9 = [compute_power(mu, n=9, z_alpha=z_alpha) for mu in mu_values]
powers_n16 = [compute_power(mu, n=16, z_alpha=z_alpha) for mu in mu_values]
# 指定された μ = 0.4, 0.8 の検出力を計算
specific_powers = {
(n, mu): compute_power(mu, n, z_alpha)
for n in sample_sizes
for mu in true_means
}
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(mu_values, powers_n9, label="検出力 (n=9)", linestyle="--", color="blue")
plt.plot(mu_values, powers_n16, label="検出力 (n=16)", linestyle="-", color="green")
# μ = 0.4, 0.8 の場合の検出力をプロット
for (n, mu), power in specific_powers.items():
plt.scatter(mu, power, label=f"n={n}, μ={mu}, Power={power:.2f}", zorder=5)
# グラフの設定
plt.xlabel("真の平均 $\\mu$", fontsize=12)
plt.ylabel("検出力 (Power)", fontsize=12)
plt.title("検出力の挙動 ($n=9$ および $n=16$ の場合)", fontsize=14)
plt.axhline(y=alpha, color="red", linestyle=":", label=f"有意水準 α={alpha}")
plt.legend()
plt.grid(True)
plt.show()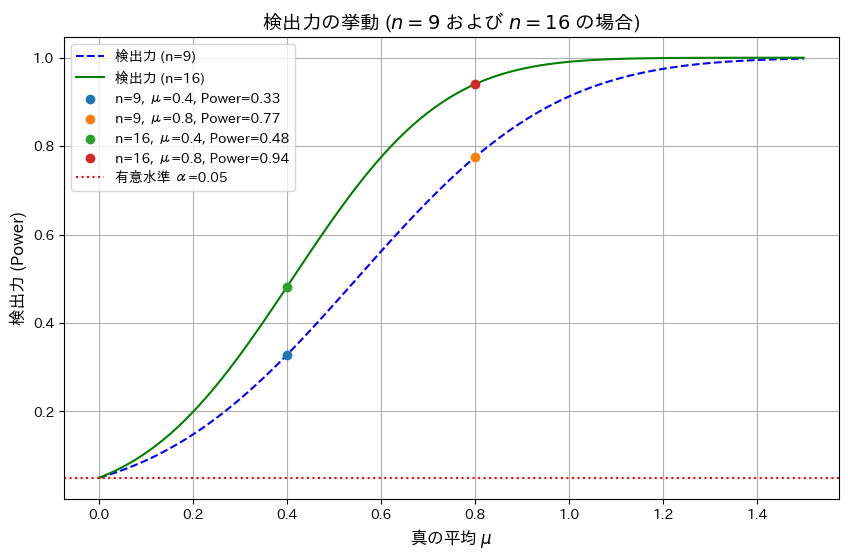
シミュレーションの結果、サンプルサイズnが増加することで検出力が向上することと、真の平均μが大きくなるほど検出力が1に近づくことが分かりました。
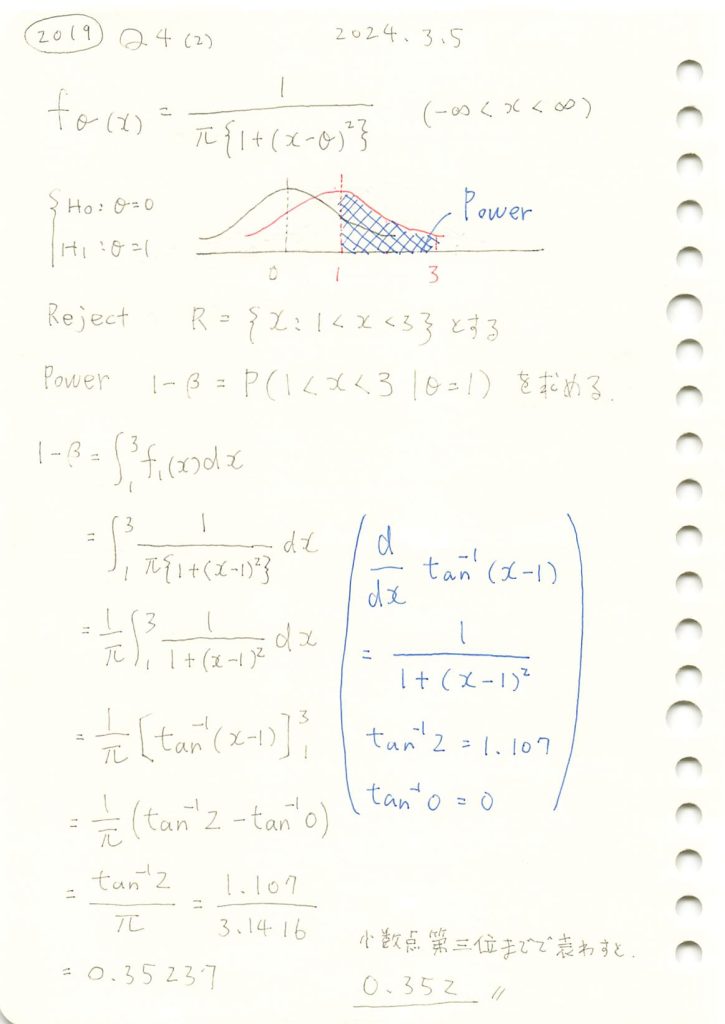
2019 Q4(2)
コーシー分布の検出力を計算しました。
コード
数式を使って検出力1-βを求めます。
# 2019 Q4(2) 2024.9.24
import numpy as np
from scipy.integrate import quad
# コーシー分布の確率密度関数 (theta = 1)
def cauchy_pdf_theta_1(x):
return 1 / (np.pi * (1 + (x - 1)**2))
# 積分範囲(棄却域R = (1, 3))
lower_bound = 1
upper_bound = 3
# 積分を実行
power, error = quad(cauchy_pdf_theta_1, lower_bound, upper_bound)
# 結果を表示(小数第3位まで表示)
print(f"検出力 (1 - β): {power:.3f}")検出力 (1 - β): 0.352手計算と一致しました。
次に、数値シミュレーションで計算をしてみます。なお、コーシー分布は裾が重いため-8 ~8の範囲になるようにフィルターを掛けることにします。
# 2019 Q4(2) 2024.9.24
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import cauchy
# シミュレーションのパラメータ
np.random.seed(43)
num_trials = 100000
# 棄却域 R = (1, 3)
lower_bound = 1
upper_bound = 3
# コーシー分布 (θ = 1) からのサンプルを生成
samples = cauchy.rvs(loc=1, scale=1, size=num_trials)
# -8 から 8 の範囲にサンプルを制限して外れ値を除外
filtered_samples = samples[(samples > -8) & (samples < 8)]
# 棄却域に入っているかどうかを判定
reject = (samples > lower_bound) & (samples < upper_bound)
# 棄却域に入った割合が検出力 (1 - β)
power_simulated = np.mean(reject)
# 結果を表示
print(f"シミュレーションによる検出力 (1 - β): {power_simulated:.3f}")
# ヒストグラムのプロット(フィルタリングしたサンプルを使う)
plt.figure(figsize=(10, 6))
plt.hist(filtered_samples, bins=100, density=True, alpha=0.5, color='blue', label='シミュレーション結果(フィルタリング済み)')
# 理論的なコーシー分布の確率密度関数 (theta = 1) をプロット
x = np.linspace(-8, 8, 1000)
pdf_theta_1 = cauchy.pdf(x, loc=1) # 対立仮説の理論曲線 (θ = 1)
plt.plot(x, pdf_theta_1, 'r-', lw=2, label='理論的コーシー分布 (θ = 1)')
# 理論的なコーシー分布の確率密度関数 (theta = 0) をプロット
pdf_theta_0 = cauchy.pdf(x, loc=0) # 帰無仮説の理論曲線 (θ = 0)
plt.plot(x, pdf_theta_0, 'g--', lw=2, label='理論的コーシー分布 (θ = 0)')
# 棄却域を塗りつぶす
plt.axvspan(lower_bound, upper_bound, color='red', alpha=0.3, label='棄却域 (1 < x < 3)')
# グラフの設定
plt.xlim(-8, 8)
plt.xlabel('x')
plt.ylabel('密度')
plt.title(f'コーシー分布のシミュレーションと棄却域\nシミュレーションによる検出力 (1 - β) = {power_simulated:.3f}')
plt.legend()
plt.grid(True)
# グラフを表示
plt.show()シミュレーションによる検出力 (1 - β): 0.355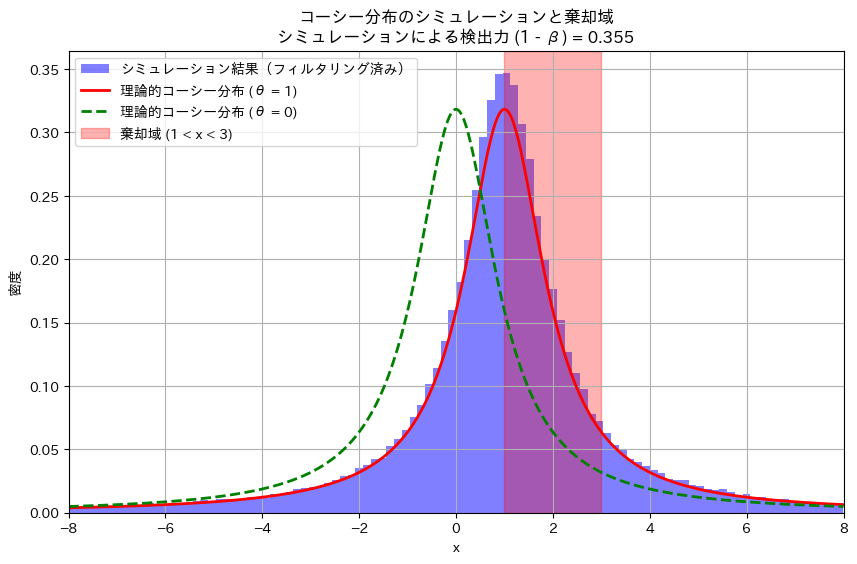
シミュレーション結果も手計算とほぼ一致しました。