ホーム » 順序統計量
「順序統計量」カテゴリーアーカイブ
2014 Q2(5)
n個の一様分布の順序統計量の期待値を求めました。
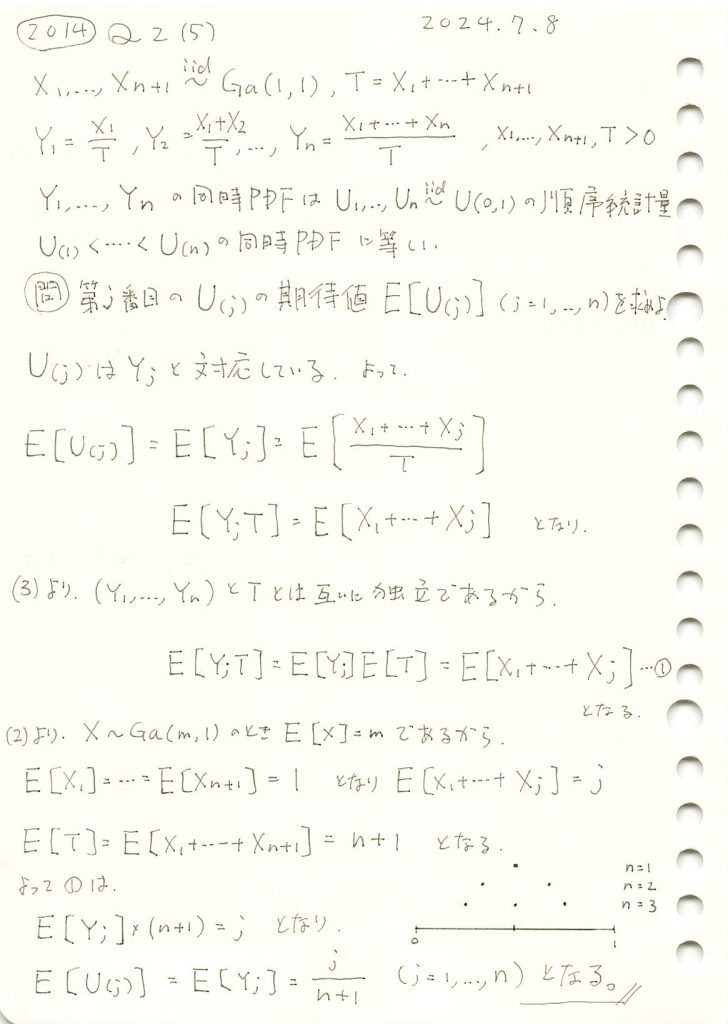
コード
サンプルサイズn=5として、一様分布の順序統計量![]() をシミュレーションし、その確率密度の形状を確認するとともに、期待値がどのようになるか確かめます。
をシミュレーションし、その確率密度の形状を確認するとともに、期待値がどのようになるか確かめます。
# 2014 Q2(5) 2024.1.4
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
n_simulations = 10**6 # サンプルサイズ
n = 5 # サンプルサイズ (n個の確率変数)
# 一様分布からサンプリング
U = np.random.uniform(0, 1, (n_simulations, n))
# PDF (確率密度関数) および期待値をプロット
j_values = range(1, n + 1) # j を 1 から n まで変化させる
plt.figure(figsize=(14, 8))
colors = ['blue', 'orange', 'green', 'red', 'purple'] # 色の設定
for idx, j in enumerate(j_values):
# j 番目の順序統計量を取得
U_j = np.sort(U, axis=1)[:, j-1]
# 理論値のPDFを計算
u = np.linspace(0, 1, 1000)
pdf_theory = (n * np.math.comb(n-1, j-1)) * (u**(j-1)) * ((1-u)**(n-j))
# ヒストグラム (シミュレーション結果)
plt.hist(U_j, bins=50, density=True, alpha=0.5, label=f'j = {j} (シミュレーション)', color=colors[idx])
# 理論値のPDFをプロット
plt.plot(u, pdf_theory, linestyle='--', color=colors[idx], label=f'j = {j} (理論)')
# 理論値の期待値を直線で追加
expected_value = j / (n + 1)
plt.axvline(x=expected_value, color=colors[idx], linestyle=':', label=f'j = {j} 期待値 = {expected_value:.2f}')
# グラフ装飾
plt.title('順序統計量 U_(j) の PDF と期待値 (理論 vs シミュレーション)', fontsize=16)
plt.xlabel('値', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()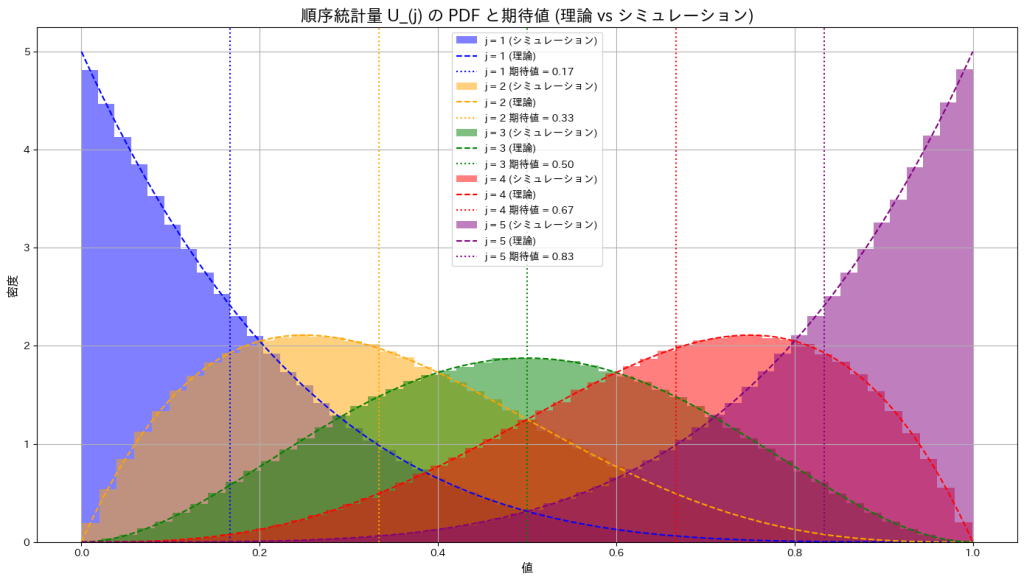
一様分布の順序統計量![]() の確率密度は、jが小さいときには左に寄り、jが大きくなると右に寄る形状を示します。また期待値はj/(n+1)であるため0~1の範囲をn+1で均等に分割した値に一致することが確認できました。
の確率密度は、jが小さいときには左に寄り、jが大きくなると右に寄る形状を示します。また期待値はj/(n+1)であるため0~1の範囲をn+1で均等に分割した値に一致することが確認できました。
2014 Q2(4)
n個の一様分布の順序統計量の同時分布が、前問の分布に等しい事を示しました。

コード
![]() と
と![]() の個別の分布をシミュレーションし、グラフを描画してみます。
の個別の分布をシミュレーションし、グラフを描画してみます。
# 2014 Q2(4) 2025.1.3
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 5 # 次元数
num_samples = 10000 # サンプル数
# (1) ガンマ分布からサンプルを生成して X_1, ..., X_(n+1) を計算
X = np.random.gamma(shape=1, scale=1, size=(num_samples, n+1)) # ガンマ分布からサンプル生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_(n+1)
# (2) Y_1, ..., Y_n を計算 (累積和を利用)
cumulative_sum_X = np.cumsum(X[:, :-1], axis=1) # 累積和 (X_1, X_1 + X_2, ..., X_1 + ... + X_n)
Y = cumulative_sum_X / T[:, None] # Y_i = (X_1 + ... + X_i) / T
# (3) 一様分布から順序統計量を生成
U = np.sort(np.random.uniform(0, 1, size=(num_samples, n)), axis=1) # 順序統計量 U_(1), ..., U_(n)
# (4) 個別の分布を比較
plt.figure(figsize=(12, 6))
for i in range(n):
plt.hist(Y[:, i], bins=50, alpha=0.5, density=True, label=rf"$Y_{i+1}$", histtype='step', linewidth=2)
plt.hist(U[:, i], bins=50, alpha=0.5, density=True, label=rf"$U_{{({i+1})}}$", histtype='step', linestyle='--', linewidth=2)
# グラフの装飾
plt.title("累積比率と順序統計量の個別分布の比較", fontsize=16)
plt.xlabel("値", fontsize=14)
plt.ylabel("確率密度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()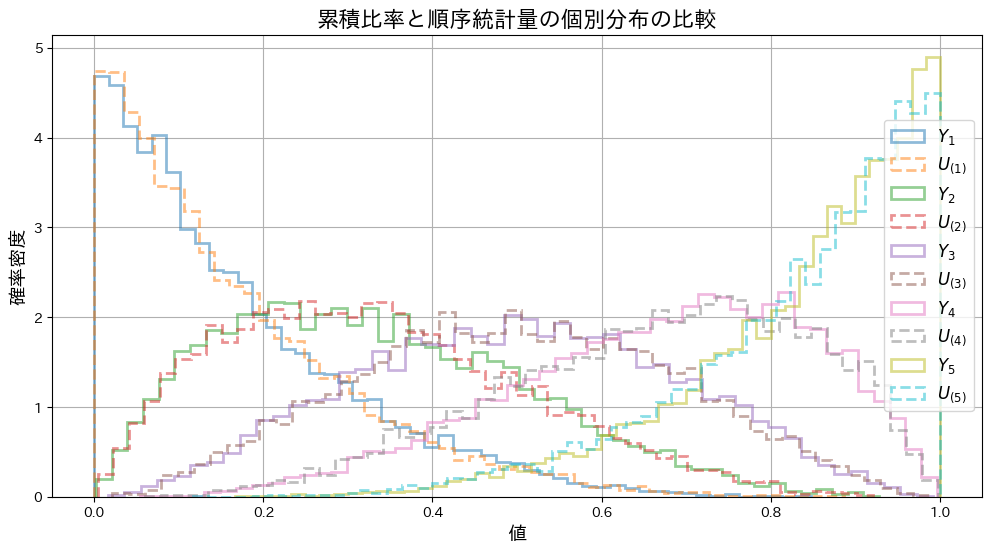
![]() と
と![]() の分布の形状は重なり、一致していることが確認できました。
の分布の形状は重なり、一致していることが確認できました。
次に、同時確率![]() と
と![]() の分布をシミュレーションし、グラフを描画してみます。
の分布をシミュレーションし、グラフを描画してみます。
# 2014 Q2(4) 2025.1.3
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 5 # 次元数
num_samples = 10000 # サンプル数
# (1) ガンマ分布からサンプルを生成して X_1, ..., X_(n+1) を計算
X = np.random.gamma(shape=1, scale=1, size=(num_samples, n+1)) # ガンマ分布からサンプル生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_(n+1)
# (2) Y_1, ..., Y_n を計算 (累積和を利用)
cumulative_sum_X = np.cumsum(X[:, :-1], axis=1) # 累積和 (X_1, X_1 + X_2, ..., X_1 + ... + X_n)
Y = cumulative_sum_X / T[:, None] # Y_i = (X_1 + ... + X_i) / T
# (3) 一様分布から順序統計量を生成
U = np.sort(np.random.uniform(0, 1, size=(num_samples, n)), axis=1) # 順序統計量 U_(1), ..., U_(n)
# (4) 同時確率密度を計算
cumulative_density = np.prod(Y, axis=1) # 累積比率 (Y_1 * Y_2 * ... * Y_n)
order_stats_density = np.prod(U, axis=1) # 順序統計量 (U_(1) * U_(2) * ... * U_(n))
# (5) ヒストグラムを描画して比較
plt.figure(figsize=(12, 6))
# 累積比率分布の同時確率密度
plt.hist(cumulative_density, bins=50, alpha=0.5, density=True, label=r"$f_Y(Y_1, Y_2, \ldots, Y_n)$")
# 順序統計量の同時確率密度
plt.hist(order_stats_density, bins=50, alpha=0.5, density=True, label=r"$f_U(U_{(1)}, U_{(2)}, \ldots, U_{(n)})$")
# グラフの装飾
plt.title("累積比率分布と順序統計量の同時確率密度の比較", fontsize=16)
plt.xlabel("同時確率密度", fontsize=14)
plt.ylabel("頻度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()
同時確率![]() と
と![]() の分布の形状は重なり、一致していることが確認できました。
の分布の形状は重なり、一致していることが確認できました。
2018 Q5(3)
一様分布の3つの順序統計量のうち第3と第1の確率変数の差の期待値と分散を求めました。
コード
同時確率密度関数f13(y1,y3)を視覚化してみます。またzが一定になる線も描画してみます。
# 2018 Q5(3) 2024.10.23
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 定義域 (y1 と y3 は [0, 1] の範囲で変動)
y1_values = np.linspace(0, 1, 100)
y3_values = np.linspace(0, 1, 100)
# メッシュグリッドを作成
Y1, Y3 = np.meshgrid(y1_values, y3_values)
# 同時確率密度関数 f13(y1, y3) = 6(y3 - y1), ただし y3 >= y1
f13 = np.where(Y3 >= Y1, 6 * (Y3 - Y1), 0)
# 等高線のための Z の値を設定 (例として Z = 0.2, 0.5, 0.8 を使用)
Z_values = [0.2, 0.5, 0.8]
# 3D グラフの描画を再度行う
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 3Dプロット (同時確率密度関数 f13(y1, y3))
ax.plot_surface(Y1, Y3, f13, cmap='viridis', alpha=0.8)
# 各 Z = Y3 - Y1 の線をプロット
for z_value in Z_values:
y1_line = np.linspace(0, 1 - z_value, 100)
y3_line = y1_line + z_value
ax.plot(y1_line, y3_line, zs=0, zdir='z', label=f'$Z = {z_value}$', lw=2)
# 軸ラベル
ax.set_title('同時確率密度関数 $f_{13}(y_1, y_3)$ と $Z = Y_3 - Y_1$', fontsize=14)
ax.set_xlabel('$y_1$', fontsize=12)
ax.set_ylabel('$y_3$', fontsize=12)
ax.set_zlabel('$f_{13}(y_1, y_3)$', fontsize=12)
# 凡例
ax.legend()
# グラフの表示
plt.show()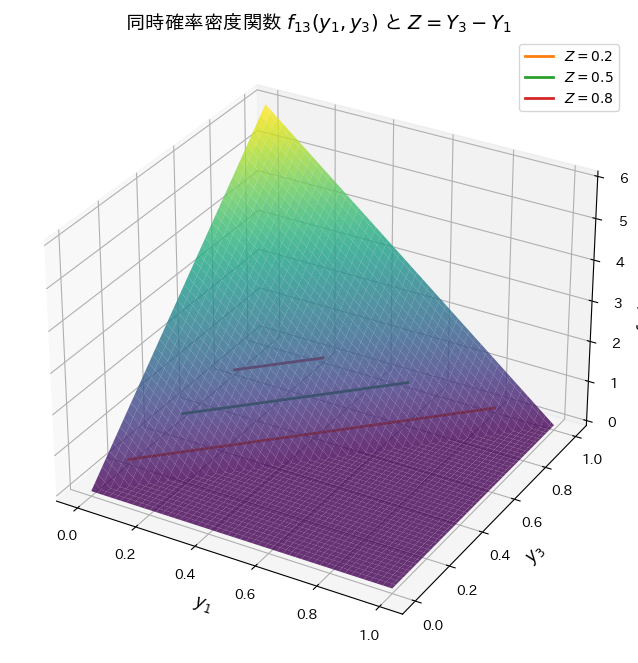
Z=z で垂直に切った断面の面積が![]() に相当します。
に相当します。
![]() を解いてZの確率密度関数を
を解いてZの確率密度関数を![]() のように求めます。順序統計量Y1とY3をシミュレーションし、理論と一致するか確認します。
のように求めます。順序統計量Y1とY3をシミュレーションし、理論と一致するか確認します。
# 2018 Q5(3) 2024.10.23
import numpy as np
import matplotlib.pyplot as plt
# サンプルデータの生成 (Z = Y3 - Y1 としてシミュレーション)
n_samples = 10000 # サンプル数
samples = np.random.uniform(0, 1, (n_samples, 3)) # 一様分布からサンプリング
Y1_samples = np.min(samples, axis=1) # 最小値 Y1
Y3_samples = np.max(samples, axis=1) # 最大値 Y3
# Z = Y3 - Y1 を計算
Z_samples = Y3_samples - Y1_samples
# Zの期待値と分散を計算
expected_Z = np.mean(Z_samples)
variance_Z = np.var(Z_samples)
# 理論値との比較
theoretical_Z_mean = 0.5
theoretical_Z_var = 1/20
# 期待値と分散を表示
print(f"シミュレーションによる E[Z](期待値): {expected_Z:.4f}, 理論値: {theoretical_Z_mean:.4f}")
print(f"シミュレーションによる Var[Z](分散): {variance_Z:.4f}, 理論値: {theoretical_Z_var:.4f}")
# Zの理論的な確率密度関数の定義
z_values = np.linspace(0, 1, 500)
f_z_theoretical = 6 * z_values * (1 - z_values)
# ヒストグラムと理論的なPDFを重ねて描画
plt.figure(figsize=(8, 6))
# サンプルのヒストグラムを描画 (確率密度として正規化)
plt.hist(Z_samples, bins=50, density=True, alpha=0.5, color='purple', label='Z samples (Y3 - Y1)')
# 理論的な確率密度関数のプロット
plt.plot(z_values, f_z_theoretical, label='Theoretical $f_Z(z) = 6z(1-z)$', color='black', linewidth=2)
# グラフの設定
plt.title('Z = Y3 - Y1 の確率密度関数 (シミュレーションと理論)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Z](期待値): 0.4992, 理論値: 0.5000
シミュレーションによる Var[Z](分散): 0.0500, 理論値: 0.0500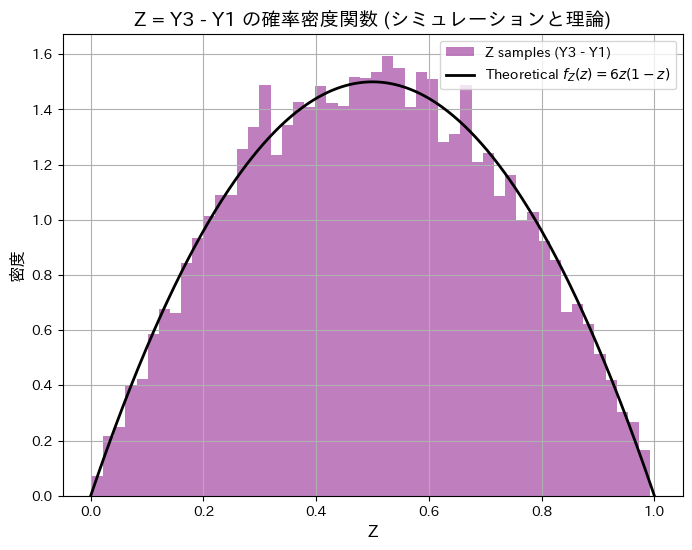
シミュレーションによる順序統計量Y3とY1の差の分布と期待値と分散が理論値と一致しました。
また興味深いことに、ZとY2は同じ分布になっていることが分かりました。
2018 Q5(2)
一様分布の3つの順序統計量のうち真ん中の確率密度関数と確率の計算をしました。
コード
シミュレーションにより順序統計量Y2の分布と期待値が理論値と一致するか確認します。
# 2018 Q5(2) 2024.10.22
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数 f2(y) の定義
f2_y = 6 * y_values * (1 - y_values)
# シミュレーションの設定
n_samples = 10000 # サンプル数
# 一様分布から3つの変数をサンプリング
samples = np.random.uniform(0, 1, (n_samples, 3))
# 順序統計量の第2要素を抽出 (Y2)
Y2_samples = np.median(samples, axis=1) # 中央値
# 期待値の計算
expected_Y2 = np.mean(Y2_samples)
# 理論値との比較
theoretical_Y2 = 0.5 # 中央値
# 期待値を表示
print(f"シミュレーションによる E[Y2](中間値の期待値): {expected_Y2:.4f}, 理論値: {theoretical_Y2:.4f}")
# ヒストグラムの作成
plt.figure(figsize=(8, 6))
# 理論密度関数 f2(y) のプロット
plt.plot(y_values, f2_y, label='$f_2(y) = 6y(1-y)$', color='red')
# サンプルのヒストグラムを追加 (確率密度として正規化)
plt.hist(Y2_samples, bins=50, density=True, alpha=0.5, color='red', label='Y2 samples (median)')
# グラフの設定
plt.title('確率密度関数 $f_2(y)$ とヒストグラム (シミュレーションと理論)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Y2](中間値の期待値): 0.5006, 理論値: 0.5000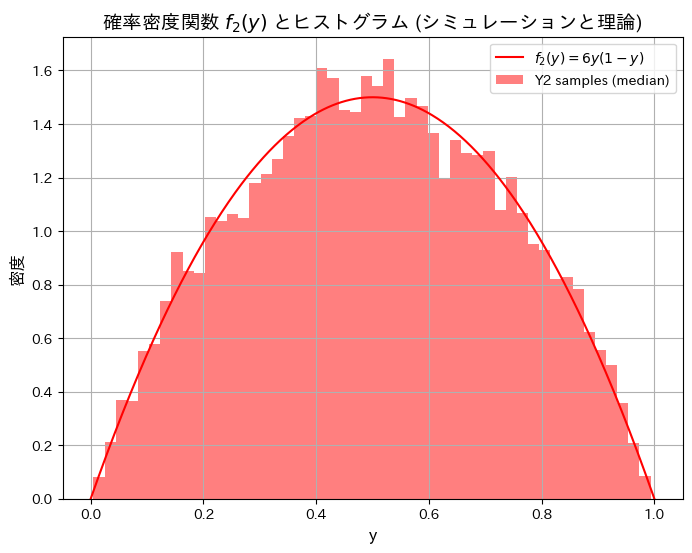
シミュレーションによる順序統計量Y1とY3の分布と期待値が理論値と一致しました。
次に、Y1~Y3の確率密度関数と累積分布関数を重ねて見てみます。
# 2018 Q5(2) 2024.10.22
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数の定義
f1_y = 3 * (1 - y_values) ** 2
f2_y = 6 * y_values * (1 - y_values)
f3_y = 3 * y_values ** 2
# CDF (累積分布関数) の計算
cdf1_y = np.cumsum(f1_y) * (y_values[1] - y_values[0])
cdf2_y = np.cumsum(f2_y) * (y_values[1] - y_values[0])
cdf3_y = np.cumsum(f3_y) * (y_values[1] - y_values[0])
# グラフの作成
plt.figure(figsize=(10, 8))
# 確率密度関数 (PDF) のプロット
plt.subplot(2, 1, 1)
plt.plot(y_values, f1_y, label='$f_1(y)$', color='blue')
plt.plot(y_values, f2_y, label='$f_2(y)$', color='red')
plt.plot(y_values, f3_y, label='$f_3(y)$', color='green')
plt.title('確率密度関数 (PDF)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# 累積分布関数 (CDF) のプロット
plt.subplot(2, 1, 2)
plt.plot(y_values, cdf1_y, label='$F_1(y)$', color='blue')
plt.plot(y_values, cdf2_y, label='$F_2(y)$', color='red')
plt.plot(y_values, cdf3_y, label='$F_3(y)$', color='green')
plt.title('累積分布関数 (CDF)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('累積確率', fontsize=12)
plt.legend(loc='lower right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()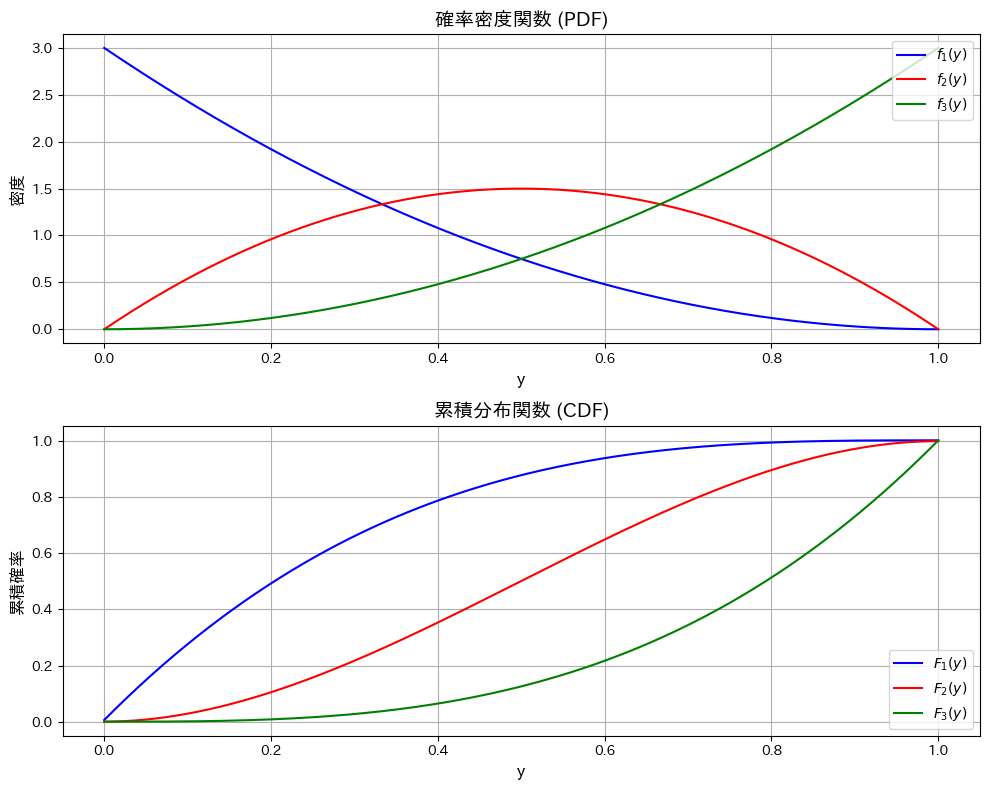
Y1は左寄り、Y2は中央寄り、Y3は右寄りになっていて、順序統計量の性質を直感的に表されています。Y2の確率密度関数は左右対称なので期待値が0.5になることも分かります。Y2の累積分布関数が直線でないことも面白いです。
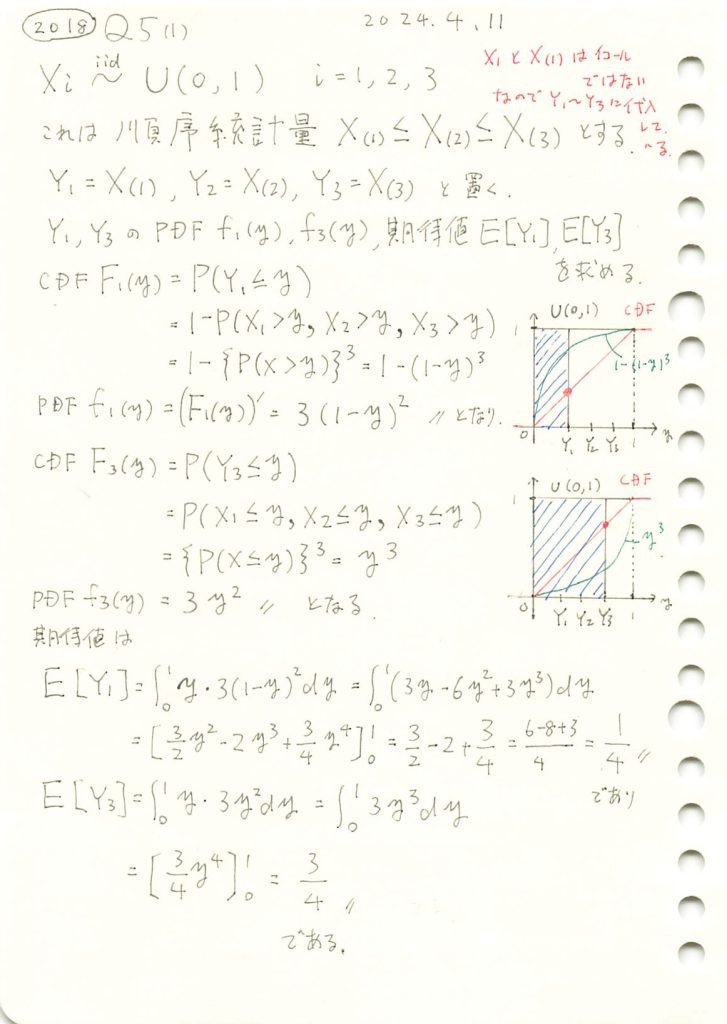
2018 Q5(1)
一様分布の順序統計量の確率密度関数と期待値を求めました。
コード
シミュレーションにより順序統計量Y1とY3の分布と期待値が理論値と一致するか確認します。
# 2018 Q5(1) 2024.10.21
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数の定義
f1_y = 3 * (1 - y_values) ** 2
f3_y = 3 * y_values ** 2
# シミュレーションの設定
n_samples = 10000 # サンプル数
# 一様分布から3つの変数をサンプリング
samples = np.random.uniform(0, 1, (n_samples, 3))
# 順序統計量を求める
Y1_samples = np.min(samples, axis=1) # 最小値
Y3_samples = np.max(samples, axis=1) # 最大値
# 期待値の計算
expected_Y1 = np.mean(Y1_samples)
expected_Y3 = np.mean(Y3_samples)
# 理論値との比較
theoretical_Y1 = 1/4
theoretical_Y3 = 3/4
# 期待値を表示
print(f"シミュレーションによる E[Y1](最小値の期待値): {expected_Y1:.4f}, 理論値: {theoretical_Y1:.4f}")
print(f"シミュレーションによる E[Y3](最大値の期待値): {expected_Y3:.4f}, 理論値: {theoretical_Y3:.4f}")
# ヒストグラムの作成
plt.figure(figsize=(8, 6))
# 理論密度関数のプロット
plt.plot(y_values, f1_y, label='$f_1(y) = 3(1-y)^2$', color='blue')
plt.plot(y_values, f3_y, label='$f_3(y) = 3y^2$', color='green')
# サンプルのヒストグラムを追加 (確率密度として正規化)
plt.hist(Y1_samples, bins=50, density=True, alpha=0.5, color='blue', label='Y1 samples (min)')
plt.hist(Y3_samples, bins=50, density=True, alpha=0.5, color='green', label='Y3 samples (max)')
# グラフの設定
plt.title('確率密度関数 $f_1(y)$ と $f_3(y)$ (シミュレーションと理論)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Y1](最小値の期待値): 0.2499, 理論値: 0.2500
シミュレーションによる E[Y3](最大値の期待値): 0.7487, 理論値: 0.7500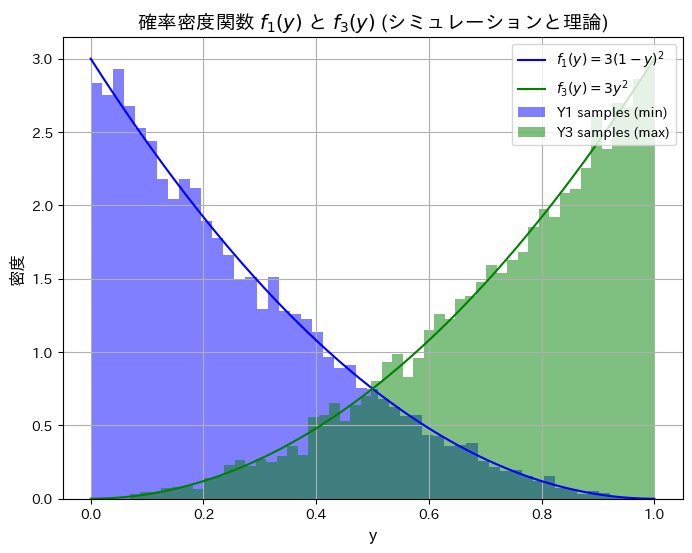
シミュレーションによる順序統計量Y1とY3の分布と期待値が理論値と一致しました。