ホーム » 平均二乗誤差MSE (ページ 2)
「平均二乗誤差MSE」カテゴリーアーカイブ
2016 Q3(2)
線形モデルの未知の母数βの最小二乗推定量を求め、それが不偏推定量であることを確認しました。
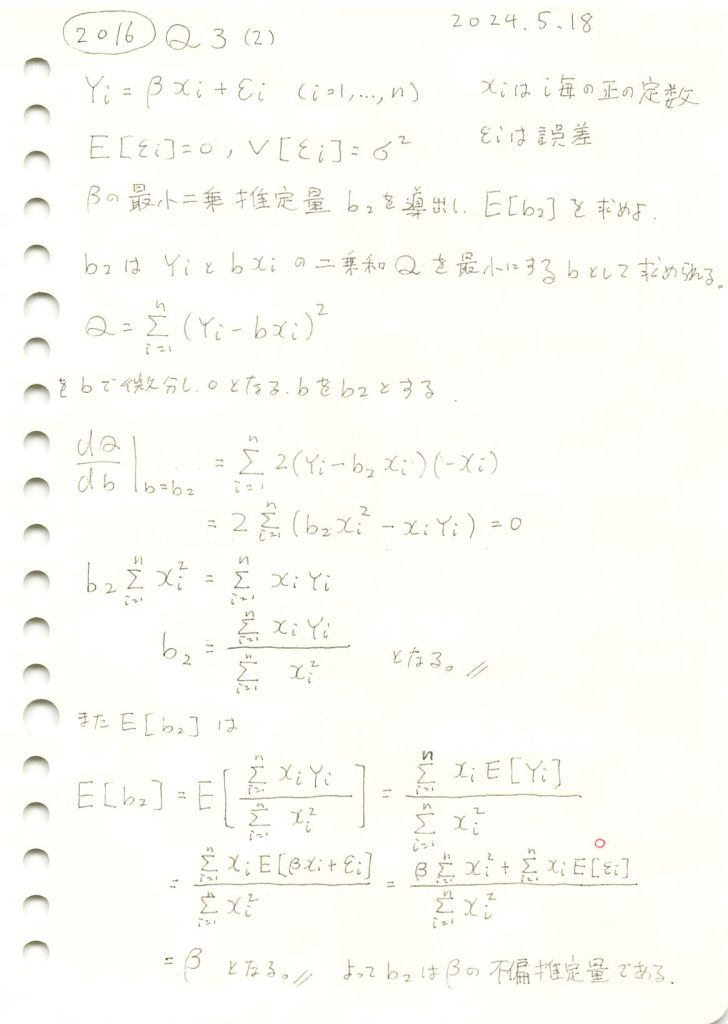
コード
乱数を発生させて線形モデルのパラメータβの推定量b0,b1,b2をそれぞれ計算し、観測データとともにプロットしてみます。推定された直線と真の直線がどのように異なるか視覚的に確認してみます。(b0,b1は前問参照)
# 2016 Q3(2) 2024.11.21
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 10 # サンプルサイズ
true_beta = 2 # 真のβ
sigma = 5 # 誤差の標準偏差
# 1. xi を一様分布から生成
xi = np.random.uniform(1, 10, n)
# 2. εi を正規分布から生成
epsilon_i = np.random.normal(0, sigma, n)
# 3. Yi を計算
Yi = true_beta * xi + epsilon_i
# 4. 推定量 b0, b1 を計算
b0 = np.mean(Yi / xi)
b1 = np.sum(Yi) / np.sum(xi)
# 5. 最小二乗推定量 b2 を計算
b2 = np.sum(xi * Yi) / np.sum(xi**2)
# プロット
plt.figure(figsize=(10, 6))
plt.scatter(xi, Yi, label='観測データ ($Y_i$)', color='blue', marker='x') # マーカーを 'x' に変更
plt.plot(np.sort(xi), true_beta * np.sort(xi), label=f'真の直線 ($\\beta={true_beta}$)', color='green', linestyle='dashed')
plt.plot(np.sort(xi), b0 * np.sort(xi), label=f'推定直線 ($b_0={b0:.2f}$)', color='red')
plt.plot(np.sort(xi), b1 * np.sort(xi), label=f'推定直線 ($b_1={b1:.2f}$)', color='orange')
plt.plot(np.sort(xi), b2 * np.sort(xi), label=f'推定直線 ($b_2={b2:.2f}$)', color='purple')
plt.xlabel('$x_i$')
plt.ylabel('$Y_i$')
plt.title('線形モデルの推定')
plt.legend()
plt.grid(True)
plt.show()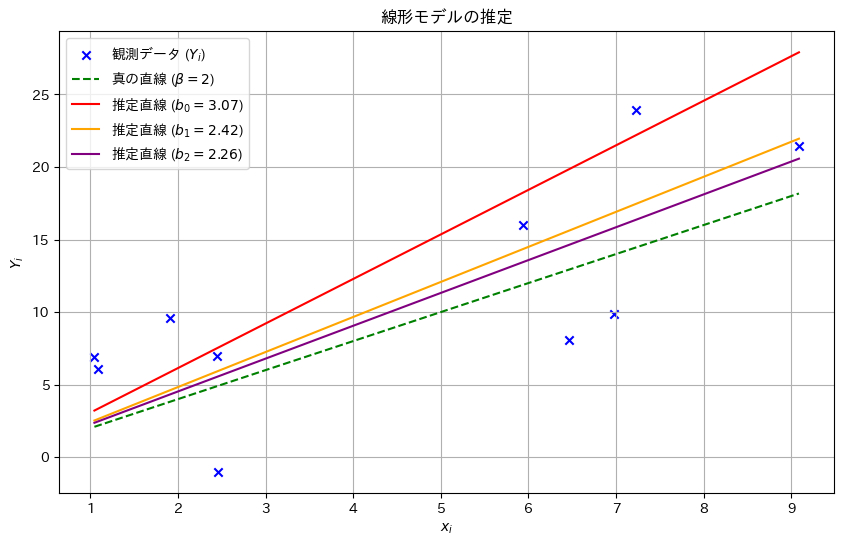
推定量b2,b1,b0の順に真のβに近い値を取りました。
次に、サンプル数nを変化させて、推定量b0,b1,b2がどのように変化するのか観察します
# 2016 Q3(2) 2024.11.21
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 5 # 誤差の標準偏差
true_beta = 2 # 真のβ
sample_sizes = np.arange(5, 101, 5) # n を 5 から 100 まで 5 刻みで変化
simulations = 1000 # 各 n に対してのシミュレーション回数
b0_means = []
b1_means = []
b2_means = [] # b2 の期待値を記録
# 各サンプルサイズ n に対してシミュレーションを実行
for n in sample_sizes:
b0_samples = []
b1_samples = []
b2_samples = [] # b2 を記録
for _ in range(simulations):
xi = np.random.uniform(1, 10, n)
epsilon_i = np.random.normal(0, sigma, n)
Yi = true_beta * xi + epsilon_i
b0_samples.append(np.mean(Yi / xi))
b1_samples.append(np.sum(Yi) / np.sum(xi))
b2_samples.append(np.sum(xi * Yi) / np.sum(xi**2)) # b2 を計算
b0_means.append(np.mean(b0_samples))
b1_means.append(np.mean(b1_samples))
b2_means.append(np.mean(b2_samples)) # b2 の期待値を記録
# 結果をプロット
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, b0_means, label='$b_0$の期待値', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, b1_means, label='$b_1$の期待値', marker='x', linestyle='dashed', color='orange')
plt.plot(sample_sizes, b2_means, label='$b_2$の期待値', marker='s', linestyle='dashed', color='purple') # b2 を追加
plt.axhline(y=true_beta, color='green', linestyle='solid', label='真の値 $\\beta=2$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('推定量の期待値')
plt.title('推定量 $b_0, b_1, b_2$ の期待値とサンプルサイズの関係')
plt.legend()
plt.grid(True)
plt.show()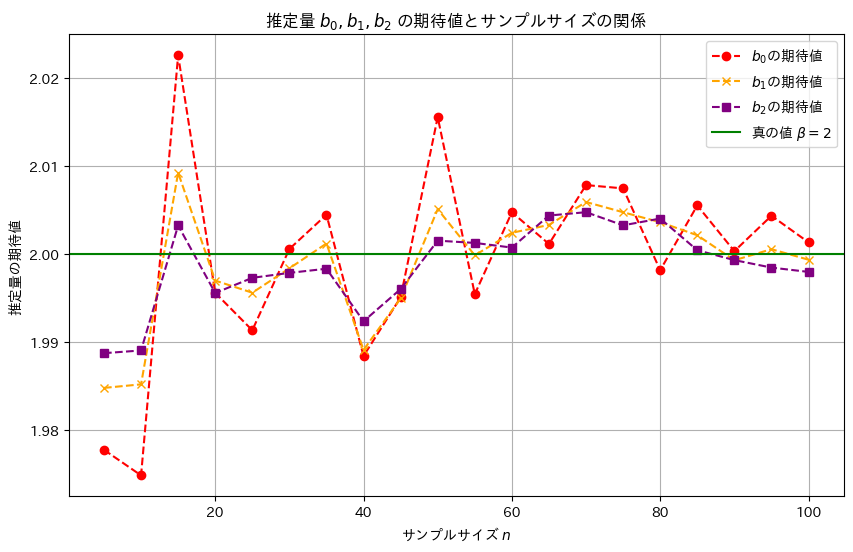
サンプルサイズnが大きくなるほど、推定量b0,b1,b2は真の値βに近づくことが確認できました。また、推定量b2,b1,b0の順に分散は小さく見え、b2,b1,b0の順により安定した推定量のようです。
次に、推定量b0,b1,b2の分布を確認してみます。それぞれのヒストグラムを重ねて表示してみます。
# 2016 Q3(2) 2024.11.21
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 100 # サンプルサイズ
true_beta = 2 # 真のβ
sigma = 1 # 誤差の標準偏差
simulations = 10000 # シミュレーション回数
b0_samples = []
b1_samples = []
b2_samples = [] # b2 の分布を記録
# シミュレーションを実施
for _ in range(simulations):
xi = np.random.uniform(1, 10, n)
epsilon_i = np.random.normal(0, sigma, n)
Yi = true_beta * xi + epsilon_i
b0_samples.append(np.mean(Yi / xi))
b1_samples.append(np.sum(Yi) / np.sum(xi))
b2_samples.append(np.sum(xi * Yi) / np.sum(xi**2)) # b2 を計算
# b0, b1, b2 の分布を重ねてプロット
plt.figure(figsize=(10, 6))
plt.hist(b0_samples, bins=30, density=True, color='red', alpha=0.5, label='$b_0$')
plt.hist(b1_samples, bins=30, density=True, color='orange', alpha=0.5, label='$b_1$')
plt.hist(b2_samples, bins=30, density=True, color='purple', alpha=0.5, label='$b_2$') # b2 を追加
plt.axvline(x=true_beta, color='green', linestyle='dashed', label='真の値 $\\beta=2$')
plt.title('$b_0$, $b_1$, $b_2$ の分布 (n=100)')
plt.xlabel('推定値')
plt.ylabel('頻度')
plt.legend()
plt.grid(True)
plt.show()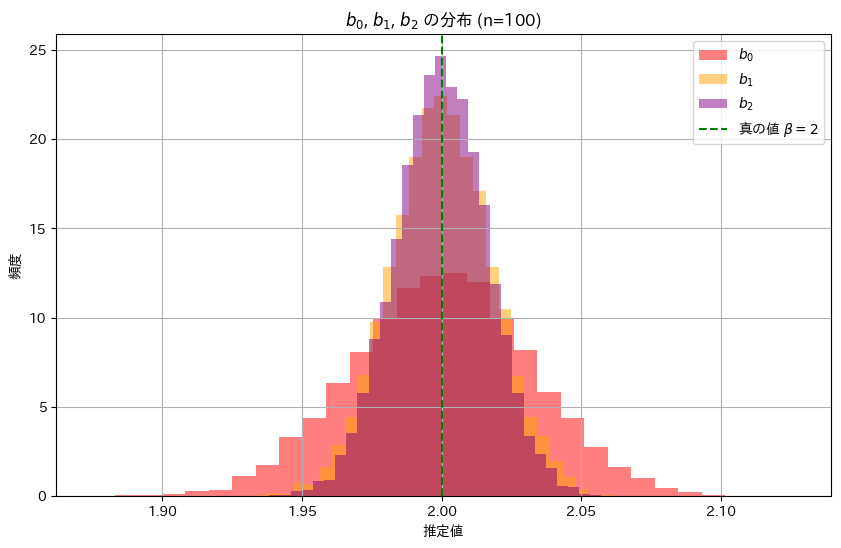
推定量b2,b1,b0の順に幅が狭く、分散が小さいことが確認できました。これにより推定量b2,b1,b0の順に安定した推定であることが分かりました。
2016 Q1(3)
正規分布の母平均μに対するθ=exp(μ)の最尤推定量の平均二乗誤差が0になることを示しました。

コード
シミュレーションを行います。![]() に対して、
に対して、![]() を計算し、理論値とともにプロットします。サンプルサイズnを増加させて、MSEの変化を観察します。
を計算し、理論値とともにプロットします。サンプルサイズnを増加させて、MSEの変化を観察します。
# 2016 Q1(3) 2024.11.13
import numpy as np
import matplotlib.pyplot as plt
# 真の値とシミュレーション設定
mu_true = 1.0 # 真の平均 (mu)
theta_true = np.exp(mu_true) # 真の θ = e^mu
n_trials = 10000 # シミュレーション試行回数
sample_sizes = np.arange(5, 101, 5) # サンプルサイズの範囲
# MSEを格納するリスト
mse_simulated = []
# 理論的なMSEの計算関数
def theoretical_mse(n, mu):
return np.exp(2 * mu) * (np.exp(2 / n) - 2 * np.exp(1 / (2 * n)) + 1)
mse_theoretical = [theoretical_mse(n, mu_true) for n in sample_sizes]
# シミュレーションでのMSE計算
for n_samples in sample_sizes:
mse_trials = []
for _ in range(n_trials):
sample = np.random.normal(loc=mu_true, scale=1, size=n_samples)
X_bar = np.mean(sample)
theta_hat = np.exp(X_bar) # 最尤推定量
mse_trials.append((theta_hat - theta_true) ** 2) # MSEの計算
mse_simulated.append(np.mean(mse_trials)) # 試行平均を格納
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, mse_simulated, marker='o', linestyle='-', color='blue', label='シミュレーション MSE')
plt.plot(sample_sizes, mse_theoretical, marker='s', linestyle='--', color='red', label='理論的 MSE')
plt.title('MSEのシミュレーションと理論値', fontsize=16)
plt.xlabel('サンプルサイズ $n$', fontsize=14)
plt.ylabel('MSE', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
plt.show()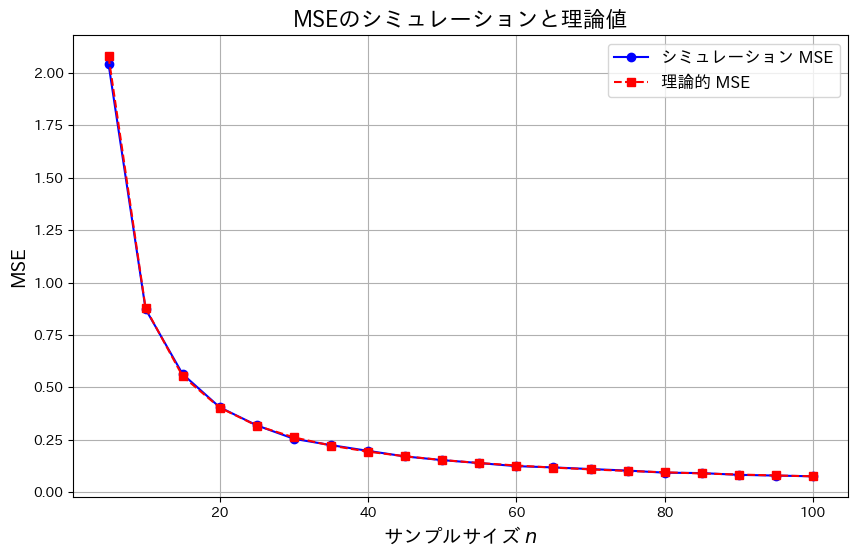
サンプルサイズnが増加するにつれて、![]() は0に近づきました。これにより、
は0に近づきました。これにより、![]() になることが理論とシミュレーションの両方で確認できました。また、この結果から最尤推定量
になることが理論とシミュレーションの両方で確認できました。また、この結果から最尤推定量 ![]() が漸近的一致性を持つことが分かりました。
が漸近的一致性を持つことが分かりました。