ホーム » モーメント
「モーメント」カテゴリーアーカイブ
2015 Q1(3)
平均周りの標本平均のk次モーメントを求めました。
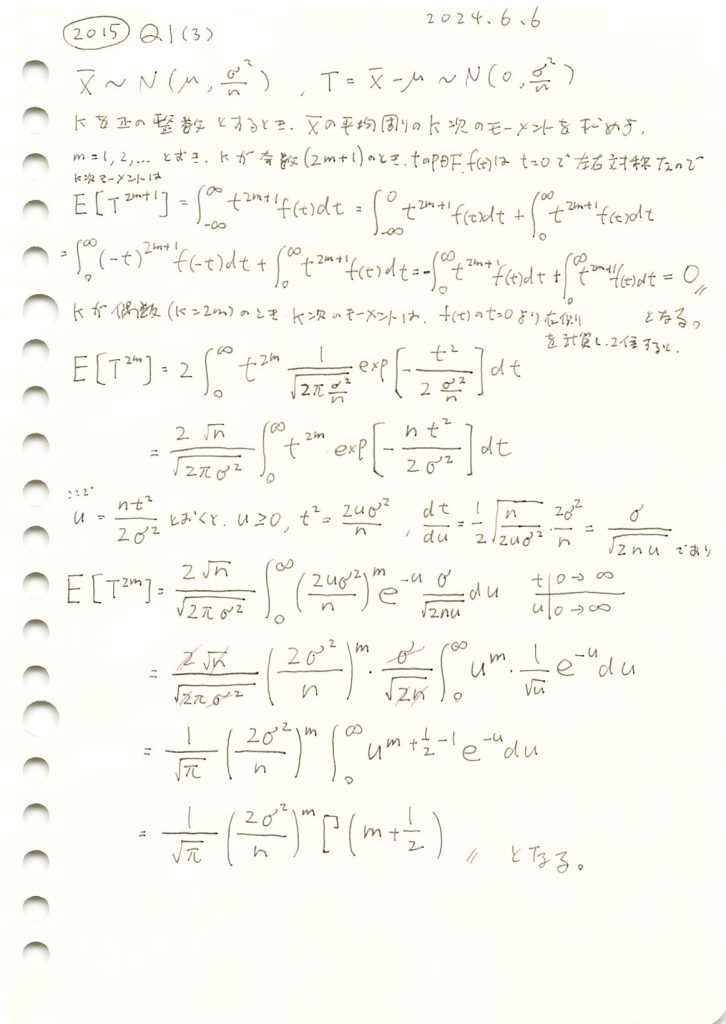
コード
![]() の平均周りのk次モーメント
の平均周りのk次モーメント![]() を、kとnを変化させてグラフの形状を確認します。
を、kとnを変化させてグラフの形状を確認します。
# 2015 Q1(3) 2024.12.4
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gamma
# パラメータ設定
sigma2 = 4 # 母分散(固定)
k_values = [2, 4, 6, 8] # 偶数次モーメント
n_values = [12, 14, 16, 18, 20] # 標本サイズ
# 理論式計算の関数
def theoretical_moment_m(m, sigma2, n):
return (gamma(m + 0.5) / np.sqrt(np.pi)) * (2 * sigma2 / n) ** m
# グラフの準備
plt.figure(figsize=(10, 6))
# 各 n に対するモーメント値を計算してプロット
for n in n_values:
moment_values = [theoretical_moment_m(k // 2, sigma2, n) for k in k_values]
plt.plot(k_values, moment_values, marker='o', linestyle='-', label=f"n={n}")
# グラフ
#plt.title(r"モーメント $\frac{\Gamma(m + 1/2)}{\sqrt{\pi}} \left(\frac{2\sigma^2}{n}\right)^m$ の形状")
plt.title(r"$\overline{X}$ の平均周りの $k$ 次モーメントの形状")
plt.xlabel(r"$k$ (偶数次モーメントの次数)")
plt.ylabel("モーメント値")
plt.xticks(k_values)
plt.grid()
plt.legend()
plt.tight_layout()
plt.show()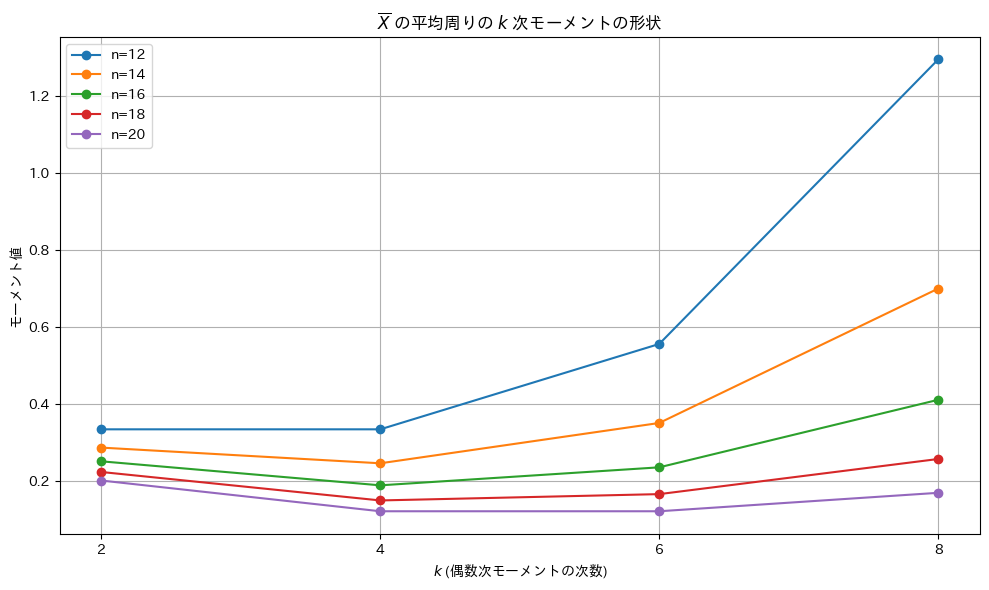
グラフの形状は谷型になっていることが確認され、特定の範囲でモーメント値が最小値を取ることがわかりました。
次に、シミュレーションを行います。標本サイズn=10の場合について実行し、理論値とシミュレーション結果が一致するかを確認します。
# 2015 Q1(3) 2024.12.4
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gamma
# パラメータ設定
mu = 0 # 母平均
sigma2 = 4 # 母分散
sigma = np.sqrt(sigma2) # 母標準偏差
n = 10 # 標本サイズ
k_values = [2, 4, 6, 8] # 偶数次モーメントを検証
num_simulations = 10000 # シミュレーション回数
# 理論値計算の関数
def theoretical_moment(k, sigma2, n):
m = k // 2
return (gamma(m + 0.5) / np.sqrt(np.pi)) * (2 * sigma2 / n) ** m
# シミュレーション値と理論値を計算
sim_results = []
theory_results = []
for k in k_values:
# シミュレーションで k 次モーメントを計算
sample_means = [np.mean(np.random.normal(mu, sigma, n)) for _ in range(num_simulations)]
k_moment_sim = np.mean([(x - mu) ** k for x in sample_means])
# 理論値を計算
k_moment_theory = theoretical_moment(k, sigma2, n)
# 保存
sim_results.append(k_moment_sim)
theory_results.append(k_moment_theory)
# 棒グラフを作成
x = np.arange(len(k_values))
width = 0.4
plt.figure(figsize=(10, 6))
# プロット
plt.bar(x - width / 2, sim_results, width, label="シミュレーション値", color='blue', alpha=0.7)
plt.bar(x + width / 2, theory_results, width, label="理論値", color='orange', alpha=0.7)
# 軸とラベル
plt.xticks(x, [f"k={k}" for k in k_values])
plt.title(f"標本サイズ n={n} におけるモーメント比較")
plt.xlabel("k 次モーメント")
plt.ylabel("モーメント値")
plt.legend()
plt.grid(axis='y')
# 表示
plt.tight_layout()
plt.show()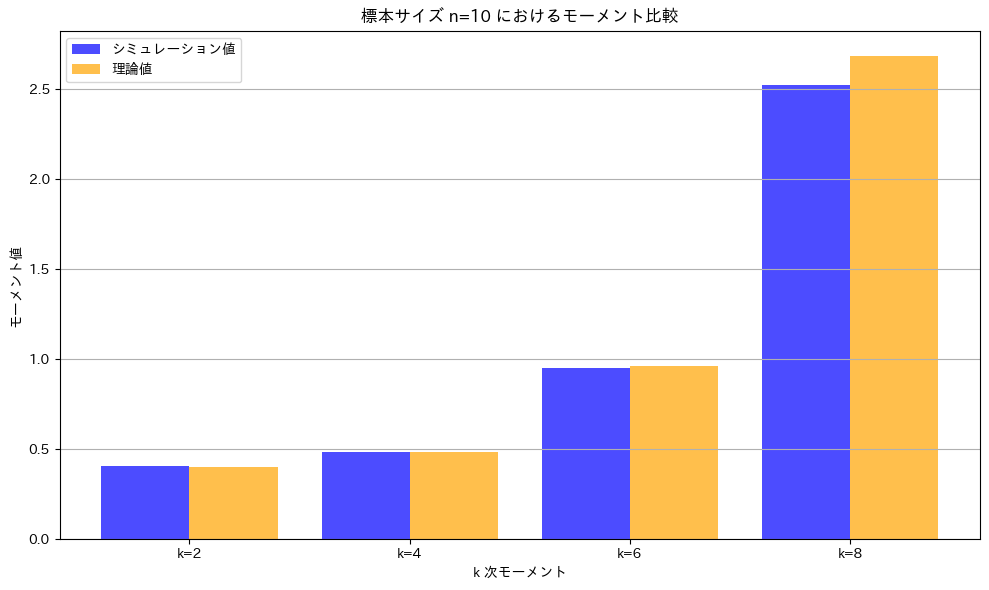
理論値とシミュレーションによる値はよく一致しています。
n=20でもう一度実行します。
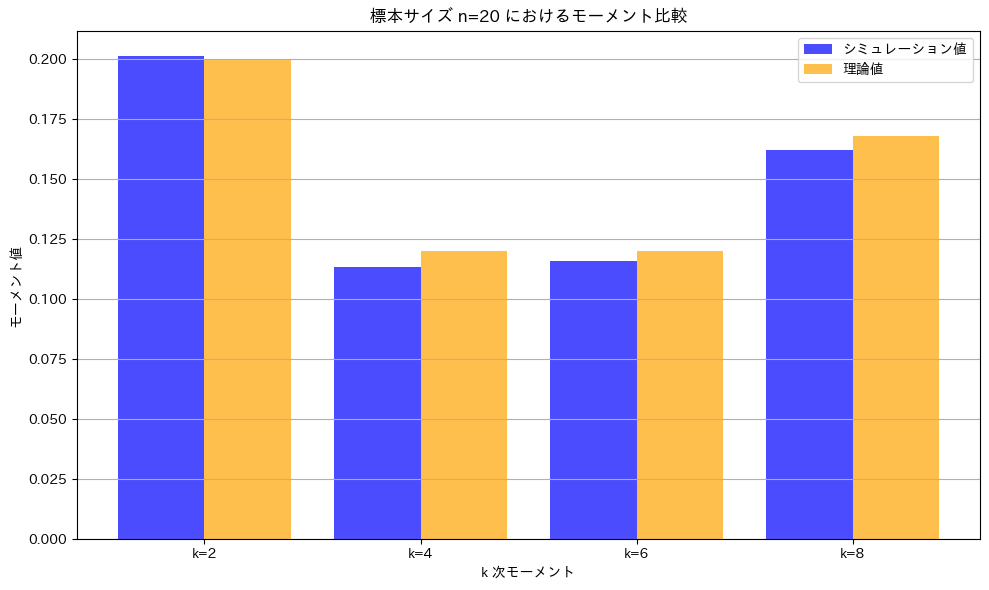
こちらもよく一致しています。グラフの形状が谷型になっていることも確認できました。