ホーム » 最尤推定
「最尤推定」カテゴリーアーカイブ
2014 Q5(1)
テレビ番組の視聴満足回数の調査で満足と答えた回数のそれぞれ人数との組みが多項分布に従うのを利用し多項確率を構成する二項分布の確率pの最尤推定量を求めました。
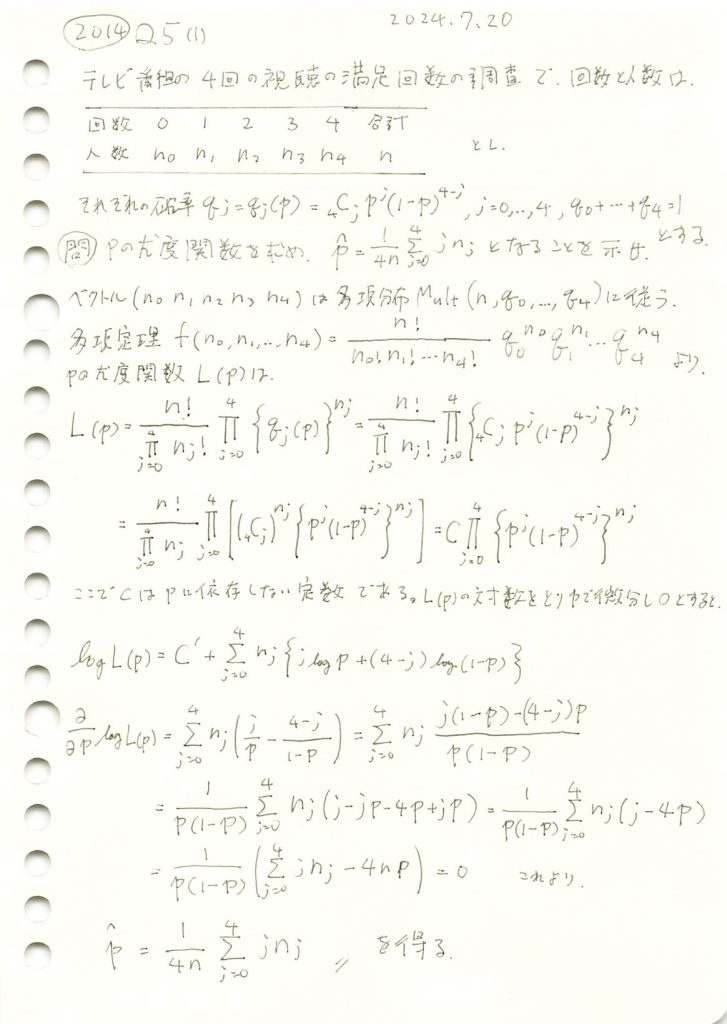
コード
真の確率pに基づいてシミュレーションを行い、最尤推定値![]() を計算し、真の確率pと比較します。
を計算し、真の確率pと比較します。
# 2014 Q5(1) 2025.1.15
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
n_simulations = 10000 # シミュレーション回数
n = 100 # 調査対象の人数
p_true = 0.6 # 真の満足確率
# nj のシミュレーション (j = 0, 1, 2, 3, 4)
data = np.random.binomial(4, p_true, size=n_simulations * n).reshape(n_simulations, n)
# 各シミュレーションでの最尤推定値を計算
p_estimates = np.sum(data, axis=1) / (4 * n)
# 平均値(推定されたp^の期待値)を計算
mean_p_estimate = np.mean(p_estimates)
# 推定されたp^の平均値と真の値を出力
print(f"推定された最尤推定値の平均: {mean_p_estimate:.4f}")
print(f"真の値: {p_true:.4f}")
# グラフの描画
plt.hist(p_estimates, bins=30, density=True, alpha=0.75, label="推定された $\\hat{p}$")
plt.axvline(p_true, color='red', linestyle='dashed', label=f"真の値 $p = {p_true}$")
plt.xlabel("推定された $\\hat{p}$")
plt.ylabel("密度")
plt.title("最尤推定値 $\\hat{p}$ の分布")
plt.legend()
plt.grid(alpha=0.5)
plt.show()推定された最尤推定値の平均: 0.5997
真の値: 0.6000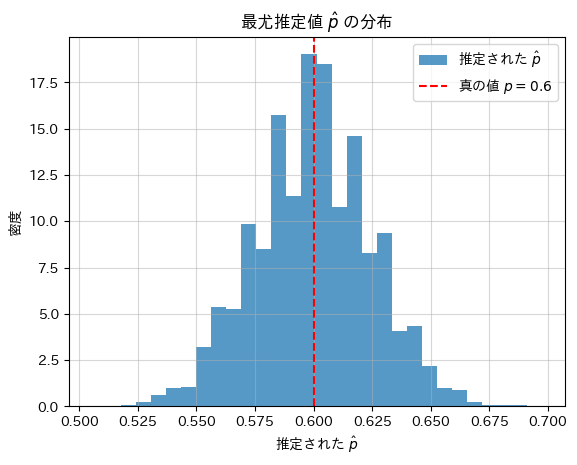
シミュレーションの結果、最尤推定値![]() は、真の確率pに近い値を示しました。
は、真の確率pに近い値を示しました。
2015 Q4(2)
確率の分割表に対称性があるという仮説の下での期待度数の最尤推定を行いました。
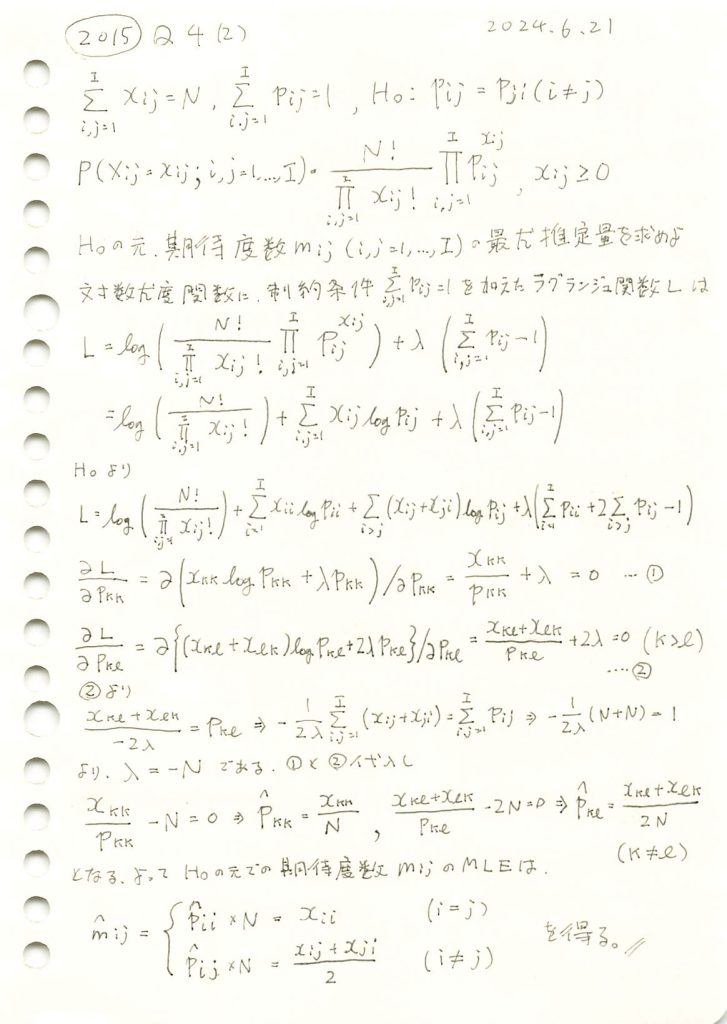
与えられた観測度数表から![]() に基づき期待度数を求めます。
に基づき期待度数を求めます。
# 2015 Q4(2) 2024.12.18
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 1. 観測度数表
observed_counts = np.array([[1520, 266, 124, 66],
[234, 1512, 432, 78],
[117, 362, 1772, 205],
[36, 82, 179, 492]])
# 2. 総サンプルサイズ N
N = observed_counts.sum()
# 3. 期待度数 m_ij の計算 (対称性の仮説)
m_ij = np.zeros_like(observed_counts, dtype=float)
I = observed_counts.shape[0]
for i in range(I):
for j in range(I):
if i == j: # 対角要素
m_ij[i, j] = observed_counts[i, j]
else: # 非対角要素
m_ij[i, j] = (observed_counts[i, j] + observed_counts[j, i]) / 2
# 4. 観測度数と期待度数をDataFrameにまとめる
row_labels = col_labels = ["Highest", "Second", "Third", "Lowest"]
df_observed = pd.DataFrame(observed_counts, index=row_labels, columns=col_labels)
df_expected = pd.DataFrame(np.round(m_ij, 2), index=row_labels, columns=col_labels)
# 5. 観測度数と期待度数のヒートマップを作成
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
# 観測度数のヒートマップ
sns.heatmap(df_observed, annot=True, fmt=".0f", cmap="Blues", ax=axes[0])
axes[0].set_title("観測度数表 $x_{ij}$")
# 期待度数のヒートマップ
sns.heatmap(df_expected, annot=True, fmt=".2f", cmap="Greens", ax=axes[1])
axes[1].set_title("期待度数表 $\hat{m}_{ij}$ (対称性の仮説)")
plt.tight_layout()
plt.show()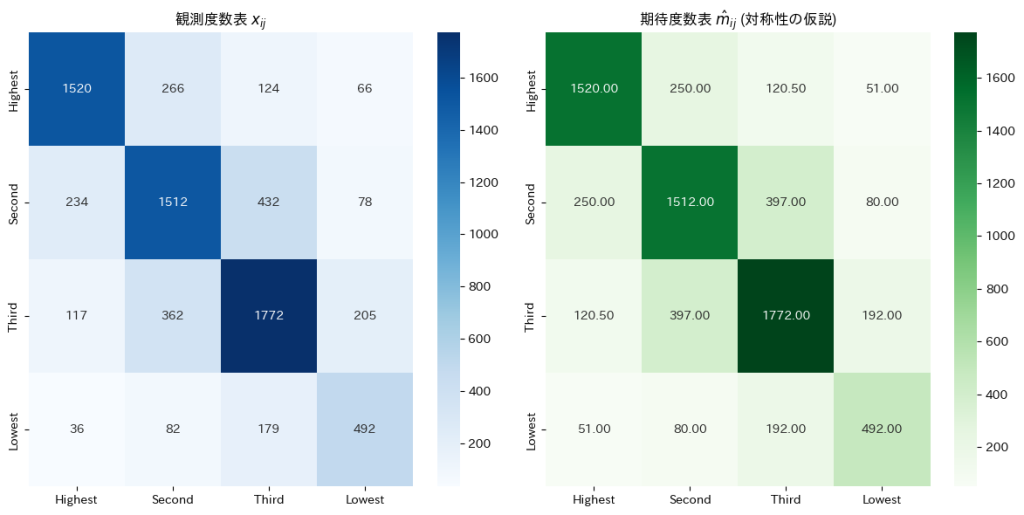
与えられた観測度数表から![]() に基づいて期待度数を求めると、非対角要素は対応する2つの観測度数の平均として表され、対角要素は観測度数そのものが期待度数となりました。
に基づいて期待度数を求めると、非対角要素は対応する2つの観測度数の平均として表され、対角要素は観測度数そのものが期待度数となりました。
2016 Q2(3)
指数分布のλと、上側α点を返す関数の最尤推定量を求め、不偏であるか確認しました。

コード
最尤推定量![]() をシミュレーションし、理論値
をシミュレーションし、理論値![]() と比較します。共にグラフに描画し、どの程度一致しているか確認します。
と比較します。共にグラフに描画し、どの程度一致しているか確認します。
# 2016 Q2(3) 2024.11.17
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
lambda_value = 2 # 真のλ
n = 100 # サンプル数
c = 1.0 # Q(c) を計算するための c の値
alpha_values = [0.1, 0.25, 0.5, 0.75, 0.9] # αの値
# 1. 指数分布からサンプルを生成
samples = np.random.exponential(scale=1/lambda_value, size=n)
# 2. λの最尤推定量を計算
lambda_hat = n / np.sum(samples)
# 3. Q(c) の最尤推定量を計算
Q_hat_c = np.exp(-lambda_hat * c)
Q_theoretical_c = np.exp(-lambda_value * c)
# 4. u(α) の最尤推定量を計算
u_hat_alpha = [-np.mean(samples) * np.log(alpha) for alpha in alpha_values]
u_theoretical_alpha = [-np.log(alpha) / lambda_value for alpha in alpha_values]
# グラフ作成部分
plt.figure(figsize=(10, 6))
# 理論値と最尤推定量の u(α) をプロット
plt.plot(alpha_values, u_theoretical_alpha, 'r-o', label='u(α) 理論値', linewidth=2)
plt.plot(alpha_values, u_hat_alpha, 'b--s', label='u(α) 最尤推定量', linewidth=2) # 'b--s' で破線とマーカーを指定
# グラフの設定
plt.title('u(α) の理論値と最尤推定量の比較', fontsize=16)
plt.xlabel('α', fontsize=14)
plt.ylabel('u(α)', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
plt.xticks(alpha_values)
# グラフの表示
plt.show()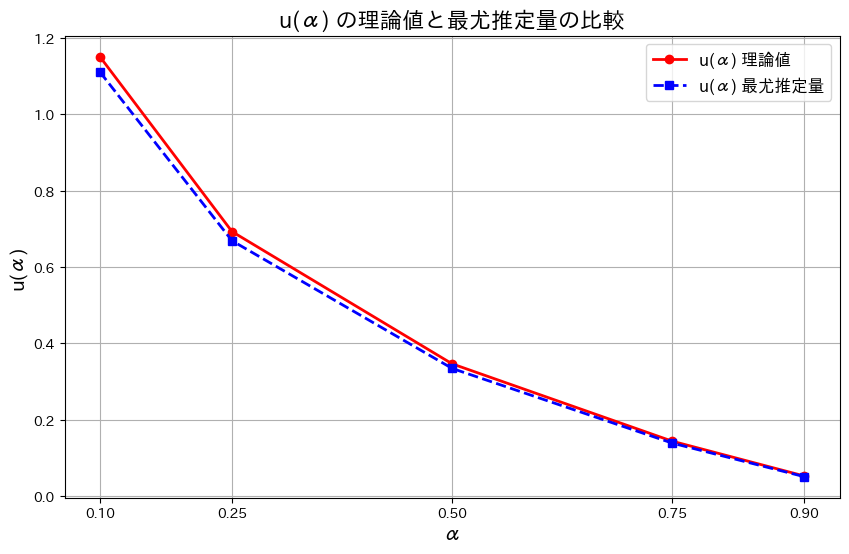
![]() はわずかに誤差があるものの概ね一致しました。また誤差はαが大きくなるにつれて小さくなります。その理由は、αが大きくなるとu(α)の値が小さくなり、分布の高密度な部分にサンプルが集中するためと考えられます。
はわずかに誤差があるものの概ね一致しました。また誤差はαが大きくなるにつれて小さくなります。その理由は、αが大きくなるとu(α)の値が小さくなり、分布の高密度な部分にサンプルが集中するためと考えられます。
2016 Q1(3)
正規分布の母平均μに対するθ=exp(μ)の最尤推定量の平均二乗誤差が0になることを示しました。

コード
シミュレーションを行います。![]() に対して、
に対して、![]() を計算し、理論値とともにプロットします。サンプルサイズnを増加させて、MSEの変化を観察します。
を計算し、理論値とともにプロットします。サンプルサイズnを増加させて、MSEの変化を観察します。
# 2016 Q1(3) 2024.11.13
import numpy as np
import matplotlib.pyplot as plt
# 真の値とシミュレーション設定
mu_true = 1.0 # 真の平均 (mu)
theta_true = np.exp(mu_true) # 真の θ = e^mu
n_trials = 10000 # シミュレーション試行回数
sample_sizes = np.arange(5, 101, 5) # サンプルサイズの範囲
# MSEを格納するリスト
mse_simulated = []
# 理論的なMSEの計算関数
def theoretical_mse(n, mu):
return np.exp(2 * mu) * (np.exp(2 / n) - 2 * np.exp(1 / (2 * n)) + 1)
mse_theoretical = [theoretical_mse(n, mu_true) for n in sample_sizes]
# シミュレーションでのMSE計算
for n_samples in sample_sizes:
mse_trials = []
for _ in range(n_trials):
sample = np.random.normal(loc=mu_true, scale=1, size=n_samples)
X_bar = np.mean(sample)
theta_hat = np.exp(X_bar) # 最尤推定量
mse_trials.append((theta_hat - theta_true) ** 2) # MSEの計算
mse_simulated.append(np.mean(mse_trials)) # 試行平均を格納
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, mse_simulated, marker='o', linestyle='-', color='blue', label='シミュレーション MSE')
plt.plot(sample_sizes, mse_theoretical, marker='s', linestyle='--', color='red', label='理論的 MSE')
plt.title('MSEのシミュレーションと理論値', fontsize=16)
plt.xlabel('サンプルサイズ $n$', fontsize=14)
plt.ylabel('MSE', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
plt.show()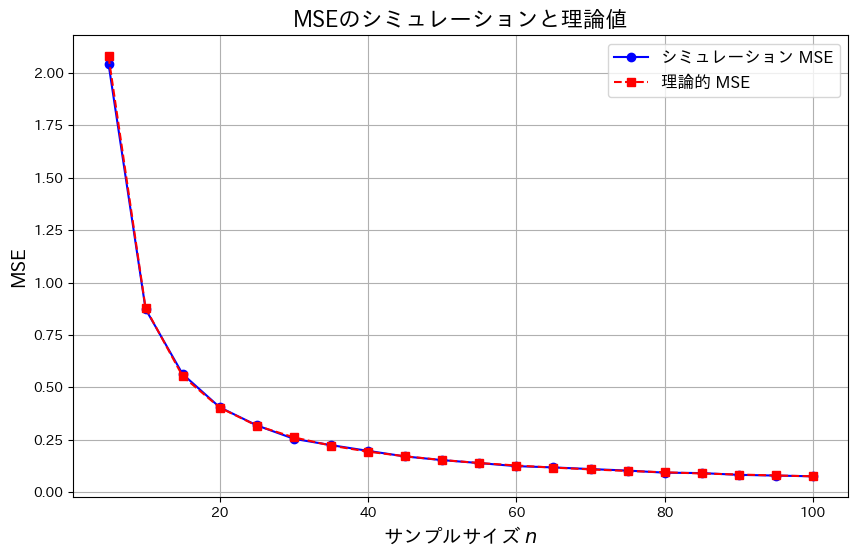
サンプルサイズnが増加するにつれて、![]() は0に近づきました。これにより、
は0に近づきました。これにより、![]() になることが理論とシミュレーションの両方で確認できました。また、この結果から最尤推定量
になることが理論とシミュレーションの両方で確認できました。また、この結果から最尤推定量 ![]() が漸近的一致性を持つことが分かりました。
が漸近的一致性を持つことが分かりました。
2016 Q1(2)
正規分布の母平均μに対してθ=exp(μ)をパラメータとする最尤推定量のバイアスを調べて、与式がθの不偏推定量であることを示しました。
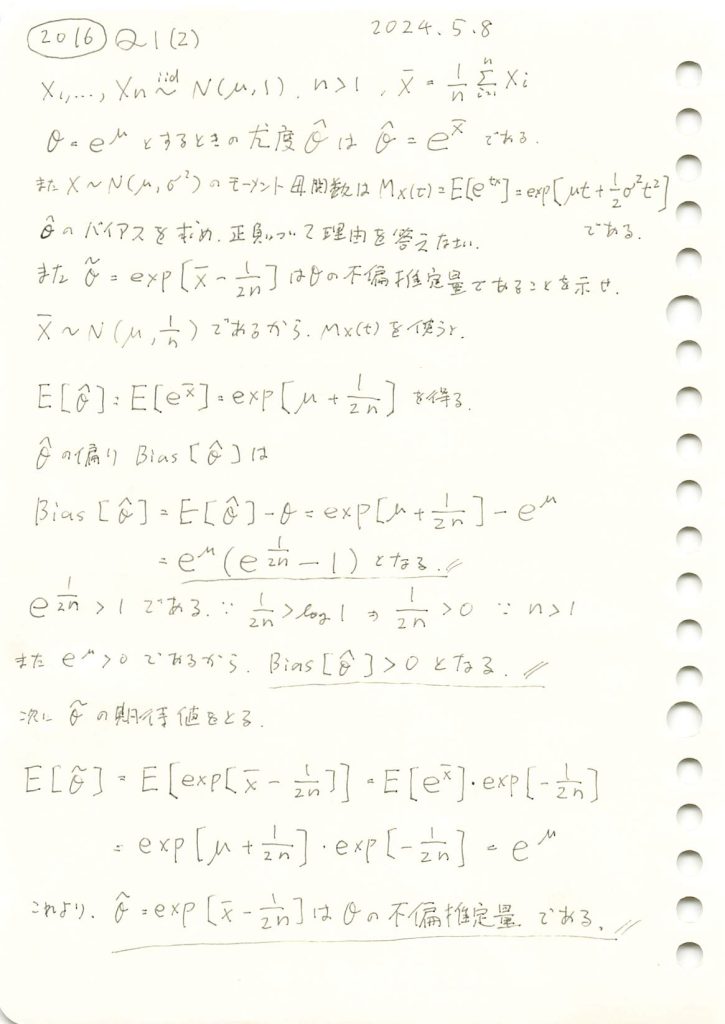
コード
![]() と
と![]() が真のθに近づくか確認するため、シミュレーションを行います。まずはサンプルサイズn=5で試してみます。
が真のθに近づくか確認するため、シミュレーションを行います。まずはサンプルサイズn=5で試してみます。
# 2016 Q1(2) 2024.11.12
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
mu_true = 1.0 # 真の平均 (mu)
theta_true = np.exp(mu_true) # 真の θ = e^mu
n_samples = 5 # サンプルサイズ
n_trials = 100000 # シミュレーション試行回数
# 乱数生成と推定量の計算
theta_hat_estimates = []
theta_tilde_estimates = []
for _ in range(n_trials):
sample = np.random.normal(loc=mu_true, scale=1/np.sqrt(n_samples), size=n_samples)
X_bar = np.mean(sample) # 標本平均
# 最尤推定量 θ^
theta_hat = np.exp(X_bar)
theta_hat_estimates.append(theta_hat)
# 不偏推定量 θ~
theta_tilde = np.exp(X_bar - 1/(2*n_samples))
theta_tilde_estimates.append(theta_tilde)
# 推定量の平均を計算
theta_hat_mean = np.mean(theta_hat_estimates)
theta_tilde_mean = np.mean(theta_tilde_estimates)
# グラフ描画
plt.figure(figsize=(12, 6))
# ヒストグラムの描画
plt.hist(theta_hat_estimates, bins=100, density=True, alpha=0.6, color='blue', label='$\\hat{\\theta}$ (最尤推定量)')
plt.hist(theta_tilde_estimates, bins=100, density=True, alpha=0.6, color='green', label='$\\tilde{\\theta}$ (不偏推定量)')
# 真の値を赤線で表示
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=2, label=f'真の$\\theta$: {theta_true:.2f}')
# θハットとθチルダの平均をそれぞれ緑線と青線で表示
plt.axvline(theta_hat_mean, color='blue', linestyle='dotted', linewidth=2, label=f'$\\hat{{\\theta}}$平均: {theta_hat_mean:.2f}')
plt.axvline(theta_tilde_mean, color='green', linestyle='dotted', linewidth=2, label=f'$\\tilde{{\\theta}}$平均: {theta_tilde_mean:.2f}')
# グラフのタイトルとラベル
plt.title('$\\hat{\\theta}$ と $\\tilde{\\theta}$ の分布', fontsize=16)
plt.xlabel('$\\theta$', fontsize=14)
plt.ylabel('密度', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
plt.show()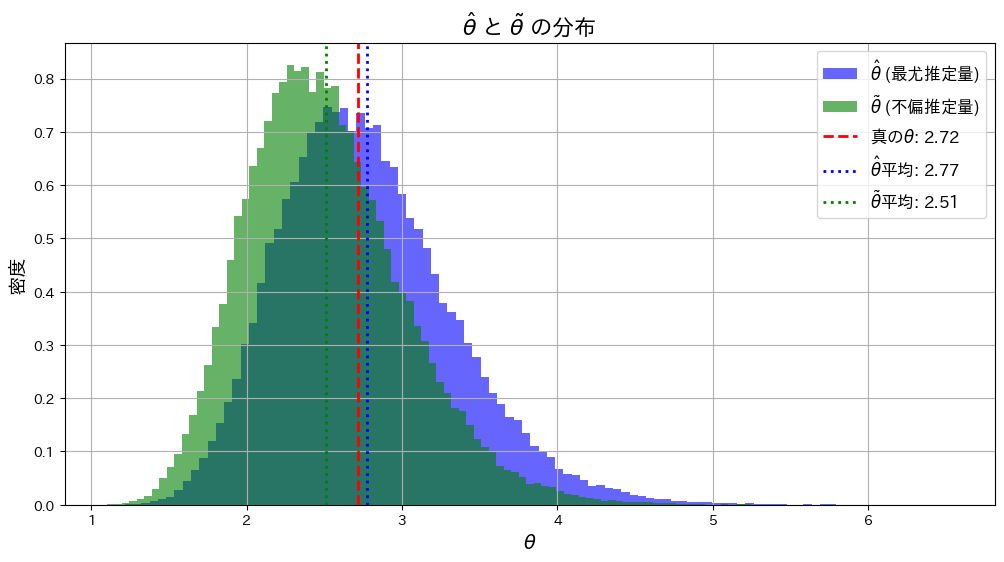
![]() は
は![]() よりも真のθに近くなっています。これはサンプルサイズnが小さいことと、および推定量の分散の違いが起因しているのかもしれません。
よりも真のθに近くなっています。これはサンプルサイズnが小さいことと、および推定量の分散の違いが起因しているのかもしれません。
次に、サンプルサイズn=5, 10, 20, 50と変化させて、この乖離がどのように変わるかを確認します。
# 2016 Q1(2) 2024.11.12
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
mu_true = 1.0 # 真の平均 (mu)
theta_true = np.exp(mu_true) # 真の theta = e^mu
n_trials = 100000 # シミュレーション試行回数
sample_sizes = [5, 10, 20, 50] # サンプルサイズのリスト
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.ravel() # 2x2 の配列を平坦化
for i, n_samples in enumerate(sample_sizes):
theta_hat_estimates = []
theta_tilde_estimates = []
for _ in range(n_trials):
sample = np.random.normal(loc=mu_true, scale=1/np.sqrt(n_samples), size=n_samples)
X_bar = np.mean(sample)
# 最尤推定量
theta_hat = np.exp(X_bar)
theta_hat_estimates.append(theta_hat)
# 不偏推定量
theta_tilde = np.exp(X_bar - 1/(2*n_samples))
theta_tilde_estimates.append(theta_tilde)
theta_hat_mean = np.mean(theta_hat_estimates)
theta_tilde_mean = np.mean(theta_tilde_estimates)
# ヒストグラムのプロット
axes[i].hist(theta_hat_estimates, bins=100, density=True, alpha=0.6, color='blue', label='$\\hat{\\theta}$ (最尤推定量)')
axes[i].hist(theta_tilde_estimates, bins=100, density=True, alpha=0.6, color='green', label='$\\tilde{\\theta}$ (不偏推定量)')
axes[i].axvline(theta_true, color='red', linestyle='dashed', linewidth=2, label=f'真の$\\theta$: {theta_true:.2f}')
axes[i].axvline(theta_hat_mean, color='blue', linestyle='dotted', linewidth=2, label=f'$\\hat{{\\theta}}$平均: {theta_hat_mean:.2f}')
axes[i].axvline(theta_tilde_mean, color='green', linestyle='dotted', linewidth=2, label=f'$\\tilde{{\\theta}}$平均: {theta_tilde_mean:.2f}')
axes[i].set_title(f'サンプルサイズ n={n_samples}')
axes[i].set_xlabel('$\\theta$')
axes[i].set_ylabel('密度')
axes[i].legend()
axes[i].grid(True)
plt.suptitle('$\\hat{\\theta}$ と $\\tilde{\\theta}$ の分布', fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()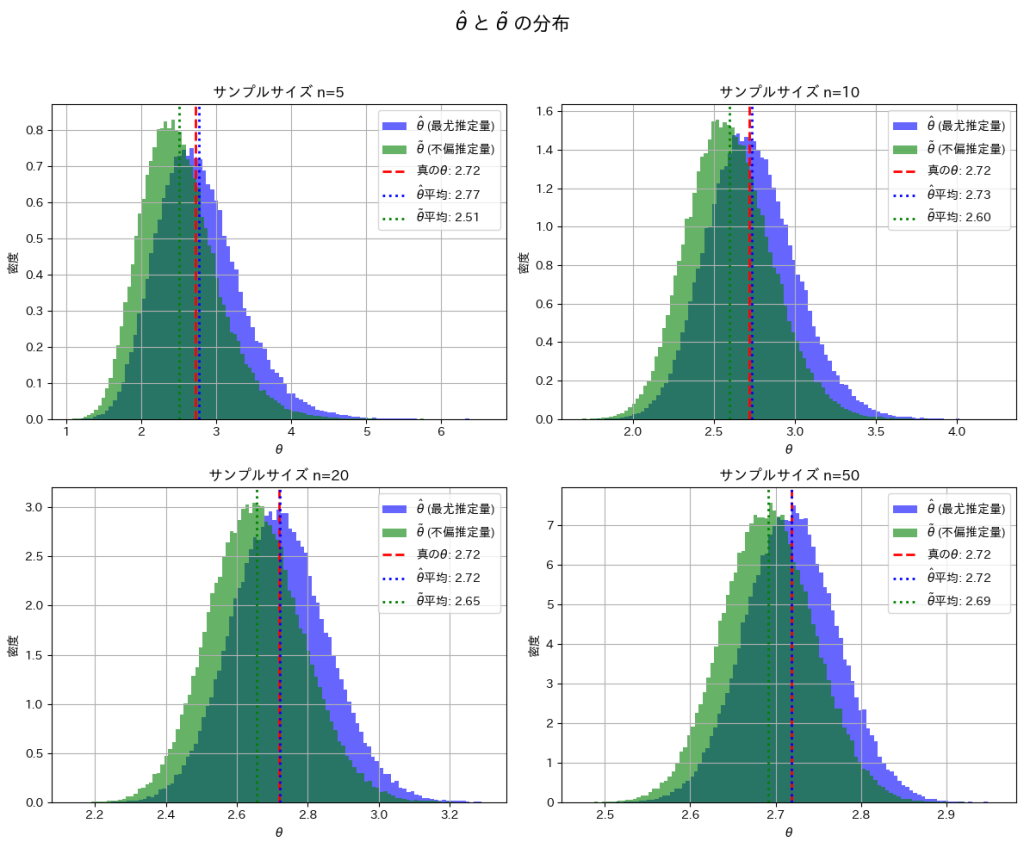
nを大きくすることで、![]() と
と![]() は真のθの間の乖離が小さくなることを確認できました。
は真のθの間の乖離が小さくなることを確認できました。
次に、nを変化させて![]() と
と![]() がどのように変化するか折れ線グラフで見てみます。
がどのように変化するか折れ線グラフで見てみます。
# 2016 Q1(2) 2024.11.12
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
mu_true = 1.0 # 真の平均 (mu)
theta_true = np.exp(mu_true) # 真の theta = e^mu
n_trials = 100000 # シミュレーション試行回数
sample_sizes = np.arange(5, 101, 5) # サンプルサイズ n の範囲 [5, 10, ..., 100]
# 推定量の平均値を格納するリスト
theta_hat_means = []
theta_tilde_means = []
# サンプルサイズを変化させてシミュレーション
for n_samples in sample_sizes:
theta_hat_estimates = []
theta_tilde_estimates = []
for _ in range(n_trials):
sample = np.random.normal(loc=mu_true, scale=1/np.sqrt(n_samples), size=n_samples)
X_bar = np.mean(sample)
# 最尤推定量
theta_hat = np.exp(X_bar)
theta_hat_estimates.append(theta_hat)
# 不偏推定量
theta_tilde = np.exp(X_bar - 1/(2*n_samples))
theta_tilde_estimates.append(theta_tilde)
# 平均値を格納
theta_hat_means.append(np.mean(theta_hat_estimates))
theta_tilde_means.append(np.mean(theta_tilde_estimates))
# 折れ線グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, theta_hat_means, marker='o', linestyle='-', color='blue', label='$\\hat{\\theta}$ (最尤推定量)')
plt.plot(sample_sizes, theta_tilde_means, marker='s', linestyle='-', color='green', label='$\\tilde{\\theta}$ (不偏推定量)')
plt.axhline(y=theta_true, color='red', linestyle='dashed', linewidth=2, label=f'真の$\\theta$: {theta_true:.2f}')
# ラベルとタイトル
plt.title('サンプルサイズ n に対する $\\hat{\\theta}$ と $\\tilde{\\theta}$ の平均値', fontsize=16)
plt.xlabel('サンプルサイズ $n$', fontsize=14)
plt.ylabel('$\\theta$の平均値', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
plt.show()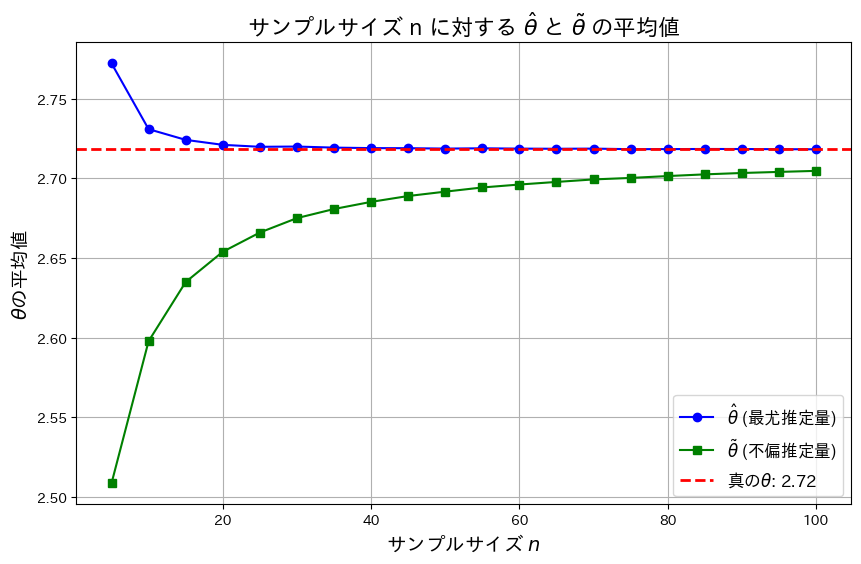
![]() は真のθよりも大きい値を取り、徐々に減少し真のθに近づきます。一方
は真のθよりも大きい値を取り、徐々に減少し真のθに近づきます。一方![]() 真のθよりも小さい値を取り、徐々に増加し真のθに近づきます。また近づくスピードは
真のθよりも小さい値を取り、徐々に増加し真のθに近づきます。また近づくスピードは![]() のほうが早く、
のほうが早く、![]() の分散が
の分散が![]() の分散よりも小さいことが分かります。
の分散よりも小さいことが分かります。
2016 Q1(1)
正規分布の母平均μに対してθ=exp(μ)をパラメータとする最尤推定を行いました。
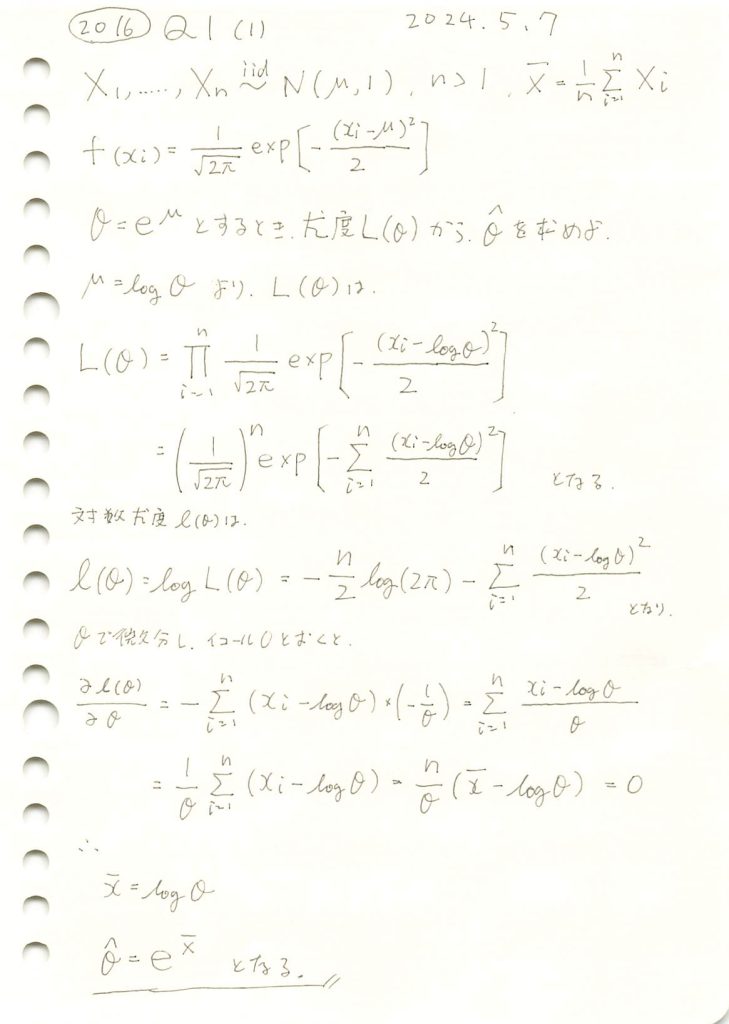
コード
![]() が真のθに近づくか確認するためシミュレーションを行います。まずはサンプルサイズn=5でやってみます。
が真のθに近づくか確認するためシミュレーションを行います。まずはサンプルサイズn=5でやってみます。
# 2016 Q1(1) 2024.11.11
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
mu_true = 1.0 # 真の平均 (mu)
theta_true = np.exp(mu_true) # 真の theta = e^mu
n_samples = 5 # サンプル数
n_trials = 100000 # シミュレーション試行回数
# 乱数生成と最尤推定量の計算
theta_estimates = []
for _ in range(n_trials):
sample = np.random.normal(loc=mu_true, scale=1, size=n_samples) # 正規分布からサンプルを生成
mu_hat = np.mean(sample) # 平均値を計算 (muの最尤推定量)
theta_hat = np.exp(mu_hat) # theta = e^mu の推定値
theta_estimates.append(theta_hat)
# 真の値とシミュレーションの平均を計算
theta_hat_mean = np.mean(theta_estimates)
# 真の値と推定量の平均値を表示
print(f"真の θ: {theta_true:.4f}")
print(f"θハットの平均値 (シミュレーション): {theta_hat_mean:.4f}")
# グラフの描画
plt.hist(theta_estimates, bins=100, density=True, alpha=0.6, color='blue', label='シミュレーションによる$\hat{\\theta}$')
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=2, label=f'真の$\\theta$: {theta_true:.2f}')
plt.axvline(theta_hat_mean, color='green', linestyle='dashed', linewidth=2, label=f'$\\hat{{\\theta}}$平均: {theta_hat_mean:.2f}')
plt.title('$\\hat{\\theta}$の分布(最尤推定量)')
plt.xlabel('$\\theta$')
plt.ylabel('密度')
plt.legend()
plt.grid(True)
plt.show()
真の θ: 2.7183
θハットの平均値 (シミュレーション): 3.0120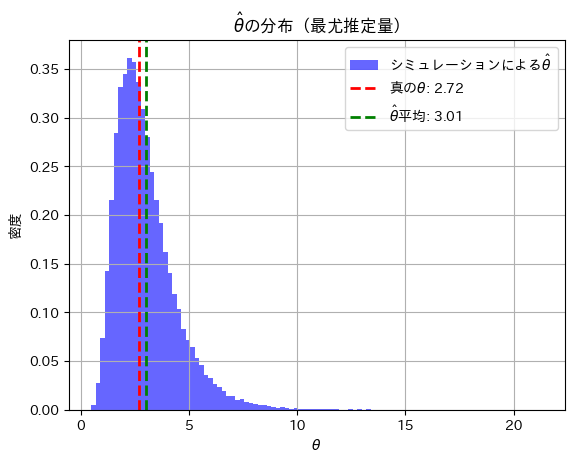
![]() と真のθの間に少し乖離が見られます。サンプルサイズnが小さいことが起因しているかもしれません。
と真のθの間に少し乖離が見られます。サンプルサイズnが小さいことが起因しているかもしれません。
次に、サンプルサイズn=5, 10, 20, 50と変化させて、この乖離がどのように変わるかを確認してみます。
# 2016 Q1(1) 2024.11.11
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
mu_true = 1.0 # 真の平均 (mu)
theta_true = np.exp(mu_true) # 真の theta = e^mu
n_trials = 100000 # シミュレーション試行回数
sample_sizes = [5, 10, 20, 50] # サンプルサイズのリスト
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.ravel() # 2x2 の配列を平坦化
for i, n_samples in enumerate(sample_sizes):
theta_estimates = []
for _ in range(n_trials):
sample = np.random.normal(loc=mu_true, scale=1, size=n_samples)
mu_hat = np.mean(sample)
theta_hat = np.exp(mu_hat)
theta_estimates.append(theta_hat)
theta_hat_mean = np.mean(theta_estimates)
# ヒストグラムのプロット
axes[i].hist(theta_estimates, bins=100, density=True, alpha=0.6, color='blue', label='シミュレーションによる$\hat{\\theta}$')
axes[i].axvline(theta_true, color='red', linestyle='dashed', linewidth=2, label=f'真の$\\theta$: {theta_true:.2f}')
axes[i].axvline(theta_hat_mean, color='green', linestyle='dashed', linewidth=2, label=f'$\\hat{{\\theta}}$平均: {theta_hat_mean:.2f}')
axes[i].set_title(f'サンプルサイズ n={n_samples}')
axes[i].set_xlabel('$\\theta$')
axes[i].set_ylabel('密度')
axes[i].legend()
axes[i].grid(True)
plt.suptitle('$\\hat{\\theta}$の分布(最尤推定量)', fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()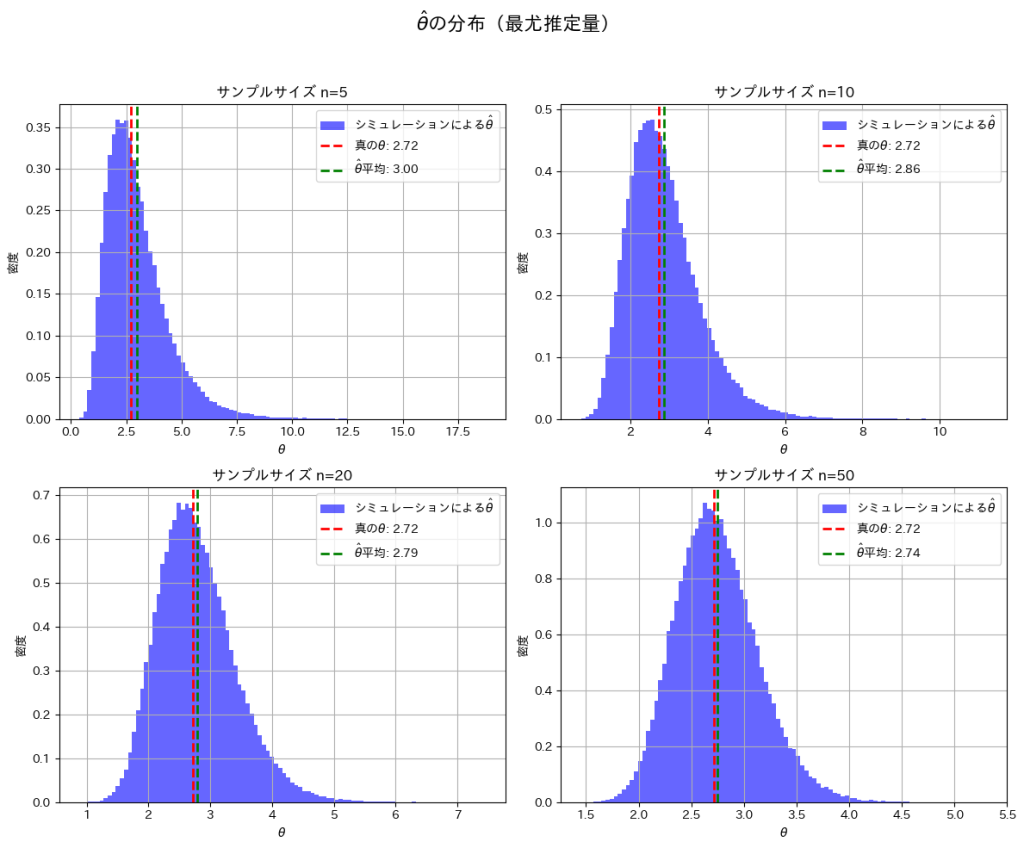
nを大きくすることで、![]() と真のθの間の乖離が小さくなることを確認できました。
と真のθの間の乖離が小さくなることを確認できました。
2017 Q2(1)
一様分布の上限の最尤推定量を求めました。

コード
θ=10,n=20としてシミュレーションを行い、![]() の分布を見てみます。
の分布を見てみます。
# 2017 Q2(1) 2024.10.29
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
theta_true = 10 # 真の θ の値
n = 20 # 1試行あたりのサンプル数
num_trials = 1000 # シミュレーションの試行回数
# シミュレーションを実行
theta_estimates = []
for _ in range(num_trials):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプルの最大値を推定値 θ_hat として記録
theta_hat = np.max(samples)
theta_estimates.append(theta_hat)
# 推定値の分布をヒストグラムで表示
plt.hist(theta_estimates, bins=30, edgecolor='black', density=True)
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'$\hat{\theta}$')
plt.ylabel('密度')
plt.title(r'$\hat{\theta} = X_{\max}$ の分布')
plt.legend()
plt.show()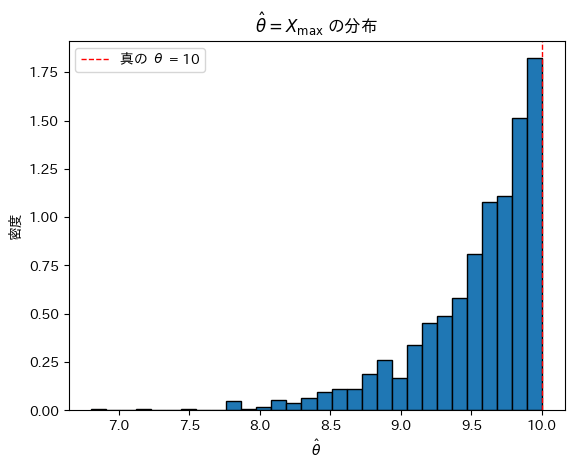
![]() は真のθより大きくならないため、結果としてθよりやや小さな値を取っているように見えます。
は真のθより大きくならないため、結果としてθよりやや小さな値を取っているように見えます。
次にサンプルサイズnを変化させて最尤推定量![]() がどうなるのか確認をします。
がどうなるのか確認をします。
# 2017 Q2(1) 2024.10.29
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
max_n = 100 # 最大サンプルサイズ
num_trials_per_n = 100 # 各サンプルサイズでの試行回数
# 各サンプルサイズにおける θ^ の平均を記録
theta_hat_means = []
# サンプルサイズ n を 1 から max_n まで増やしながらシミュレーション
for n in range(1, max_n + 1):
theta_estimates = []
for _ in range(num_trials_per_n):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプルの最大値を推定値 θ_hat として記録
theta_hat = np.max(samples)
theta_estimates.append(theta_hat)
# 各 n に対する θ^ の平均を保存
theta_hat_means.append(np.mean(theta_estimates))
# グラフ描画
plt.plot(range(1, max_n + 1), theta_hat_means, label=r'$\mathbb{E}[\hat{\theta}]$')
plt.axhline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'サンプルサイズ $n$')
plt.ylabel(r'推定量 $\hat{\theta}$ の平均')
plt.title(r'サンプルサイズ $n$ と $\hat{\theta}$ の関係')
plt.legend()
plt.show()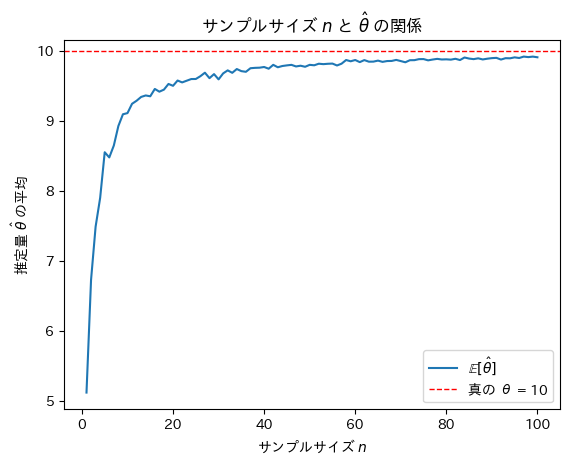
サンプルサイズnが増加するにつれて最尤推定量![]() は真のθに近づくことが確認できました。
は真のθに近づくことが確認できました。
2017 Q1(5)
正規分布の分散の最尤推定量を母平均が既知の場合と未知の場合でそれぞれ求めましまた。

コード
サンプルサイズnを50に固定し尤度関数を可視化します。また最尤推定量 ![]() と
と![]() をプロットしてみます。
をプロットしてみます。
# 2017 Q1(5) 2024.10.28
# 最尤推定量 (T^2, S^2) の計算と尤度関数の可視化
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# シミュレーションパラメータの設定
mu = 5.0 # 母平均(既知)
sigma = 2.0 # 母標準偏差(√母分散)
selected_sample_size = 50 # 固定サンプルサイズ
true_variance = sigma**2 # 母分散
# 正規分布からのサンプル生成(サンプルサイズは selected_sample_size で固定)
sample = np.random.normal(mu, sigma, selected_sample_size) # 固定サンプル生成
# 最尤推定量の計算
T2 = np.sum((sample - mu) ** 2) / selected_sample_size # 最尤推定量 T^2 の計算 (μが既知)
sample_mean = np.mean(sample)
S2 = np.sum((sample - sample_mean) ** 2) / (selected_sample_size - 1) # 最尤推定量 S^2 の計算 (μが未知)
# 尤度関数のプロットのためのパラメータ設定
sigma_squared_trial_values = np.linspace(0.1, 5.0, 100) # σ^2 の値を試行的に設定
likelihoods = [] # 尤度関数の値を保存するリスト
# 尤度関数の計算(固定サンプルに基づく)
for sigma_squared_trial in sigma_squared_trial_values:
likelihood = np.prod(norm.pdf(sample, loc=mu, scale=np.sqrt(sigma_squared_trial))) # 尤度関数の値を計算
likelihoods.append(likelihood)
# グラフの作成
plt.figure(figsize=(10, 6))
plt.plot(sigma_squared_trial_values, likelihoods, label='尤度関数', color='blue')
plt.axvline(x=T2, color='green', linestyle='--', label='$T^2$ (最尤推定量, μが既知)', linewidth=2)
plt.axvline(x=S2, color='orange', linestyle='--', label='$S^2$ (最尤推定量, μが未知)', linewidth=2)
plt.axvline(x=true_variance, color='red', linestyle='-.', label='母分散 $\\sigma^2$', linewidth=2)
plt.title(f'サンプルサイズ {selected_sample_size} における尤度関数と推定量の比較')
plt.xlabel('$\sigma^2$ の試行値')
plt.ylabel('尤度')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()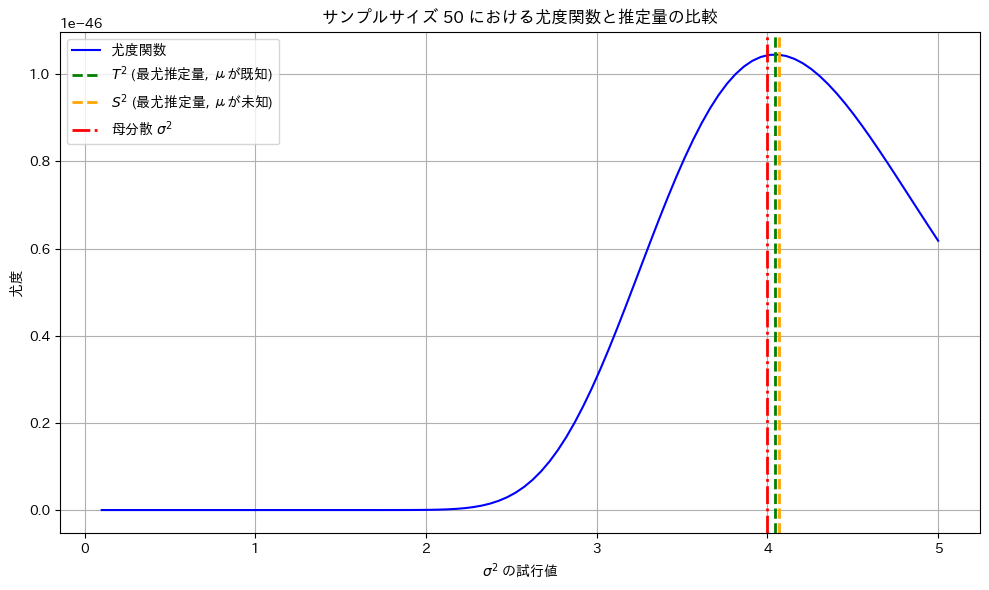
最尤推定量 ![]() と
と![]() は尤度が最大となる
は尤度が最大となる![]() の値を取っています。
の値を取っています。
もう一度実行してみます。
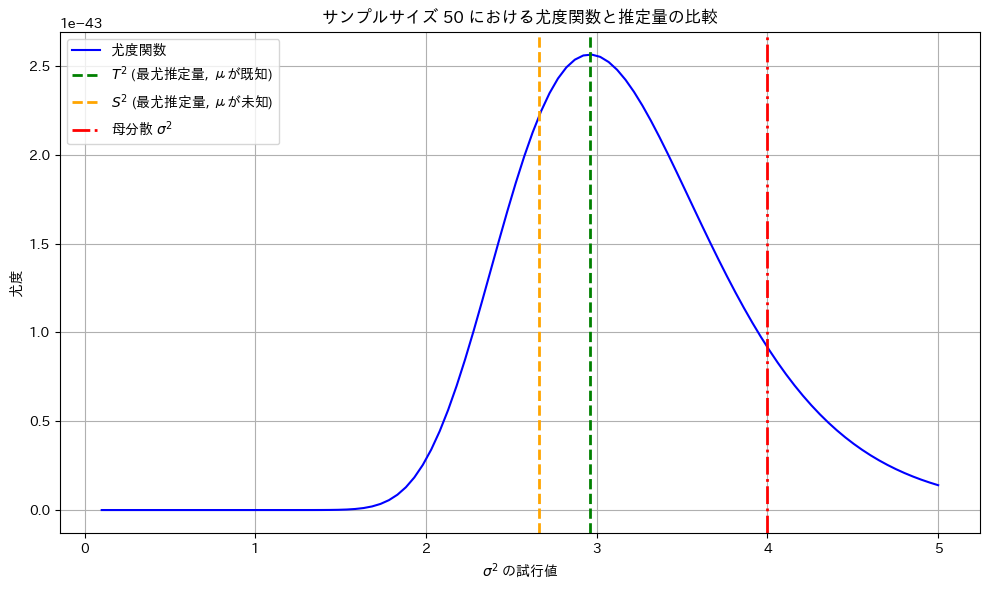
サンプルによっては最尤推定量![]() と
と![]() は
は![]() から乖離する場合もあります。
から乖離する場合もあります。
次に、サンプルサイズを大きくすることで母分散に近づくことを確認します。
# 2017 Q1(5) 2024.10.28
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータの設定
mu = 5.0 # 母平均(既知)
sigma = 2.0 # 母標準偏差(√母分散)
true_variance = sigma**2 # 母分散
sample_sizes = range(50, 10050, 50) # サンプルサイズを設定
# シミュレーション結果を保存するリスト
T2_estimates = [] # μが既知の場合の推定量 T^2
S2_estimates = [] # μが未知の場合の推定量 S^2
# 各サンプルサイズでのシミュレーションの実行
for n in sample_sizes:
# 正規分布からサンプルを抽出
sample = np.random.normal(mu, sigma, n)
# μが既知の場合の最尤推定量 T^2
T2 = np.sum((sample - mu) ** 2) / n
# μが未知の場合の最尤推定量 S^2
sample_mean = np.mean(sample)
S2 = np.sum((sample - sample_mean) ** 2) / (n - 1)
# 推定量をリストに保存
T2_estimates.append(T2)
S2_estimates.append(S2)
# グラフの作成(理論値を追加)
plt.figure(figsize=(12, 8))
# μが既知の場合のプロット (緑)
plt.plot(sample_sizes, T2_estimates, marker='o', color='green', label='$T^2$ (μが既知の場合)', linestyle='--')
# μが未知の場合のプロット (オレンジ)
plt.plot(sample_sizes, S2_estimates, marker='x', color='orange', label='$S^2$ (μが未知の場合)', linestyle='--')
# 理論値の線を追加 (赤)
plt.axhline(y=true_variance, color='red', linestyle='-.', label='理論値: $\sigma^2$', linewidth=2)
# グラフの設定
plt.title('最尤推定量 $T^2$ と $S^2$ のサンプルサイズごとの結果')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('推定量')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()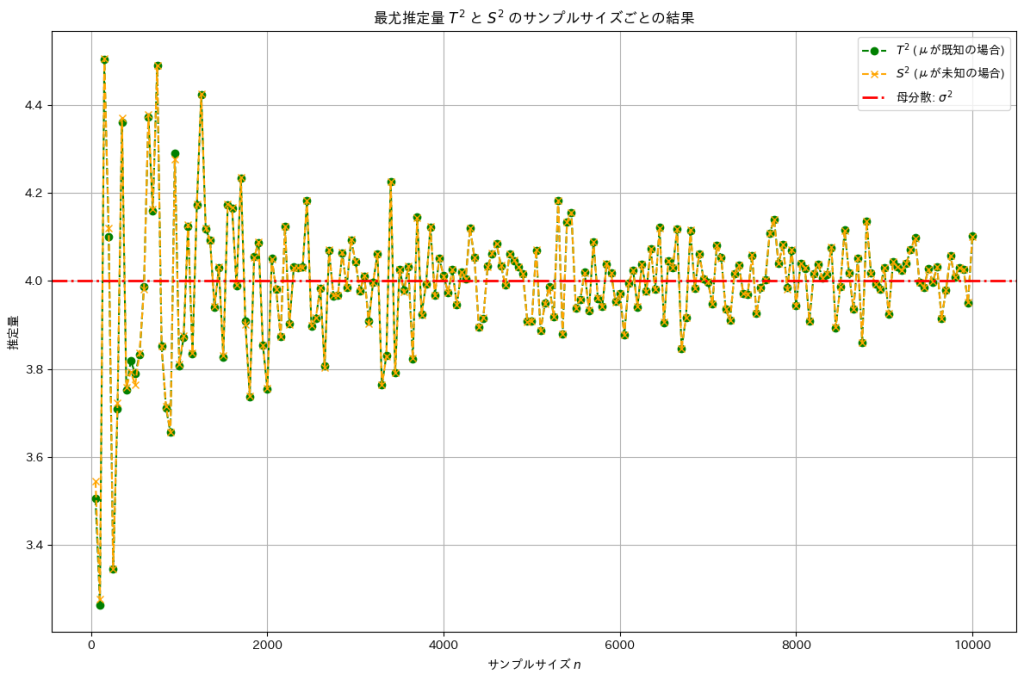
サンプルサイズを大きくすることで最尤推定量![]() と
と![]() は母分散
は母分散![]() に近づきました。
に近づきました。
2021 Q3(4)
ポアソン分布のパラメータλの区間推定の中点がその最尤推定値より大きくなることを学びました。面白い。

コード
ポアソン分布の確率質量関数にλに3,5,10を与えてプロットします
#2021 Q3(4) 2024.8.30
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# パラメータ設定
lambda_values = [3, 5, 10] # 異なる λ の値
max_x = 25 # x軸の最大値(PMFの表示範囲)
# プロットの設定
plt.figure(figsize=(12, 6))
# 各 λ について PMF を計算し、プロット
for lambda_value in lambda_values:
x = np.arange(0, max_x + 1) # x軸の範囲
pmf = poisson.pmf(x, lambda_value) # PMF を計算
plt.plot(x, pmf, marker='o', label=f'λ = {lambda_value}')
# グラフの装飾
plt.title('ポアソン分布の確率質量関数(PMF)の比較')
plt.xlabel('x')
plt.ylabel('P(X=x)')
plt.legend()
plt.grid(True)
plt.show()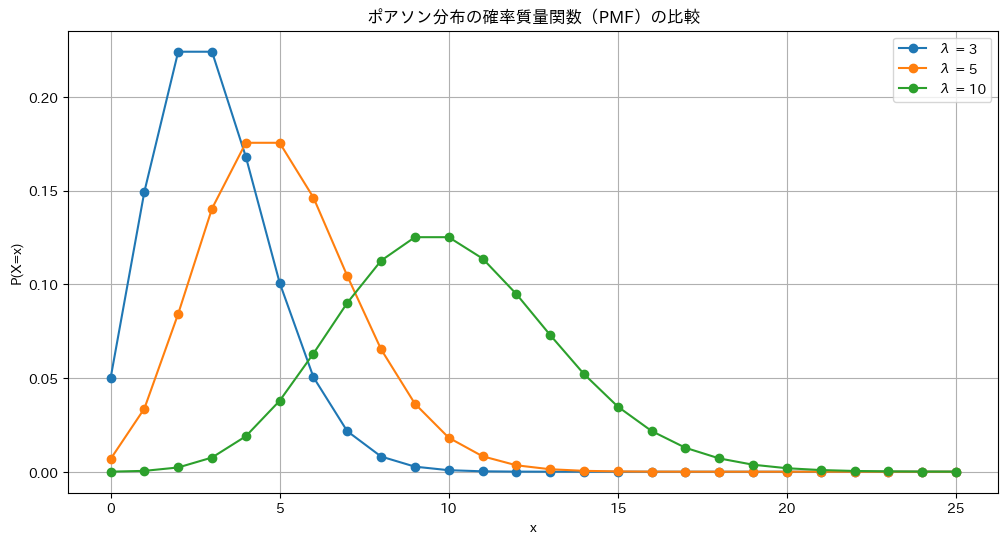
λが大きくなるほど分散も大きくなります
λの信頼区間と最尤推定値の関係を見てみます
#2021 Q3(4) 2024.8.30
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
lambda_true = 5 # 真の λ の値
n = 10 # サンプル数
num_simulations = 1000 # シミュレーション回数
# 信頼区間と最尤推定値の保存リスト
lambda_L_values = []
lambda_U_values = []
lambda_hat_values = []
# シミュレーション開始
for _ in range(num_simulations):
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_true, n)
T = np.sum(samples) # T を計算
# 最尤推定値を計算
lambda_hat = T / n
# 信頼区間の計算
lambda_L = (T - 2*np.sqrt(T + 1) + 2) / n
lambda_U = (T + 2*np.sqrt(T + 1) + 2) / n
# 結果を保存
lambda_L_values.append(lambda_L)
lambda_U_values.append(lambda_U)
lambda_hat_values.append(lambda_hat)
# 信頼区間の中点の計算
lambda_M_values = [(lambda_L_values[i] + lambda_U_values[i]) / 2 for i in range(num_simulations)]
lambda_M_mean = np.mean(lambda_M_values)
# 最尤推定値の平均を計算
lambda_hat_mean = np.mean(lambda_hat_values)
# 信頼区間のプロット
plt.figure(figsize=(12, 6))
for i in range(num_simulations):
plt.plot([lambda_L_values[i], lambda_U_values[i]], [i, i], color='blue')
plt.axvline(lambda_hat_mean, color='purple', linestyle='--', label='最尤推定値の平均')
plt.axvline(lambda_M_mean, color='orange', linestyle='-', label='信頼区間の中点の平均')
plt.title('信頼区間と最尤推定値の関係')
plt.xlabel('λ の値')
plt.ylabel('シミュレーション回数')
plt.legend()
plt.grid(True)
plt.show()
# 中点の平均値を表示
print(f'信頼区間の中点の平均: {lambda_M_mean:.4f}')
print(f'最尤推定値の平均: {lambda_hat_mean:.4f}')
print(f'真の λ: {lambda_true}')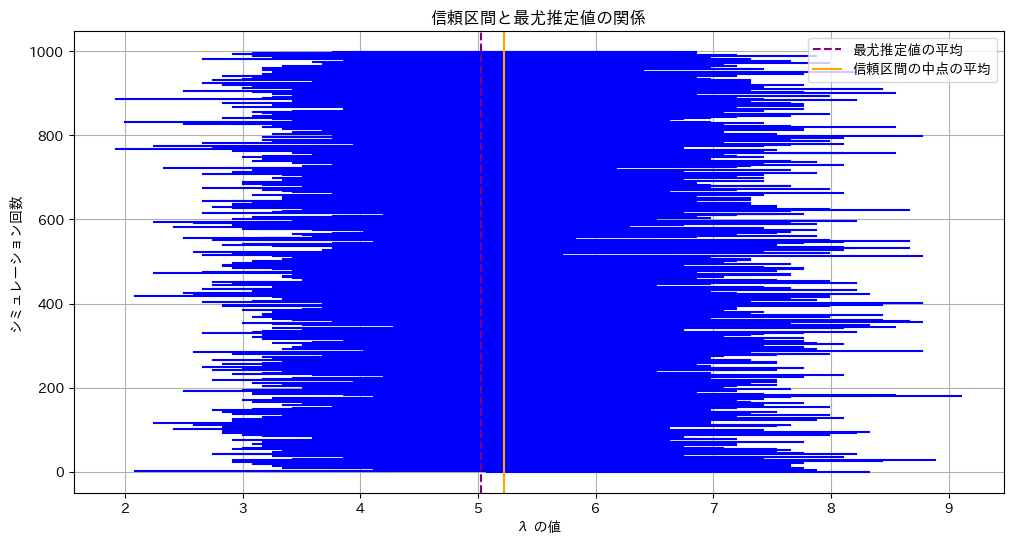
信頼区間の中点の平均: 5.2235
最尤推定値の平均: 5.0235
真の λ: 5λの信頼区間の中点は最尤推定値よりも右にずれます。λが大きくなると分散が大きくなるためです。
X=5に固定したポアソン分布の確率質量関数P(X=5|λ)のグラフを見てみます
#2021 Q3(4) 2024.8.30
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# パラメータ設定
x_value = 5 # 固定された x の値
n = 10 # サンプル数(ここでは仮に10個の観測データがあると仮定)
T = x_value * n # 合計値 T は x * n として計算
# λの範囲を指定
lambda_range = np.linspace(1, 20, 200)
# λに対するPMFを計算
pmf_values = poisson.pmf(x_value, lambda_range)
# 最尤推定値(λ_hat)を計算
lambda_hat = T / n
# 信頼区間の計算
lambda_L = (T - 2*np.sqrt(T + 1) + 2) / n
lambda_U = (T + 2*np.sqrt(T + 1) + 2) / n
lambda_M = (lambda_L + lambda_U) / 2 # 信頼区間の中点
# グラフの描画
plt.figure(figsize=(12, 6))
plt.plot(lambda_range, pmf_values, label=f'P(X={x_value})')
# 最尤推定値、信頼区間の上下限、中点を表示
plt.axvline(lambda_hat, color='red', linestyle='--', label=f'最尤推定値 λ_hat = {lambda_hat:.2f}')
plt.axvline(lambda_L, color='blue', linestyle='--', label=f'信頼区間下限 λ_L = {lambda_L:.2f}')
plt.axvline(lambda_U, color='green', linestyle='--', label=f'信頼区間上限 λ_U = {lambda_U:.2f}')
plt.axvline(lambda_M, color='orange', linestyle='-', label=f'信頼区間中点 λ_M = {lambda_M:.2f}')
# グラフの装飾
plt.title(f'ポアソン分布のPMFと信頼区間の中点(x={x_value}固定)')
plt.xlabel('λ')
plt.ylabel(f'P(X={x_value})')
plt.grid(True)
plt.legend()
plt.show()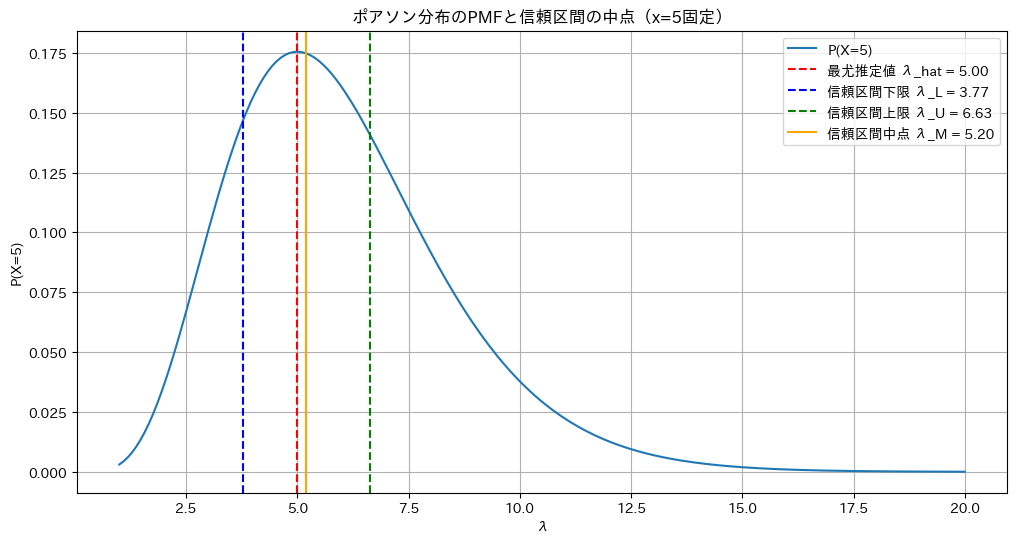
右に裾が長く、λの信頼区間の中点は最尤推定値よりも右にズレていることが分かります。
なお、このグラフは、ボソン分布の確率質量関数
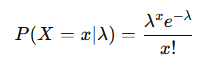
より
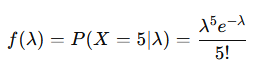
となります。これは、k=6 , θ=1 としたときガンマ分布に一致します
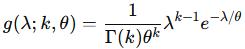
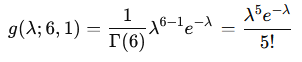
2021 Q3(2)[2-3]
ポアソン分布に従う確率変数の和Tからλの最尤推定量を求める問題をやりました。
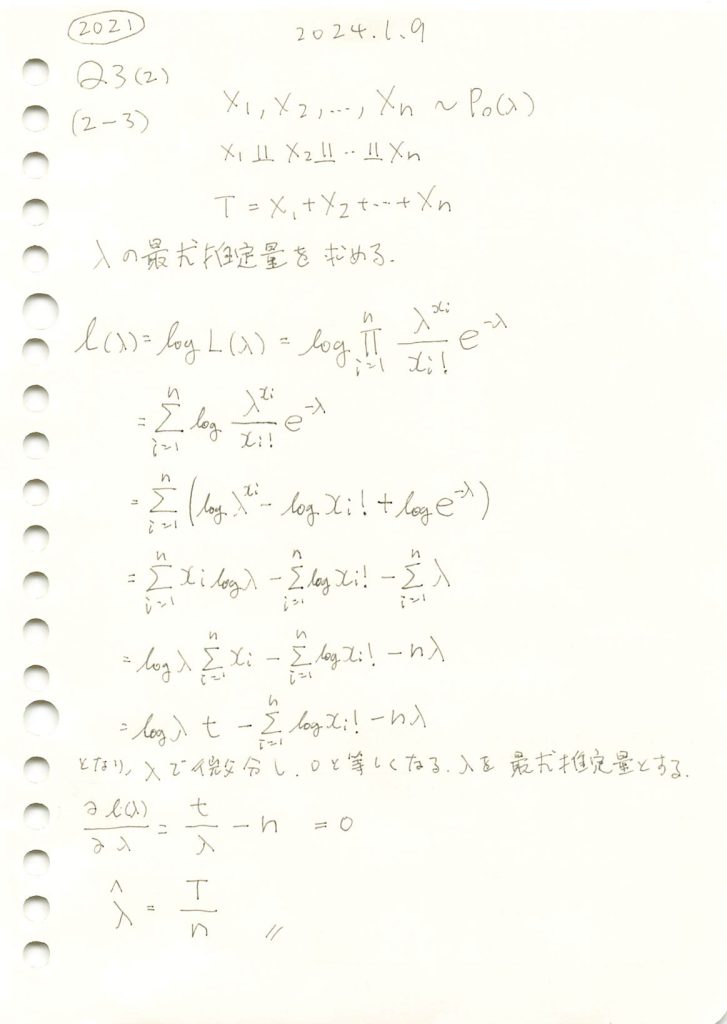
あとがき
![]() の式で計算すると簡単。
の式で計算すると簡単。
コード
scipyのminimizeで、最尤推定量を探索する。
# 2021 Q3(2)[2-3] 2024.8.28
import numpy as np
from scipy.optimize import minimize
from scipy.stats import poisson
# パラメータの設定
lambda_value = 5 # 真のパラメータ(実際のλ)
n = 10 # サンプル数
num_simulations = 1000 # シミュレーション回数
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_value, n)
# 尤度関数(負の対数尤度関数)
def negative_log_likelihood(lambda_hat, data):
# ポアソン分布に基づく対数尤度を計算。minimizeを用いるためマイナス符号をつける
return -np.sum(poisson.logpmf(data, lambda_hat))
# 最尤推定量の推定
initial_guess = np.mean(samples) # 初期値としてサンプルの平均を使用
result = minimize(negative_log_likelihood, x0=initial_guess, args=(samples,), bounds=[(0.001, None)])
lambda_mle = result.x[0]
# 結果を表示
print(f"実際のλ: {lambda_value}")
print(f"推定されたλの最尤推定値: {lambda_mle}")実際のλ: 5
推定されたλの最尤推定値: 4.9尤度関数のグラフを確認
# 2021 Q3(2)[2-3] 2024.8.28
import numpy as np
from scipy.stats import poisson
import matplotlib.pyplot as plt
# パラメータの設定
lambda_value = 5 # 真のパラメータ(実際のλ)
n = 10 # サンプル数
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_value, n)
# 尤度関数を定義
def likelihood(lambda_hat, data):
return np.prod(poisson.pmf(data, lambda_hat))
# 尤度関数と対数尤度関数の計算
lambda_range = np.linspace(0.1, 10, 500) # すべてのグラフで共通の範囲
likelihood_values = [likelihood(l, samples) for l in lambda_range]
log_likelihood_values = np.log(likelihood_values)
# 最大の尤度を与えるλを求める
max_likelihood_lambda = lambda_range[np.argmax(likelihood_values)]
# グラフのプロット
fig, ax = plt.subplots(2, 1, figsize=(10, 6))
# 尤度関数のプロット
ax[0].plot(lambda_range, likelihood_values, label='尤度', color='blue')
ax[0].axvline(x=max_likelihood_lambda, color='red', linestyle='--', label=f'最大尤度 λ = {max_likelihood_lambda:.2f}')
ax[0].set_title("尤度関数")
ax[0].set_xlabel("λ の値")
ax[0].set_ylabel("尤度")
ax[0].set_xlim(lambda_range[0], lambda_range[-1]) # 横軸を合わせる
ax[0].legend()
ax[0].grid(True)
# 対数尤度関数のプロット
ax[1].plot(lambda_range, log_likelihood_values, label='対数尤度', color='green')
ax[1].axvline(x=max_likelihood_lambda, color='red', linestyle='--', label=f'最大尤度 λ = {max_likelihood_lambda:.2f}')
ax[1].set_title("対数尤度関数")
ax[1].set_xlabel("λ の値")
ax[1].set_ylabel("対数尤度")
ax[1].set_xlim(lambda_range[0], lambda_range[-1]) # 横軸を合わせる
ax[1].legend()
ax[1].grid(True)
# グラフの表示
plt.tight_layout()
plt.show()
# 最終結果の表示
print(f"実際のλ: {lambda_value}")
print(f"推定されたλの最尤推定値: {max_likelihood_lambda}")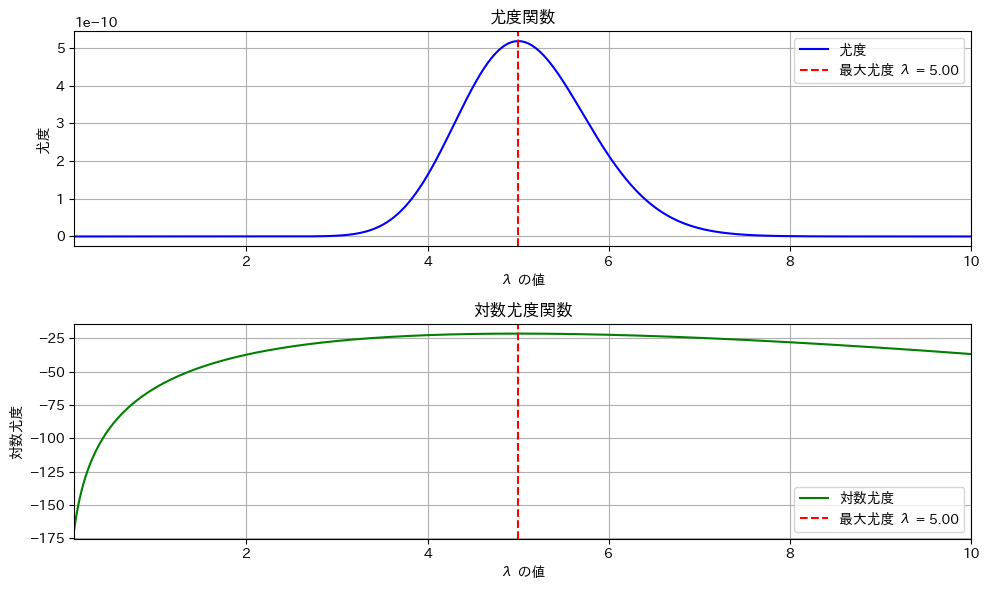
尤度関数でも対数尤度関数でも同じλでピークになる。
nが小さいとλの推定量の分散が大きくなるので誤差が大きくなる。上のグラフはたまたま5.00になった。n=100ぐらいにすると安定する。
シミュレーションによる計算
# 2021 Q3(2)[2-3] 2024.8.28
import numpy as np
# パラメータの設定
lambda_value = 5 # 真のパラメータ(実際のλ)
n = 10 # サンプル数
num_simulations = 1000 # シミュレーション回数
# ポアソン分布に従う n 個のサンプルを num_simulations 回生成
samples = np.random.poisson(lambda_value, (num_simulations, n))
# 各サンプルの和 T を計算
T = np.sum(samples, axis=1)
# λ の最尤推定量を計算
lambda_hat = T / n
# 結果を表示
print(f"実際のλ: {lambda_value}")
print(f"推定されたλの平均: {np.mean(lambda_hat)}")
print(f"推定されたλの分散: {np.var(lambda_hat)}")実際のλ: 5
推定されたλの平均: 5.0058
推定されたλの分散: 0.49292636