ホーム » マルコフ性
「マルコフ性」カテゴリーアーカイブ
2018 Q4(3)
マルコフ連鎖する条件付き正規分布の任意のtに対する分布の証明をやりました。

コード
![]() の条件付き分布が
の条件付き分布が![]() に従うのかシミュレーションをしてみます。
に従うのかシミュレーションをしてみます。
# 2018 Q4(3) 2024.10.20
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
t_max = 50 # 時間 t の最大値
n_simulations = 10000 # シミュレーション回数
rho = 0.7 # ρの値
x_0 = 1.0 # X_0 の初期値
# シミュレーション結果を格納するリスト
X_t_samples = np.zeros((t_max, n_simulations))
X_t_samples[0, :] = x_0 # X_0 = x_0
# マルコフプロセスをシミュレーション
for t in range(1, t_max):
# X_t を次のステップで生成
mean = rho**2 * X_t_samples[t-1, :]
variance = 1 - rho**4
X_t_samples[t, :] = np.random.normal(loc=mean, scale=np.sqrt(variance), size=n_simulations)
# シミュレーション結果の平均と分散を計算
simulated_means = np.mean(X_t_samples, axis=1)
simulated_variances = np.var(X_t_samples, axis=1)
# 理論値の期待値と分散を計算
theoretical_means = rho**(2 * np.arange(t_max)) * x_0
theoretical_variances = 1 - rho**(4 * np.arange(t_max))
# グラフを描画
plt.figure(figsize=(10, 6))
# 期待値のプロット
plt.subplot(2, 1, 1)
plt.plot(np.arange(t_max), simulated_means, label="シミュレーション期待値", color='blue', linestyle='--')
plt.plot(np.arange(t_max), theoretical_means, label="理論期待値", color='red')
plt.title("期待値の推移")
plt.xlabel("時間 t")
plt.ylabel("期待値 E[X_t]")
plt.legend()
plt.grid(True)
# 分散のプロット
plt.subplot(2, 1, 2)
plt.plot(np.arange(t_max), simulated_variances, label="シミュレーション分散", color='blue', linestyle='--')
plt.plot(np.arange(t_max), theoretical_variances, label="理論分散", color='red')
plt.title("分散の推移")
plt.xlabel("時間 t")
plt.ylabel("分散 Var[X_t]")
plt.legend()
plt.grid(True)
# グラフを表示
plt.tight_layout()
plt.show()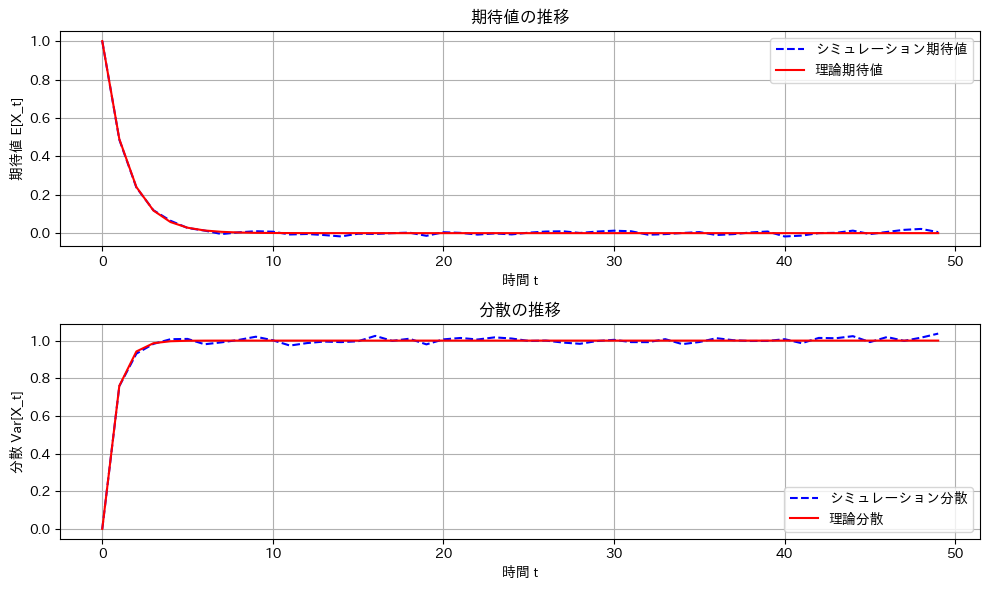
シミュレーションと理論値は一致しました。
2018 Q4(2)-2
マルコフ連鎖する条件付き正規分布の分散の問題をやりました。
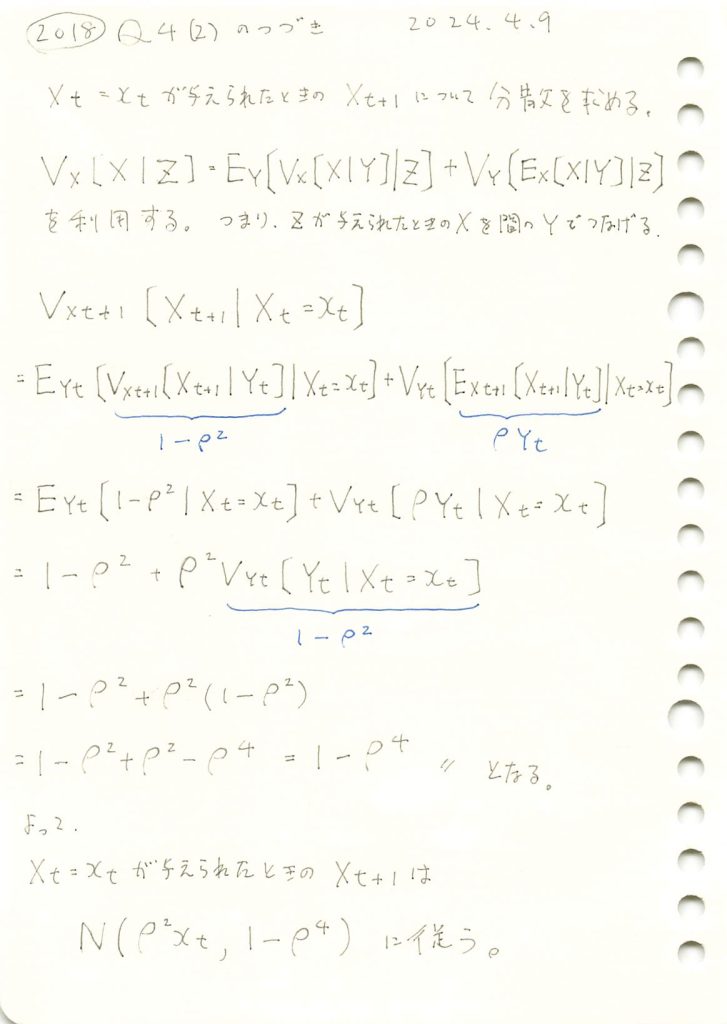
コード
![]() をシミュレーションしてみます。
をシミュレーションしてみます。
#2018 Q4(2) 2024.10.19
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n_simulations = 100000 # シミュレーション回数
rho = 0.7 # ρの値
x_t = 1.0 # X_t の初期値
# シミュレーション結果を格納するリスト
X_t1_samples = []
for _ in range(n_simulations):
# 1. X_t -> Y_t のステップ
y_t = np.random.normal(loc=rho * x_t, scale=np.sqrt(1 - rho**2))
# 2. Y_t -> X_{t+1} のステップ
x_t1 = np.random.normal(loc=rho * y_t, scale=np.sqrt(1 - rho**2))
# 結果をリストに追加
X_t1_samples.append(x_t1)
# シミュレーション結果を配列に変換
X_t1_samples = np.array(X_t1_samples)
# シミュレーション結果の期待値と分散を計算
simulated_mean = np.mean(X_t1_samples)
simulated_variance = np.var(X_t1_samples)
# 理論値の期待値と分散
expected_mean = rho**2 * x_t # 理論上の期待値
expected_variance = 1 - rho**4 # 理論上の分散
# 結果の表示
print(f"理論上の期待値: {expected_mean}, シミュレーションによる期待値: {simulated_mean}")
print(f"理論上の分散: {expected_variance}, シミュレーションによる分散: {simulated_variance}")
# ヒストグラムの表示
plt.hist(X_t1_samples, bins=50, density=True, alpha=0.6, color='g', edgecolor='black', label='シミュレーション')
plt.axvline(expected_mean, color='r', linestyle='--', label=f'理論上の期待値: {expected_mean:.3f}')
plt.title(r"$X_{t+1}$ のシミュレーション (マルコフ性)")
plt.xlabel(r"$X_{t+1}$ の値")
plt.ylabel("頻度")
plt.legend()
plt.grid(True)
plt.show()理論上の期待値: 0.48999999999999994, シミュレーションによる期待値: 0.4909842816275996
理論上の分散: 0.7599, シミュレーションによる分散: 0.7608618418358614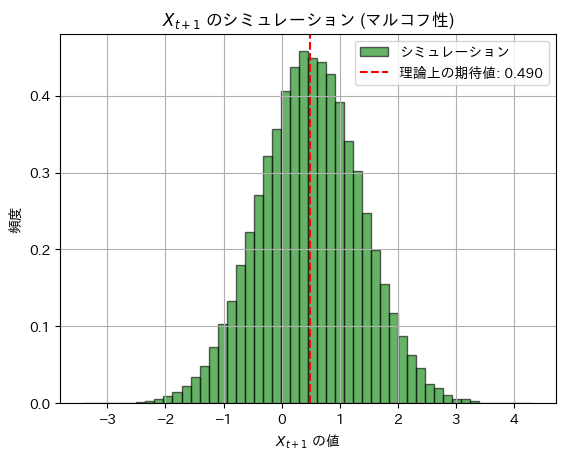
シミュレーション結果は理論値に一致しました。
2018 Q4(2)-1
マルコフ連鎖する条件付き正規分布の期待値の問題をやりました。
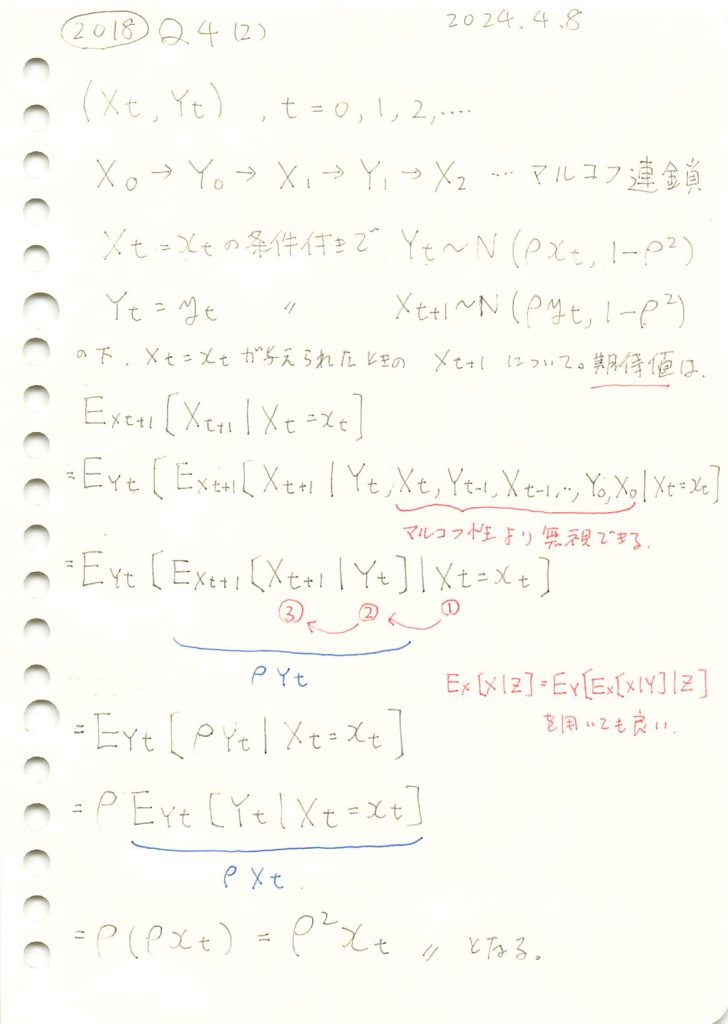
コード
![]() をシミュレーションしてみます。
をシミュレーションしてみます。
#2018 Q4(2) 2024.10.19
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n_simulations = 100000 # シミュレーション回数
rho = 0.7 # ρの値
x_t = 1.0 # X_t の初期値
# シミュレーション結果を格納するリスト
X_t1_samples = []
for _ in range(n_simulations):
# 1. X_t -> Y_t のステップ
y_t = np.random.normal(loc=rho * x_t, scale=np.sqrt(1 - rho**2))
# 2. Y_t -> X_{t+1} のステップ
x_t1 = np.random.normal(loc=rho * y_t, scale=np.sqrt(1 - rho**2))
# 結果をリストに追加
X_t1_samples.append(x_t1)
# シミュレーション結果を配列に変換
X_t1_samples = np.array(X_t1_samples)
# シミュレーション結果の期待値と分散を計算
simulated_mean = np.mean(X_t1_samples)
simulated_variance = np.var(X_t1_samples)
# 理論値の期待値と分散
expected_mean = rho**2 * x_t # 理論上の期待値
expected_variance = 1 - rho**4 # 理論上の分散
# 結果の表示
print(f"理論上の期待値: {expected_mean}, シミュレーションによる期待値: {simulated_mean}")
print(f"理論上の分散: {expected_variance}, シミュレーションによる分散: {simulated_variance}")
# ヒストグラムの表示
plt.hist(X_t1_samples, bins=50, density=True, alpha=0.6, color='g', edgecolor='black', label='シミュレーション')
plt.axvline(expected_mean, color='r', linestyle='--', label=f'理論上の期待値: {expected_mean:.3f}')
plt.title(r"$X_{t+1}$ のシミュレーション (マルコフ性)")
plt.xlabel(r"$X_{t+1}$ の値")
plt.ylabel("頻度")
plt.legend()
plt.grid(True)
plt.show()理論上の期待値: 0.48999999999999994, シミュレーションによる期待値: 0.4909842816275996
理論上の分散: 0.7599, シミュレーションによる分散: 0.7608618418358614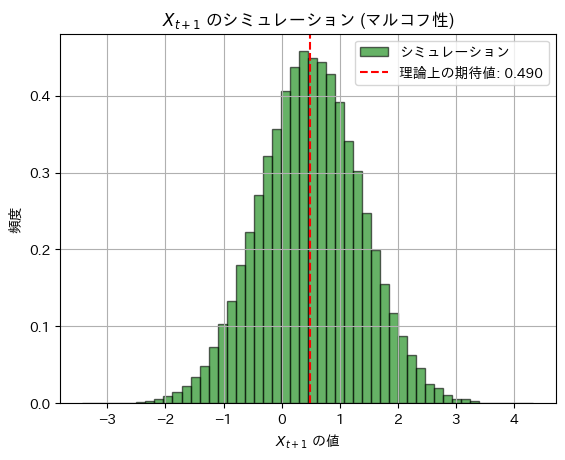
シミュレーション結果は理論値に一致しました。