ホーム » 線形モデル
「線形モデル」カテゴリーアーカイブ
2014 Q3(1)
液体のサンプルの体積と重さから比重がβ0であるという検定を体積と重さの分散が既知の場合と未知の場合でそれぞれ方式を求めました。

コード
帰無仮説![]() の下で、真の値
の下で、真の値![]() が仮説と一致する場合(
が仮説と一致する場合(![]() )と異なる場合(
)と異なる場合(![]() )におけるZ検定とT検定の棄却率を比較します。
)におけるZ検定とT検定の棄却率を比較します。
# 2014 Q3(1) 2025.1.5 (2025.1.6修正)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, t
# Parameters
n = 30 # サンプルサイズ
beta_0 = 1.2 # 仮説のβ
sigma_X = 1.0 # Xの標準偏差
sigma_Y = 3.0 # Yの標準偏差
mu_X = 5.0 # Xの平均 (十分大きく設定)
alpha = 0.05 # 有意水準
num_simulations = 1000 # シミュレーション回数
# 分散の妥当性を確認
beta_true_values = [1.2, 1.5] # 真のβの候補
# 結果を格納するリスト
simulated_Z_dict = {}
simulated_T_dict = {}
rejection_rates_Z = {}
rejection_rates_T = {}
for beta_true in beta_true_values:
if sigma_Y**2 <= (beta_true * sigma_X)**2:
raise ValueError(f"sigma_Y^2は(beta_true * sigma_X)^2より大きくなければなりません (beta_true={beta_true})。")
# 誤差項の分散を計算
sigma_epsilon_squared = sigma_Y**2 + (beta_true * sigma_X)**2
# Z統計量とT統計量を格納するリスト
simulated_Z = []
simulated_T = []
reject_count_Z = 0
reject_count_T = 0
for _ in range(num_simulations):
# Xを正規分布で生成
X = np.random.normal(mu_X, sigma_X, n) # 平均mu_X、標準偏差sigma_X
epsilon = np.random.normal(0, np.sqrt(sigma_epsilon_squared), n) # 誤差項
# Yを生成
Y = beta_true * X + epsilon
# Z検定 (分散既知)
X_bar = np.mean(X)
Y_bar = np.mean(Y)
Z = (Y_bar - beta_0 * X_bar) / np.sqrt((sigma_Y**2 + beta_0**2 * sigma_X**2) / n)
simulated_Z.append(Z)
if abs(Z) > norm.ppf(1 - alpha / 2): # 両側検定
reject_count_Z += 1
# T検定 (分散未知)
U = Y - beta_0 * X
U_bar = np.mean(U)
S_square = np.sum((U - U_bar)**2) / (n - 1)
T = (Y_bar - beta_0 * X_bar) / np.sqrt(S_square / n)
simulated_T.append(T)
if abs(T) > t.ppf(1 - alpha / 2, df=n - 1): # 両側検定
reject_count_T += 1
simulated_Z_dict[beta_true] = simulated_Z
simulated_T_dict[beta_true] = simulated_T
rejection_rates_Z[beta_true] = reject_count_Z / num_simulations
rejection_rates_T[beta_true] = reject_count_T / num_simulations
# 棄却率を表示
print("検定条件: H0: β = 1.2")
for beta_true in beta_true_values:
print(f"真のβ = {beta_true}: Z検定の棄却率 = {rejection_rates_Z[beta_true]:.4f}, T検定の棄却率 = {rejection_rates_T[beta_true]:.4f}")
# グラフ用の範囲を定義
x_values = np.linspace(-4, 4, 1000)
# 理論的なZ分布 (帰無仮説H0: beta = beta_0)
z_pdf = norm.pdf(x_values, 0, 1)
# Z分布のプロット
plt.figure(figsize=(12, 6))
plt.plot(x_values, z_pdf, label="理論分布 (H0: 標準正規分布)", color='blue')
for beta_true, simulated_Z in simulated_Z_dict.items():
plt.hist(simulated_Z, bins=30, density=True, alpha=0.6, label=f"シミュレーション (真のβ = {beta_true})")
plt.axvline(x=norm.ppf(1 - alpha / 2), color='red', linestyle='dashed', label=f"有意水準の境界 (+{norm.ppf(1 - alpha / 2):.2f})")
plt.axvline(x=-norm.ppf(1 - alpha / 2), color='red', linestyle='dashed', label=f"有意水準の境界 (-{norm.ppf(1 - alpha / 2):.2f})")
plt.title("Z分布: 理論分布とシミュレーションの比較 (真のβの変化)", fontsize=16)
plt.xlabel("Z値", fontsize=12)
plt.ylabel("密度", fontsize=12)
plt.legend()
plt.grid()
plt.show()
# 理論的なT分布 (帰無仮説H0: beta = beta_0)
t_pdf = t.pdf(x_values, df=n - 1)
# T分布のプロット
plt.figure(figsize=(12, 6))
plt.plot(x_values, t_pdf, label=f"理論分布 (H0: t分布, 自由度={n - 1})", color='blue')
for beta_true, simulated_T in simulated_T_dict.items():
plt.hist(simulated_T, bins=30, density=True, alpha=0.6, label=f"シミュレーション (真のβ = {beta_true})")
plt.axvline(x=t.ppf(1 - alpha / 2, df=n - 1), color='red', linestyle='dashed', label=f"有意水準の境界 (+{t.ppf(1 - alpha / 2, df=n - 1):.2f})")
plt.axvline(x=-t.ppf(1 - alpha / 2, df=n - 1), color='red', linestyle='dashed', label=f"有意水準の境界 (-{t.ppf(1 - alpha / 2, df=n - 1):.2f})")
plt.title("T分布: 理論分布とシミュレーションの比較 (真のβの変化)", fontsize=16)
plt.xlabel("T値", fontsize=12)
plt.ylabel("密度", fontsize=12)
plt.legend()
plt.grid()
plt.show()検定条件: H0: β = 1.2
真のβ = 1.2: Z検定の棄却率 = 0.0390, T検定の棄却率 = 0.0400
真のβ = 1.5: Z検定の棄却率 = 0.7080, T検定の棄却率 = 0.6490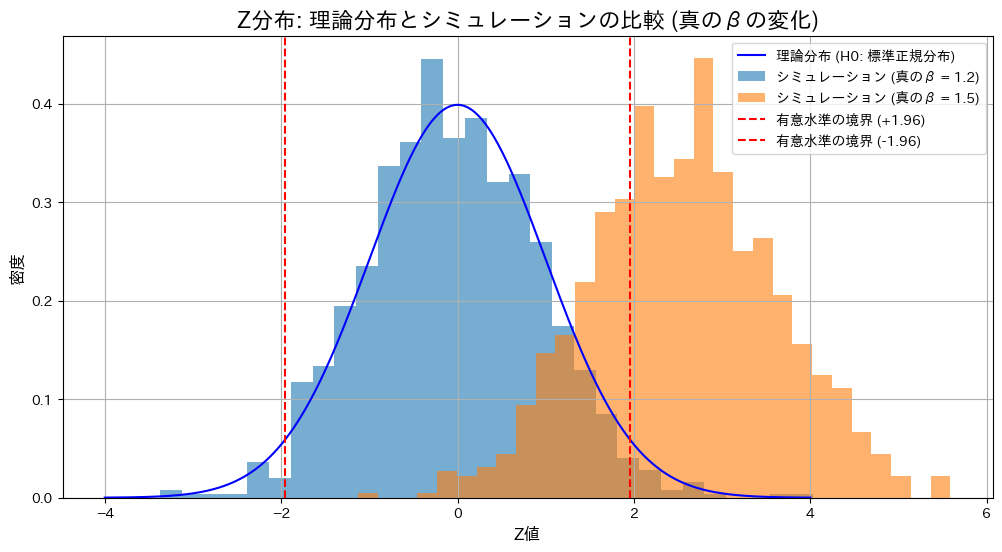
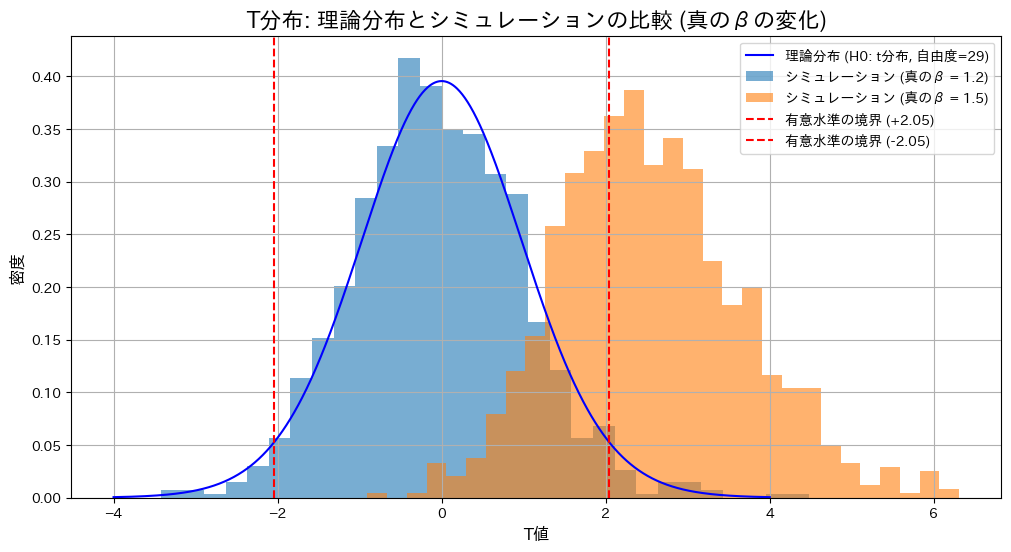
帰無仮説が正しい場合(![]() )、Z検定とT検定の棄却率は有意水準付近で期待通りの結果を示しました。一方、真の値が異なる場合(
)、Z検定とT検定の棄却率は有意水準付近で期待通りの結果を示しました。一方、真の値が異なる場合(![]() )、両検定で棄却域が大幅に上昇し、帰無仮説を適切に棄却できていることが確認されました。また、真の値が異なる場合には、Z検定の棄却率がT検定をわずかに上回る結果となりました。これは、分散既知の場合のZ検定が分散未知のT検定に比べて統計量の推定が安定しているためと考えられます。
)、両検定で棄却域が大幅に上昇し、帰無仮説を適切に棄却できていることが確認されました。また、真の値が異なる場合には、Z検定の棄却率がT検定をわずかに上回る結果となりました。これは、分散既知の場合のZ検定が分散未知のT検定に比べて統計量の推定が安定しているためと考えられます。
2015 Q3(4)
重回帰モデルの重みの2種類の推定量のMSEを求め比較しました。

コード
![]() を
を ![]() と
と ![]() の変化に対してプロットし、その符号の変化を確認します。
の変化に対してプロットし、その符号の変化を確認します。
# 2015 Q3(4) 2024.12.16
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
r12_squared_vals = np.linspace(0, 0.99, 50) # r12^2の値(0から0.99まで)
beta2_squared_vals = np.linspace(0, 1.5, 50) # β2^2の値(0から1.5まで)
sigma2 = 1 # 誤差分散 σ^2
S11 = 10 # S11の仮定値
S12 = 5 # S12の仮定値
S22 = 15 # S22の仮定値
# グリッド生成
R12_squared, Beta2_squared = np.meshgrid(r12_squared_vals, beta2_squared_vals)
# MSEの差の計算
Var_beta2_hat = (sigma2 / S22) * (1 / (1 - R12_squared)) # Var(β2)
MSE_diff = (S12 / S11)**2 * (Var_beta2_hat - Beta2_squared) # MSEの差
# 3Dプロットの描画
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
# 3Dサーフェスプロット
surf = ax.plot_surface(R12_squared, Beta2_squared, MSE_diff, cmap='coolwarm', edgecolor='none')
# 軸ラベルとタイトル
ax.set_title(r'3Dプロット: $\mathrm{MSE}(\hat{\beta}_1) - \mathrm{MSE}(\tilde{\beta}_1)$ の符号反転', fontsize=14)
ax.set_xlabel(r'$r_{12}^2$ (相関係数の二乗)', fontsize=12)
ax.set_ylabel(r'$\beta_2^2$ (回帰係数の二乗)', fontsize=12)
ax.set_zlabel(r'$\mathrm{MSE}(\hat{\beta}_1) - \mathrm{MSE}(\tilde{\beta}_1)$', fontsize=12)
# カラーバーの追加
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=10, label='MSEの差')
plt.tight_layout()
plt.show()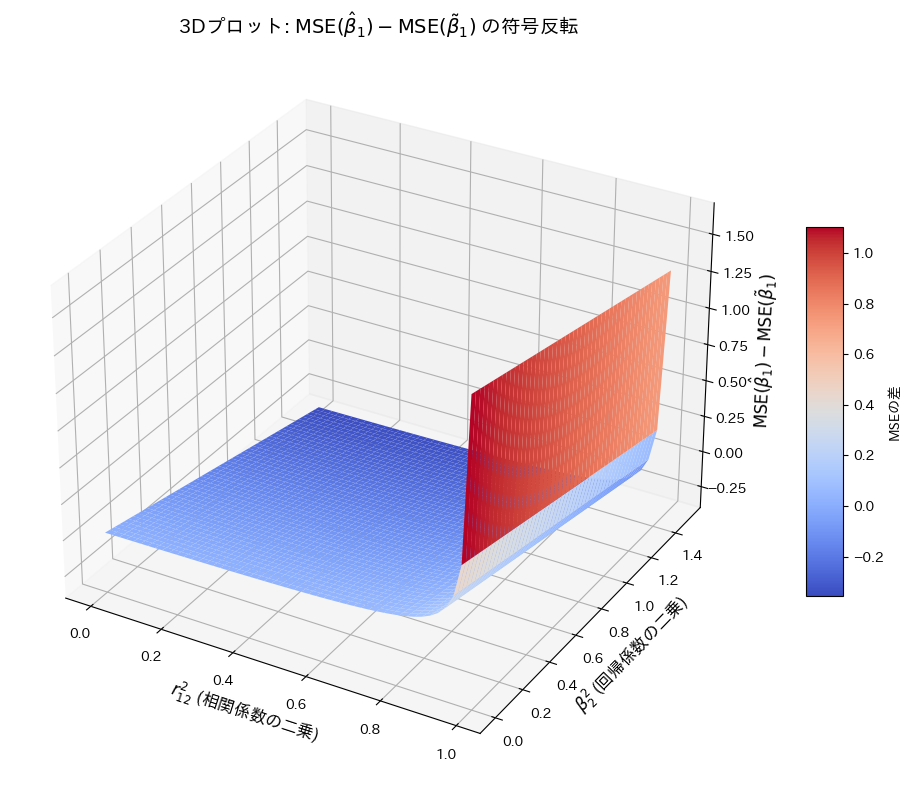
![]() の符号は
の符号は ![]() と
と ![]() の値に依存して変化することが確認できました。
の値に依存して変化することが確認できました。
2015 Q3(4)
重回帰モデルの重みの推定量の分散と、説明変数を減らした時のそれとの差を求め、説明変数間の相関係数によるどのような関数になるのか調べました。

コード
![]() の変化が
の変化が![]() と
と![]() に与える影響を、グラフで描画して確認します。
に与える影響を、グラフで描画して確認します。
# 2015 Q3(4) 2024.12.15
import numpy as np
import matplotlib.pyplot as plt
# 1. パラメータ設定
r12_vals = np.linspace(-0.99, 0.99, 200) # r12の値(-0.99から0.99まで)
sigma2 = 1 # 分散 σ^2
S11 = 10 # S11の仮定値
# 重回帰と単回帰の分散計算
Var_beta1_hat = (sigma2 / S11) * (1 / (1 - r12_vals**2)) # 重回帰(r12に依存)
Var_beta1_tilde = sigma2 / S11 # 単回帰(r12=0の分散)
# 2. グラフのプロット
plt.figure(figsize=(10, 6))
plt.plot(r12_vals, Var_beta1_hat, label=r'$\mathrm{Var}(\hat{\beta}_1)$ (重回帰)', color='blue', linewidth=2)
plt.axhline(y=Var_beta1_tilde, color='orange', linestyle='--', label=r'$\mathrm{Var}(\tilde{\beta}_1)$ (単回帰, $r_{12}=0$)')
# 軸ラベルとタイトル
plt.title(r'$\mathrm{Var}(\tilde{\beta}_1)$ と $\mathrm{Var}(\hat{\beta}_1)$ の比較', fontsize=14, fontweight='bold')
plt.xlabel(r'$r_{12}$($x_1$と$x_2$の相関)', fontsize=12)
plt.ylabel(r'分散', fontsize=12)
# 凡例とグリッド
plt.legend(fontsize=10, loc='upper right')
plt.grid(alpha=0.5)
# グラフ表示
plt.tight_layout()
plt.show()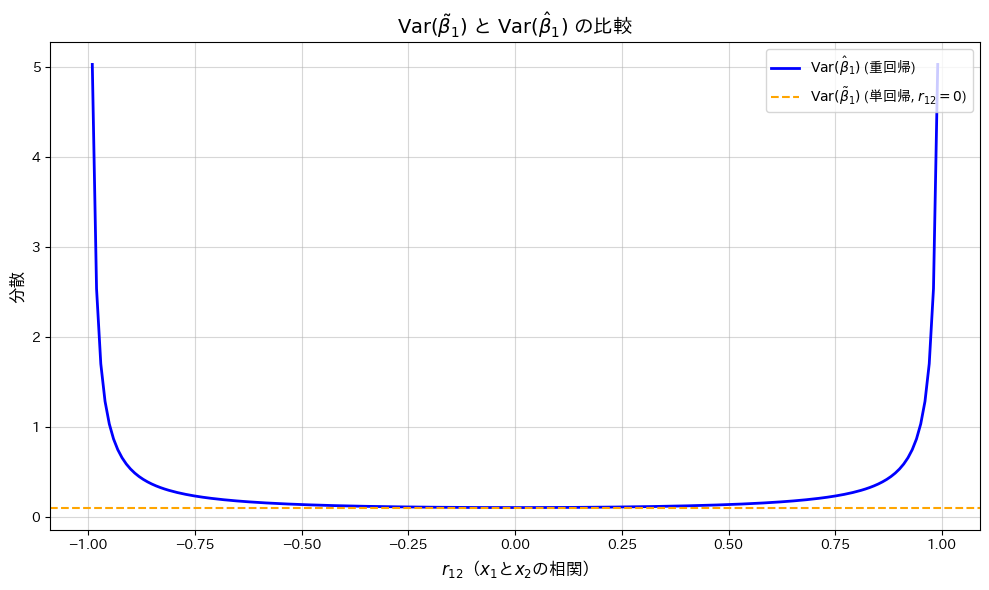
![]() が0に近いほど
が0に近いほど![]() は最小となり、相関が高まると分散が増加する一方で、
は最小となり、相関が高まると分散が増加する一方で、![]() は一定であることが確認されました。
は一定であることが確認されました。
次に、横軸を![]() として、
として、![]() と
と![]() の変化をプロットし、両者の差も併せて確認します。
の変化をプロットし、両者の差も併せて確認します。
# 2015 Q3(4) 2024.12.15
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
r12_vals = np.linspace(-0.99, 0.99, 200) # r12の値(-0.99から0.99まで)
sigma2 = 1 # 分散 σ^2
S11 = 10 # S11の仮定値
# r12^2 の計算
r12_squared_vals = r12_vals**2 # r12^2 の値
# 重回帰と単回帰の分散計算
Var_beta1_hat = (sigma2 / S11) * (1 / (1 - r12_squared_vals)) # 重回帰(r12に依存)
Var_beta1_tilde = sigma2 / S11 # 単回帰(r12=0の分散)
# 分散の差の計算
Var_diff = Var_beta1_hat - Var_beta1_tilde # 分散の差
# グラフのプロット
plt.figure(figsize=(10, 6))
# 分散のプロット
plt.plot(r12_squared_vals, Var_beta1_hat, label=r'$\mathrm{Var}(\hat{\beta}_1)$ (重回帰)', color='blue', linewidth=2)
plt.axhline(y=Var_beta1_tilde, color='orange', linestyle='--', label=r'$\mathrm{Var}(\tilde{\beta}_1)$ (単回帰, $r_{12}=0$)')
# 分散の差をプロット
plt.plot(r12_squared_vals, Var_diff, label=r'$\mathrm{Var}(\hat{\beta}_1) - \mathrm{Var}(\tilde{\beta}_1)$', color='green', linewidth=2, linestyle=':')
# 軸ラベルとタイトル
plt.title(r'$\mathrm{Var}(\tilde{\beta}_1)$, $\mathrm{Var}(\hat{\beta}_1)$ とその差の比較 ($r_{12}^2$)', fontsize=14, fontweight='bold')
plt.xlabel(r'$r_{12}^2$(相関係数の二乗)', fontsize=12)
plt.ylabel(r'分散 / 差', fontsize=12)
# 凡例とグリッド
plt.legend(fontsize=10, loc='upper right')
plt.grid(alpha=0.5)
# グラフ表示
plt.tight_layout()
plt.show()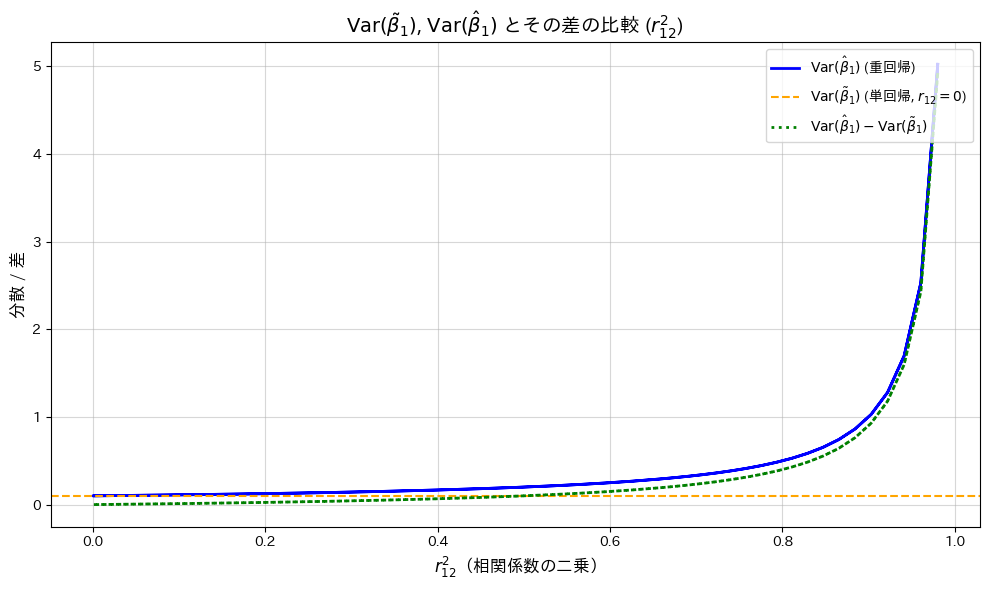
![]() が
が![]() の単調増加関数であることが確認されました。
の単調増加関数であることが確認されました。
2015 Q3(3)
重回帰モデルの重みの推定量の分散を求め、説明変数間の相関がそれにどのように影響するか確認しました。
コード
![]() の変化が
の変化が![]() と
と![]() に与える影響を、グラフで描画して確認します。
に与える影響を、グラフで描画して確認します。
# 2015 Q3(3) 2024.12.14
import numpy as np
import matplotlib.pyplot as plt
# 1. パラメータ設定
r12_vals = np.linspace(-0.99, 0.99, 200) # r12の値(-0.99から0.99まで)
sigma2 = 1 # 分散 σ^2
S11 = 10 # S11の仮定値
S22 = 15 # S22の仮定値
# 2. 分散の計算
Var_beta1 = (sigma2 / S11) * (1 / (1 - r12_vals**2)) # Var(β1)
Var_beta2 = (sigma2 / S22) * (1 / (1 - r12_vals**2)) # Var(β2)
# 3. グラフのプロット
plt.figure(figsize=(10, 6))
plt.plot(r12_vals, Var_beta1, label=r'$\mathrm{Var}(\hat{\beta}_1)$', color='blue', linewidth=2)
plt.plot(r12_vals, Var_beta2, label=r'$\mathrm{Var}(\hat{\beta}_2)$', color='orange', linewidth=2)
plt.axhline(y=sigma2 / S11, color='blue', linestyle='--', label=r'$r_{12}=0$ の $\mathrm{Var}(\hat{\beta}_1)$')
plt.axhline(y=sigma2 / S22, color='orange', linestyle='--', label=r'$r_{12}=0$ の $\mathrm{Var}(\hat{\beta}_2)$')
# 軸ラベルとタイトル
plt.title(r'$\mathrm{Var}(\hat{\beta}_1)$ と $\mathrm{Var}(\hat{\beta}_2)$ の $r_{12}$ に対する変化', fontsize=14, fontweight='bold')
plt.xlabel(r'$r_{12}$($x_1$と$x_2$の相関)', fontsize=12)
plt.ylabel(r'分散', fontsize=12)
# 凡例とグリッド
plt.legend(fontsize=10, loc='upper right')
plt.grid(alpha=0.5)
# グラフ表示
plt.tight_layout()
plt.show()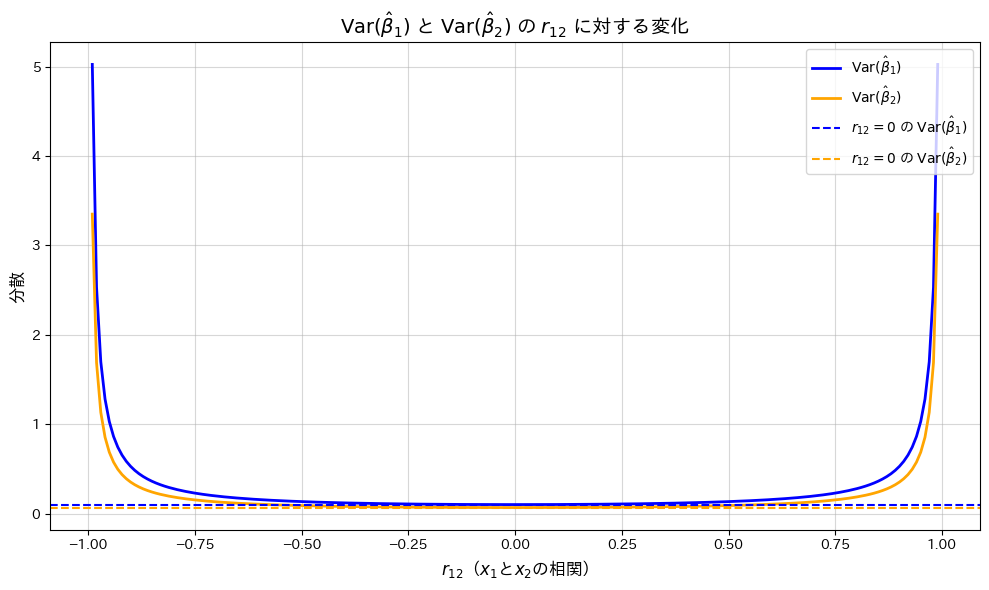
![]() が0に近いほど
が0に近いほど![]() と
と![]() は最小となり、相関が高まると分散が増加することが確認されました。
は最小となり、相関が高まると分散が増加することが確認されました。
2015 Q3(2)
重回帰モデルの重みβ1を3つの相関係数を使って表し、それが負になる必要十分条件を求めました。
コード
![]() が大きな値をとる場合、
が大きな値をとる場合、![]() が負の値をとりやすくなることを確認するため、
が負の値をとりやすくなることを確認するため、![]() と
と![]() は、正の数に固定した上で、グラフで可視化します。
は、正の数に固定した上で、グラフで可視化します。
# 2015 Q3(2) 2024.12.13
import numpy as np
import matplotlib.pyplot as plt
# 1. パラメータの設定
n = 100 # サンプルサイズ
r12_vals = np.linspace(-0.99, 0.99, 100) # r12 を -0.99 から 0.99 まで変化させる
r1y = 0.5 # r1y を固定
r2y = 0.6 # r2y を固定
# 2. Beta1 の計算
beta1_vals = []
for r12 in r12_vals:
if abs(r12) >= 1:
beta1_vals.append(np.nan) # r12 = ±1 の場合は計算不能
continue
beta1 = (r1y - r12 * r2y) / (1 - r12**2) # 簡略化された Beta1 の符号条件
beta1_vals.append(beta1)
# 3. 結果の可視化
plt.figure(figsize=(8, 6))
plt.plot(r12_vals, beta1_vals, label=r'$\hat{\beta}_1$', color='blue')
plt.axhline(0, color='red', linestyle='--', label='ゼロライン (基準)')
plt.title(r'$\hat{\beta}_1$ と $r_{12}$ の関係', fontsize=14, fontweight='bold')
plt.xlabel(r'$r_{12}$($x_1$と$x_2$の相関)', fontsize=12)
plt.ylabel(r'$\hat{\beta}_1$', fontsize=12)
plt.legend(fontsize=10, loc='upper left')
plt.grid(alpha=0.7)
plt.tight_layout()
plt.show()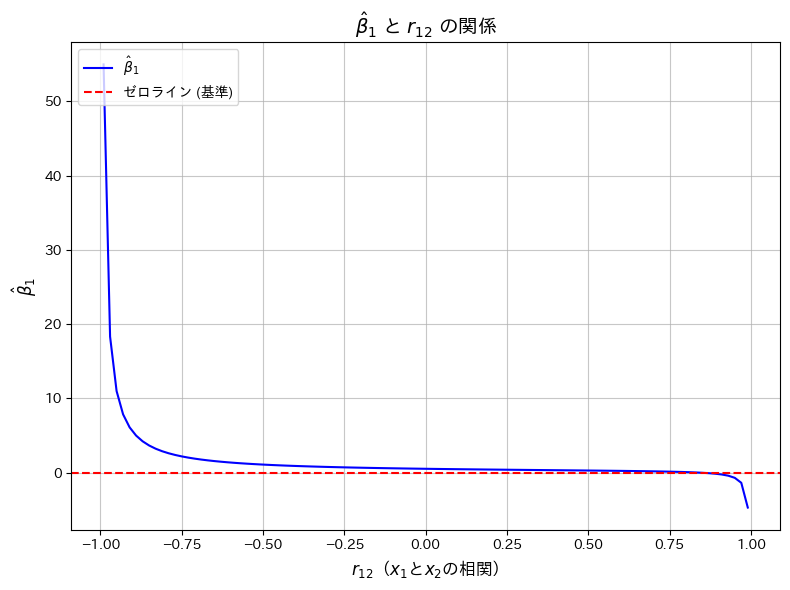
![]() が1に近い値をとると、
が1に近い値をとると、![]() が負の値をとる傾向があることが確認できました。
が負の値をとる傾向があることが確認できました。
2015 Q3(1)
重回帰モデルにおいて正規方程式を用い、各重みの最小二乗推定量を求めました。
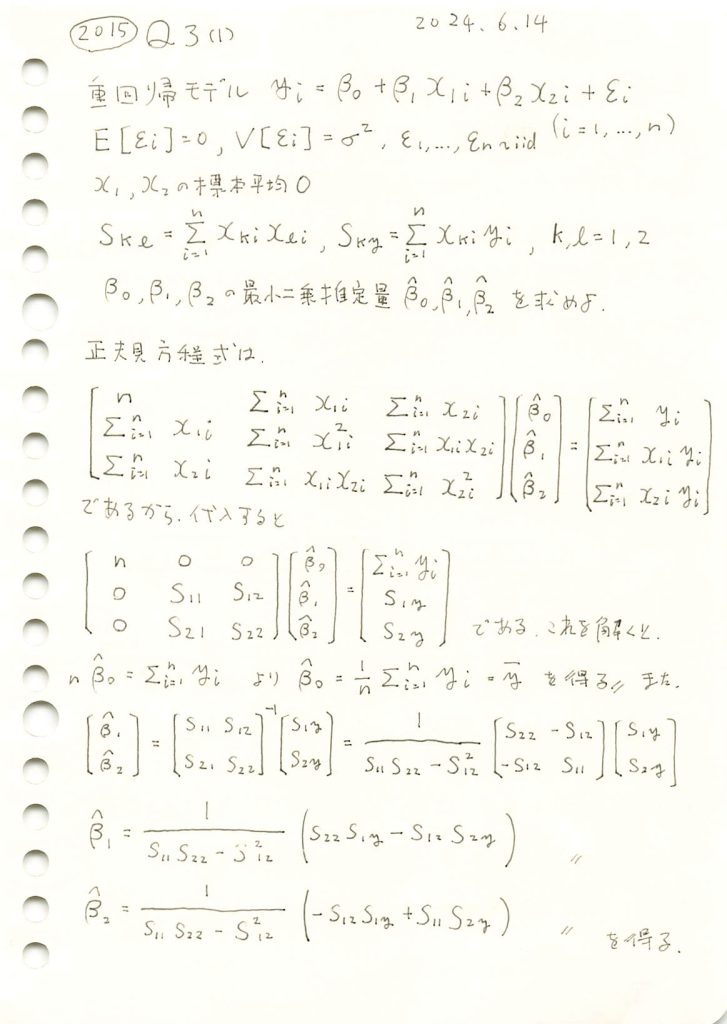
コード
重回帰モデルのシミュレーションを行い、パラメータβ0,β1,β2の推定量を計算し、真の値と比較します。
# 2015 Q3(1) 2024.12.12
import numpy as np
# 1. パラメータの設定 (再現性のため同じ設定を使用)
n = 100
beta_0, beta_1, beta_2 = 2.0, 1.0, -0.5
sigma = 1.0
# 2. 説明変数と誤差の生成
x1 = np.random.randn(n)
x2 = np.random.randn(n)
epsilon = np.random.randn(n) * sigma
# 3. 応答変数の生成
y = beta_0 + beta_1 * x1 + beta_2 * x2 + epsilon
# 4. S11, S22, S12, S1y, S2y を計算
S11 = np.sum(x1**2)
S22 = np.sum(x2**2)
S12 = np.sum(x1 * x2)
S1y = np.sum(x1 * y)
S2y = np.sum(x2 * y)
# 5. 推定値の計算 (導出した式に基づく)
denominator = S11 * S22 - S12**2
beta1_hat = (S22 * S1y - S12 * S2y) / denominator
beta2_hat = (S11 * S2y - S12 * S1y) / denominator
beta0_hat = np.mean(y) - beta1_hat * np.mean(x1) - beta2_hat * np.mean(x2)
# 推定値の表示
print(f"推定値 (導出した式):")
print(f" β0 = {beta0_hat:.3f}")
print(f" β1 = {beta1_hat:.3f}")
print(f" β2 = {beta2_hat:.3f}")
# 真の値と比較
print("\n真の値:")
print(f" β0 = {beta_0:.3f}")
print(f" β1 = {beta_1:.3f}")
print(f" β2 = {beta_2:.3f}")推定値 (導出した式):
β0 = 1.909
β1 = 0.863
β2 = -0.505
真の値:
β0 = 2.000
β1 = 1.000
β2 = -0.500シミュレーションの結果、パラメータβ0,β1,β2の推定量はわずかな誤差はあるものの、真の値に近い値を示しました。
2016 Q3(3)
線形モデルの未知の母数βの3つの不偏推定量の各分散の大小関係を求めました。
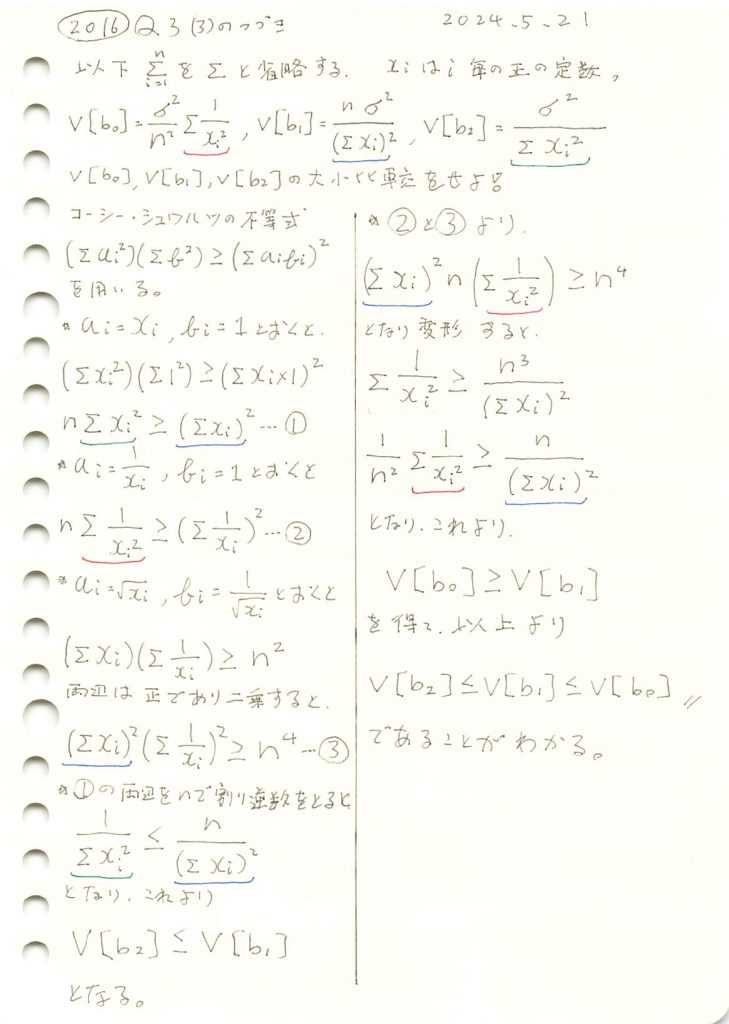
コード
線形モデルのパラメータβの推定量b0,b1,b2の分散の違いを理論式に基づいて確認します。説明変数xiには一様分布に従う値を与え、サンプル数nを変化させて、各推定量の分散の変化を視覚的に比較してみます。ここでは各推定量の違いが分かりやすいように、分散の代わりに標準偏差を視覚化しています。詳しくは前記事(https://statistics.blue/2016-q33/)を参照。
# 2016 Q3(3) 2024.11.22
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 1 # 誤差の標準偏差
true_beta = 2 # 真のβ
sample_sizes = np.arange(10, 101, 10) # サンプルサイズ n を 10 から 100 まで 10 刻みで変化
# 理論的な分散を格納するリスト
variances_b0 = []
variances_b1 = []
variances_b2 = []
# 各サンプルサイズ n に対して分散を計算
for n in sample_sizes:
xi = np.arange(1, n + 1) # 一様に分布した x_i を生成 (例: 1, 2, ..., n)
sum_xi = np.sum(xi)
sum_xi_squared = np.sum(xi**2)
sum_1_over_xi_squared = np.sum(1 / xi**2)
# 分散を理論式で計算
V_b0 = (sigma**2 / n**2) * sum_1_over_xi_squared
V_b1 = (sigma**2 * n) / (sum_xi**2)
V_b2 = sigma**2 / sum_xi_squared
variances_b0.append(V_b0)
variances_b1.append(V_b1)
variances_b2.append(V_b2)
# 理論値からの標準偏差として各分散の平方根を計算
std_b0 = np.sqrt(variances_b0)
std_b1 = np.sqrt(variances_b1)
std_b2 = np.sqrt(variances_b2)
# グラフ作成
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, std_b0, label='$|b_0 - \\beta|$ (標準偏差)', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, std_b1, label='$|b_1 - \\beta|$ (標準偏差)', marker='x', linestyle='dashed', color='orange')
plt.plot(sample_sizes, std_b2, label='$|b_2 - \\beta|$ (標準偏差)', marker='s', linestyle='dashed', color='purple')
plt.axhline(y=0, color='green', linestyle='solid', label='真の値 $\\beta = 2$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('真の値からの標準偏差')
plt.title('推定量 $b_0, b_1, b_2$ の真の値からのずれ(標準偏差)')
plt.legend()
plt.grid(True)
plt.show()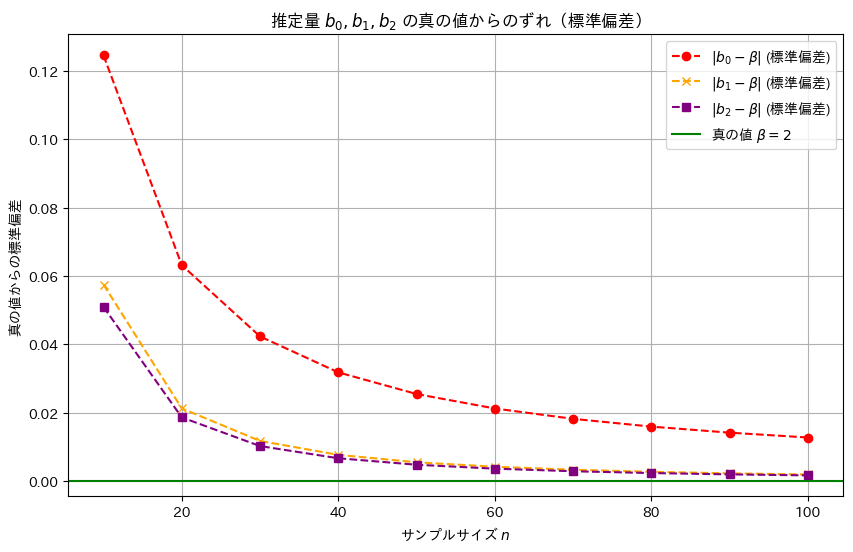
推定量b2,b1,b0の順に標準誤差は小さく、分散も同様の順序で小さくなることが確認できました。この結果から、最小二乗推定量b2が最も効率的であり、推定の安定性が高いことが再確認できました。
2016 Q3(3)
線形モデルの未知の母数βの3つの不偏推定量の各分散を求めました。
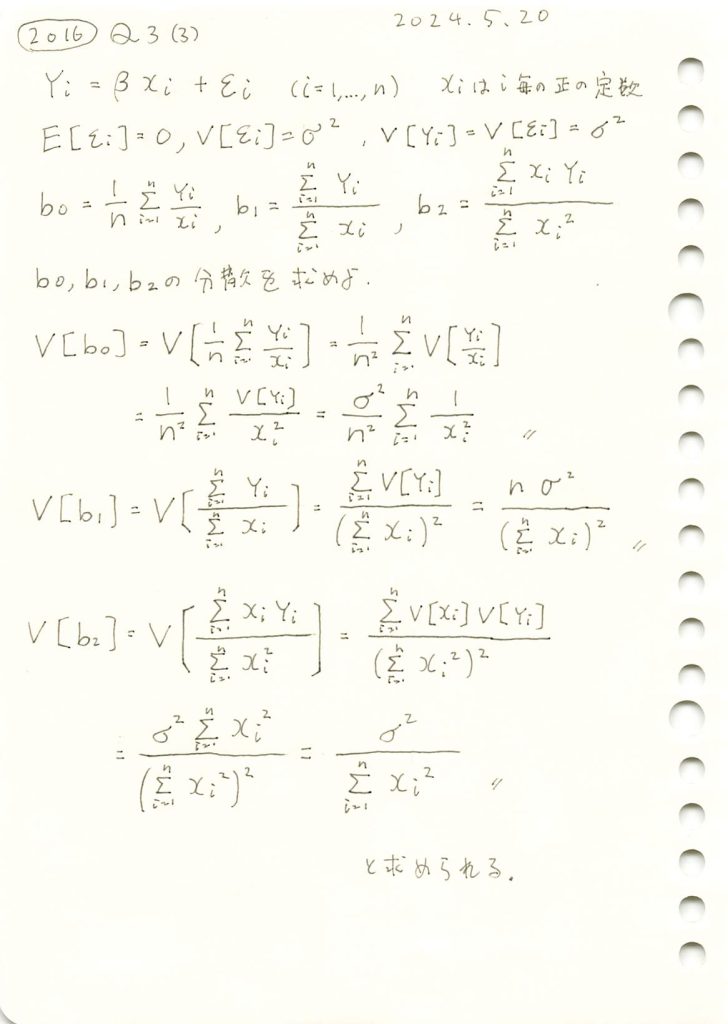
コード
線形モデルのパラメータβの推定量b0,b1,b2の分散の違いを理論式に基づいて確認します。説明変数xiには一様分布に従う値を与え、サンプル数nを変化させて、各推定量の分散の変化を視覚的に比較してみます。
# 2016 Q3(3) 2024.11.22
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 1 # 誤差の標準偏差
sample_sizes = np.arange(10, 101, 10) # サンプルサイズ n を 10 から 100 まで 10 刻みで変化
# 理論的な分散を格納するリスト
variances_b0 = []
variances_b1 = []
variances_b2 = []
# 各サンプルサイズ n に対して分散を計算
for n in sample_sizes:
xi = np.arange(1, n + 1) # 一様に分布した x_i を生成 (例: 1, 2, ..., n)
sum_xi = np.sum(xi)
sum_xi_squared = np.sum(xi**2)
sum_1_over_xi_squared = np.sum(1 / xi**2)
# 分散を理論式で計算
V_b0 = (sigma**2 / n**2) * sum_1_over_xi_squared
V_b1 = (sigma**2 * n) / (sum_xi**2)
V_b2 = sigma**2 / sum_xi_squared
variances_b0.append(V_b0)
variances_b1.append(V_b1)
variances_b2.append(V_b2)
# グラフ作成
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, variances_b0, label='$V[b_0]$', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, variances_b1, label='$V[b_1]$', marker='x', linestyle='dashed', color='orange')
plt.plot(sample_sizes, variances_b2, label='$V[b_2]$', marker='s', linestyle='dashed', color='purple')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('分散')
plt.title('推定量 $b_0$, $b_1$, $b_2$ の理論的分散')
plt.legend()
plt.grid(True)
plt.show()
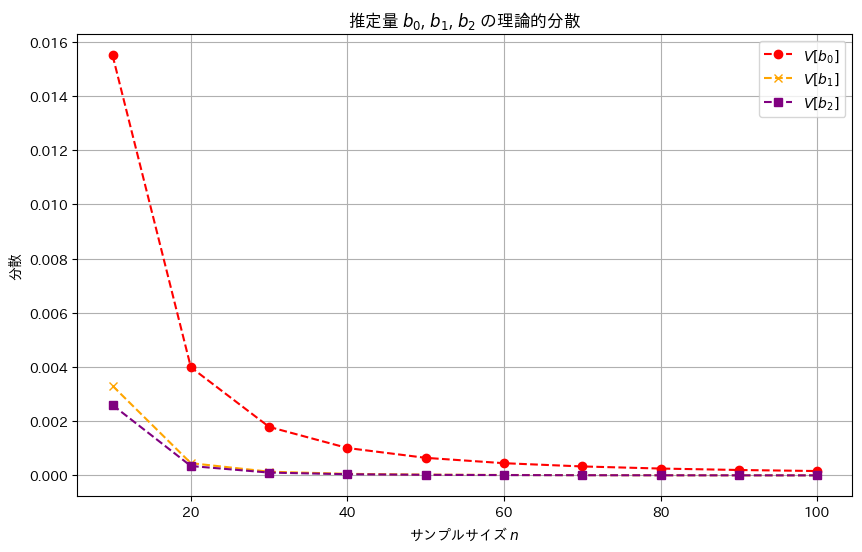
推定量b2,b1,b0の順に分散は小さく見え、b2,b1,b0の順により安定した推定量であることが確認できました。
推定量b1,b2が重なっていて見えづらいため、標準誤差でも視覚化してみます。
# 2016 Q3(3) 2024.11.22
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 1 # 誤差の標準偏差
true_beta = 2 # 真のβ
sample_sizes = np.arange(10, 101, 10) # サンプルサイズ n を 10 から 100 まで 10 刻みで変化
# 理論的な分散を格納するリスト
variances_b0 = []
variances_b1 = []
variances_b2 = []
# 各サンプルサイズ n に対して分散を計算
for n in sample_sizes:
xi = np.arange(1, n + 1) # 一様に分布した x_i を生成 (例: 1, 2, ..., n)
sum_xi = np.sum(xi)
sum_xi_squared = np.sum(xi**2)
sum_1_over_xi_squared = np.sum(1 / xi**2)
# 分散を理論式で計算
V_b0 = (sigma**2 / n**2) * sum_1_over_xi_squared
V_b1 = (sigma**2 * n) / (sum_xi**2)
V_b2 = sigma**2 / sum_xi_squared
variances_b0.append(V_b0)
variances_b1.append(V_b1)
variances_b2.append(V_b2)
# 理論値からの標準偏差として各分散の平方根を計算
std_b0 = np.sqrt(variances_b0)
std_b1 = np.sqrt(variances_b1)
std_b2 = np.sqrt(variances_b2)
# グラフ作成
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, std_b0, label='$|b_0 - \\beta|$ (標準偏差)', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, std_b1, label='$|b_1 - \\beta|$ (標準偏差)', marker='x', linestyle='dashed', color='orange')
plt.plot(sample_sizes, std_b2, label='$|b_2 - \\beta|$ (標準偏差)', marker='s', linestyle='dashed', color='purple')
plt.axhline(y=0, color='green', linestyle='solid', label='真の値 $\\beta = 2$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('真の値からの標準偏差')
plt.title('推定量 $b_0, b_1, b_2$ の真の値からのずれ(標準偏差)')
plt.legend()
plt.grid(True)
plt.show()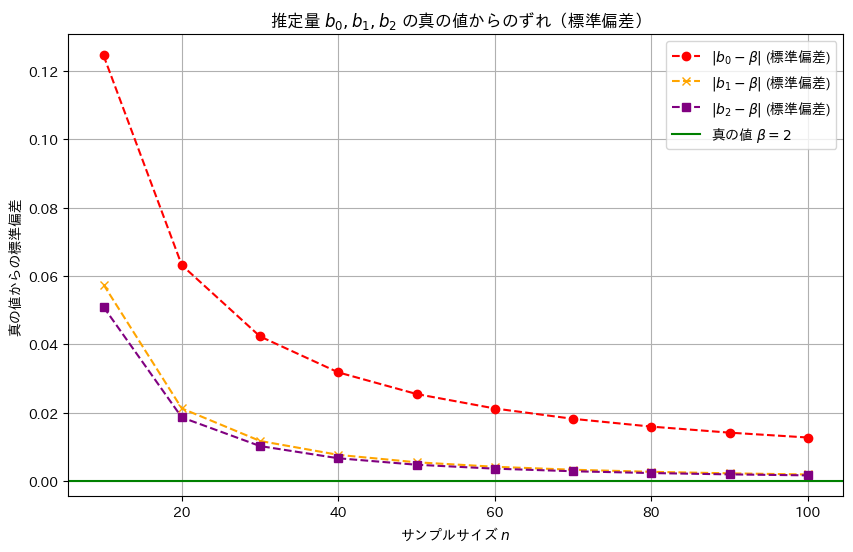
推定量b2,b1,b0の順に標準誤差は小さく、分散も同様の順序で小さくなることが確認できました。この結果から、最小二乗推定量b2が最も効率的であり、推定の安定性が高いことが再確認できました。
2016 Q3(2)
線形モデルの未知の母数βの最小二乗推定量を求め、それが不偏推定量であることを確認しました。
コード
乱数を発生させて線形モデルのパラメータβの推定量b0,b1,b2をそれぞれ計算し、観測データとともにプロットしてみます。推定された直線と真の直線がどのように異なるか視覚的に確認してみます。(b0,b1は前問参照)
# 2016 Q3(2) 2024.11.21
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 10 # サンプルサイズ
true_beta = 2 # 真のβ
sigma = 5 # 誤差の標準偏差
# 1. xi を一様分布から生成
xi = np.random.uniform(1, 10, n)
# 2. εi を正規分布から生成
epsilon_i = np.random.normal(0, sigma, n)
# 3. Yi を計算
Yi = true_beta * xi + epsilon_i
# 4. 推定量 b0, b1 を計算
b0 = np.mean(Yi / xi)
b1 = np.sum(Yi) / np.sum(xi)
# 5. 最小二乗推定量 b2 を計算
b2 = np.sum(xi * Yi) / np.sum(xi**2)
# プロット
plt.figure(figsize=(10, 6))
plt.scatter(xi, Yi, label='観測データ ($Y_i$)', color='blue', marker='x') # マーカーを 'x' に変更
plt.plot(np.sort(xi), true_beta * np.sort(xi), label=f'真の直線 ($\\beta={true_beta}$)', color='green', linestyle='dashed')
plt.plot(np.sort(xi), b0 * np.sort(xi), label=f'推定直線 ($b_0={b0:.2f}$)', color='red')
plt.plot(np.sort(xi), b1 * np.sort(xi), label=f'推定直線 ($b_1={b1:.2f}$)', color='orange')
plt.plot(np.sort(xi), b2 * np.sort(xi), label=f'推定直線 ($b_2={b2:.2f}$)', color='purple')
plt.xlabel('$x_i$')
plt.ylabel('$Y_i$')
plt.title('線形モデルの推定')
plt.legend()
plt.grid(True)
plt.show()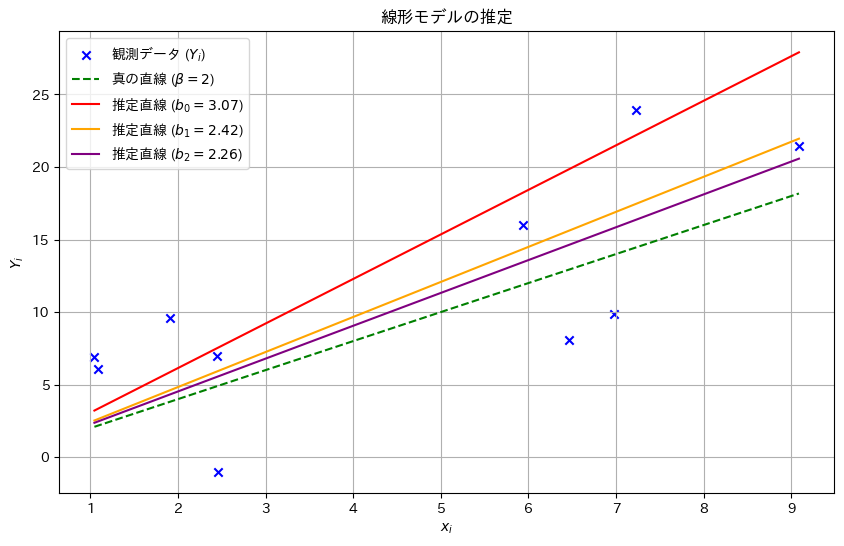
推定量b2,b1,b0の順に真のβに近い値を取りました。
次に、サンプル数nを変化させて、推定量b0,b1,b2がどのように変化するのか観察します
# 2016 Q3(2) 2024.11.21
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 5 # 誤差の標準偏差
true_beta = 2 # 真のβ
sample_sizes = np.arange(5, 101, 5) # n を 5 から 100 まで 5 刻みで変化
simulations = 1000 # 各 n に対してのシミュレーション回数
b0_means = []
b1_means = []
b2_means = [] # b2 の期待値を記録
# 各サンプルサイズ n に対してシミュレーションを実行
for n in sample_sizes:
b0_samples = []
b1_samples = []
b2_samples = [] # b2 を記録
for _ in range(simulations):
xi = np.random.uniform(1, 10, n)
epsilon_i = np.random.normal(0, sigma, n)
Yi = true_beta * xi + epsilon_i
b0_samples.append(np.mean(Yi / xi))
b1_samples.append(np.sum(Yi) / np.sum(xi))
b2_samples.append(np.sum(xi * Yi) / np.sum(xi**2)) # b2 を計算
b0_means.append(np.mean(b0_samples))
b1_means.append(np.mean(b1_samples))
b2_means.append(np.mean(b2_samples)) # b2 の期待値を記録
# 結果をプロット
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, b0_means, label='$b_0$の期待値', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, b1_means, label='$b_1$の期待値', marker='x', linestyle='dashed', color='orange')
plt.plot(sample_sizes, b2_means, label='$b_2$の期待値', marker='s', linestyle='dashed', color='purple') # b2 を追加
plt.axhline(y=true_beta, color='green', linestyle='solid', label='真の値 $\\beta=2$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('推定量の期待値')
plt.title('推定量 $b_0, b_1, b_2$ の期待値とサンプルサイズの関係')
plt.legend()
plt.grid(True)
plt.show()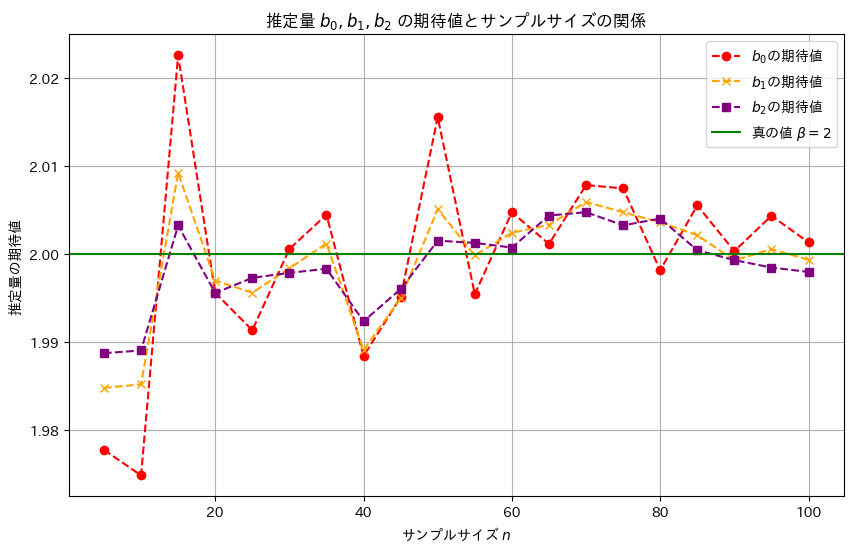
サンプルサイズnが大きくなるほど、推定量b0,b1,b2は真の値βに近づくことが確認できました。また、推定量b2,b1,b0の順に分散は小さく見え、b2,b1,b0の順により安定した推定量のようです。
次に、推定量b0,b1,b2の分布を確認してみます。それぞれのヒストグラムを重ねて表示してみます。
# 2016 Q3(2) 2024.11.21
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 100 # サンプルサイズ
true_beta = 2 # 真のβ
sigma = 1 # 誤差の標準偏差
simulations = 10000 # シミュレーション回数
b0_samples = []
b1_samples = []
b2_samples = [] # b2 の分布を記録
# シミュレーションを実施
for _ in range(simulations):
xi = np.random.uniform(1, 10, n)
epsilon_i = np.random.normal(0, sigma, n)
Yi = true_beta * xi + epsilon_i
b0_samples.append(np.mean(Yi / xi))
b1_samples.append(np.sum(Yi) / np.sum(xi))
b2_samples.append(np.sum(xi * Yi) / np.sum(xi**2)) # b2 を計算
# b0, b1, b2 の分布を重ねてプロット
plt.figure(figsize=(10, 6))
plt.hist(b0_samples, bins=30, density=True, color='red', alpha=0.5, label='$b_0$')
plt.hist(b1_samples, bins=30, density=True, color='orange', alpha=0.5, label='$b_1$')
plt.hist(b2_samples, bins=30, density=True, color='purple', alpha=0.5, label='$b_2$') # b2 を追加
plt.axvline(x=true_beta, color='green', linestyle='dashed', label='真の値 $\\beta=2$')
plt.title('$b_0$, $b_1$, $b_2$ の分布 (n=100)')
plt.xlabel('推定値')
plt.ylabel('頻度')
plt.legend()
plt.grid(True)
plt.show()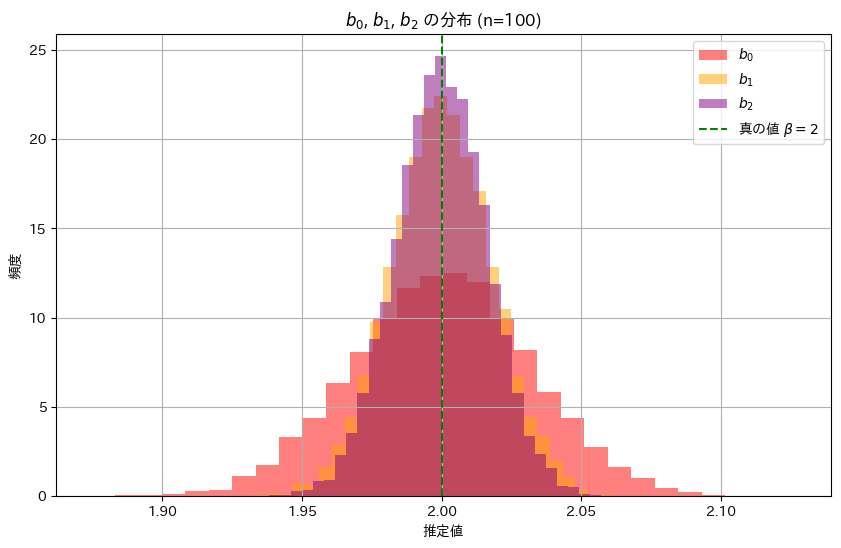
推定量b2,b1,b0の順に幅が狭く、分散が小さいことが確認できました。これにより推定量b2,b1,b0の順に安定した推定であることが分かりました。
2016 Q3(1)
線形モデルの未知の母数βの2つの推定量が不偏推定量であることを確認しました。

コード
乱数を発生させて線形モデルのパラメータβの推定量b0,b1をそれぞれ求め、観測データとともにプロットしてみます。推定された直線と真の直線がどのように異なるか視覚的に確認してみます。
# 2016 Q3(1) 2024.11.20
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 50 # サンプルサイズ
true_beta = 2 # 真のβ
sigma = 5 # 誤差の標準偏差
# 1. xi を一様分布から生成
xi = np.random.uniform(1, 10, n)
# 2. εi を正規分布から生成
epsilon_i = np.random.normal(0, sigma, n)
# 3. Yi を計算
Yi = true_beta * xi + epsilon_i
# 4. 推定量 b0, b1 を計算
b0 = np.mean(Yi / xi)
b1 = np.sum(Yi) / np.sum(xi)
# プロット
plt.figure(figsize=(10, 6))
plt.scatter(xi, Yi, label='観測データ ($Y_i$)', color='blue', marker='x')
plt.plot(np.sort(xi), true_beta * np.sort(xi), label=f'真の直線 ($\\beta={true_beta}$)', color='green', linestyle='dashed')
plt.plot(np.sort(xi), b0 * np.sort(xi), label=f'推定直線 ($b_0={b0:.2f}$)', color='red')
plt.plot(np.sort(xi), b1 * np.sort(xi), label=f'推定直線 ($b_1={b1:.2f}$)', color='orange')
plt.xlabel('$x_i$')
plt.ylabel('$Y_i$')
plt.title('線形モデルの推定')
plt.legend()
plt.grid(True)
plt.show()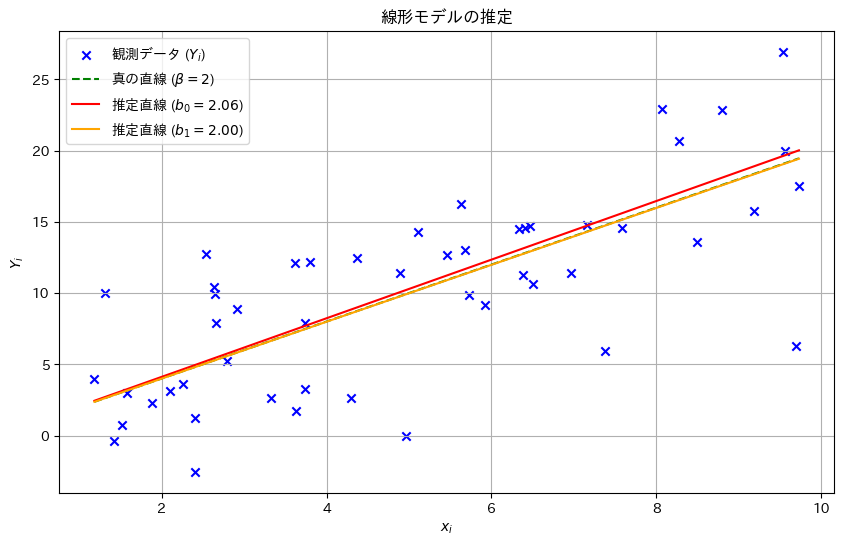
b0とb1は真のβに近い値を取り、直線は概ね一致しました。
次に、サンプル数nを変化させて、推定量b0,b1がどのように変化するのか観察します
# 2016 Q3(1) 2024.11.20
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 50 # サンプルサイズ
true_beta = 2 # 真のβ
sigma = 5 # 誤差の標準偏差
# サンプルサイズを変化させて b0, b1 の期待値を検証
sample_sizes = np.arange(5, 101, 5) # n を 5 から 100 まで 5 刻みで変化
true_beta = 2 # 真のβ
simulations = 1000 # 各 n に対してのシミュレーション回数
b0_means = []
b1_means = []
# 各サンプルサイズ n に対してシミュレーションを実行
for n in sample_sizes:
b0_samples = []
b1_samples = []
for _ in range(simulations):
xi = np.random.uniform(1, 10, n)
epsilon_i = np.random.normal(0, sigma, n)
Yi = true_beta * xi + epsilon_i
b0_samples.append(np.mean(Yi / xi))
b1_samples.append(np.sum(Yi) / np.sum(xi))
b0_means.append(np.mean(b0_samples))
b1_means.append(np.mean(b1_samples))
# 結果をプロット
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, b0_means, label='$b_0$の期待値', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, b1_means, label='$b_1$の期待値', marker='x', linestyle='dashed', color='orange')
plt.axhline(y=true_beta, color='green', linestyle='solid', label='真の値 $\\beta=2$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('推定量の期待値')
plt.title('推定量 $b_0, b_1$ の期待値とサンプルサイズの関係')
plt.legend()
plt.grid(True)
plt.show()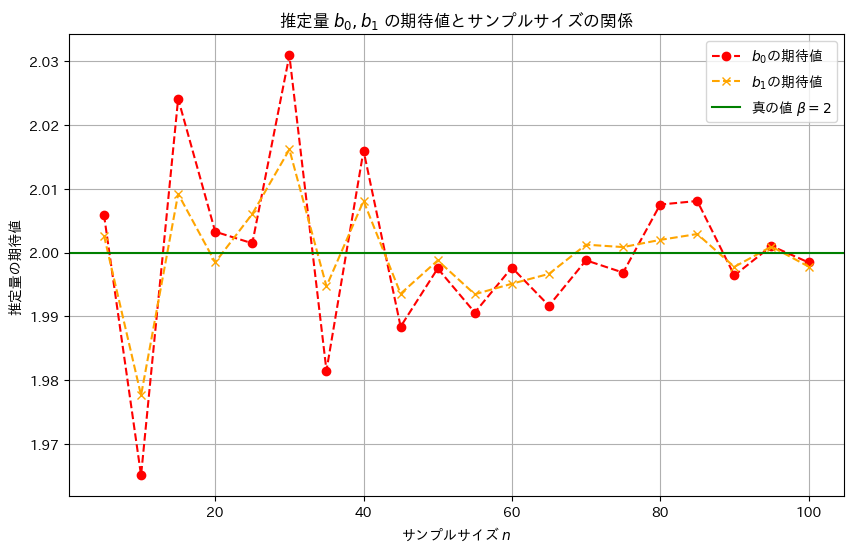
サンプルサイズnが大きくなるほど、推定量b0,b1は真の値βに近づくことが確認できました。また、b1の分散はb0の分散より小さく見え、b1はb0より安定した推定量のようです。
次に、推定量b0,b1の分布を確認してみます。それぞれのヒストグラムを重ねて表示してみます。
# 2016 Q3(1) 2024.11.20
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 100 # サンプルサイズ
true_beta = 2 # 真のβ
sigma = 1 # 誤差の標準偏差
simulations = 10000 # シミュレーション回数
b0_samples = []
b1_samples = []
# シミュレーションを実施
for _ in range(simulations):
xi = np.random.uniform(1, 10, n)
epsilon_i = np.random.normal(0, sigma, n)
Yi = true_beta * xi + epsilon_i
b0_samples.append(np.mean(Yi / xi))
b1_samples.append(np.sum(Yi) / np.sum(xi))
# b0 と b1 の分布を重ねてプロット
plt.figure(figsize=(10, 6))
plt.hist(b0_samples, bins=30, density=True, color='red', alpha=0.5, label='$b_0$')
plt.hist(b1_samples, bins=30, density=True, color='orange', alpha=0.5, label='$b_1$')
plt.axvline(x=true_beta, color='green', linestyle='dashed', label='真の値 $\\beta=2$')
plt.title('$b_0$ と $b_1$ の分布 (n=100)')
plt.xlabel('推定値')
plt.ylabel('頻度')
plt.legend()
plt.grid(True)
plt.show()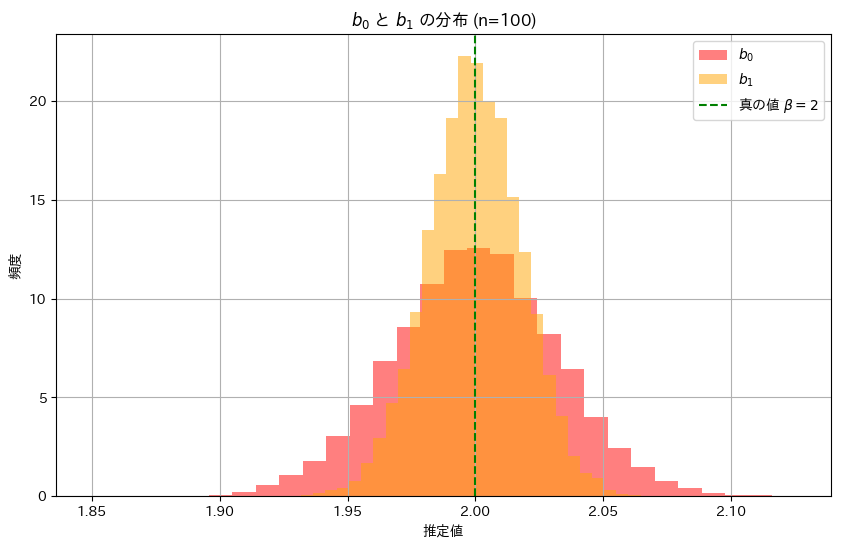
推定量b1の分布は、推定量b0の分布に比べて幅が狭く、b1の分散のほうがb0よりも小さく、安定した推定であることが分かりました。