ホーム » 尤度比
「尤度比」カテゴリーアーカイブ
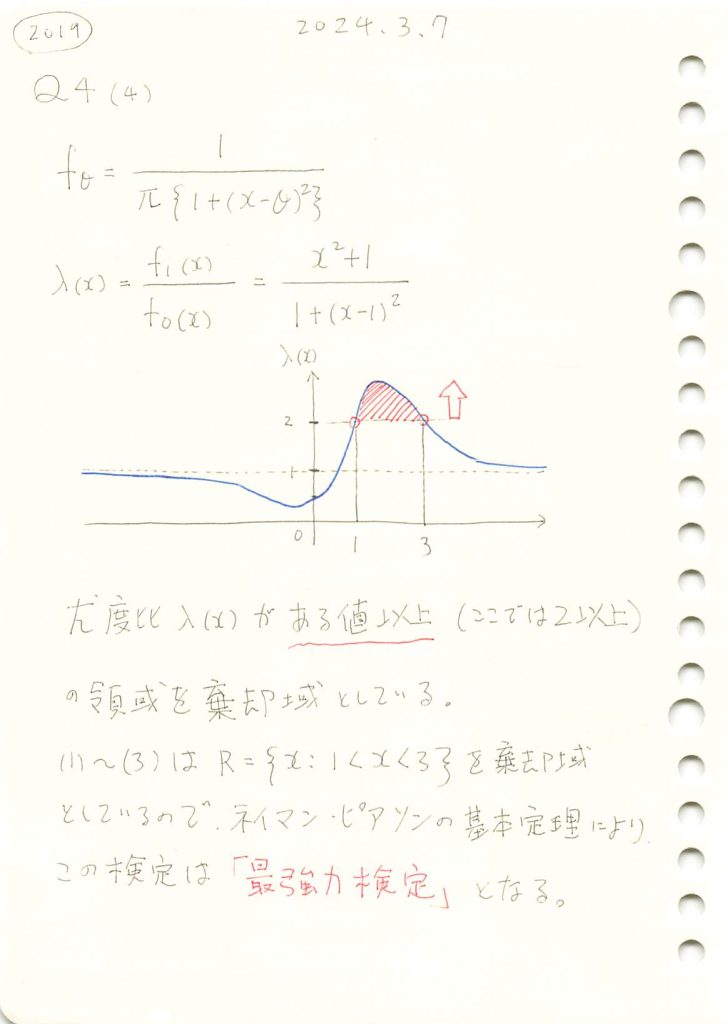
2019 Q4(4)
コーシー分布の検定で、与えられた棄却域が最強力検定になることを示しました。
コード
棄却域をR={x:1<x<3}にする検定が最強力検定になるのか確認するために、尤度比λ(x)のグラフを描画します。
# 2019 Q4(4) 2024.9.26
import numpy as np
import matplotlib.pyplot as plt
# 尤度比 λ(x) の計算
def likelihood_ratio(x):
return (1 + x**2) / (1 + (x - 1)**2)
# x の範囲を設定
x_values = np.linspace(-5, 5, 500)
# λ(x) の値を計算
lambda_values = likelihood_ratio(x_values)
# グラフを描画
plt.figure(figsize=(10, 6))
plt.plot(x_values, lambda_values, label=r'尤度比 $\lambda(x) = \frac{1 + x^2}{1 + (x - 1)^2}$', color='b')
# 棄却域 1 < x < 3 を塗りつぶす（透明度を追加）
plt.axvspan(1, 3, color='yellow', alpha=0.3, label=r'棄却域 $1 < x < 3$')
# λ(x) >= 2 の部分を赤で塗る
plt.fill_between(x_values, lambda_values, 2, where=(lambda_values >= 2), color='red', alpha=0.3, label=r'$\lambda(x) \geq 2$')
# グラフの装飾
plt.axhline(2, color='green', linestyle='--', label=r'閾値 $\lambda(x) = 2$')
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title(r'尤度比 $\lambda(x)$ と棄却域 $1 < x < 3$, $\lambda(x) \geq 2$ の範囲')
plt.xlabel('x')
plt.ylabel(r'$\lambda(x)$')
plt.grid(True)
plt.legend()
# グラフを表示
plt.show()
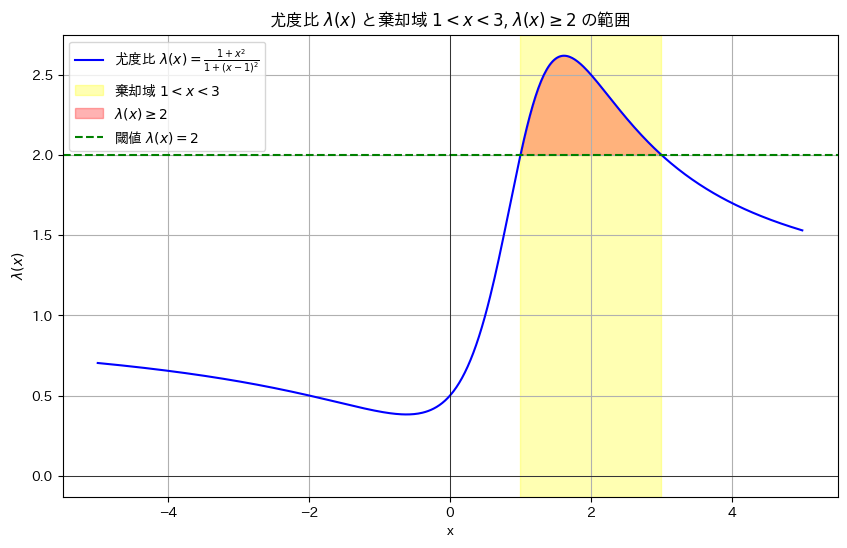
棄却域は尤度比λ(x)>c (ここではc=2)で定義できるので、これは最強力検定と言えます。
ところでx->-∞で尤度比λ(x)はどこに収束するのでしょうか。
import numpy as np
import matplotlib.pyplot as plt
# 尤度比 λ(x) の計算
def likelihood_ratio(x):
return (1 + x**2) / (1 + (x - 1)**2)
# x の範囲を設定（左側を広げる）
x_values = np.linspace(-50, 5, 500)
# λ(x) の値を計算
lambda_values = likelihood_ratio(x_values)
# グラフを描画
plt.figure(figsize=(10, 6))
plt.plot(x_values, lambda_values, label=r'尤度比 $\lambda(x) = \frac{1 + x^2}{1 + (x - 1)^2}$', color='b')
# 閾値を視覚化
plt.axhline(1, color='purple', linestyle='--', label=r'極限 $\lambda(x) \to 1$ as $x \to -\infty$')
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title(r'尤度比 $\lambda(x)$ の概形 ($x \to -\infty$ の範囲)')
plt.xlabel('x')
plt.ylabel(r'$\lambda(x)$')
plt.grid(True)
plt.legend()
# グラフを表示
plt.show()
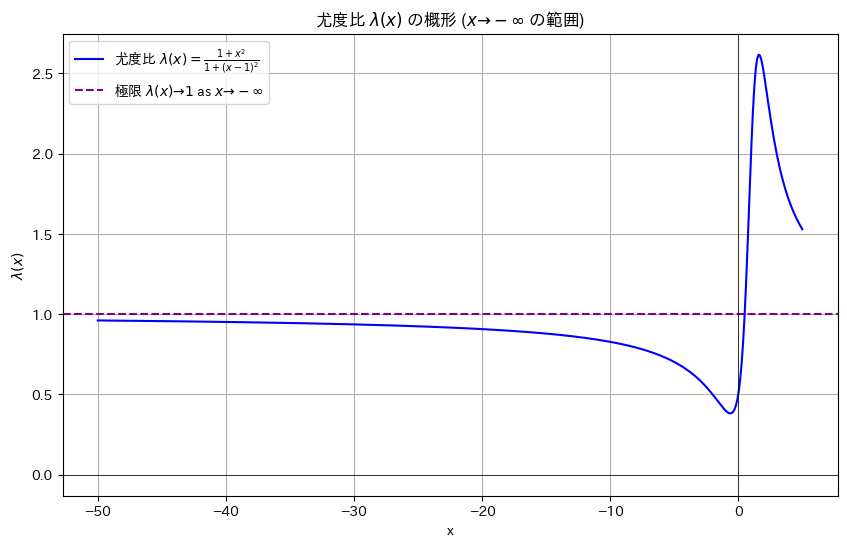
1.0に収束するようです。
よって、cは1以上で、且つ尤度比λ(x)が最大となるx = 1.61803398874989(黄金比)が棄却域に含まれていれば最強力検定になります。
2019 Q4(3)
コーシー分布のパラメータ違いの尤度比の概形を描きました。
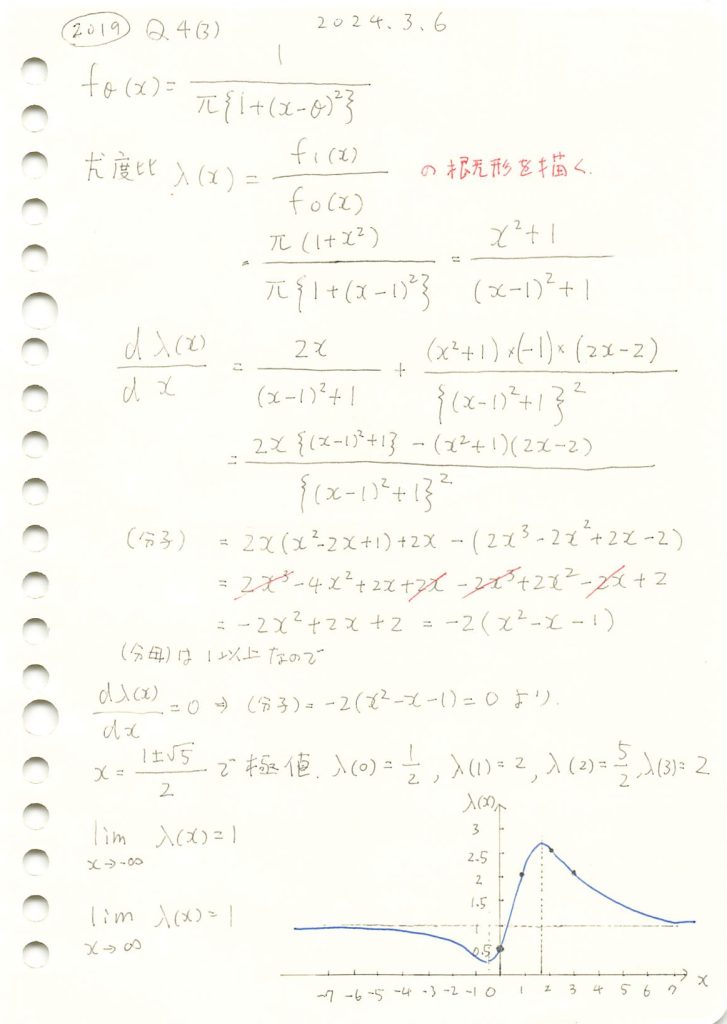
コード
尤度比λ(x)のグラフを描画します。
# 2019 Q4(3) 2024.9.25
import numpy as np
import matplotlib.pyplot as plt
# 尤度比 λ(x) の計算
def likelihood_ratio(x):
return (1 + x**2) / (1 + (x - 1)**2)
# x の範囲を設定
x_values = np.linspace(-5, 5, 500)
# λ(x) の値を計算
lambda_values = likelihood_ratio(x_values)
# グラフを描画
plt.figure(figsize=(10, 6))
plt.plot(x_values, lambda_values, label=r'尤度比 $\lambda(x) = \frac{1 + x^2}{1 + (x - 1)^2}$', color='b')
plt.scatter([1, 3], [2, 2], color='red', zorder=5) # x = 1 および x = 3 の点をプロット
# グラフの装飾
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title(r'尤度比 $\lambda(x)$ の概形')
plt.xlabel('x')
plt.ylabel(r'$\lambda(x)$')
plt.grid(True)
plt.legend()
# グラフを表示
plt.show()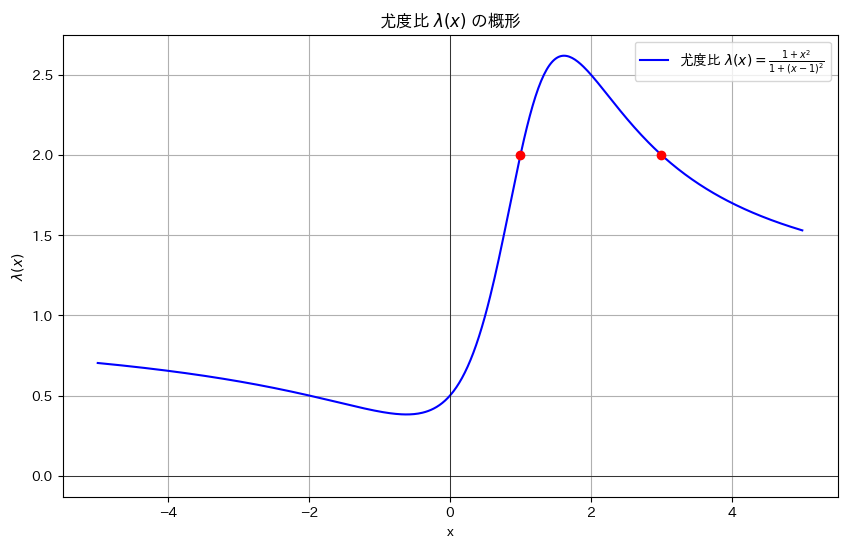
谷と山を持つ形状をしています。
次に、尤度関数λ(x)の1次導関数と2次導関数から、極値と形状(山か谷か)を導きます。
# 2019 Q4(3) 2024.9.25
import sympy as sp
from IPython.display import display
# 尤度比 λ(x) の式を定義
x = sp.symbols('x')
lambda_x = (1 + x**2) / (1 + (x - 1)**2)
# 1次導関数を計算
lambda_prime = sp.diff(lambda_x, x)
print("1次導関数 λ'(x):")
display(lambda_prime)
print()
# 1次導関数が0となる点（極値候補）を解く
critical_points = sp.solve(lambda_prime, x)
print("極値候補:")
display(critical_points)
print()
# 2次導関数を計算して極値の性質を確認
lambda_double_prime = sp.diff(lambda_prime, x)
print("2次導関数 λ''(x):")
display(lambda_double_prime)
print()
# 各極値候補の 2次導関数の値を調べる
for point in critical_points:
second_derivative_value = lambda_double_prime.subs(x, point)
# 極値の場所を数値評価する
point_value = point.evalf()
# 2次導関数の値も数値評価する
second_derivative_value_numeric = second_derivative_value.evalf()
if second_derivative_value > 0:
print(f"x = {point} で谷（極小値） (数値: {point_value})")
print(f"2次導関数の値: {second_derivative_value_numeric}")
elif second_derivative_value < 0:
print(f"x = {point} で山（極大値） (数値: {point_value})")
print(f"2次導関数の値: {second_derivative_value_numeric}")
else:
print(f"x = {point} で特異点か平坦な極値 (数値: {point_value})")
print(f"2次導関数の値: {second_derivative_value_numeric}")
以上のように求まりました。