ホーム » 尖度
「尖度」カテゴリーアーカイブ
2017 Q1(4)
サンプル数が十分に大きい時のサンプル平均の歪度と尖度がどのようになるか考察した。

コード
Xの標本平均の歪度と尖度(過剰尖度)はサンプルサイズnが十分大きいときにどう変化するのか確認します。
# 2017 Q1(4) 2024.10.27
from scipy.stats import skew, kurtosis, gamma
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータの設定
#np.random.seed(42) # 再現性のためのシード
num_simulations = 300000 # シミュレーションの繰り返し回数
sample_sizes = range(10, 1100, 50) # サンプルサイズを広げて設定
# 歪度と尖度を持つ母集団分布としてガンマ分布を使用(shape=2で正の歪度と尖度を持つ)
shape_param = 2.0 # ガンマ分布のshapeパラメータ
scale_param = 2.0 # ガンマ分布のscaleパラメータ
population_dist = gamma(a=shape_param, scale=scale_param)
# シミュレーション結果を保存するリスト
sample_mean_skewness = []
sample_mean_kurtosis = []
# 各サンプルサイズでのシミュレーションの実行
for n in sample_sizes:
skew_values = []
kurt_values = []
# シミュレーションを繰り返し
for _ in range(num_simulations):
sample = population_dist.rvs(size=n) # サンプルを抽出
sample_mean = np.mean(sample) # 標本平均
# 標本平均をリストに保存
skew_values.append(sample_mean)
kurt_values.append(sample_mean)
# 標本平均の歪度と尖度を計算
skewness_of_sample_mean = skew(skew_values)
kurtosis_of_sample_mean = kurtosis(kurt_values, fisher=False) - 3 # 過剰尖度に変換
# 結果を保存
sample_mean_skewness.append(skewness_of_sample_mean)
sample_mean_kurtosis.append(kurtosis_of_sample_mean)
# グラフの作成
plt.figure(figsize=(12, 6))
# 歪度のプロット
plt.subplot(1, 2, 1)
plt.plot(sample_sizes, sample_mean_skewness, marker='o', label='歪度')
plt.axhline(y=0, color='r', linestyle='--', label='理論値: 0')
plt.title('サンプルサイズと歪度の関係')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('歪度 ($\\bar{X}$)')
plt.legend()
plt.grid(True)
# 尖度のプロット
plt.subplot(1, 2, 2)
plt.plot(sample_sizes, sample_mean_kurtosis, marker='o', label='尖度(過剰尖度)')
plt.axhline(y=0, color='r', linestyle='--', label='理論値: 0')
plt.title('サンプルサイズと尖度の関係')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('尖度 ($\\bar{X}$)')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()
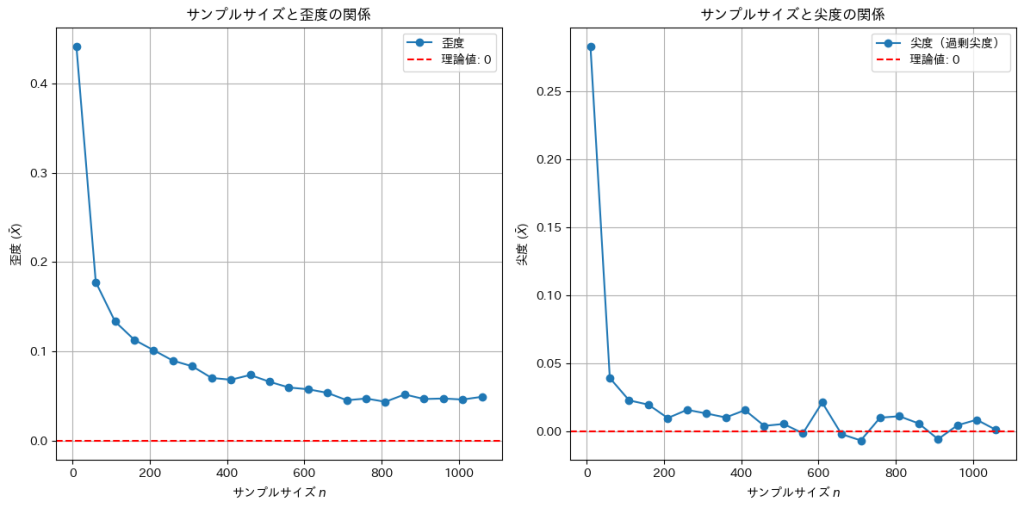
Xの標本平均の尖度(過剰尖度)はサンプルサイズnが大きくなると0に近づくことが確認できました。しかし歪度は0に近づくスピードは遅いです。Xが従うガンマ分布は元々歪度を持つ非対称な分布なので、そのようになります。サンプルサイズnを10,000まで大きくしてみます。
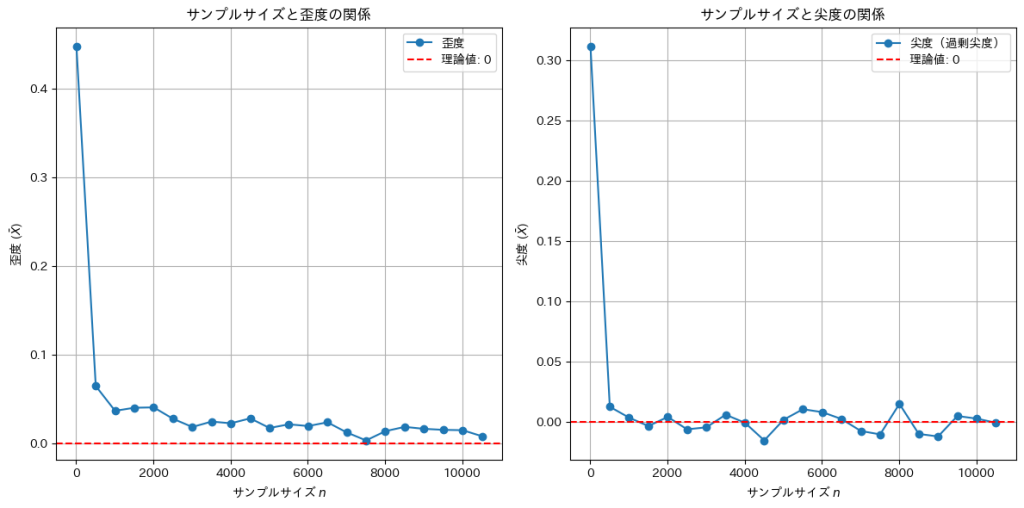
nが十分に大きくなったので歪度も0に近づきました。
次に、サンプルサイズnに伴う標本平均の分布が正規分布に近づく様子を確認します。
# 2017 Q1(4) 2024.10.27
import seaborn as sns
from scipy.stats import norm
# サンプルサイズの設定
selected_sample_sizes = [5, 20, 100, 200] # 表示するサンプルサイズの選択
num_simulations = 10000 # シミュレーションの繰り返し回数
# グラフの作成
plt.figure(figsize=(14, 10))
# 各サンプルサイズでのシミュレーションとヒストグラムの描画
for idx, n in enumerate(selected_sample_sizes):
sample_means = []
# シミュレーションの実行
for _ in range(num_simulations):
sample = population_dist.rvs(size=n) # サンプルを抽出
sample_mean = np.mean(sample) # 標本平均を計算
sample_means.append(sample_mean)
# ヒストグラムのプロット
plt.subplot(2, 2, idx + 1)
sns.histplot(sample_means, bins=30, kde=True, stat="density", color='blue', label='標本平均の分布')
# 正規分布のプロット
mean_of_means = np.mean(sample_means)
std_of_means = np.std(sample_means)
x = np.linspace(min(sample_means), max(sample_means), 100)
plt.plot(x, norm.pdf(x, mean_of_means, std_of_means), 'r--', label='正規分布')
# グラフの設定
plt.title(f'サンプルサイズ {n} の標本平均の分布')
plt.xlabel('標本平均')
plt.ylabel('密度')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()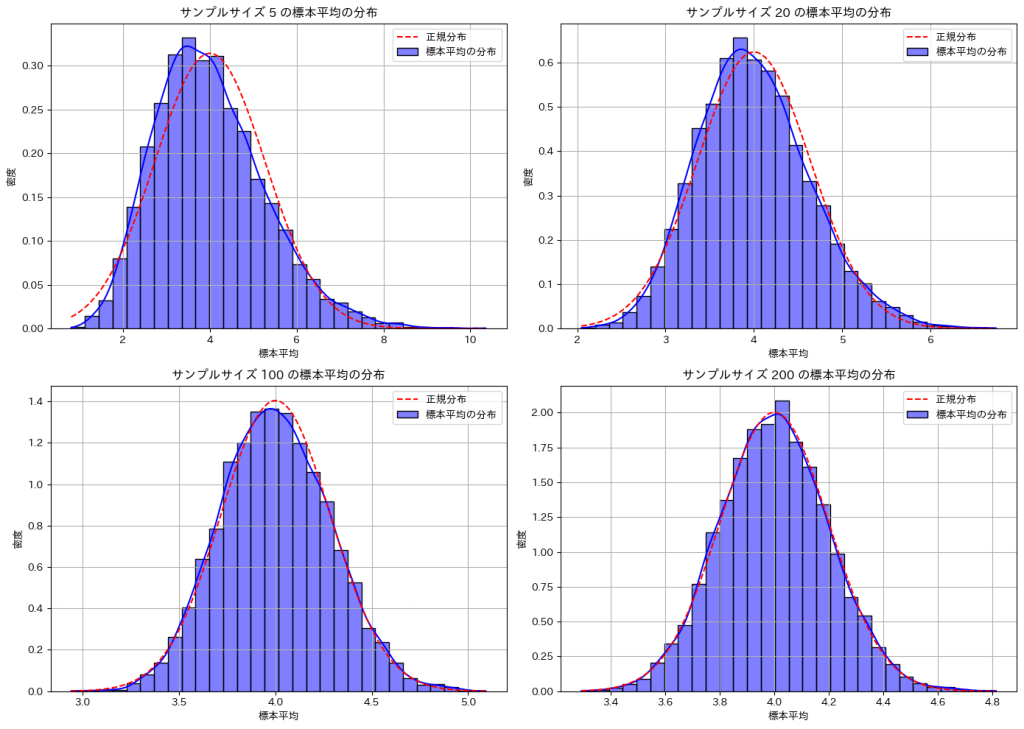
サンプルサイズnが大きくなるほど標本平均の分布は正規分布に近づくことが確認できました。
2017 Q1(3)
この前と同じ問ですが、解き方が間違っていたので、再チャレンジです。
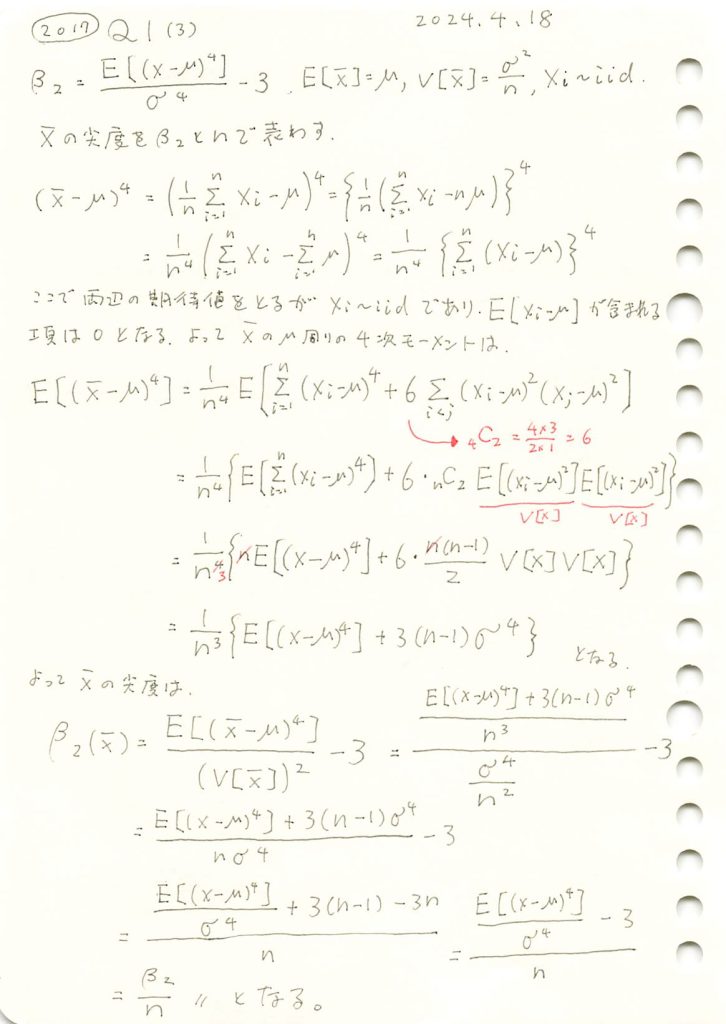
コード
Xの標本平均の尖度(過剰尖度)が![]() になるか確認するためにシミュレーションを行います。母集団分布はガンマ分布とします。比較のためシミュレーション回数は前問(歪度)と同じ回数とする。
になるか確認するためにシミュレーションを行います。母集団分布はガンマ分布とします。比較のためシミュレーション回数は前問(歪度)と同じ回数とする。
# 2017 Q1(3) 2024.10.26
from scipy.stats import kurtosis, gamma
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータの設定
num_simulations = 30000 # シミュレーションの繰り返し回数
sample_sizes = range(10, 110, 10) # サンプルサイズの設定
# 尖度を持つ母集団分布としてガンマ分布を使用(shape=2で正の尖度を持つ)
shape_param = 2.0 # ガンマ分布のshapeパラメータ
scale_param = 2.0 # ガンマ分布のscaleパラメータ
population_dist = gamma(a=shape_param, scale=scale_param)
# 理論的な過剰尖度(ガンマ分布の尖度の計算)
beta_2_theoretical = 6 / shape_param # ガンマ分布の過剰尖度
# シミュレーション結果を保存するリスト
sample_mean_excess_kurtosis = []
# 各サンプルサイズでのシミュレーションの実行
for n in sample_sizes:
kurt_values = []
# シミュレーションを繰り返し
for _ in range(num_simulations):
sample = population_dist.rvs(size=n) # サンプルを抽出
sample_mean = np.mean(sample) # 標本平均
kurt_values.append(sample_mean)
# 標本平均の尖度を計算し、過剰尖度に変換(-3)
kurtosis_of_sample_mean = kurtosis(kurt_values, fisher=False) - 3 # 尖度を計算し、過剰尖度に変換
sample_mean_excess_kurtosis.append(kurtosis_of_sample_mean)
# 理論値の計算
theoretical_excess_kurtosis = [beta_2_theoretical / n for n in sample_sizes]
# グラフの作成
plt.figure(figsize=(10, 6))
# シミュレーション結果のプロット
plt.plot(sample_sizes, sample_mean_excess_kurtosis, marker='o', label='シミュレーション結果 (過剰尖度)')
plt.plot(sample_sizes, theoretical_excess_kurtosis, color='r', linestyle='--', label='理論値: $\\frac{\\beta_2}{n}$')
plt.title('$\\bar{X}$ の過剰尖度のシミュレーションと理論値の比較')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$\\bar{X}$ の過剰尖度')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()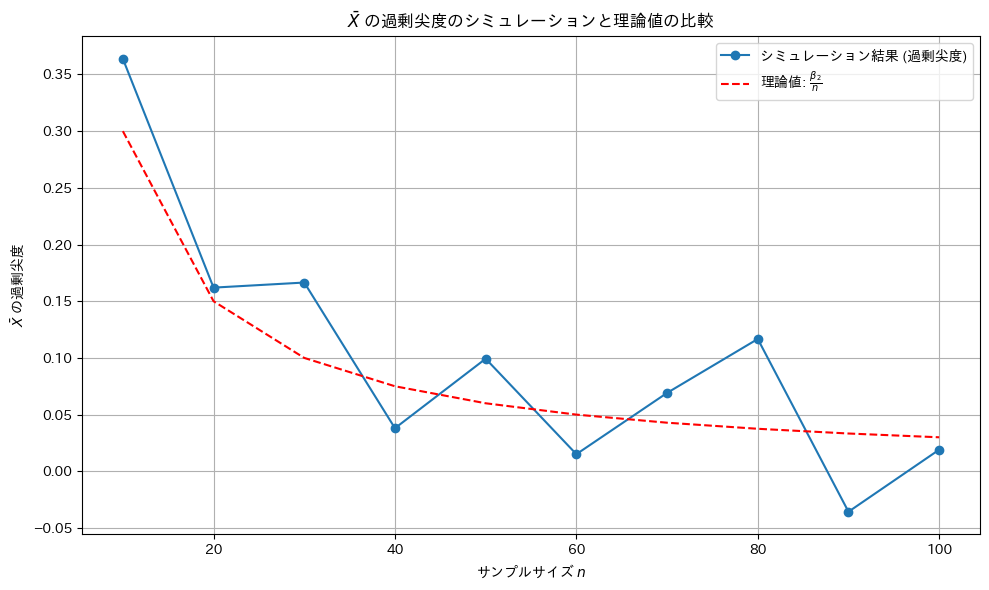
尖度は理論値に沿うものの、歪度(前問)より更に外れ値の影響を受けやすいため分散が大きい。
シミュレーション回数を10倍にしてみます。
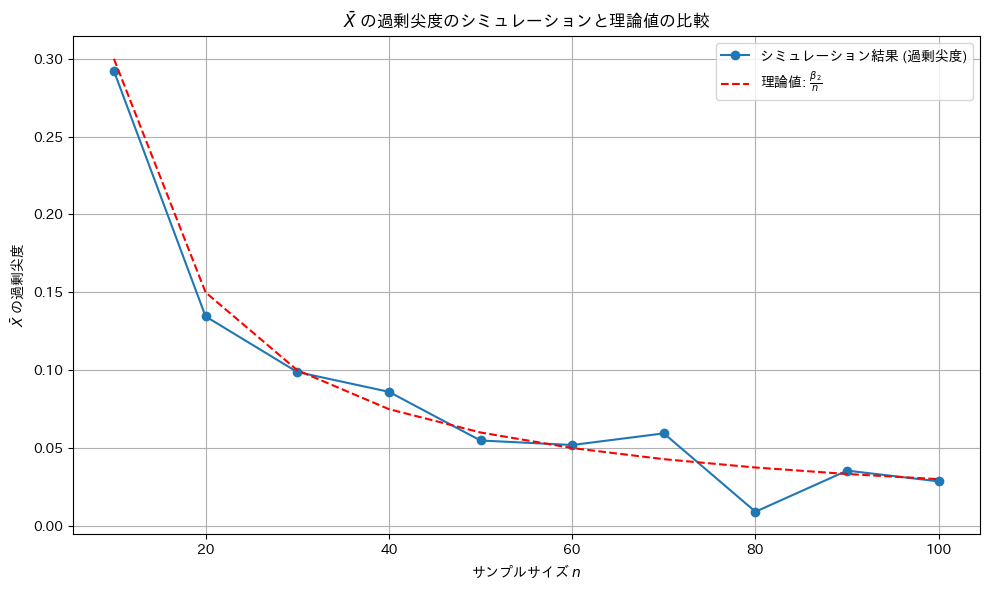
尖度は理論値に近づきました。