ホーム » 仮説検定
「仮説検定」カテゴリーアーカイブ
2014 Q3(1)
液体のサンプルの体積と重さから比重がβ0であるという検定を体積と重さの分散が既知の場合と未知の場合でそれぞれ方式を求めました。

コード
帰無仮説![]() の下で、真の値
の下で、真の値![]() が仮説と一致する場合(
が仮説と一致する場合(![]() )と異なる場合(
)と異なる場合(![]() )におけるZ検定とT検定の棄却率を比較します。
)におけるZ検定とT検定の棄却率を比較します。
# 2014 Q3(1) 2025.1.5 (2025.1.6修正)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, t
# Parameters
n = 30 # サンプルサイズ
beta_0 = 1.2 # 仮説のβ
sigma_X = 1.0 # Xの標準偏差
sigma_Y = 3.0 # Yの標準偏差
mu_X = 5.0 # Xの平均 (十分大きく設定)
alpha = 0.05 # 有意水準
num_simulations = 1000 # シミュレーション回数
# 分散の妥当性を確認
beta_true_values = [1.2, 1.5] # 真のβの候補
# 結果を格納するリスト
simulated_Z_dict = {}
simulated_T_dict = {}
rejection_rates_Z = {}
rejection_rates_T = {}
for beta_true in beta_true_values:
if sigma_Y**2 <= (beta_true * sigma_X)**2:
raise ValueError(f"sigma_Y^2は(beta_true * sigma_X)^2より大きくなければなりません (beta_true={beta_true})。")
# 誤差項の分散を計算
sigma_epsilon_squared = sigma_Y**2 + (beta_true * sigma_X)**2
# Z統計量とT統計量を格納するリスト
simulated_Z = []
simulated_T = []
reject_count_Z = 0
reject_count_T = 0
for _ in range(num_simulations):
# Xを正規分布で生成
X = np.random.normal(mu_X, sigma_X, n) # 平均mu_X、標準偏差sigma_X
epsilon = np.random.normal(0, np.sqrt(sigma_epsilon_squared), n) # 誤差項
# Yを生成
Y = beta_true * X + epsilon
# Z検定 (分散既知)
X_bar = np.mean(X)
Y_bar = np.mean(Y)
Z = (Y_bar - beta_0 * X_bar) / np.sqrt((sigma_Y**2 + beta_0**2 * sigma_X**2) / n)
simulated_Z.append(Z)
if abs(Z) > norm.ppf(1 - alpha / 2): # 両側検定
reject_count_Z += 1
# T検定 (分散未知)
U = Y - beta_0 * X
U_bar = np.mean(U)
S_square = np.sum((U - U_bar)**2) / (n - 1)
T = (Y_bar - beta_0 * X_bar) / np.sqrt(S_square / n)
simulated_T.append(T)
if abs(T) > t.ppf(1 - alpha / 2, df=n - 1): # 両側検定
reject_count_T += 1
simulated_Z_dict[beta_true] = simulated_Z
simulated_T_dict[beta_true] = simulated_T
rejection_rates_Z[beta_true] = reject_count_Z / num_simulations
rejection_rates_T[beta_true] = reject_count_T / num_simulations
# 棄却率を表示
print("検定条件: H0: β = 1.2")
for beta_true in beta_true_values:
print(f"真のβ = {beta_true}: Z検定の棄却率 = {rejection_rates_Z[beta_true]:.4f}, T検定の棄却率 = {rejection_rates_T[beta_true]:.4f}")
# グラフ用の範囲を定義
x_values = np.linspace(-4, 4, 1000)
# 理論的なZ分布 (帰無仮説H0: beta = beta_0)
z_pdf = norm.pdf(x_values, 0, 1)
# Z分布のプロット
plt.figure(figsize=(12, 6))
plt.plot(x_values, z_pdf, label="理論分布 (H0: 標準正規分布)", color='blue')
for beta_true, simulated_Z in simulated_Z_dict.items():
plt.hist(simulated_Z, bins=30, density=True, alpha=0.6, label=f"シミュレーション (真のβ = {beta_true})")
plt.axvline(x=norm.ppf(1 - alpha / 2), color='red', linestyle='dashed', label=f"有意水準の境界 (+{norm.ppf(1 - alpha / 2):.2f})")
plt.axvline(x=-norm.ppf(1 - alpha / 2), color='red', linestyle='dashed', label=f"有意水準の境界 (-{norm.ppf(1 - alpha / 2):.2f})")
plt.title("Z分布: 理論分布とシミュレーションの比較 (真のβの変化)", fontsize=16)
plt.xlabel("Z値", fontsize=12)
plt.ylabel("密度", fontsize=12)
plt.legend()
plt.grid()
plt.show()
# 理論的なT分布 (帰無仮説H0: beta = beta_0)
t_pdf = t.pdf(x_values, df=n - 1)
# T分布のプロット
plt.figure(figsize=(12, 6))
plt.plot(x_values, t_pdf, label=f"理論分布 (H0: t分布, 自由度={n - 1})", color='blue')
for beta_true, simulated_T in simulated_T_dict.items():
plt.hist(simulated_T, bins=30, density=True, alpha=0.6, label=f"シミュレーション (真のβ = {beta_true})")
plt.axvline(x=t.ppf(1 - alpha / 2, df=n - 1), color='red', linestyle='dashed', label=f"有意水準の境界 (+{t.ppf(1 - alpha / 2, df=n - 1):.2f})")
plt.axvline(x=-t.ppf(1 - alpha / 2, df=n - 1), color='red', linestyle='dashed', label=f"有意水準の境界 (-{t.ppf(1 - alpha / 2, df=n - 1):.2f})")
plt.title("T分布: 理論分布とシミュレーションの比較 (真のβの変化)", fontsize=16)
plt.xlabel("T値", fontsize=12)
plt.ylabel("密度", fontsize=12)
plt.legend()
plt.grid()
plt.show()検定条件: H0: β = 1.2
真のβ = 1.2: Z検定の棄却率 = 0.0390, T検定の棄却率 = 0.0400
真のβ = 1.5: Z検定の棄却率 = 0.7080, T検定の棄却率 = 0.6490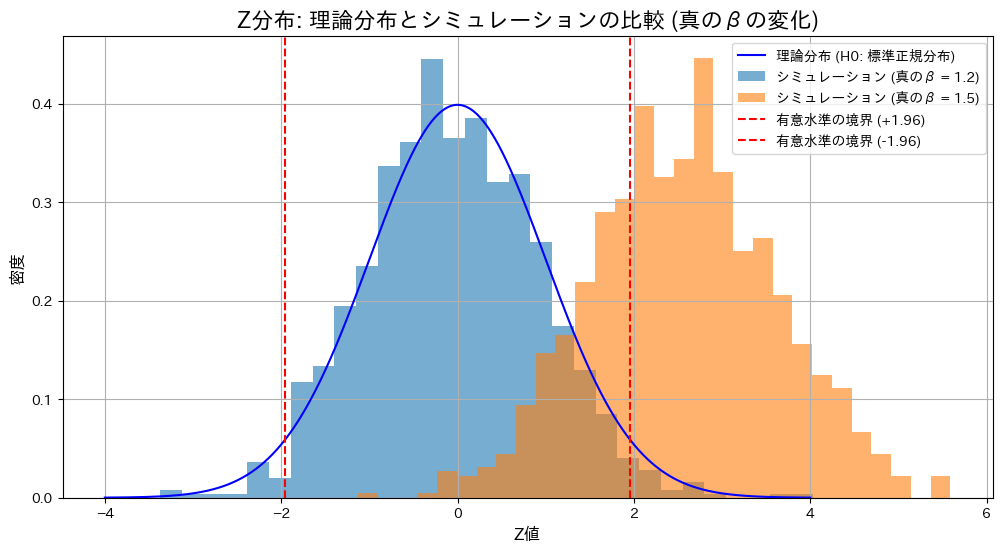
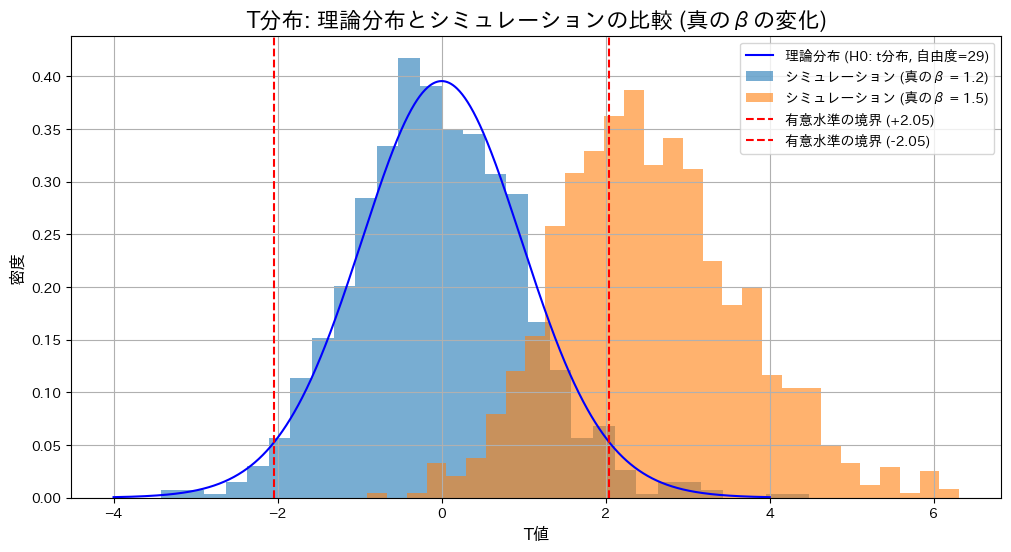
帰無仮説が正しい場合(![]() )、Z検定とT検定の棄却率は有意水準付近で期待通りの結果を示しました。一方、真の値が異なる場合(
)、Z検定とT検定の棄却率は有意水準付近で期待通りの結果を示しました。一方、真の値が異なる場合(![]() )、両検定で棄却域が大幅に上昇し、帰無仮説を適切に棄却できていることが確認されました。また、真の値が異なる場合には、Z検定の棄却率がT検定をわずかに上回る結果となりました。これは、分散既知の場合のZ検定が分散未知のT検定に比べて統計量の推定が安定しているためと考えられます。
)、両検定で棄却域が大幅に上昇し、帰無仮説を適切に棄却できていることが確認されました。また、真の値が異なる場合には、Z検定の棄却率がT検定をわずかに上回る結果となりました。これは、分散既知の場合のZ検定が分散未知のT検定に比べて統計量の推定が安定しているためと考えられます。
2015 Q4(3)
確率の分割表に対称性があるという仮説の下での尤度比検定を行いp値が0.01より小さいか判定しました。

コード
![]() が成り立つかを確認するために、尤度比検定量
が成り立つかを確認するために、尤度比検定量![]() を求め、尤度比検定を行います。
を求め、尤度比検定を行います。
# 2015 Q4(3) 2024.12.19
import numpy as np
from scipy.stats import chi2
# 観測度数表
observed_counts = np.array([[1520, 266, 124, 66],
[234, 1512, 432, 78],
[117, 362, 1772, 205],
[36, 82, 179, 492]])
I = observed_counts.shape[0] # 行・列のサイズ
# 尤度比統計量 G^2 の計算 (対角要素を除外)
G2 = 2 * sum(
observed_counts[i, j] * np.log(2 * observed_counts[i, j] / (observed_counts[i, j] + observed_counts[j, i]))
for i in range(I) for j in range(I) if i != j
)
# 自由度の計算 (非対角要素の数: I(I-1)/2)
df = (I * (I - 1)) // 2
# P値の計算
p_value = 1 - chi2.cdf(G2, df)
# 結果の表示
print(f"尤度比統計量 G^2: {G2:.4f}")
print(f"自由度: {df}")
print(f"P値: {p_value:.10f}")
# 帰無仮説の判定
if p_value < 0.01:
print("P値は0.01より小さいため、帰無仮説 H_0 は棄却されます。")
else:
print("P値は0.01以上のため、帰無仮説 H_0 は棄却されません。")
尤度比統計量 G^2: 19.2492
自由度: 6
P値: 0.0037628518
P値は0.01より小さいため、帰無仮説 H_0 は棄却されます。P値は0.01より小さいため、帰無仮説 ![]() は棄却されました。
は棄却されました。
2015 Q2(4)
標本平均の片側検定での検出力を特定の値以上にするために必要なサンプル数を求めました。
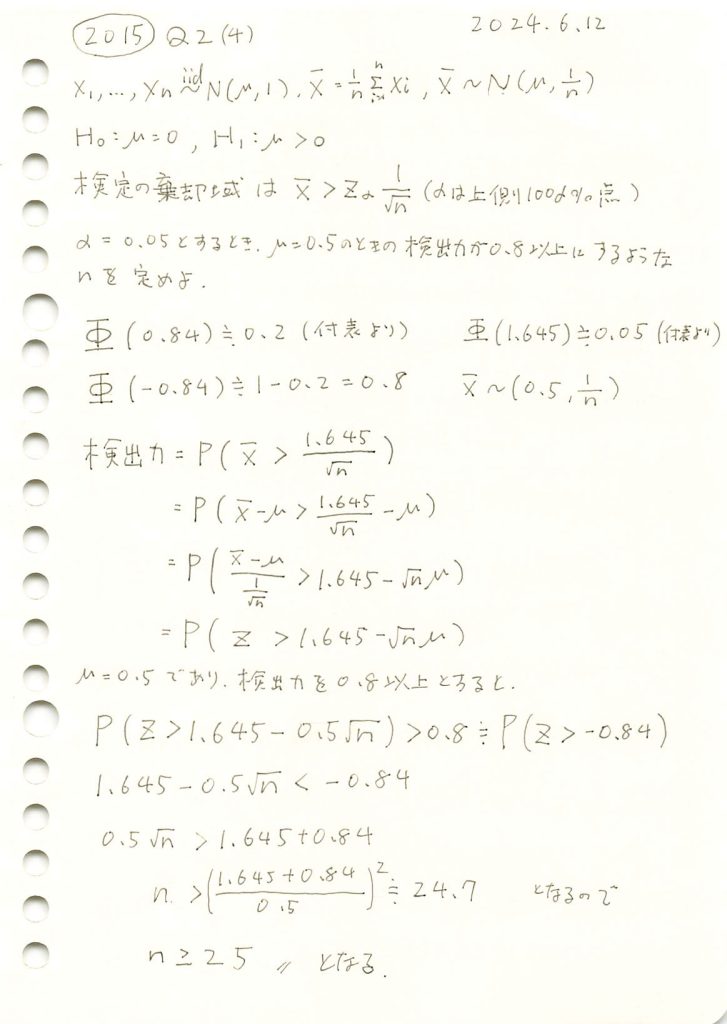
コード
有意水準α=0.05において、標本サイズnと検出力の関係を理論値とシミュレーションで比較し、目標の検出力0.8を達成するために必要な標本サイズnを調べます。
# 2015 Q2(4) 2024.12.10
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 設定
alpha = 0.05 # 有意水準
target_power = 0.8 # 目標検出力
mu = 0.5 # 真の平均
z_alpha = norm.ppf(1 - alpha) # 臨界値 z_alpha
z_power = norm.ppf(target_power) # 検出力に対応する Z 値
# 理論的な検出力の計算
n_values = np.arange(1, 51, 1) # 標本の大きさ n = 1, 2, ..., 50
powers_theoretical = [1 - norm.cdf(z_alpha - mu * np.sqrt(n)) for n in n_values]
# 実際の検出力を乱数シミュレーションで計算
num_simulations = 10000 # シミュレーション回数
n_sim_values = np.arange(5, 51, 5) # n = 5, 10, ..., 50
powers_simulated = []
for n in n_sim_values:
# 標本平均を生成
samples = np.random.normal(mu, 1 / np.sqrt(n), num_simulations)
# 標本平均が臨界値を超えた割合を計算
rejection_rate = np.mean(samples > z_alpha / np.sqrt(n))
powers_simulated.append(rejection_rate)
# グラフの描画
plt.figure(figsize=(10, 6))
# 理論的な検出力の曲線
plt.plot(n_values, powers_theoretical, label="理論的な検出力 (Power)", color="blue")
# シミュレーションによる検出力
plt.scatter(n_sim_values, powers_simulated, color="red", label="シミュレーションによる検出力", zorder=5)
# 検出力の目標ラインと必要な標本サイズライン
plt.axhline(y=target_power, color="red", linestyle="--", label=f"目標検出力 Power = {target_power}")
plt.axvline(x=25, color="green", linestyle="--", label="必要な標本数 n = 25")
# グラフの設定
plt.xlabel("標本の大きさ $n$", fontsize=12)
plt.ylabel("検出力 (Power)", fontsize=12)
plt.title("理論値とシミュレーションによる検出力の比較", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()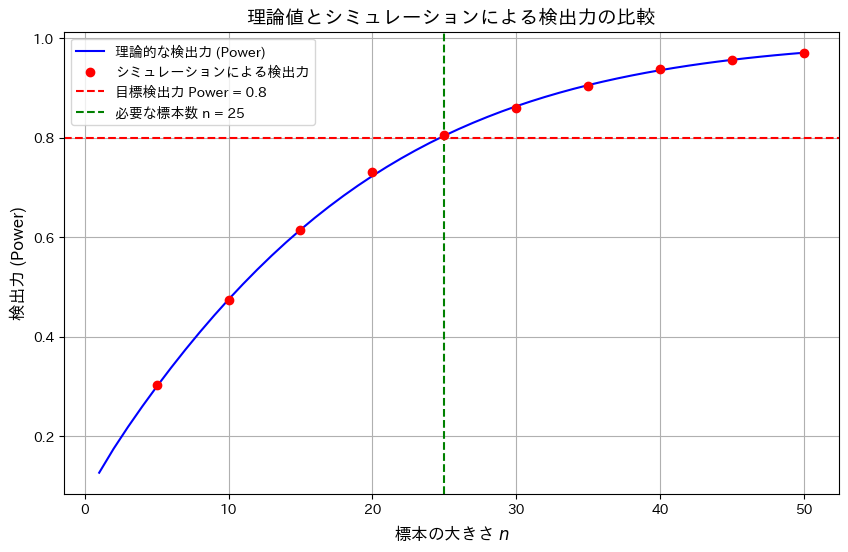
標本サイズnの増加が検出力の向上に寄与することを確認しました。また理論とシミュレーション結果が一致し、目標の検出力0.8を達成するためにはn=25が必要であることが確認できました。
2015 Q2(3)
標本平均の片側検定での検出力を求め、母平均と検出力の関係を描きました。

コード
有意水準 α=0.05、サンプルサイズ n=9およびn=16の場合における検出力を真の平均 μを変化させて視覚化します。また、μ=0.4,0.8での検出力を計算します。
# 2015 Q2(3) 2024.12.9
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 定義
alpha = 0.05 # 有意水準
z_alpha = norm.ppf(1 - alpha) # 臨界値 z_alpha
sample_sizes = [9, 16] # n = 9, 16
true_means = [0.4, 0.8] # 真の平均 μ = 0.4, 0.8
# 検出力の計算関数
def compute_power(mu, n, z_alpha):
z_value = z_alpha - mu * np.sqrt(n)
power = 1 - norm.cdf(z_value)
return power
# 検出力を計算
mu_values = np.linspace(0, 1.5, 100) # 真の平均 μ の範囲
powers_n9 = [compute_power(mu, n=9, z_alpha=z_alpha) for mu in mu_values]
powers_n16 = [compute_power(mu, n=16, z_alpha=z_alpha) for mu in mu_values]
# 指定された μ = 0.4, 0.8 の検出力を計算
specific_powers = {
(n, mu): compute_power(mu, n, z_alpha)
for n in sample_sizes
for mu in true_means
}
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(mu_values, powers_n9, label="検出力 (n=9)", linestyle="--", color="blue")
plt.plot(mu_values, powers_n16, label="検出力 (n=16)", linestyle="-", color="green")
# μ = 0.4, 0.8 の場合の検出力をプロット
for (n, mu), power in specific_powers.items():
plt.scatter(mu, power, label=f"n={n}, μ={mu}, Power={power:.2f}", zorder=5)
# グラフの設定
plt.xlabel("真の平均 $\\mu$", fontsize=12)
plt.ylabel("検出力 (Power)", fontsize=12)
plt.title("検出力の挙動 ($n=9$ および $n=16$ の場合)", fontsize=14)
plt.axhline(y=alpha, color="red", linestyle=":", label=f"有意水準 α={alpha}")
plt.legend()
plt.grid(True)
plt.show()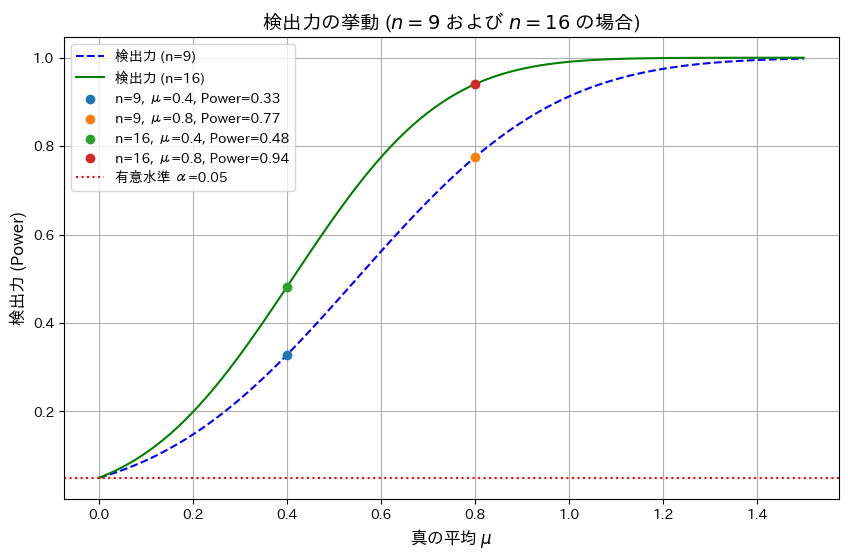
シミュレーションの結果、サンプルサイズnが増加することで検出力が向上することと、真の平均μが大きくなるほど検出力が1に近づくことが分かりました。
2015 Q2(2)
P値が有意水準より小さくなることと、観測値が棄却域より大きくなることが同等である事を示しました。

コード
標本平均![]() が棄却域に入る条件と、P値が有意水準 α以下となる条件が一致することをシミュレーションで確認します。
が棄却域に入る条件と、P値が有意水準 α以下となる条件が一致することをシミュレーションで確認します。
# 2015 Q2(2) 2024.12.8
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# シミュレーション設定
n = 10 # 標本サイズ
mu_0 = 0 # 帰無仮説の平均
sigma = 1 # 標準偏差
alpha = 0.05 # 有意水準
num_simulations = 10000 # シミュレーション回数
# z_alpha (有意水準に対応する臨界値)
z_alpha = norm.ppf(1 - alpha)
threshold = z_alpha / np.sqrt(n) # 棄却域の閾値
# シミュレーションで標本平均を生成
samples = np.random.normal(mu_0, sigma, (num_simulations, n))
x_bar = np.mean(samples, axis=1)
# 棄却域に入るかどうかを確認
in_rejection_region = x_bar > threshold
# P値の計算
p_values = 1 - norm.cdf(x_bar * np.sqrt(n) / sigma)
# P値が有意水準以下かどうかを確認
p_value_condition = p_values <= alpha
# 棄却域とP値の条件が一致する割合を計算
agreement_rate = np.mean(in_rejection_region == p_value_condition)
# 棄却域に落ちる割合とP値がα以下になる割合の比較
rejection_rate = np.mean(in_rejection_region)
p_value_rate = np.mean(p_value_condition)
# 結果の出力
print(f"シミュレーション回数: {num_simulations}")
print(f"有意水準 α: {alpha}")
print(f"棄却域条件とP値条件の一致率: {agreement_rate:.3f}")
print(f"棄却域に落ちる割合: {rejection_rate:.3f}")
print(f"P値がα以下になる割合: {p_value_rate:.3f}")
# グラフの描画
plt.figure(figsize=(12, 6))
# 標本平均 x̄ の分布
plt.hist(x_bar, bins=50, color="skyblue", alpha=0.7, edgecolor="black", label="標本平均 $\\bar{X}$ の分布")
plt.axvline(threshold, color="red", linestyle="--", label=f"棄却域の閾値 $z_{{\\alpha}}/\\sqrt{{n}} = {threshold:.3f}$")
plt.fill_betweenx([0, plt.gca().get_ylim()[1]], threshold, plt.gca().get_xlim()[1], color="red", alpha=0.2, label="棄却域")
plt.xlabel("標本平均 $\\bar{X}$", fontsize=12)
plt.ylabel("度数", fontsize=12)
plt.title("標本平均 $\\bar{X}$ の分布と棄却域", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()
# P値の分布
plt.figure(figsize=(12, 6))
plt.hist(p_values, bins=50, color="lightgreen", alpha=0.7, edgecolor="black", label="P値の分布")
plt.axvline(alpha, color="blue", linestyle="--", label=f"有意水準 $\\alpha = {alpha}$")
plt.fill_betweenx([0, plt.gca().get_ylim()[1]], 0, alpha, color="blue", alpha=0.2, label="P値が $\\leq \\alpha$ の領域")
plt.xlabel("P値", fontsize=12)
plt.ylabel("度数", fontsize=12)
plt.title("P値の分布と有意水準", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()
シミュレーション回数: 10000
有意水準 α: 0.05
棄却域条件とP値条件の一致率: 1.000
棄却域に落ちる割合: 0.052
P値がα以下になる割合: 0.052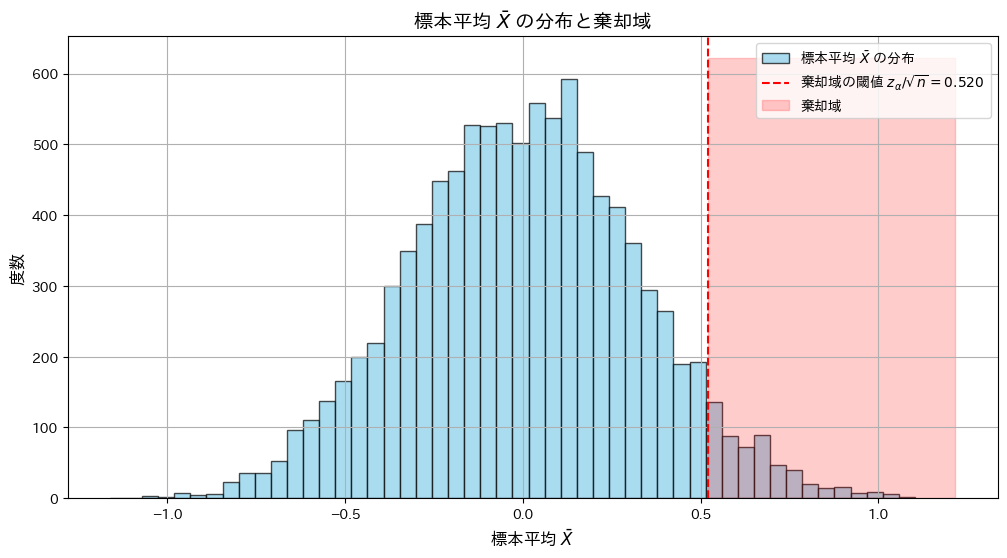
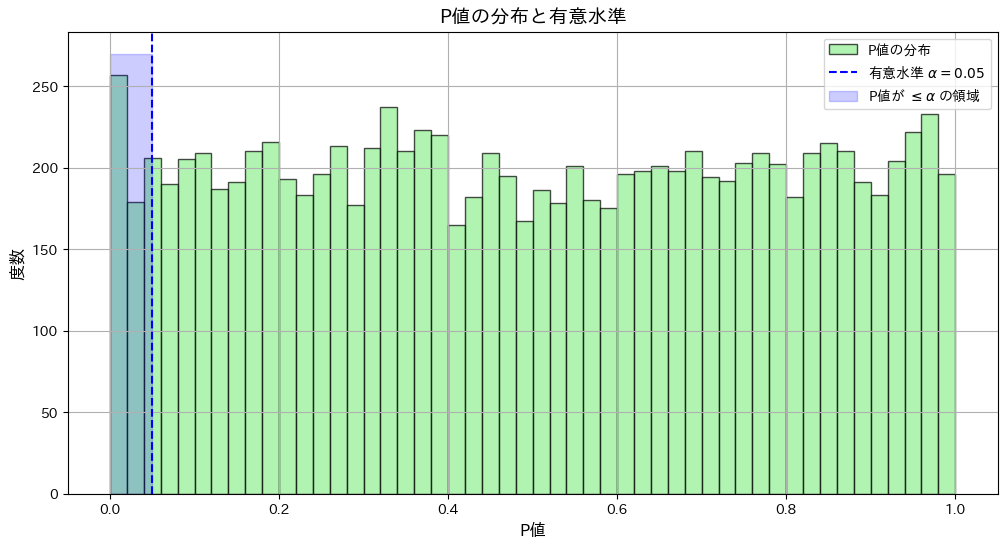
シミュレーションの結果、標本平均![]() が棄却域に入る条件と、P値が有意水準 α以下となる条件が一致しました。
が棄却域に入る条件と、P値が有意水準 α以下となる条件が一致しました。
2015 Q2(1)
標本平均とP値の関係をグラフで描きました。

コード
n=10のときの標本平均![]() とP値の関係をグラフで示します。また
とP値の関係をグラフで示します。また![]() のP値を計算します。
のP値を計算します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 問題の設定
n = 10 # サンプルサイズ
mu_0 = 0 # 帰無仮説の平均
sigma = 1 # 分散1なので標準偏差は1
alpha = 0.05 # 有意水準
critical_value = norm.ppf(1 - alpha) # 上側確率100α%点
threshold = critical_value / np.sqrt(n) # 棄却域の閾値
# 標本平均の値
x_bar_values = np.linspace(0, 1, 100) # 標本平均の範囲
p_values = 1 - norm.cdf((x_bar_values - mu_0) * np.sqrt(n)) # P値を計算
# 指定された x̄ = 0.3, 0.6 の場合の P値
x_bar_special = [0.3, 0.6]
p_values_special = 1 - norm.cdf((np.array(x_bar_special) - mu_0) * np.sqrt(n))
# 結果出力
print("指定された標本平均 x̄ に対応する P値:")
for x, p in zip(x_bar_special, p_values_special):
print(f" 標本平均 x̄ = {x:.1f} の場合の P値: {p:.3f}")
# グラフの描画
plt.figure(figsize=(8, 5))
plt.plot(x_bar_values, p_values, label="P値の挙動", color="orange")
plt.axhline(y=alpha, color="red", linestyle="--", label=f"有意水準 α={alpha}")
plt.scatter(x_bar_special, p_values_special, color="blue", label="指定点 (0.3, 0.6)")
for x, p in zip(x_bar_special, p_values_special):
plt.text(x, p, f"({x:.1f}, {p:.3f})", fontsize=10, color="blue")
plt.xlabel("標本平均 $\\bar{x}$", fontsize=12)
plt.ylabel("P値", fontsize=12)
plt.title("P値の挙動 (標本平均 $\\bar{x}$ の範囲)", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()指定された標本平均 x̄ に対応する P値:
標本平均 x̄ = 0.3 の場合の P値: 0.171
標本平均 x̄ = 0.6 の場合の P値: 0.029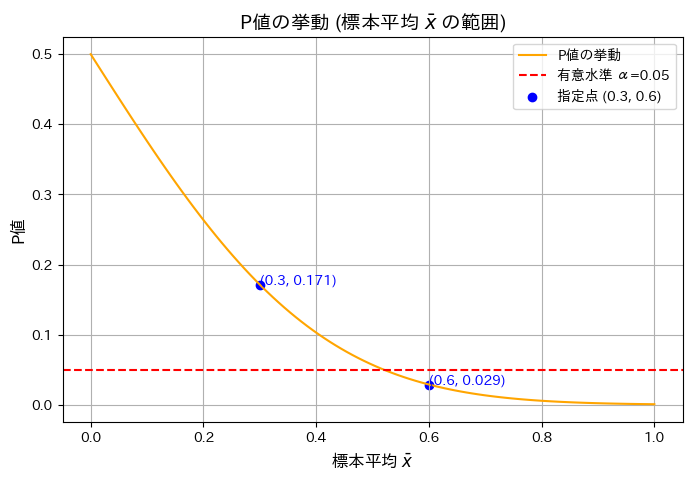
グラフの概形が描けました。標本平均![]() が大きくなるにつれてP値が減少することを確認しました。
が大きくなるにつれてP値が減少することを確認しました。