ホーム » 適合度
「適合度」カテゴリーアーカイブ
2014 Q5(4)
テレビ番組の視聴満足回数の調査で満足と答えた回数のそれぞれ人数の適合度検定を実施し適合を判断する手順を述べました。

コード
多項確率![]() が、
が、![]() に忠実に基づく場合と、各番組または各回答者の満足度が異なるモデルにおいて、カイ二乗統計量、尤度比統計量、およびp-値を計算し、モデルの適合性を比較します。
に忠実に基づく場合と、各番組または各回答者の満足度が異なるモデルにおいて、カイ二乗統計量、尤度比統計量、およびp-値を計算し、モデルの適合性を比較します。
import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
# シミュレーションの設定
n = 100 # 回答者数
p_true = 0.6 # 真の成功確率(忠実なモデル)
categories = np.arange(5) # カテゴリ (0~4)
n_simulations = 1000 # シミュレーション回数
# 忠実なモデルの確率 q_j
qj_true = [np.math.comb(4, j) * (p_true ** j) * ((1 - p_true) ** (4 - j)) for j in categories]
# 統計量を記録するリスト
chi_squared_true = []
likelihood_ratio_true = []
chi_squared_noisy_program = []
likelihood_ratio_noisy_program = []
chi_squared_noisy_responder = []
likelihood_ratio_noisy_responder = []
# 二項分布に従わない (qj_noisy_program): q_j をランダムに変更してズラす
qj_noisy_program = np.array(qj_true) + np.random.uniform(-0.1, 0.1, size=len(qj_true))
qj_noisy_program = np.clip(qj_noisy_program, 0, None) # 確率が0未満にならないようにする
qj_noisy_program = qj_noisy_program / np.sum(qj_noisy_program) # 確率なので正規化
# 各回答者の満足度が異なる場合(qj_noisy_responder)をランダム設定
p_responders = np.random.uniform(0.35, 0.85, size=n)
qj_noisy_responder = np.zeros(len(categories))
for p in p_responders:
qj_responder = [np.math.comb(4, j) * (p ** j) * ((1 - p) ** (4 - j)) for j in categories]
qj_noisy_responder += qj_responder
qj_noisy_responder /= np.sum(qj_noisy_responder)
# シミュレーション開始
for _ in range(n_simulations):
# 忠実なモデル(均一)
obs_true = np.random.multinomial(n, qj_true)
exp_true = n * np.array(qj_true)
chi2_stat_true = np.sum((obs_true - exp_true) ** 2 / exp_true) # カイ二乗統計量
likelihood_stat_true = 2 * np.sum(obs_true * np.log(obs_true / exp_true, where=(obs_true > 0))) # 尤度比統計量
chi_squared_true.append(chi2_stat_true)
likelihood_ratio_true.append(likelihood_stat_true)
# 各番組の満足度が異なる場合
obs_noisy_program = np.random.multinomial(n, qj_noisy_program)
exp_noisy_program = n * np.array(qj_true)
chi2_stat_noisy_program = np.sum((obs_noisy_program - exp_noisy_program) ** 2 / exp_noisy_program) # カイ二乗統計量
likelihood_stat_noisy_program = 2 * np.sum(obs_noisy_program * np.log(obs_noisy_program / exp_noisy_program, where=(obs_noisy_program > 0))) # 尤度比統計量
chi_squared_noisy_program.append(chi2_stat_noisy_program)
likelihood_ratio_noisy_program.append(likelihood_stat_noisy_program)
# 各回答者の満足度が異なる場合
obs_noisy_responder = np.random.multinomial(n, qj_noisy_responder)
exp_noisy_responder = n * np.array(qj_true)
chi2_stat_noisy_responder = np.sum((obs_noisy_responder - exp_noisy_responder) ** 2 / exp_noisy_responder) # カイ二乗統計量
likelihood_stat_noisy_responder = 2 * np.sum(obs_noisy_responder * np.log(obs_noisy_responder / exp_noisy_responder, where=(obs_noisy_responder > 0))) # 尤度比統計量
chi_squared_noisy_responder.append(chi2_stat_noisy_responder)
likelihood_ratio_noisy_responder.append(likelihood_stat_noisy_responder)
# 平均値を計算
mean_chi2_true = np.mean(chi_squared_true)
mean_likelihood_true = np.mean(likelihood_ratio_true)
mean_chi2_noisy_program = np.mean(chi_squared_noisy_program)
mean_likelihood_noisy_program = np.mean(likelihood_ratio_noisy_program)
mean_chi2_noisy_responder = np.mean(chi_squared_noisy_responder)
mean_likelihood_noisy_responder = np.mean(likelihood_ratio_noisy_responder)
# 各統計量に対応するp値を計算
p_value_chi2_true = 1 - chi2.cdf(mean_chi2_true, df=3)
p_value_likelihood_true = 1 - chi2.cdf(mean_likelihood_true, df=3)
p_value_chi2_noisy_program = 1 - chi2.cdf(mean_chi2_noisy_program, df=3)
p_value_likelihood_noisy_program = 1 - chi2.cdf(mean_likelihood_noisy_program, df=3)
p_value_chi2_noisy_responder = 1 - chi2.cdf(mean_chi2_noisy_responder, df=3)
p_value_likelihood_noisy_responder = 1 - chi2.cdf(mean_likelihood_noisy_responder, df=3)
# 結果の出力
print(f"忠実なモデル(均一)の平均カイ二乗統計量: {mean_chi2_true:.4f}, 平均p値: {p_value_chi2_true:.4f}")
print(f"忠実なモデル(均一)の平均尤度比統計量: {mean_likelihood_true:.4f}, 平均p値: {p_value_likelihood_true:.4f}")
print(f"各番組の満足度が異なる場合の平均カイ二乗統計量: {mean_chi2_noisy_program:.4f}, 平均p値: {p_value_chi2_noisy_program:.4f}")
print(f"各番組の満足度が異なる場合の平均尤度比統計量: {mean_likelihood_noisy_program:.4f}, 平均p値: {p_value_likelihood_noisy_program:.4f}")
print(f"各回答者の満足度が異なる場合の平均カイ二乗統計量: {mean_chi2_noisy_responder:.4f}, 平均p値: {p_value_chi2_noisy_responder:.4f}")
print(f"各回答者の満足度が異なる場合の平均尤度比統計量: {mean_likelihood_noisy_responder:.4f}, 平均p値: {p_value_likelihood_noisy_responder:.4f}")
# カイ二乗分布のPDFを計算
x = np.linspace(0, 20, 500) # x軸の範囲
pdf = chi2.pdf(x, df=3) # 自由度3のPDF
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(x, pdf, label="自由度3のカイ二乗分布", linewidth=2)
plt.axvline(mean_chi2_true, color="blue", linestyle="--", label=f"忠実モデルのカイ二乗: {mean_chi2_true:.2f}")
plt.axvline(mean_likelihood_true, color="cyan", linestyle="--", label=f"忠実モデルの尤度比: {mean_likelihood_true:.2f}")
plt.axvline(mean_chi2_noisy_program, color="green", linestyle="--", label=f"番組ごとに異なるカイ二乗: {mean_chi2_noisy_program:.2f}")
plt.axvline(mean_likelihood_noisy_program, color="lime", linestyle="--", label=f"番組ごとに異なる尤度比: {mean_likelihood_noisy_program:.2f}")
plt.axvline(mean_chi2_noisy_responder, color="red", linestyle="--", label=f"回答者ごとに異なるカイ二乗: {mean_chi2_noisy_responder:.2f}")
plt.axvline(mean_likelihood_noisy_responder, color="magenta", linestyle="--", label=f"回答者ごとに異なる尤度比: {mean_likelihood_noisy_responder:.2f}")
plt.xlabel("$X^2$ 値", fontsize=12)
plt.ylabel
plt.ylabel("確率密度", fontsize=12)
plt.title("自由度3のカイ二乗分布と統計量", fontsize=14)
plt.legend(fontsize=12) # ここで凡例を表示
plt.grid(alpha=0.5)
plt.show()忠実なモデル(均一)の平均カイ二乗統計量: 4.1751, 平均p値: 0.2432
忠実なモデル(均一)の平均尤度比統計量: 4.3247, 平均p値: 0.2285
各番組の満足度が異なる場合の平均カイ二乗統計量: 13.2002, 平均p値: 0.0042
各番組の満足度が異なる場合の平均尤度比統計量: 16.4412, 平均p値: 0.0009
各回答者の満足度が異なる場合の平均カイ二乗統計量: 10.3066, 平均p値: 0.0161
各回答者の満足度が異なる場合の平均尤度比統計量: 8.5302, 平均p値: 0.0362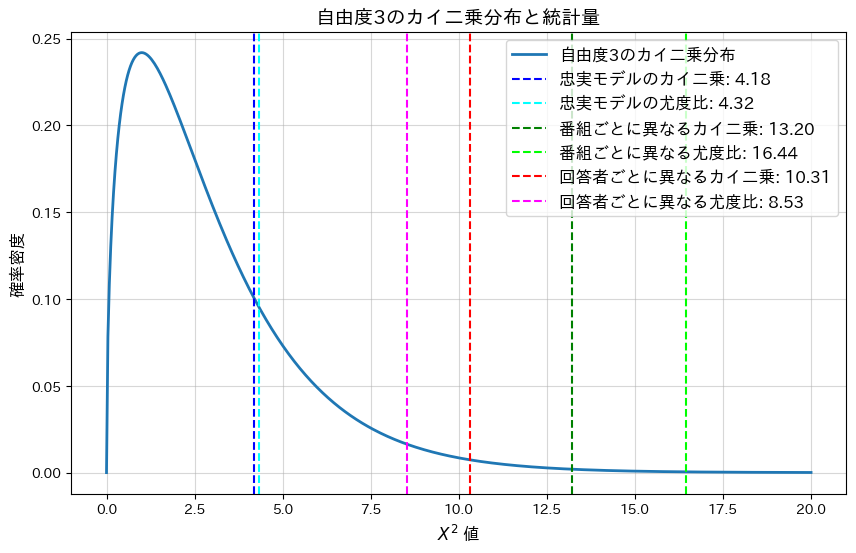
忠実なモデルの平均p-値は大きく、モデルによく適合していることが分かります。一方、各番組または各回答者の満足度が異なるモデルではp-値が0.05以下となり、モデルがデータに適合していないことが分かります。
2014 Q5(3)
テレビ番組の視聴満足回数の調査で満足と答えた回数のそれぞれ人数の適合度検定のための尤度比検定量と自由度を求めました。

コード
多項確率![]() が、
が、![]() に忠実に基づく場合と、ランダムにノイズを加えた(ズレた)場合についてシミュレーションを行い、尤度比統計量とp-値を計算して比較します。
に忠実に基づく場合と、ランダムにノイズを加えた(ズレた)場合についてシミュレーションを行い、尤度比統計量とp-値を計算して比較します。
# 2014 Q5(3) 2025.1.17
import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
# シミュレーションの設定
n = 100 # 人数
p_true = 0.6 # 真の成功確率
categories = np.arange(5) # カテゴリ (0~4)
n_simulations = 1000 # シミュレーション回数
# 二項分布モデルに基づく q_j の計算 (忠実な設定)
qj_true = [np.math.comb(4, j) * (p_true ** j) * ((1 - p_true) ** (4 - j)) for j in categories]
# 二項分布に従わない (qj_noisy): q_j をランダムに変更してズラす
qj_noisy = np.array(qj_true) + np.random.uniform(-0.1, 0.1, size=len(qj_true))
qj_noisy = np.clip(qj_noisy, 0, None) # 確率が0未満にならないようにする
qj_noisy = qj_noisy / np.sum(qj_noisy) # 確率なので正規化
# 尤度比統計量を記録するリスト
likelihood_ratio_true = []
p_values_true = []
likelihood_ratio_noisy = []
p_values_noisy = []
for _ in range(n_simulations):
# 忠実なモデルの観測データ
obs_true = np.random.multinomial(n, qj_true)
exp_true = n * np.array(qj_true)
likelihood_stat_true = 2 * np.sum(obs_true * np.log(obs_true / exp_true, where=(obs_true > 0)))
p_val_true = 1 - chi2.cdf(likelihood_stat_true, df=3) # 自由度 = カテゴリ数 - 1 - 推定パラメータ数
likelihood_ratio_true.append(likelihood_stat_true)
p_values_true.append(p_val_true)
# ズレたモデルの観測データ
obs_noisy = np.random.multinomial(n, qj_noisy)
exp_noisy = n * np.array(qj_true) # 忠実な期待値を使用
likelihood_stat_noisy = 2 * np.sum(obs_noisy * np.log(obs_noisy / exp_noisy, where=(obs_noisy > 0)))
p_val_noisy = 1 - chi2.cdf(likelihood_stat_noisy, df=3)
likelihood_ratio_noisy.append(likelihood_stat_noisy)
p_values_noisy.append(p_val_noisy)
# 平均尤度比統計量を計算
mean_likelihood_true = np.mean(likelihood_ratio_true)
mean_likelihood_noisy = np.mean(likelihood_ratio_noisy)
# カイ二乗分布のPDFを計算
x = np.linspace(0, 20, 500) # x軸の範囲
pdf = chi2.pdf(x, df=3) # 自由度3のPDF
# 結果の出力
print(f"忠実なモデルの平均尤度比統計量: {mean_likelihood_true:.4f}")
print(f"忠実なモデルの平均p値: {np.mean(p_values_true):.4f}")
print(f"ズレたモデルの平均尤度比統計量: {mean_likelihood_noisy:.4f}")
print(f"ズレたモデルの平均p値: {np.mean(p_values_noisy):.4f}")
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(x, pdf, label="自由度3のカイ二乗分布", linewidth=2)
plt.axvline(mean_likelihood_true, color="blue", linestyle="--", label=f"忠実モデルの平均: {mean_likelihood_true:.2f}")
plt.axvline(mean_likelihood_noisy, color="red", linestyle="--", label=f"ズレモデルの平均: {mean_likelihood_noisy:.2f}")
plt.xlabel("$X^2$ 値", fontsize=12)
plt.ylabel("確率密度", fontsize=12)
plt.title("自由度3のカイ二乗分布と平均尤度比統計量", fontsize=14)
plt.legend(fontsize=12)
plt.grid(alpha=0.5)
plt.show()忠実なモデルの平均尤度比統計量: 3.9418
忠実なモデルの平均p値: 0.3909
ズレたモデルの平均尤度比統計量: 16.7360
ズレたモデルの平均p値: 0.0081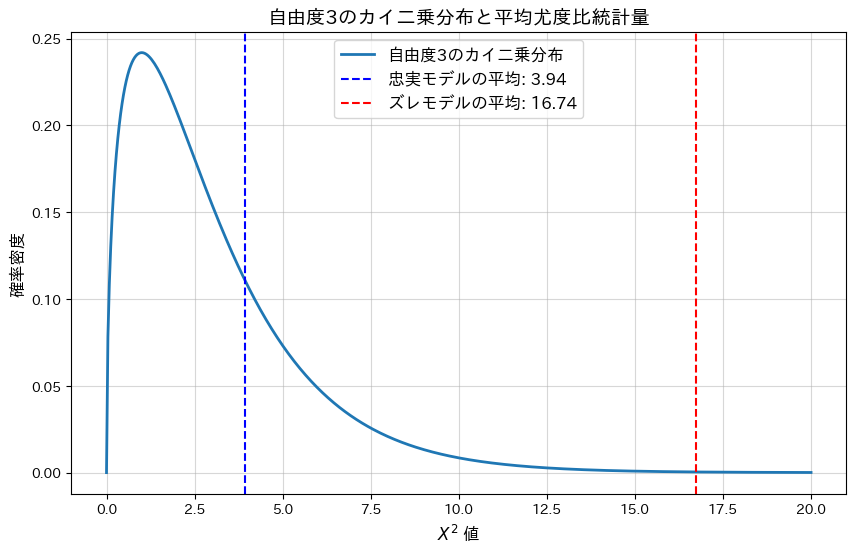
忠実なモデルの平均p-値は大きく、モデルによく適合していることが分かります。一方、ランダムにノイズを加えた(ズレた)モデルではp-値が0.05以下となり、モデルがデータに適合していないことが分かります。
2014 Q5(2)
テレビ番組の視聴満足回数の調査で満足と答えた回数のそれぞれ人数の適合度カイ二乗統計量と自由度を求めました。

コード
多項確率![]() が、
が、![]() に忠実に基づく場合と、ランダムにノイズを加えた(ズレた)場合についてシミュレーションを行い、適合度カイ二乗統計量とp-値を計算して比較します。
に忠実に基づく場合と、ランダムにノイズを加えた(ズレた)場合についてシミュレーションを行い、適合度カイ二乗統計量とp-値を計算して比較します。
# 2014 Q5(2) 2025.1.16
import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
# シミュレーションの設定
n = 100 # 人数
p_true = 0.6 # 真の成功確率
categories = np.arange(5) # カテゴリ (0~4)
n_simulations = 1000 # シミュレーション回数
# 二項分布モデルに基づく q_j の計算 (忠実な設定)
qj_true = [np.math.comb(4, j) * (p_true ** j) * ((1 - p_true) ** (4 - j)) for j in categories]
# 二項分布に従わない (qj_noisy): q_j をランダムに変更してズラす
qj_noisy = np.array(qj_true) + np.random.uniform(-0.1, 0.1, size=len(qj_true))
qj_noisy = np.clip(qj_noisy, 0, None) # 確率が0未満にならないようにする
qj_noisy = qj_noisy / np.sum(qj_noisy) # 確率なので正規化
# カイ二乗統計量と p 値を記録するリスト
chi_squared_true = []
p_values_true = []
chi_squared_noisy = []
p_values_noisy = []
for _ in range(n_simulations):
# 忠実なモデルの観測データ
obs_true = np.random.multinomial(n, qj_true)
exp_true = n * np.array(qj_true)
chi2_stat_true = np.sum((obs_true - exp_true) ** 2 / exp_true)
p_val_true = 1 - chi2.cdf(chi2_stat_true, df=3) # 自由度 = カテゴリ数 - 1 - 推定パラメータ数
chi_squared_true.append(chi2_stat_true)
p_values_true.append(p_val_true)
# ズレたモデルの観測データ
obs_noisy = np.random.multinomial(n, qj_noisy)
exp_noisy = n * np.array(qj_true) # 忠実な期待値を使用
chi2_stat_noisy = np.sum((obs_noisy - exp_noisy) ** 2 / exp_noisy)
p_val_noisy = 1 - chi2.cdf(chi2_stat_noisy, df=3)
chi_squared_noisy.append(chi2_stat_noisy)
p_values_noisy.append(p_val_noisy)
# 平均カイ二乗統計量を計算
mean_chi2_true = np.mean(chi_squared_true)
mean_chi2_noisy = np.mean(chi_squared_noisy)
# カイ二乗分布のPDFを計算
x = np.linspace(0, 20, 500) # x軸の範囲
pdf = chi2.pdf(x, df=3) # 自由度3のPDF
# 結果の出力
print(f"忠実なモデルの平均カイ二乗統計量: {mean_chi2_true:.4f}")
print(f"忠実なモデルの平均p値: {np.mean(p_values_true):.4f}")
print(f"ズレたモデルの平均カイ二乗統計量: {mean_chi2_noisy:.4f}")
print(f"ズレたモデルの平均p値: {np.mean(p_values_noisy):.4f}")
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(x, pdf, label="自由度3のカイ二乗分布", linewidth=2)
plt.axvline(mean_chi2_true, color="blue", linestyle="--", label=f"忠実モデルの平均: {mean_chi2_true:.2f}")
plt.axvline(mean_chi2_noisy, color="red", linestyle="--", label=f"ズレモデルの平均: {mean_chi2_noisy:.2f}")
plt.xlabel("$X^2$ 値", fontsize=12)
plt.ylabel("確率密度", fontsize=12)
plt.title("自由度3のカイ二乗分布と平均カイ二乗統計量", fontsize=14)
plt.legend(fontsize=12)
plt.grid(alpha=0.5)
plt.show()忠実なモデルの平均カイ二乗統計量: 3.8112
忠実なモデルの平均p値: 0.4026
ズレたモデルの平均カイ二乗統計量: 13.4317
ズレたモデルの平均p値: 0.0236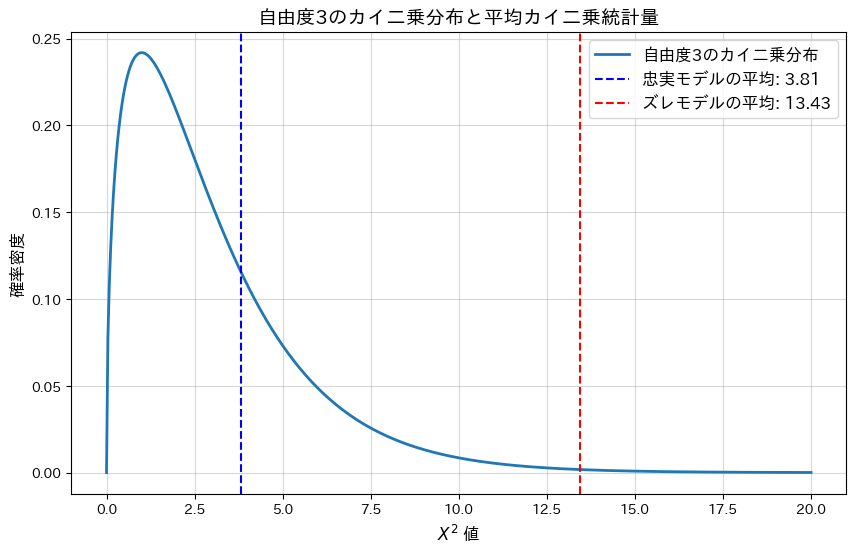
忠実なモデルの平均p-値は大きく、モデルによく適合していることが分かります。一方、ランダムにノイズを加えた(ズレた)モデルではp-値が0.05以下となり、モデルがデータに適合していないことが分かります。