2014 Q2(5)
n個の一様分布の順序統計量の期待値を求めました。
コード
サンプルサイズn=5として、一様分布の順序統計量![]() をシミュレーションし、その確率密度の形状を確認するとともに、期待値がどのようになるか確かめます。
をシミュレーションし、その確率密度の形状を確認するとともに、期待値がどのようになるか確かめます。
# 2014 Q2(5) 2024.1.4
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
n_simulations = 10**6 # サンプルサイズ
n = 5 # サンプルサイズ (n個の確率変数)
# 一様分布からサンプリング
U = np.random.uniform(0, 1, (n_simulations, n))
# PDF (確率密度関数) および期待値をプロット
j_values = range(1, n + 1) # j を 1 から n まで変化させる
plt.figure(figsize=(14, 8))
colors = ['blue', 'orange', 'green', 'red', 'purple'] # 色の設定
for idx, j in enumerate(j_values):
# j 番目の順序統計量を取得
U_j = np.sort(U, axis=1)[:, j-1]
# 理論値のPDFを計算
u = np.linspace(0, 1, 1000)
pdf_theory = (n * np.math.comb(n-1, j-1)) * (u**(j-1)) * ((1-u)**(n-j))
# ヒストグラム (シミュレーション結果)
plt.hist(U_j, bins=50, density=True, alpha=0.5, label=f'j = {j} (シミュレーション)', color=colors[idx])
# 理論値のPDFをプロット
plt.plot(u, pdf_theory, linestyle='--', color=colors[idx], label=f'j = {j} (理論)')
# 理論値の期待値を直線で追加
expected_value = j / (n + 1)
plt.axvline(x=expected_value, color=colors[idx], linestyle=':', label=f'j = {j} 期待値 = {expected_value:.2f}')
# グラフ装飾
plt.title('順序統計量 U_(j) の PDF と期待値 (理論 vs シミュレーション)', fontsize=16)
plt.xlabel('値', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()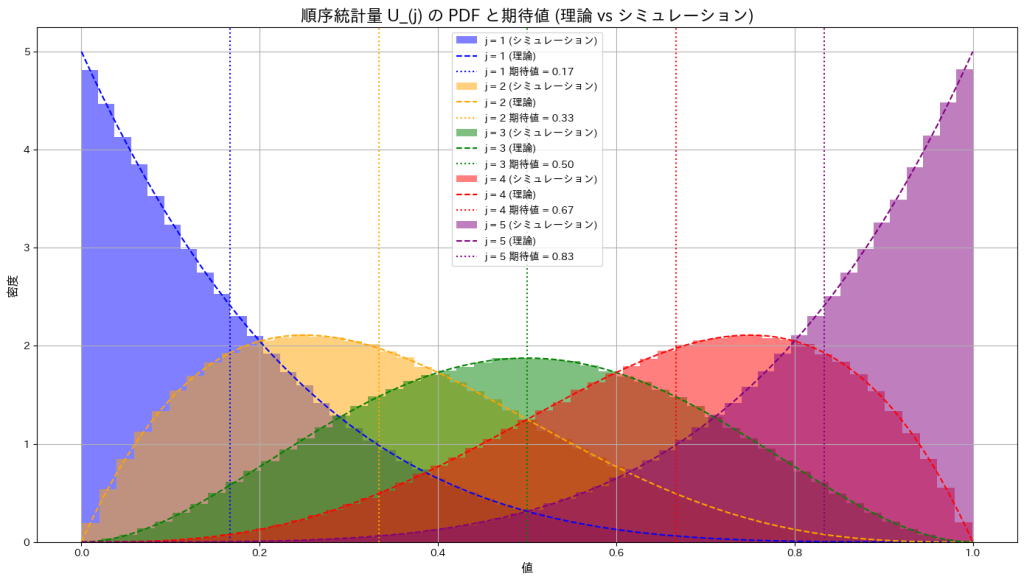
一様分布の順序統計量![]() の確率密度は、jが小さいときには左に寄り、jが大きくなると右に寄る形状を示します。また期待値はj/(n+1)であるため0~1の範囲をn+1で均等に分割した値に一致することが確認できました。
の確率密度は、jが小さいときには左に寄り、jが大きくなると右に寄る形状を示します。また期待値はj/(n+1)であるため0~1の範囲をn+1で均等に分割した値に一致することが確認できました。
2014 Q1(3)
一様分布の指数を取るn個の確率変数のうち特定の一つが最大値をとる確率を求めました。
コード
与式は![]() と考え、
と考え、![]() とした場合の
とした場合の![]() をシミュレーションで計算し、理論値と比較します。
をシミュレーションで計算し、理論値と比較します。
# 2014 Q1(3) 2024.12.30
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
n_simulations = 10**6
# 確率変数の数とパラメータの設定
n = 5
alphas = [2, 3, 4, 5, 6] # α1, α2, ..., αn
# 一様分布からサンプリング
U = np.random.uniform(0, 1, (n_simulations, n))
X = U**np.array(alphas)
# 確率変数 Z を計算 (Z = X1 - max(X2, ..., Xn))
Z_diff = X[:, 0] - np.max(X[:, 1:], axis=1)
# Z の累積分布関数 (CDF) を計算
z_sorted = np.sort(Z_diff)
cdf_Z = np.arange(1, len(z_sorted) + 1) / len(z_sorted)
# Z = 0 の累積確率を計算
cumulative_prob_at_zero = cdf_Z[np.searchsorted(z_sorted, 0)]
# 理論値の計算
theoretical_prob = (1 / alphas[0]) / sum(1 / alpha for alpha in alphas)
# 結果を出力
print(f"Z = 0 における続繁確率: {cumulative_prob_at_zero:.3f}")
print(f"シミュレーション結果: P(X1 > max(X2, ..., Xn)) = {1 - cumulative_prob_at_zero:.6f}")
print(f"理論値: P(X1 > max(X2, ..., Xn)) = {theoretical_prob:.6f}")
print(f"誤差: {abs((1 - cumulative_prob_at_zero) - theoretical_prob):.6f}")
# PDF および CDF のプロット (PDF にも Z = 0 の赤い線を追加)
plt.figure(figsize=(14, 6))
# PDF
plt.subplot(1, 2, 1)
plt.hist(Z_diff, bins=100, density=True, alpha=0.7, label=r'$Z = X_1 - \max(X_2, ..., X_n)$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)') # Z = 0 の赤い線を追加
plt.title('Z = X1 - max(X2, ..., Xn) の確率密度関数 (PDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()
# CDF
plt.subplot(1, 2, 2)
plt.plot(z_sorted, cdf_Z, label=r'$Z = X_1 - \max(X_2, ..., X_n)$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)') # Z = 0 の赤い線
plt.text(0.05, cumulative_prob_at_zero, f'{cumulative_prob_at_zero:.3f}', color='red', fontsize=12)
plt.title('Z = X1 - max(X2, ..., Xn) の続繁分布関数 (CDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('続繁確率', fontsize=12)
plt.legend()
plt.tight_layout()
plt.show()Z = 0 における続繁確率: 0.655
シミュレーション結果: P(X1 > max(X2, ..., Xn)) = 0.345030
理論値: P(X1 > max(X2, ..., Xn)) = 0.344828
誤差: 0.000202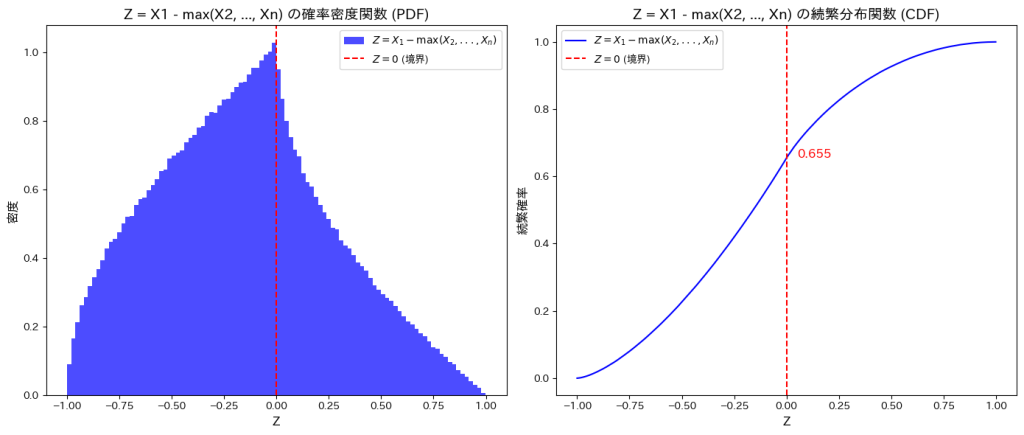
![]() はシミュレーションの結果、理論値と一致しました。
はシミュレーションの結果、理論値と一致しました。
2014 Q1(2)
一様分布の指数を取る三つの確率変数のうち特定の一つが最大値をとる確率を求めました。

コード
与式は![]() と考え、
と考え、![]() とした場合の
とした場合の![]() をシミュレーションで計算し、理論値と比較します。
をシミュレーションで計算し、理論値と比較します。
# 2014 Q1(2) 2024.12.29
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
n_simulations = 10**6
# 一様分布からサンプリング
U = np.random.uniform(0, 1, n_simulations)
V = np.random.uniform(0, 1, n_simulations)
W = np.random.uniform(0, 1, n_simulations)
# パラメータの設定
alpha, beta, gamma = 2, 3, 4
# X, Y, Z の計算
X = U**alpha
Y = V**beta
Z = W**gamma
# 確率変数 Z を計算 (例: Z = X - max(Y, Z))
Z_diff = X - np.maximum(Y, Z)
# Z の累積分布関数 (CDF) を計算
z_sorted = np.sort(Z_diff)
cdf_Z = np.arange(1, len(z_sorted) + 1) / len(z_sorted)
# Z = 0 の累積確率を計算
cumulative_prob_at_zero = cdf_Z[np.searchsorted(z_sorted, 0)]
# 理論値の計算
theoretical_prob = (1 / alpha) / (1 / alpha + 1 / beta + 1 / gamma)
# 結果を出力
print(f"Z = 0 における累積確率: {cumulative_prob_at_zero:.3f}")
print(f"シミュレーション結果: P(X > max(Y, Z)) = {1 - cumulative_prob_at_zero:.6f}")
print(f"理論値: P(X > max(Y, Z)) = {theoretical_prob:.6f}")
print(f"誤差: {abs((1 - cumulative_prob_at_zero) - theoretical_prob):.6f}")
# PDF および CDF のプロット (PDF にも Z = 0 の赤い線を追加)
plt.figure(figsize=(14, 6))
# PDF
plt.subplot(1, 2, 1)
plt.hist(Z_diff, bins=100, density=True, alpha=0.7, label=r'$Z = X - \max(Y, Z)$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)') # Z = 0 の赤い線を追加
plt.title('Z = X - max(Y, Z) の確率密度関数 (PDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()
# CDF
plt.subplot(1, 2, 2)
plt.plot(z_sorted, cdf_Z, label=r'$Z = X - \max(Y, Z)$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)') # Z = 0 の赤い線
plt.text(0.05, cumulative_prob_at_zero, f'{cumulative_prob_at_zero:.3f}', color='red', fontsize=12)
plt.title('Z = X - max(Y, Z) の累積分布関数 (CDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('累積確率', fontsize=12)
plt.legend()
plt.tight_layout()
plt.show()Z = 0 における累積確率: 0.538
シミュレーション結果: P(X > max(Y, Z)) = 0.462111
理論値: P(X > max(Y, Z)) = 0.461538
誤差: 0.000573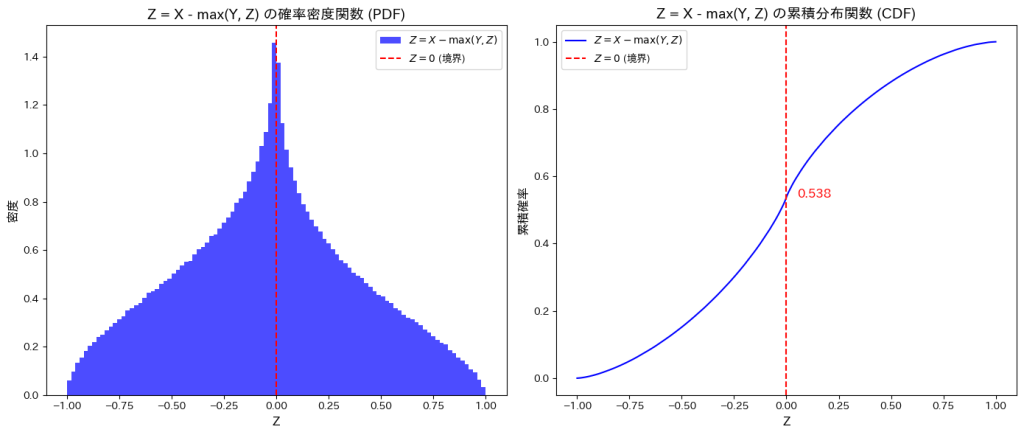
![]() はシミュレーションの結果、理論値と一致しました。
はシミュレーションの結果、理論値と一致しました。
2014 Q1(1)
一様分布の指数を取る二つの確率変数の大小が決まっている場合の確率を条件付確率の期待値を取ることで求めました。

コード
XとYの頻度分布を3Dプロットで可視化してみます。
# 2014 Q1(1) 2024.12.28
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# シミュレーションの設定
n_simulations = 10**5 # サンプルサイズ
# 一様分布からサンプリング
U = np.random.uniform(0, 1, n_simulations)
V = np.random.uniform(0, 1, n_simulations)
# X, Y の計算
X = U**2
Y = V**3
# 3Dプロット
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 2次元ヒストグラムを計算
hist, xedges, yedges = np.histogram2d(X, Y, bins=50, density=True)
# 座標軸を作成
xpos, ypos = np.meshgrid(xedges[:-1], yedges[:-1], indexing="ij")
xpos = xpos.ravel()
ypos = ypos.ravel()
zpos = np.zeros_like(xpos)
# 棒の高さ
dx = dy = 0.02
dz = hist.ravel()
# 色分け: X > Y (緑), X = Y (黄色), X < Y (青)
tolerance = 0.01 # 許容範囲を指定して X = Y の近似を表現
colors = np.where(
np.abs(xpos - ypos) < tolerance, 'yellow',
np.where(xpos > ypos, 'green', 'blue')
)
# 3Dバーを描画
ax.bar3d(xpos, ypos, zpos, dx, dy, dz, zsort='average', alpha=0.7, color=colors)
# ラベルとタイトル
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('頻度', labelpad=-10) # ラベルの位置を調整
#ax.set_title(r'$X > Y$ (緑), $X = Y$ (黄色), $X < Y$ (青)', fontsize=14)
#ax.set_title(r'$X$ と $Y$ の出現頻度', fontsize=14)
ax.set_title(r'$X$ と $Y$ の出現頻度(組)', fontsize=14)
# 凡例
legend_handles = [
plt.Line2D([0], [0], color='green', lw=4, label=r'$X > Y$ (緑)'),
plt.Line2D([0], [0], color='yellow', lw=4, label=r'$X = Y$ (黄色)'),
plt.Line2D([0], [0], color='blue', lw=4, label=r'$X < Y$ (青)')
]
ax.legend(handles=legend_handles, loc='upper left', bbox_to_anchor=(1.05, 1), fontsize=10)
# カメラビュー
ax.view_init(elev=30, azim=45)
plt.tight_layout()
plt.show()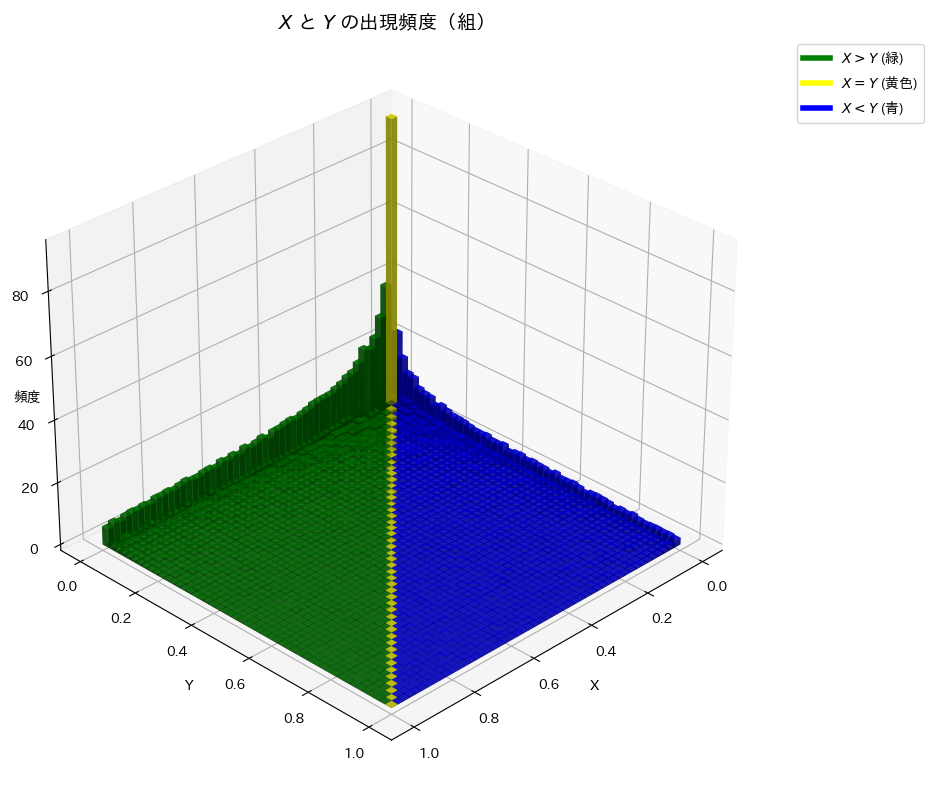
X>Yの領域は、X<Yの領域と比べて出現頻度が高いようです。
次に、XとYの大小関係を確認するために確率変数Z=X-Yを同に導入し、その確率密度と累積分布をシミュレーションにより求め、P(X>Y)を計算してみます。
# 2014 Q1(1) 2024.12.28
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
np.random.seed(42)
n_simulations = 10**6
# 一様分布からサンプリング
U = np.random.uniform(0, 1, n_simulations)
V = np.random.uniform(0, 1, n_simulations)
# X, Y の計算
X = U**2
Y = V**3
# Z = X - Y を計算
Z = X - Y
# Z の累積分布関数 (CDF) を計算
z_sorted = np.sort(Z)
cdf_Z = np.arange(1, len(z_sorted) + 1) / len(z_sorted)
# Z = 0 の累積確率を計算
cumulative_prob_at_zero = cdf_Z[np.searchsorted(z_sorted, 0)]
# 結果を出力
print(f"Z = 0 における累積確率: {cumulative_prob_at_zero:.3f}")
print(f"P(X > Y) = {1 - cumulative_prob_at_zero:.3f}")
# PDF および CDF のプロット (PDF にも Z = 0 の赤い線を追加)
plt.figure(figsize=(14, 6))
# PDF
plt.subplot(1, 2, 1)
plt.hist(Z, bins=100, density=True, alpha=0.7, label=r'$Z = X - Y$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)') # Z = 0 の赤い線を追加
plt.title('Z = X - Y の確率密度関数 (PDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()
# CDF
plt.subplot(1, 2, 2)
plt.plot(z_sorted, cdf_Z, label=r'$Z = X - Y$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)') # Z = 0 の赤い線
plt.text(0.05, cumulative_prob_at_zero, f'{cumulative_prob_at_zero:.3f}', color='red', fontsize=12)
plt.title('Z = X - Y の累積分布関数 (CDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('累積確率', fontsize=12)
plt.legend()
plt.tight_layout()
plt.show()Z = 0 における累積確率: 0.399
P(X > Y) = 0.601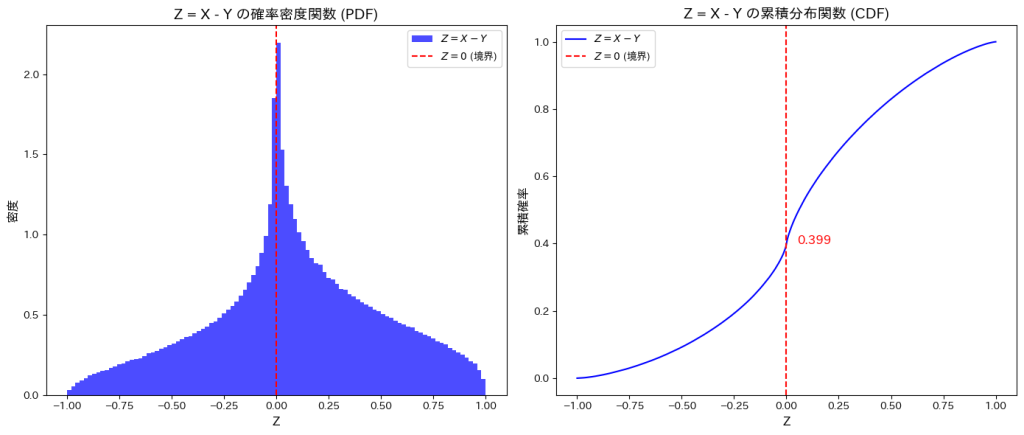
シミュレーションにより求めたP(X>Y)は、理論値と一致することが確認できました。
2017 Q2(4)
二つの不偏推定量の分散の大きさを比較する事でどちらの推定量が望ましいかを調べました。

コード
θ=10,n=20としてシミュレーションを行い、θ’とθ’’の分布を重ねて描画してみます。
# 2017 Q2(4) 2024.11.1
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
n = 20 # サンプルサイズ
num_trials = 1000 # シミュレーションの試行回数
# θ' = 2 * X̄ と θ'' = (n + 1) / n * X_max の推定値を記録するリスト
theta_prime_estimates = []
theta_double_prime_estimates = []
# シミュレーションを実行
for _ in range(num_trials):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# θ' = 2 * X̄ を計算
theta_prime = 2 * np.mean(samples)
theta_prime_estimates.append(theta_prime)
# θ'' = (n + 1) / n * X_max を計算
theta_double_prime = (n + 1) / n * np.max(samples)
theta_double_prime_estimates.append(theta_double_prime)
# ヒストグラムの表示
plt.hist(theta_prime_estimates, bins=30, edgecolor='black', density=True, alpha=0.5, label=r'$\theta\' = 2 \bar{X}$')
plt.hist(theta_double_prime_estimates, bins=30, edgecolor='black', density=True, alpha=0.5, label=r'$\theta\'\' = \frac{n + 1}{n} X_{\max}$')
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel('推定量')
plt.ylabel('密度')
plt.title(r'$\theta\' = 2 \bar{X}$ と $\theta\'\' = \frac{n + 1}{n} X_{\max}$ の分布')
plt.legend()
plt.show()
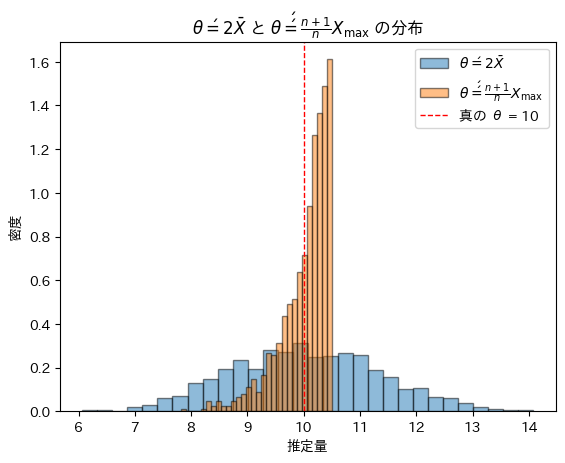
θ’とθ’’は同じ期待(θ)を持つものの横の広がり方が異なりθ’’の分散はθ’の分散よりも小さいことが確認できました。
次にサンプルサイズnを変化させて不偏推定量θ’とθ’’を重ねて描画してみます。
# 2017 Q2(4) 2024.11.1
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
max_n = 100 # 最大サンプルサイズ
num_trials_per_n = 100 # 各サンプルサイズでの試行回数
# 各サンプルサイズにおける θ' と θ'' の平均を記録
theta_prime_means = []
theta_double_prime_means = []
# サンプルサイズ n を 1 から max_n まで増やしながらシミュレーション
for n in range(1, max_n + 1):
theta_prime_estimates = []
theta_double_prime_estimates = []
for _ in range(num_trials_per_n):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# θ' = 2 * X̄ を計算し、その推定値を記録
theta_prime = 2 * np.mean(samples)
theta_prime_estimates.append(theta_prime)
# θ'' = (n + 1) / n * X_max を計算し、その推定値を記録
theta_double_prime = (n + 1) / n * np.max(samples)
theta_double_prime_estimates.append(theta_double_prime)
# 各 n に対する θ' と θ'' の平均を保存
theta_prime_means.append(np.mean(theta_prime_estimates))
theta_double_prime_means.append(np.mean(theta_double_prime_estimates))
# グラフ描画
plt.plot(range(1, max_n + 1), theta_prime_means, label=r'$\mathbb{E}[\theta\']$', color='orange', alpha=0.7)
plt.plot(range(1, max_n + 1), theta_double_prime_means, label=r'$\mathbb{E}[\theta\'\']$', color='saddlebrown', alpha=0.7)
plt.axhline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'サンプルサイズ $n$')
plt.ylabel('推定量の平均')
plt.title(r'サンプルサイズ $n$ と 推定量 $\theta\' = 2 \bar{X}$, $\theta\'\' = \frac{n + 1}{n} X_{\max}$ の関係')
plt.legend()
plt.show()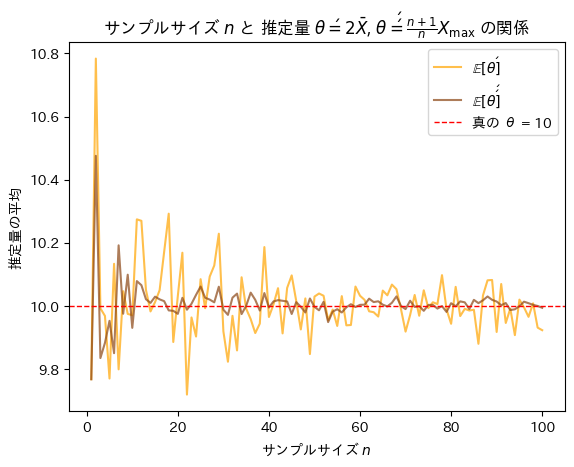
サンプルサイズnが増加するにつれて不偏推定量θ’とθ’’は共に真のθに近づくものの振幅が異なりθ’’の分散はθ’の分散よりも小さいことが確認できました。また収束する速度もθ’’はθ’よりも速いことが確認できました。
2017 Q2(3)
サンプルデータの最大値の(n+1)/n倍が一様分布の上限値の不偏推定量であることの証明をしました。
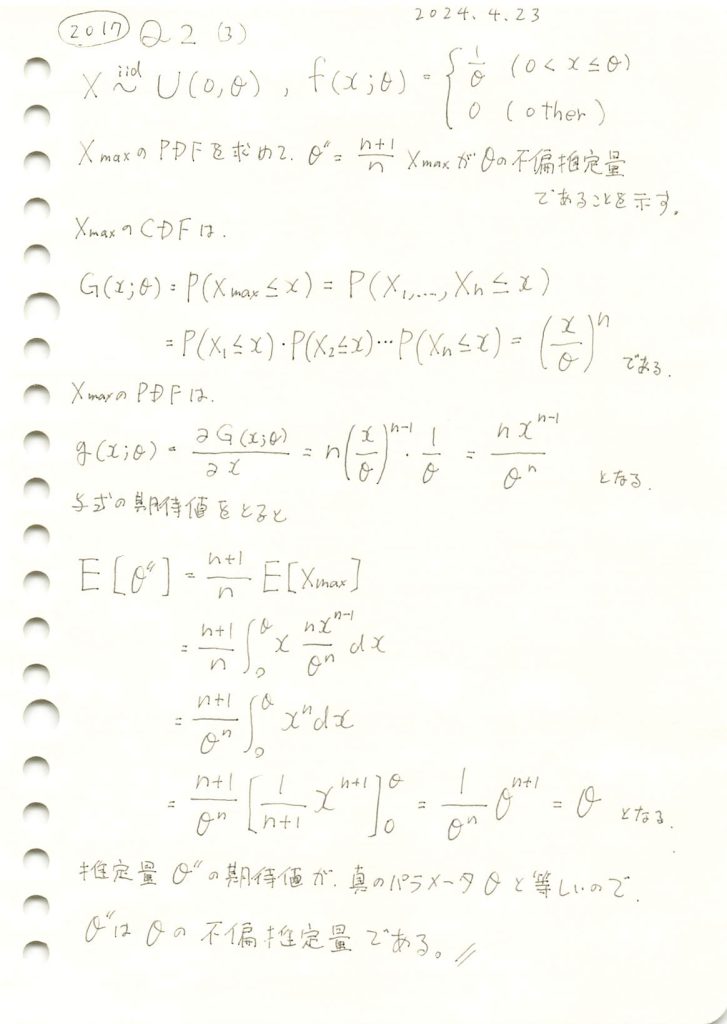
コード
θ=10,n=20としてシミュレーションを行い、θ’’の分布を見てみます。
# 2017 Q2(3) 2024.10.31
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
n = 20 # サンプルサイズ
num_trials = 1000 # シミュレーションの試行回数
# シミュレーションを実行
theta_double_prime_estimates = []
for _ in range(num_trials):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプルの最大値 X_max を計算し、それを用いて θ'' を計算
theta_double_prime = (n + 1) / n * np.max(samples)
theta_double_prime_estimates.append(theta_double_prime)
# θ'' の分布をヒストグラムで表示
plt.hist(theta_double_prime_estimates, bins=30, edgecolor='black', density=True)
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'$\theta\'\' = \frac{n + 1}{n} X_{\max}$')
plt.ylabel('密度')
plt.title(r'$\theta\'\' = \frac{n + 1}{n} X_{\max}$ の分布')
plt.legend()
plt.show()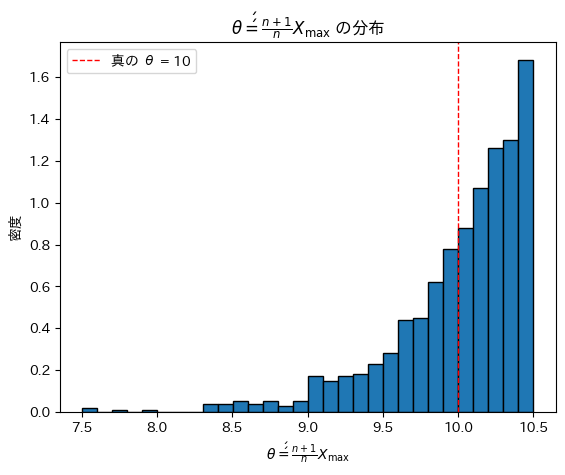
θ’’は、元となるXmaxの分布を右にずらした形状を取っています。期待値は真のθに一致しているようです。
次にサンプルサイズnを変化させて不偏推定量θ’’がどうなるのか確認をします。
# 2017 Q2(3) 2024.10.31
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
max_n = 100 # 最大サンプルサイズ
num_trials_per_n = 100 # 各サンプルサイズでの試行回数
# 各サンプルサイズにおける θ'' の平均を記録
theta_double_prime_means = []
# サンプルサイズ n を 1 から max_n まで増やしながらシミュレーション
for n in range(1, max_n + 1):
theta_double_prime_estimates = []
for _ in range(num_trials_per_n):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプルの最大値 X_max を計算し、それを用いて θ'' を計算
theta_double_prime = (n + 1) / n * np.max(samples)
theta_double_prime_estimates.append(theta_double_prime)
# 各 n に対する θ'' の平均を保存
theta_double_prime_means.append(np.mean(theta_double_prime_estimates))
# グラフ描画
plt.plot(range(1, max_n + 1), theta_double_prime_means, label=r'$\mathbb{E}[\theta\'\']$')
plt.axhline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'サンプルサイズ $n$')
plt.ylabel(r'推定量 $\theta\'\' = \frac{n + 1}{n} X_{\max}$ の平均')
plt.title(r'サンプルサイズ $n$ と $\theta\'\' = \frac{n + 1}{n} X_{\max}$ の関係')
plt.legend()
plt.show()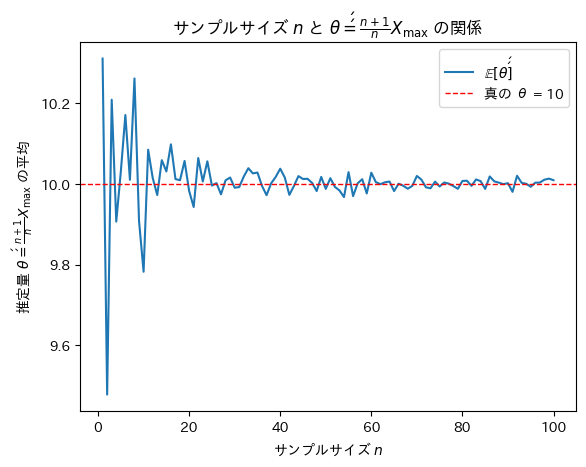
サンプルサイズnが増加するにつれて不偏推定量θ’’は真のθに近づくことが確認できました。
2017 Q2(2)
標本平均の2倍が一様分布の上限値の不偏推定量であることの証明をしました。

コード
θ=10,n=20としてシミュレーションを行い、θ’の分布を見てみます。
# 2017 Q2(2) 2024.10.30
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
theta_true = 10 # 真の θ の値
n = 20 # 1試行あたりのサンプル数
num_trials = 1000 # シミュレーションの試行回数
# シミュレーションを実行
theta_prime_estimates = []
for _ in range(num_trials):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプル平均 X̄ を計算し、それを用いて θ' を計算
theta_prime = 2 * np.mean(samples)
theta_prime_estimates.append(theta_prime)
# θ' の分布をヒストグラムで表示
plt.hist(theta_prime_estimates, bins=30, edgecolor='black', density=True)
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'$\theta\' = 2\bar{X}$')
plt.ylabel('密度')
plt.title(r'$\theta\' = 2\bar{X}$ の分布')
plt.legend()
plt.show()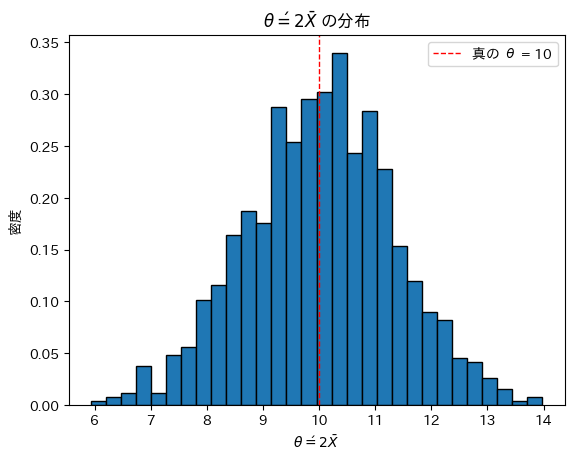
θ’は真のθを中心に左右対称にバラついています。θ’は不偏であるように見えます。
次にサンプルサイズnを変化させて不偏推定量θ’がどうなるのか確認をします。
# 2017 Q2(2) 2024.10.30
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
max_n = 100 # 最大サンプルサイズ
num_trials_per_n = 100 # 各サンプルサイズでの試行回数
# 各サンプルサイズにおける θ' の平均を記録
theta_prime_means = []
# サンプルサイズ n を 1 から max_n まで増やしながらシミュレーション
for n in range(1, max_n + 1):
theta_prime_estimates = []
for _ in range(num_trials_per_n):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプル平均 X̄ を計算し、それを用いて θ' を計算
theta_prime = 2 * np.mean(samples)
theta_prime_estimates.append(theta_prime)
# 各 n に対する θ' の平均を保存
theta_prime_means.append(np.mean(theta_prime_estimates))
# グラフ描画
plt.plot(range(1, max_n + 1), theta_prime_means, label=r'$\mathbb{E}[\theta\']$')
plt.axhline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'サンプルサイズ $n$')
plt.ylabel(r'推定量 $\theta\' = 2 \bar{X}$ の平均')
plt.title(r'サンプルサイズ $n$ と $\theta\' = 2 \bar{X}$ の関係')
plt.legend()
plt.show()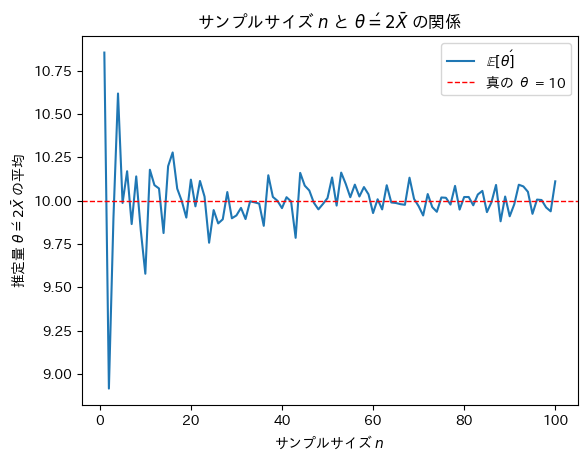
サンプルサイズnが増加するにつれて不偏推定量θ’は真のθに近づくことが確認できました。
2017 Q2(1)
一様分布の上限の最尤推定量を求めました。

コード
θ=10,n=20としてシミュレーションを行い、![]() の分布を見てみます。
の分布を見てみます。
# 2017 Q2(1) 2024.10.29
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
theta_true = 10 # 真の θ の値
n = 20 # 1試行あたりのサンプル数
num_trials = 1000 # シミュレーションの試行回数
# シミュレーションを実行
theta_estimates = []
for _ in range(num_trials):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプルの最大値を推定値 θ_hat として記録
theta_hat = np.max(samples)
theta_estimates.append(theta_hat)
# 推定値の分布をヒストグラムで表示
plt.hist(theta_estimates, bins=30, edgecolor='black', density=True)
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'$\hat{\theta}$')
plt.ylabel('密度')
plt.title(r'$\hat{\theta} = X_{\max}$ の分布')
plt.legend()
plt.show()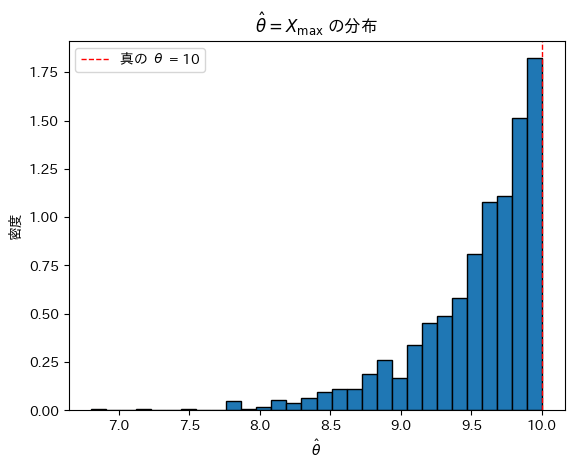
![]() は真のθより大きくならないため、結果としてθよりやや小さな値を取っているように見えます。
は真のθより大きくならないため、結果としてθよりやや小さな値を取っているように見えます。
次にサンプルサイズnを変化させて最尤推定量![]() がどうなるのか確認をします。
がどうなるのか確認をします。
# 2017 Q2(1) 2024.10.29
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
max_n = 100 # 最大サンプルサイズ
num_trials_per_n = 100 # 各サンプルサイズでの試行回数
# 各サンプルサイズにおける θ^ の平均を記録
theta_hat_means = []
# サンプルサイズ n を 1 から max_n まで増やしながらシミュレーション
for n in range(1, max_n + 1):
theta_estimates = []
for _ in range(num_trials_per_n):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプルの最大値を推定値 θ_hat として記録
theta_hat = np.max(samples)
theta_estimates.append(theta_hat)
# 各 n に対する θ^ の平均を保存
theta_hat_means.append(np.mean(theta_estimates))
# グラフ描画
plt.plot(range(1, max_n + 1), theta_hat_means, label=r'$\mathbb{E}[\hat{\theta}]$')
plt.axhline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'サンプルサイズ $n$')
plt.ylabel(r'推定量 $\hat{\theta}$ の平均')
plt.title(r'サンプルサイズ $n$ と $\hat{\theta}$ の関係')
plt.legend()
plt.show()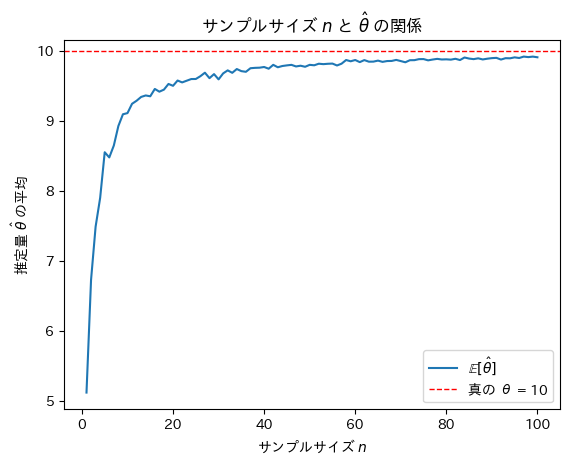
サンプルサイズnが増加するにつれて最尤推定量![]() は真のθに近づくことが確認できました。
は真のθに近づくことが確認できました。
2018 Q5(3)
一様分布の3つの順序統計量のうち第3と第1の確率変数の差の期待値と分散を求めました。
コード
同時確率密度関数f13(y1,y3)を視覚化してみます。またzが一定になる線も描画してみます。
# 2018 Q5(3) 2024.10.23
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 定義域 (y1 と y3 は [0, 1] の範囲で変動)
y1_values = np.linspace(0, 1, 100)
y3_values = np.linspace(0, 1, 100)
# メッシュグリッドを作成
Y1, Y3 = np.meshgrid(y1_values, y3_values)
# 同時確率密度関数 f13(y1, y3) = 6(y3 - y1), ただし y3 >= y1
f13 = np.where(Y3 >= Y1, 6 * (Y3 - Y1), 0)
# 等高線のための Z の値を設定 (例として Z = 0.2, 0.5, 0.8 を使用)
Z_values = [0.2, 0.5, 0.8]
# 3D グラフの描画を再度行う
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 3Dプロット (同時確率密度関数 f13(y1, y3))
ax.plot_surface(Y1, Y3, f13, cmap='viridis', alpha=0.8)
# 各 Z = Y3 - Y1 の線をプロット
for z_value in Z_values:
y1_line = np.linspace(0, 1 - z_value, 100)
y3_line = y1_line + z_value
ax.plot(y1_line, y3_line, zs=0, zdir='z', label=f'$Z = {z_value}$', lw=2)
# 軸ラベル
ax.set_title('同時確率密度関数 $f_{13}(y_1, y_3)$ と $Z = Y_3 - Y_1$', fontsize=14)
ax.set_xlabel('$y_1$', fontsize=12)
ax.set_ylabel('$y_3$', fontsize=12)
ax.set_zlabel('$f_{13}(y_1, y_3)$', fontsize=12)
# 凡例
ax.legend()
# グラフの表示
plt.show()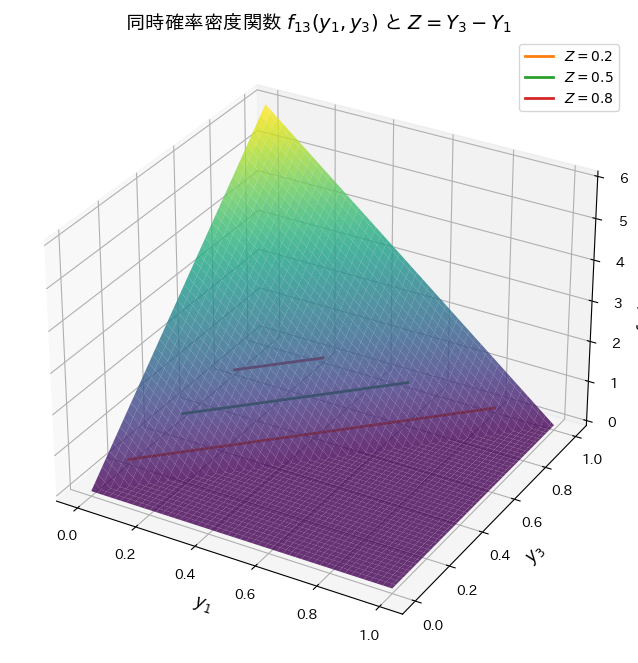
Z=z で垂直に切った断面の面積が![]() に相当します。
に相当します。
![]() を解いてZの確率密度関数を
を解いてZの確率密度関数を![]() のように求めます。順序統計量Y1とY3をシミュレーションし、理論と一致するか確認します。
のように求めます。順序統計量Y1とY3をシミュレーションし、理論と一致するか確認します。
# 2018 Q5(3) 2024.10.23
import numpy as np
import matplotlib.pyplot as plt
# サンプルデータの生成 (Z = Y3 - Y1 としてシミュレーション)
n_samples = 10000 # サンプル数
samples = np.random.uniform(0, 1, (n_samples, 3)) # 一様分布からサンプリング
Y1_samples = np.min(samples, axis=1) # 最小値 Y1
Y3_samples = np.max(samples, axis=1) # 最大値 Y3
# Z = Y3 - Y1 を計算
Z_samples = Y3_samples - Y1_samples
# Zの期待値と分散を計算
expected_Z = np.mean(Z_samples)
variance_Z = np.var(Z_samples)
# 理論値との比較
theoretical_Z_mean = 0.5
theoretical_Z_var = 1/20
# 期待値と分散を表示
print(f"シミュレーションによる E[Z](期待値): {expected_Z:.4f}, 理論値: {theoretical_Z_mean:.4f}")
print(f"シミュレーションによる Var[Z](分散): {variance_Z:.4f}, 理論値: {theoretical_Z_var:.4f}")
# Zの理論的な確率密度関数の定義
z_values = np.linspace(0, 1, 500)
f_z_theoretical = 6 * z_values * (1 - z_values)
# ヒストグラムと理論的なPDFを重ねて描画
plt.figure(figsize=(8, 6))
# サンプルのヒストグラムを描画 (確率密度として正規化)
plt.hist(Z_samples, bins=50, density=True, alpha=0.5, color='purple', label='Z samples (Y3 - Y1)')
# 理論的な確率密度関数のプロット
plt.plot(z_values, f_z_theoretical, label='Theoretical $f_Z(z) = 6z(1-z)$', color='black', linewidth=2)
# グラフの設定
plt.title('Z = Y3 - Y1 の確率密度関数 (シミュレーションと理論)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Z](期待値): 0.4992, 理論値: 0.5000
シミュレーションによる Var[Z](分散): 0.0500, 理論値: 0.0500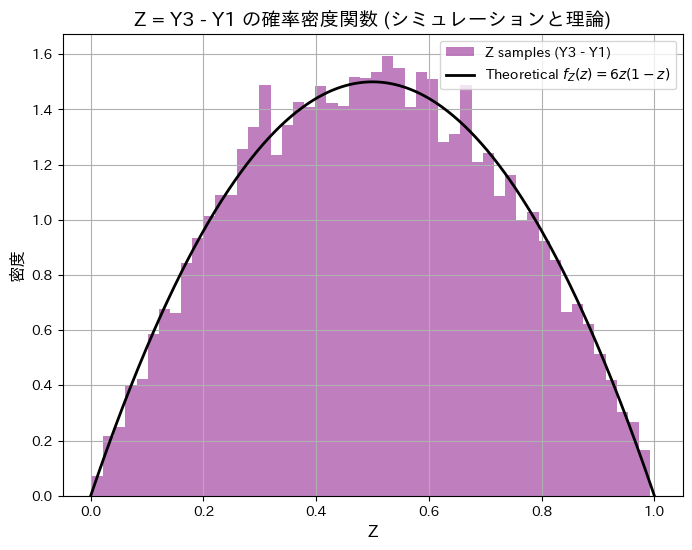
シミュレーションによる順序統計量Y3とY1の差の分布と期待値と分散が理論値と一致しました。
また興味深いことに、ZとY2は同じ分布になっていることが分かりました。
2018 Q5(2)
一様分布の3つの順序統計量のうち真ん中の確率密度関数と確率の計算をしました。
コード
シミュレーションにより順序統計量Y2の分布と期待値が理論値と一致するか確認します。
# 2018 Q5(2) 2024.10.22
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数 f2(y) の定義
f2_y = 6 * y_values * (1 - y_values)
# シミュレーションの設定
n_samples = 10000 # サンプル数
# 一様分布から3つの変数をサンプリング
samples = np.random.uniform(0, 1, (n_samples, 3))
# 順序統計量の第2要素を抽出 (Y2)
Y2_samples = np.median(samples, axis=1) # 中央値
# 期待値の計算
expected_Y2 = np.mean(Y2_samples)
# 理論値との比較
theoretical_Y2 = 0.5 # 中央値
# 期待値を表示
print(f"シミュレーションによる E[Y2](中間値の期待値): {expected_Y2:.4f}, 理論値: {theoretical_Y2:.4f}")
# ヒストグラムの作成
plt.figure(figsize=(8, 6))
# 理論密度関数 f2(y) のプロット
plt.plot(y_values, f2_y, label='$f_2(y) = 6y(1-y)$', color='red')
# サンプルのヒストグラムを追加 (確率密度として正規化)
plt.hist(Y2_samples, bins=50, density=True, alpha=0.5, color='red', label='Y2 samples (median)')
# グラフの設定
plt.title('確率密度関数 $f_2(y)$ とヒストグラム (シミュレーションと理論)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Y2](中間値の期待値): 0.5006, 理論値: 0.5000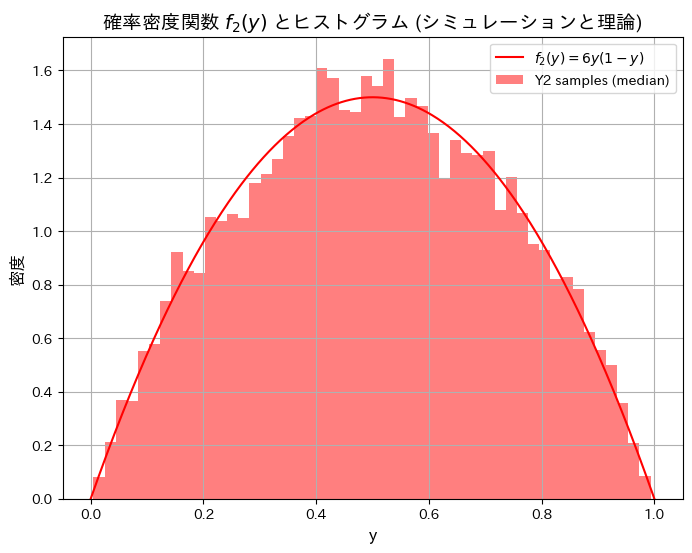
シミュレーションによる順序統計量Y1とY3の分布と期待値が理論値と一致しました。
次に、Y1~Y3の確率密度関数と累積分布関数を重ねて見てみます。
# 2018 Q5(2) 2024.10.22
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数の定義
f1_y = 3 * (1 - y_values) ** 2
f2_y = 6 * y_values * (1 - y_values)
f3_y = 3 * y_values ** 2
# CDF (累積分布関数) の計算
cdf1_y = np.cumsum(f1_y) * (y_values[1] - y_values[0])
cdf2_y = np.cumsum(f2_y) * (y_values[1] - y_values[0])
cdf3_y = np.cumsum(f3_y) * (y_values[1] - y_values[0])
# グラフの作成
plt.figure(figsize=(10, 8))
# 確率密度関数 (PDF) のプロット
plt.subplot(2, 1, 1)
plt.plot(y_values, f1_y, label='$f_1(y)$', color='blue')
plt.plot(y_values, f2_y, label='$f_2(y)$', color='red')
plt.plot(y_values, f3_y, label='$f_3(y)$', color='green')
plt.title('確率密度関数 (PDF)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# 累積分布関数 (CDF) のプロット
plt.subplot(2, 1, 2)
plt.plot(y_values, cdf1_y, label='$F_1(y)$', color='blue')
plt.plot(y_values, cdf2_y, label='$F_2(y)$', color='red')
plt.plot(y_values, cdf3_y, label='$F_3(y)$', color='green')
plt.title('累積分布関数 (CDF)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('累積確率', fontsize=12)
plt.legend(loc='lower right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()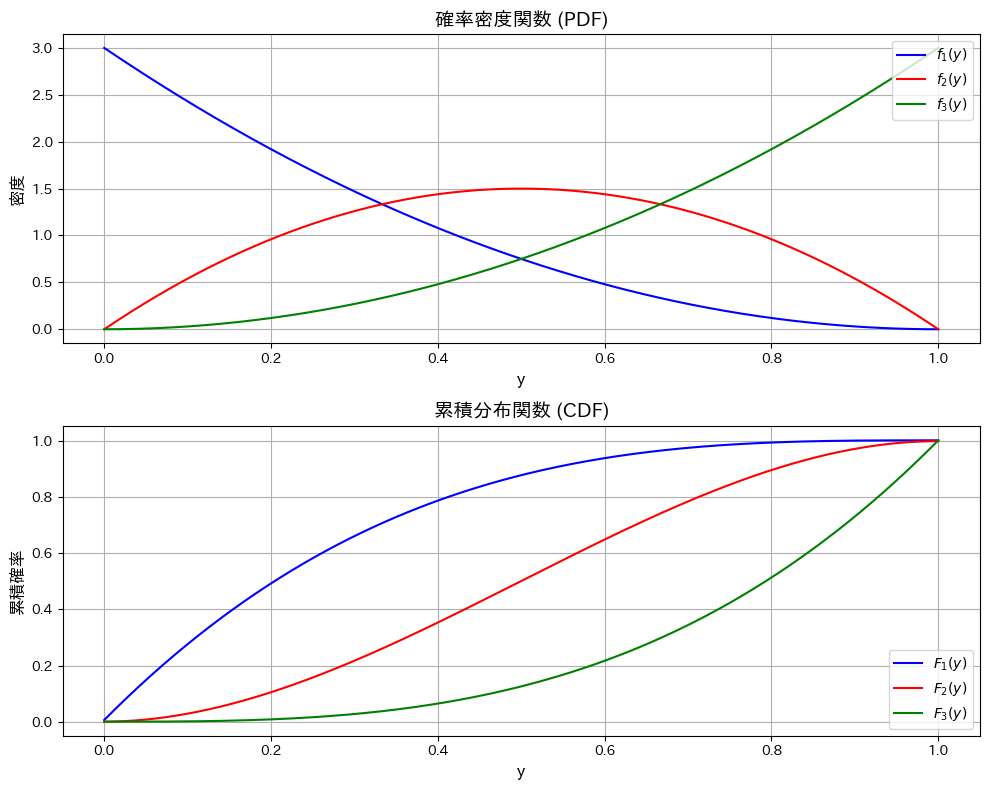
Y1は左寄り、Y2は中央寄り、Y3は右寄りになっていて、順序統計量の性質を直感的に表されています。Y2の確率密度関数は左右対称なので期待値が0.5になることも分かります。Y2の累積分布関数が直線でないことも面白いです。