2017 Q3(4)
標準化されたポアソン分布はパラメータλを∞に近づけると標準正規分布に収束することを示しました。
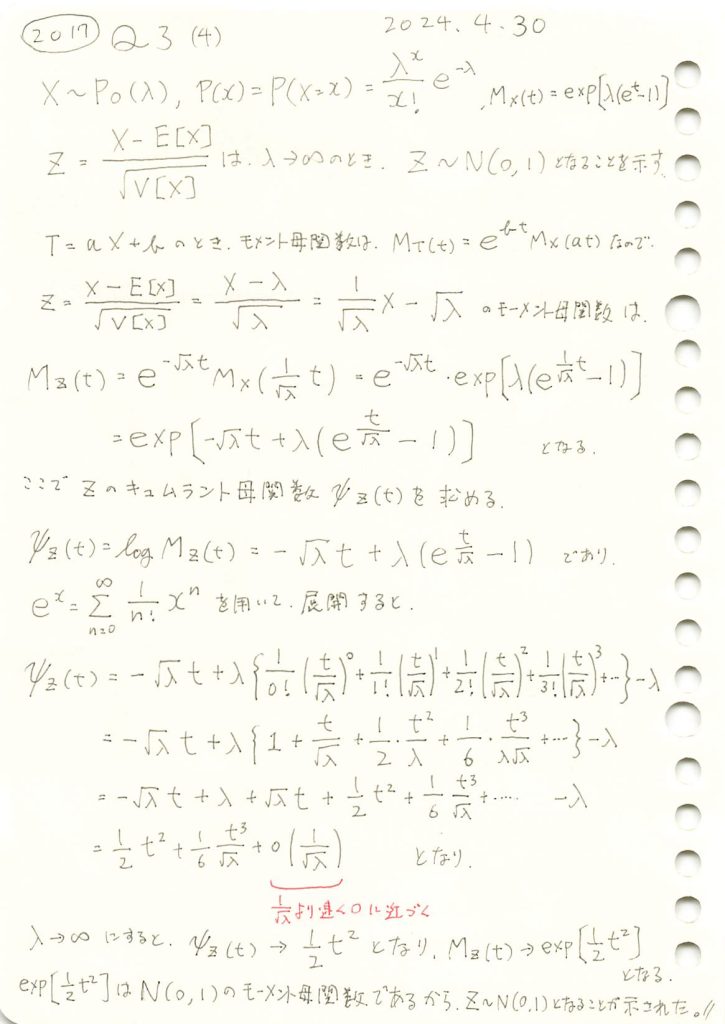
コード
λを変化させて標準化されたポアソン分布Zの分布をシミュレーションにより確認してみます。
# 2017 Q3(4) 2024.11.05
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# パラメータ設定
lambda_values = [10, 20, 50, 100]
sample_size = 10000 # サンプルサイズ
# 標準正規分布の理論値
z_values = np.linspace(-4, 4, 100)
normal_pdf = norm.pdf(z_values, 0, 1)
# 2x2 のグリッドでプロット
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.ravel()
# 各 λ に対してヒストグラムをプロット
for i, lambda_val in enumerate(lambda_values):
# ポアソン分布からサンプルを生成し、標準化
X_samples = np.random.poisson(lambda_val, sample_size)
Z_samples = (X_samples - lambda_val) / np.sqrt(lambda_val)
# 各 λ に対応するサブプロットでヒストグラムを描画
axes[i].hist(Z_samples, bins=100, density=True, alpha=0.5, color='orange', label=f"λ = {lambda_val}")
axes[i].plot(z_values, normal_pdf, color="red", linestyle="--", label="標準正規分布 N(0, 1)")
# グラフのカスタマイズ
axes[i].set_ylim(0, 1.8)
axes[i].set_xlabel("標準化変量 Z")
axes[i].set_ylabel("確率密度")
axes[i].set_title(f"標準化されたポアソン分布 (λ = {lambda_val})")
axes[i].legend()
axes[i].grid(True)
# レイアウト調整
plt.tight_layout()
plt.show()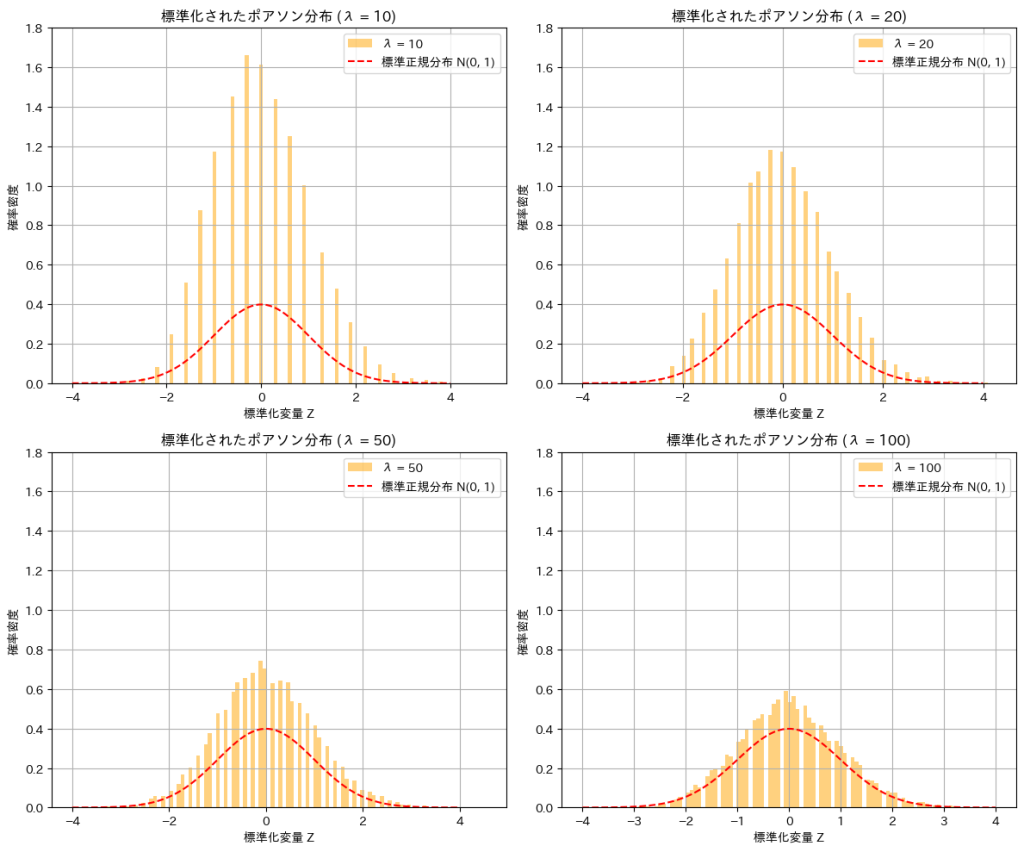
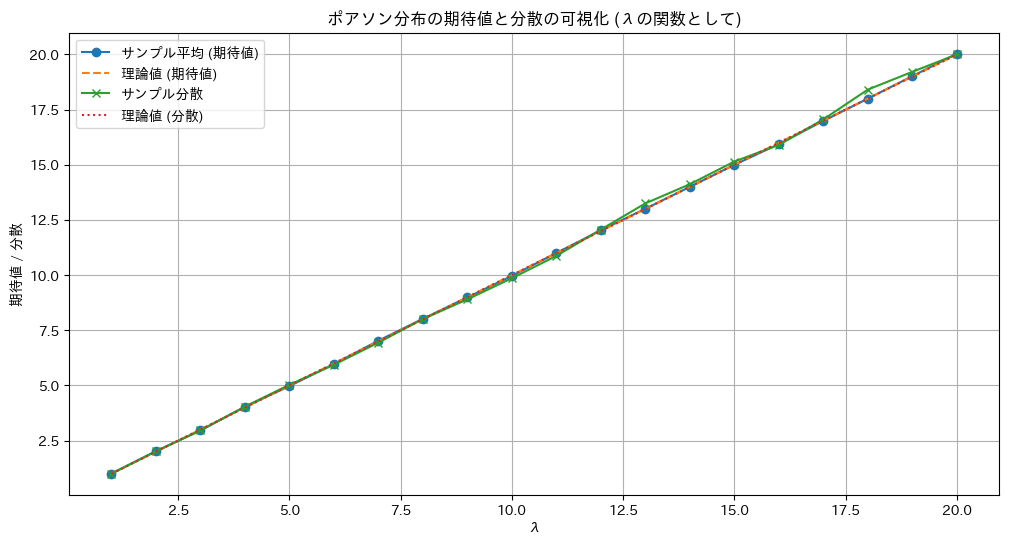
λ が増加するにつれて、標準化されたポアソン分布 Z の分布が標準正規分布に近づくことが確認できました。
2017 Q3(1)
二項分布の極限をとってポアソン分布を導出しました。
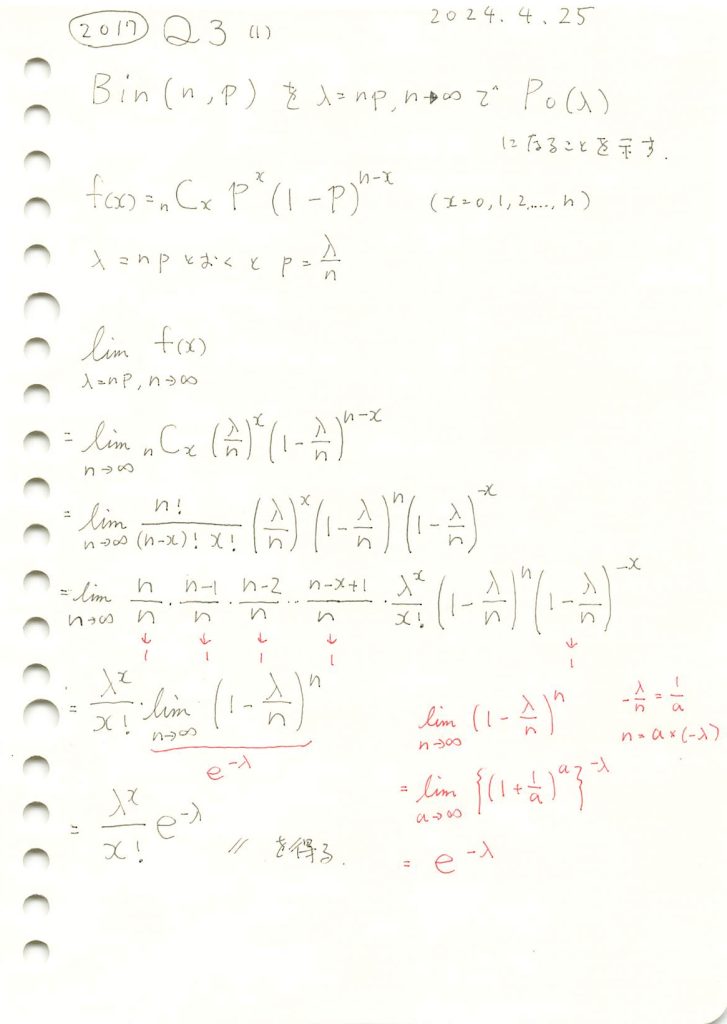
λ=5に固定しnを徐々に増加させて二項分布がポアソン分布に近づくのか確認してみます。
# 2017 Q3(1) 2024.11.2
import numpy as np
import matplotlib.pyplot as plt
# パラメータ
lambda_value = 5 # ポアソン分布の λ
n_values = [10, 50, 100, 500, 1000] # 二項分布の異なる n 値
sample_size = 10000 # サンプル数
# サブプロットの設定
fig, axes = plt.subplots(len(n_values), 1, figsize=(8, len(n_values) * 3))
fig.suptitle("二項分布の極限がポアソン分布に収束")
# 各 n に対するシミュレーションとプロット
for i, n in enumerate(n_values):
p = lambda_value / n # 与えられた λ に対する p の計算
binomial_samples = np.random.binomial(n, p, sample_size) # 二項分布のサンプル
poisson_samples = np.random.poisson(lambda_value, sample_size) # ポアソン分布のサンプル(比較用)
# ヒストグラムのプロット
axes[i].hist(binomial_samples, bins=range(0, 20), alpha=0.5, label=f"二項分布(n={n}, p={p:.3f})", density=True)
axes[i].hist(poisson_samples, bins=range(0, 20), alpha=0.5, label=f"ポアソン分布(λ={lambda_value})", density=True)
axes[i].legend()
axes[i].set_xlabel("x")
axes[i].set_ylabel("確率密度")
axes[i].set_title(f"n = {n}, p = {p:.5f}")
plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.show()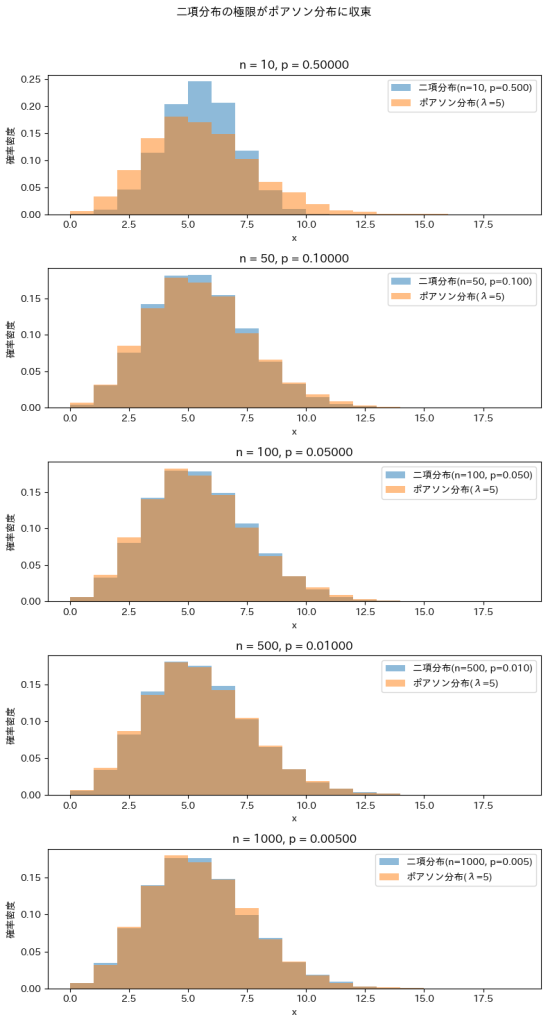
nが大きくなるにつれて二項分布はポアソン分布に近づくのが確認できました。
2021 Q3(1)
ポアソン分布のモーメント母関数を求めました。
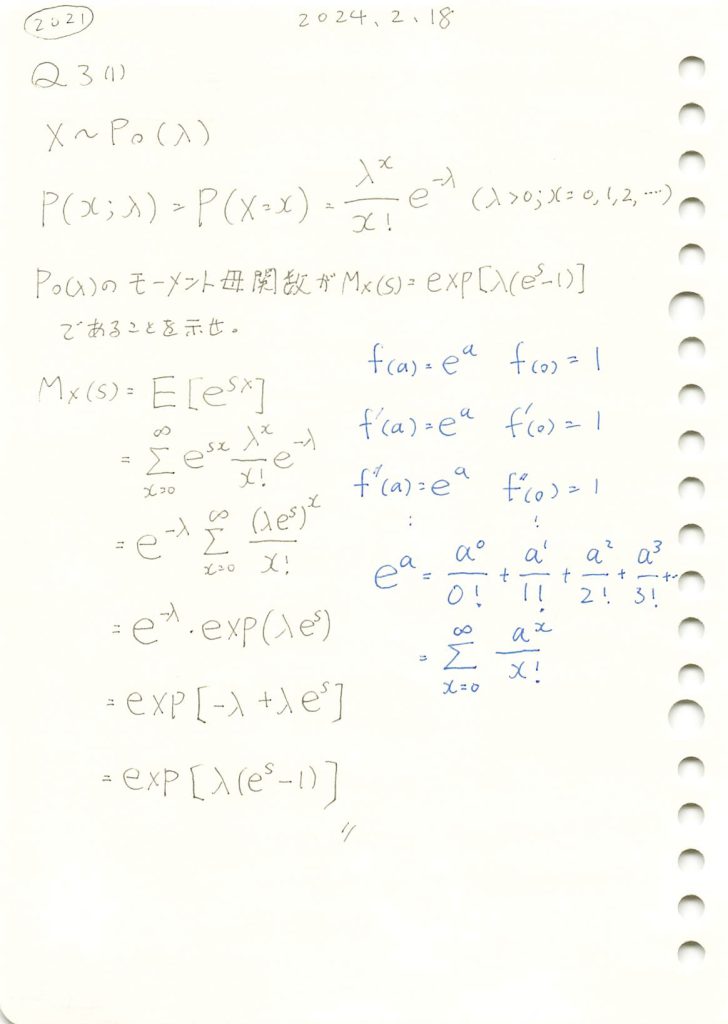
コード
数式を使った計算
# 2021 Q3(1) 2024.8.25
import sympy as sp
# 変数の定義
s, x, lambda_ = sp.symbols('s x lambda_', real=True, positive=True)
# ポアソン分布の確率質量関数 (PMF)
poisson_pmf = (lambda_**x * sp.exp(-lambda_)) / sp.factorial(x)
# モーメント母関数 M_X(s) の定義
M_X = sp.summation(sp.exp(s*x) * poisson_pmf, (x, 0, sp.oo))
# 結果を簡略化
M_X_simplified = sp.simplify(M_X)
# 結果を表示
M_X_simplified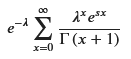
無限級数がe^xの形に変換されないようです。
exp(s) を t に置き換えて、最後に戻してみます。
# 2021 Q3(1) 2024.8.25
import sympy as sp
# 変数の定義
s, x, lambda_, t = sp.symbols('s x lambda_ t', real=True, positive=True)
# exp(s) を t に置き換え
summand = (lambda_ * t)**x / sp.factorial(x)
# モーメント母関数 M_X(s) の定義
M_X = sp.exp(-lambda_) * sp.summation(summand, (x, 0, sp.oo))
# 簡略化
M_X_simplified = sp.simplify(M_X)
# 最後に t を exp(s) に戻す
M_X_final = M_X_simplified.subs(t, sp.exp(s))
# 結果を表示
M_X_final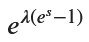
手計算と同じ形になりました。
モーメント母関数を使って期待値と分散を求めます。
import sympy as sp
# 変数の定義
s, lambda_ = sp.symbols('s lambda_', real=True, positive=True)
# モーメント母関数 M_X(s) の定義
M_X = sp.exp(lambda_ * (sp.exp(s) - 1))
# 1次モーメント(期待値)の計算
M_X_prime = sp.diff(M_X, s)
expectation = M_X_prime.subs(s, 0)
# 2次モーメントの計算
M_X_double_prime = sp.diff(M_X_prime, s)
second_moment = M_X_double_prime.subs(s, 0)
# 分散の計算
variance = second_moment - expectation**2
# 結果を表示
display(expectation, variance)
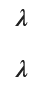
2022 Q3(5)
モーメント法によりガンマポアソン分布のパラメータの推定量を求めました。

コード
数式を使った計算
# 2022 Q3(5) 2024.8.6
from sympy import init_printing
from sympy import symbols, Eq, solve
# これでTexの表示ができる
init_printing()
# 変数の定義
r, p, X_bar, S_squared = symbols('r p X_bar S_squared')
alpha, beta = symbols('alpha beta')
# モーメント法の方程式を定義
# 期待値 E[X] にサンプル平均を一致させる
eq1_correct = Eq(X_bar, alpha / beta)
# 分散 V[X] にサンプル分散を一致させる
eq2_correct = Eq(S_squared, alpha / beta**2 + alpha / beta)
# 方程式を解いて α と β を求める
solutions_correct = solve((eq1_correct, eq2_correct), (alpha, beta))
solutions_correct
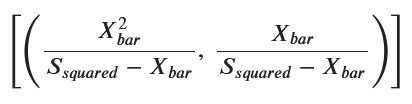
シミュレーションによる計算
# 2022 Q3(5) 2024.8.6
import numpy as np
from scipy.stats import nbinom
# 1. パラメータの設定
alpha_true = 3.0
beta_true = 2.0
# 2. 負の二項分布のパラメータ計算
r = alpha_true
p = beta_true / (beta_true + 1)
# 3. 負の二項分布から乱数を生成
sample_size = 10000
nbinom_samples = nbinom.rvs(r, p, size=sample_size)
# 4. サンプル統計量の計算
X_bar = np.mean(nbinom_samples)
S_squared = np.var(nbinom_samples, ddof=1)
# 5. モーメント法によるパラメータ推定
alpha_estimated = X_bar**2 / (S_squared - X_bar)
beta_estimated = X_bar / (S_squared - X_bar)
# 6. 推定結果の表示
print(f"推定された α: {alpha_estimated}")
print(f"推定された β: {beta_estimated}")
print(f"理論値 α: {alpha_true}")
print(f"理論値 β: {beta_true}")推定された α: 2.93536458612626
推定された β: 1.95157541794180
理論値 α: 3.0
理論値 β: 2.0アルゴリズム
シミュレーションによる計算
パラメータの設定:
- 真のパラメータ
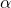 と
と 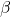 を設定する。
を設定する。
負の二項分布のパラメータ計算:
- パラメータ

- パラメータ
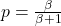
負の二項分布から乱数を生成:
- サンプルサイズ
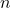 を設定し、負の二項分布から乱数を生成する。
を設定し、負の二項分布から乱数を生成する。
サンプル統計量の計算:
- サンプル平均
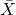 と分散
と分散 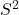 を計算する。
を計算する。
モーメント法によるパラメータ推定:
- 推定された
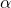 を
を 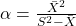 で計算する。
で計算する。 - 推定された
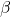 を
を 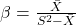 で計算する。
で計算する。
推定結果の表示:
- 推定された
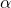 と
と 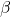 を表示する。
を表示する。 - 真の
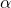 と
と 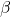 を表示する。
を表示する。
2022 Q3(4)
条件付き期待値の公式と条件付き分散の公式を使ってガンマポアソン分布の期待値と分散を求めました。

コード
数式を使った計算
# 2022 Q3(4) 2024.8.7
import sympy as sp
# 定義
k, lambda_var = sp.symbols('k lambda')
alpha, beta = sp.symbols('alpha beta', positive=True)
# ポアソン分布の確率質量関数
poisson_pmf = (lambda_var**k * sp.exp(-lambda_var)) / sp.factorial(k)
# ガンマ分布の確率密度関数
gamma_pdf = (beta**alpha / sp.gamma(alpha)) * lambda_var**(alpha - 1) * sp.exp(-beta * lambda_var)
# 周辺分布の計算
marginal_distribution = sp.integrate(poisson_pmf * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
# 期待値 E[X] の計算
expected_value = sp.summation(k * marginal_distribution, (k, 0, sp.oo)).simplify()
# 分散 V[X] の計算
expected_value_of_square = sp.summation(k**2 * marginal_distribution, (k, 0, sp.oo)).simplify()
variance = (expected_value_of_square - expected_value**2).simplify()
# 結果を表示
results = {
"期待値 E[X]": expected_value,
"分散 V[X]": variance
}
results{'期待値 E[X]': alpha/beta, '分散 V[X]': alpha*(beta + 1)/beta**2}シミュレーションによる計算
import numpy as np
# パラメータの設定
alpha = 3.0
beta = 2.0
sample_size = 10000
# ガンマ分布から λ を生成
lambda_samples = np.random.gamma(alpha, 1/beta, sample_size)
# 生成された λ を使ってポアソン分布から X を生成
poisson_samples = [np.random.poisson(lam) for lam in lambda_samples]
# サンプルの期待値と分散を計算
sample_mean = np.mean(poisson_samples)
sample_variance = np.var(poisson_samples)
# 理論値を計算
theoretical_mean = alpha / beta
theoretical_variance = alpha * (beta + 1) / beta**2
# 結果を表示
results_with_caption = {
"シミュレーションによる期待値": sample_mean,
"理論値による期待値": theoretical_mean,
"シミュレーションによる分散": sample_variance,
"理論値による分散": theoretical_variance
}
results_with_caption{'シミュレーションによる期待値': 1.5027,
'理論値による期待値': 1.5,
'シミュレーションによる分散': 2.31159271,
'理論値による分散': 2.25}2022 Q3(3)
ポアソン分布のパラメータλがガンマ分布に従うと負の二項分布になる。

コード
数式を使った計算
# 2022 Q3(3) 2024.8.5
import sympy as sp
# 定義
k = sp.symbols('k', integer=True)
alpha, beta = sp.symbols('alpha beta', positive=True)
lambda_var = sp.symbols('lambda', positive=True)
# ポアソン分布の確率質量関数
poisson_pmf = (lambda_var**k * sp.exp(-lambda_var)) / sp.factorial(k)
# ガンマ分布の確率密度関数
gamma_pdf = (beta**alpha / sp.gamma(alpha)) * lambda_var**(alpha - 1) * sp.exp(-beta * lambda_var)
# 周辺分布の計算
marginal_distribution = sp.integrate(poisson_pmf * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
marginal_distribution
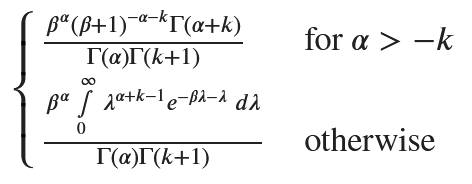
次式と同じなので、負の二項分布となる。
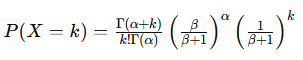
シミュレーションによる計算
# 2022 Q3(3) 2024.8.5
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma, nbinom
# パラメータの設定
alpha = 3.0
beta = 2.0
sample_size = 10000
# ガンマ分布から λ を生成
lambda_samples = np.random.gamma(alpha, 1/beta, sample_size)
# 生成された λ を使ってポアソン分布から X を生成
poisson_samples = [np.random.poisson(lam) for lam in lambda_samples]
# 負の二項分布のパラメータを設定
r = alpha
p = beta / (beta + 1)
# 負の二項分布から理論的な確率質量関数を計算
x = np.arange(0, max(poisson_samples) + 1)
nbinom_pmf = nbinom.pmf(x, r, p)
# ヒストグラムの描画
plt.hist(poisson_samples, bins=np.arange(0, max(poisson_samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black', rwidth=0.8)
# 理論的な負の二項分布の確率質量関数をプロット
plt.plot(x, nbinom_pmf, 'r', linestyle='-', label='理論的な負の二項分布')
# グラフのタイトルとラベル
plt.title('ポアソン-ガンマ混合分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()
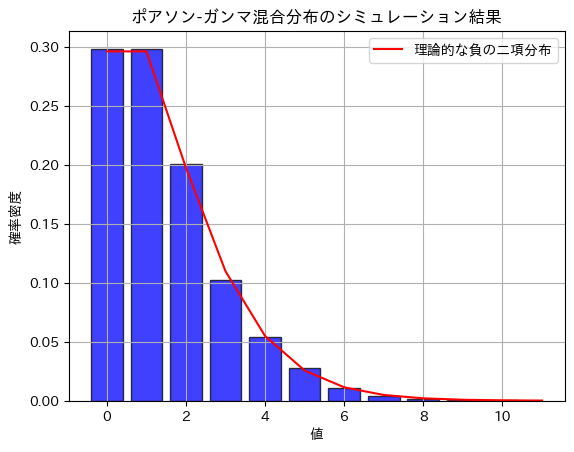
2022 Q3(2)
ガンマ分布の期待値と分散を求めました。
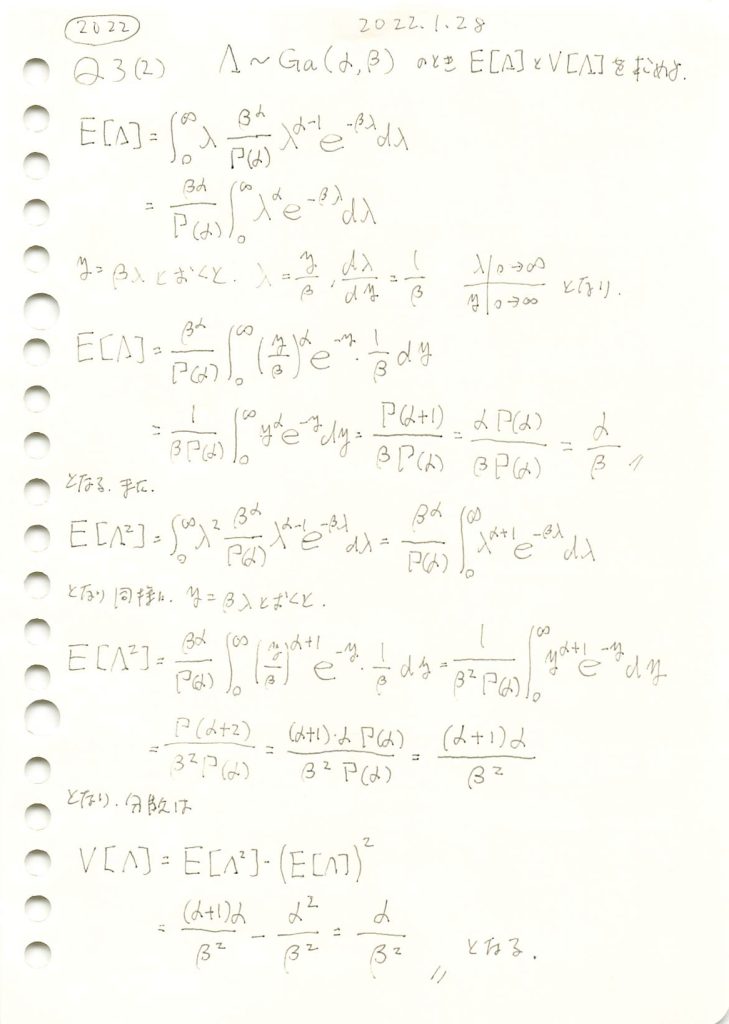
コード
数式を使った計算
## 2022 Q3(2) 2024.8.4
import sympy as sp
# 定義
lambda_var = sp.symbols('lambda')
alpha, beta = sp.symbols('alpha beta', positive=True)
# ガンマ分布の確率密度関数
gamma_pdf = (beta**alpha / sp.gamma(alpha)) * lambda_var**(alpha-1) * sp.exp(-beta * lambda_var)
# 期待値 E[Λ] の計算
expected_value = sp.integrate(lambda_var * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
# E[Λ^2] の計算
expected_value_Lambda2 = sp.integrate(lambda_var**2 * gamma_pdf, (lambda_var, 0, sp.oo)).simplify()
# 分散 V[Λ] の計算
variance = (expected_value_Lambda2 - expected_value**2).simplify()
# 結果を辞書形式で表示
{
"期待値 E[Λ]": expected_value,
"分散 V[Λ]": variance
}{'期待値 E[Λ]': alpha/beta, '分散 V[Λ]': alpha/beta**2}シミュレーションによる計算
## 2022 Q3(2) 2024.8.4
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ α と β の設定
alpha = 3.0
beta = 2.0
# サンプルサイズ
sample_size = 10000
# ガンマ分布に従う乱数を生成
samples = np.random.gamma(alpha, 1/beta, sample_size)
# 期待値と分散の計算
expected_value = np.mean(samples)
variance = np.var(samples)
# 結果の表示
print(f"期待値のシミュレーション結果: {expected_value}")
print(f"分散のシミュレーション結果: {variance}")
# ヒストグラムの描画
plt.hist(samples, bins=50, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なガンマ分布の確率密度関数をプロット
x = np.linspace(0, max(samples), 100)
gamma_pdf = gamma.pdf(x, alpha, scale=1/beta)
plt.plot(x, gamma_pdf, 'r', linestyle='-', label='理論的なガンマ分布')
# グラフのタイトルとラベル
plt.title('ガンマ分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()期待値のシミュレーション結果: 1.4947527551017439
分散のシミュレーション結果: 0.7452822182213243# パラメータ α と β の設定
alpha = 3.0
beta = 2.0
# 理論値の計算
theoretical_expected_value = alpha / beta
theoretical_variance = alpha / beta**2
# 結果の表示
print(f"理論値 - 期待値: {theoretical_expected_value}")
print(f"理論値 - 分散: {theoretical_variance}")理論値 - 期待値: 1.5
理論値 - 分散: 0.75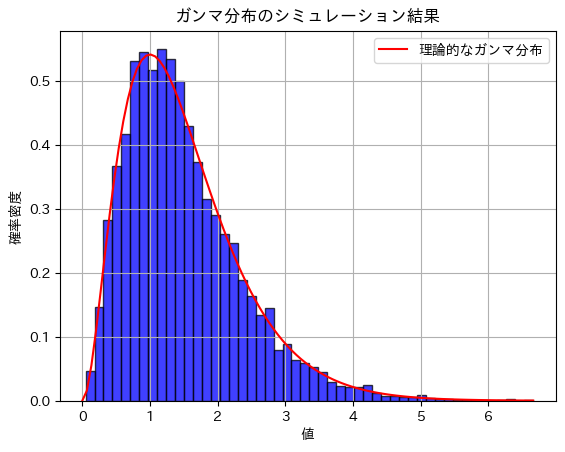
2022 Q3(1)
ポアソン分布の期待値と分散の導出。

コード
数式を使った計算
# 2022 Q3(1) 2024.8.3
import sympy as sp
# 定義
k = sp.symbols('k')
lambda_param = sp.symbols('lambda')
# ポアソン分布の確率関数
poisson_pmf = (lambda_param**k * sp.exp(-lambda_param)) / sp.factorial(k)
# 期待値 E[X] の計算
expected_value = sp.summation(k * poisson_pmf, (k, 0, sp.oo)).simplify()
# E[X^2] の計算
expected_value_X2 = sp.summation(k**2 * poisson_pmf, (k, 0, sp.oo)).simplify()
# 分散 V[X] の計算
variance = (expected_value_X2 - expected_value**2).simplify()
# 結果を表示
{
"期待値 E[X]": expected_value,
"分散 V[X]": variance
}{'期待値 E[X]': lambda, '分散 V[X]': lambda}シミュレーションによる計算
import numpy as np
# パラメータ λ の設定
lambda_param = 5
# シミュレーションの回数
num_simulations = 10000
# 各シミュレーションで生成するサンプルの数
sample_size = 1000
# シミュレーション結果の保存用
expected_values = []
variances = []
for _ in range(num_simulations):
# ポアソン分布に従う乱数を生成
samples = np.random.poisson(lambda_param, sample_size)
# 期待値を計算
expected_values.append(np.mean(samples))
# 分散を計算
variances.append(np.var(samples))
# シミュレーション結果の平均を計算
average_expected_value = np.mean(expected_values)
average_variance = np.mean(variances)
print(f"期待値のシミュレーション結果: {average_expected_value}")
print(f"分散のシミュレーション結果: {average_variance}")
期待値のシミュレーション結果: 4.999602
分散のシミュレーション結果: 4.9992533574プロット
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import factorial
# パラメータ λ の設定
lambda_param = 5
# サンプルサイズ
sample_size = 10000
# ポアソン分布に従う乱数を生成
samples = np.random.poisson(lambda_param, sample_size)
# ヒストグラムの描画
plt.hist(samples, bins=np.arange(0, max(samples) + 1) - 0.5, density=True, alpha=0.75, color='blue', edgecolor='black')
# 理論的なポアソン分布の確率質量関数をプロット
x = np.arange(0, max(samples) + 1)
poisson_pmf = (lambda_param**x * np.exp(-lambda_param)) / factorial(x)
plt.plot(x, poisson_pmf, 'r', marker='o', linestyle='-', label='理論的なポアソン分布')
# グラフのタイトルとラベル
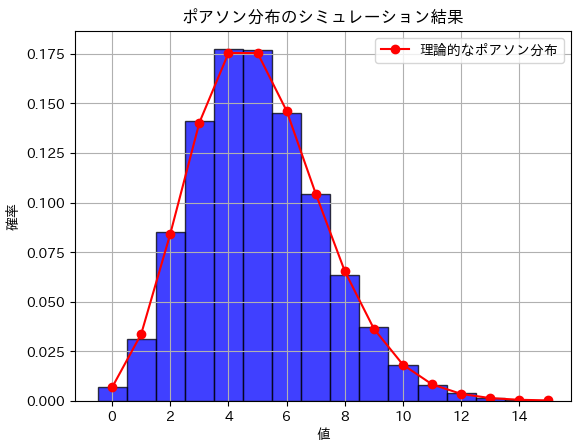
plt.title('ポアソン分布のシミュレーション結果')
plt.xlabel('値')
plt.ylabel('確率')
plt.legend()
# グラフの表示
plt.grid(True)
plt.show()