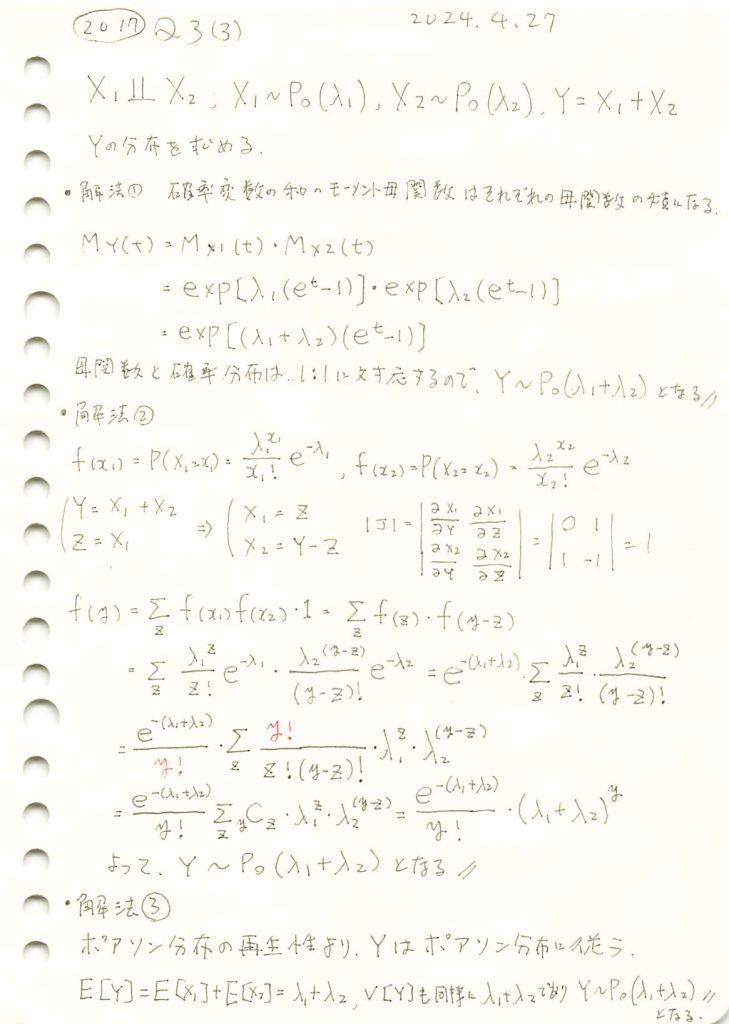ホーム » 分布 (ページ 4)
「分布」カテゴリーアーカイブ
2017 Q4(1)(2)(3)
線形関係のある確率変数との相関係数や条件付き確率分布を求めました。

コード
(1) Zが![]() に従うかシミュレーションし確かめます。
に従うかシミュレーションし確かめます。
# 2017 Q4(1) 2024.11.6
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 定数の設定
a = 1
k = 2
num_samples = 10000
# シミュレーション
X = np.random.normal(0, 1, num_samples)
Y = np.random.normal(0, 1, num_samples)
Z = a + k * X + Y
# 理論値の計算
mean_theory = a
std_dev_theory = np.sqrt(k**2 + 1)
# シミュレーションによる値の計算
mean_simulation = np.mean(Z)
std_dev_simulation = np.std(Z)
# 理論値とシミュレーションによる値の表示
print(f"理論上の期待値: {mean_theory}")
print(f"シミュレーションによる期待値: {mean_simulation}")
print(f"理論上の標準偏差: {std_dev_theory}")
print(f"シミュレーションによる標準偏差: {std_dev_simulation}")
# ヒストグラムのプロット
plt.hist(Z, bins=50, density=True, alpha=0.6, color='b', label="シミュレーションによる Z の分布")
# 理論分布のプロット
x_vals = np.linspace(min(Z), max(Z), 100)
plt.plot(x_vals, norm.pdf(x_vals, mean_theory, std_dev_theory), 'r', label="理論分布 N(a, k^2 + 1)")
# グラフのラベル
plt.title("Z の分布")
plt.xlabel("Z の値")
plt.ylabel("密度")
plt.legend()
plt.show()理論上の期待値: 1
シミュレーションによる期待値: 0.9814460670948696
理論上の標準偏差: 2.23606797749979
シミュレーションによる標準偏差: 2.2474915102454482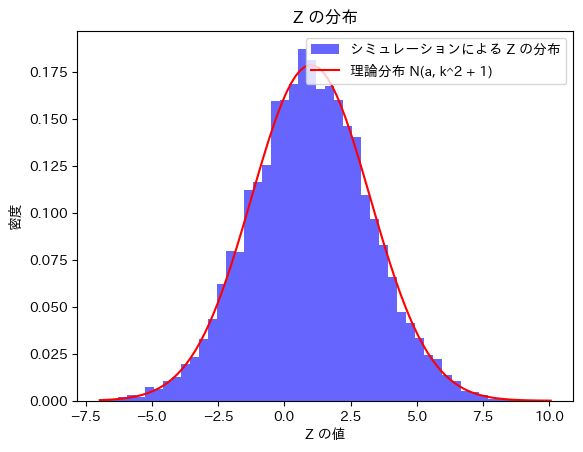
Zは![]() に従うことが確認できました。
に従うことが確認できました。
(2) 次に、XとZの相関係数をシミュレーションにより求めます。
# 2017 Q4(2) 2024.11.6
import numpy as np
import matplotlib.pyplot as plt
# 定数の設定
a = 1
k = 2
num_samples = 10000
# シミュレーション
X = np.random.normal(0, 1, num_samples)
Y = np.random.normal(0, 1, num_samples)
Z = a + k * X + Y
# 理論的な相関係数の計算
correlation_theory = k / np.sqrt(k**2 + 1)
# シミュレーションによる相関係数の計算
correlation_simulated = np.corrcoef(X, Z)[0, 1]
# 理論値とシミュレーションによる相関係数の表示
print(f"理論上の相関係数: {correlation_theory}")
print(f"シミュレーションによる相関係数: {correlation_simulated}")
# 相関係数の視覚化のための散布図のプロット
plt.figure(figsize=(8, 6))
plt.scatter(X, Z, alpha=0.5, s=10, label="X と Z の散布図")
plt.title("X と Z の相関関係")
plt.xlabel("X の値")
plt.ylabel("Z の値")
plt.legend()
plt.show()理論上の相関係数: 0.8944271909999159
シミュレーションによる相関係数: 0.8943931884333798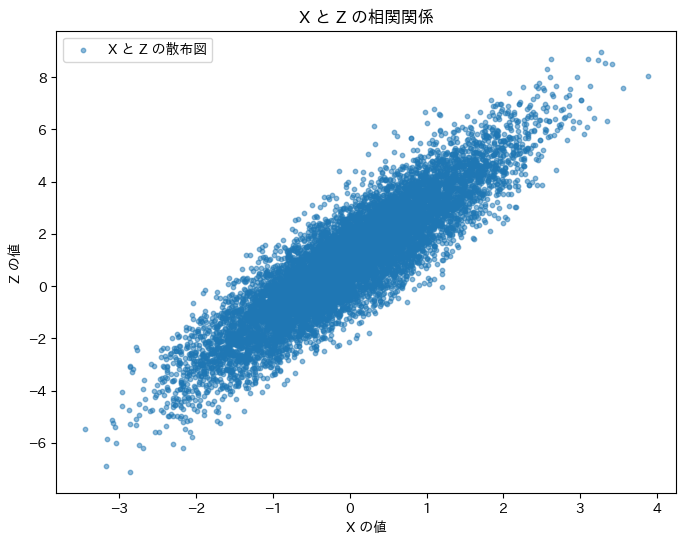
XとZの相関係数は理論値と一致しました。
(3) 次に、Z|X=xがN(a+kx,1)に従うかシミュレーションし確かめます。
# 2017 Q4(3) 2024.11.6
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 定数の設定
a = 1
k = 2
num_samples = 10000
x_fixed = 0.5 # 条件として与える X の値
# シミュレーション
Z_given_X = a + k * x_fixed + np.random.normal(0, 1, num_samples)
# 理論値の計算
mean_conditional = a + k * x_fixed
std_dev_conditional = 1 # 分散が 1 であるため
# シミュレーションによる値の計算
mean_simulation = np.mean(Z_given_X)
std_dev_simulation = np.std(Z_given_X)
# 理論値とシミュレーションによる値の表示
print(f"理論上の期待値 (Z | X = {x_fixed}): {mean_conditional}")
print(f"シミュレーションによる期待値: {mean_simulation}")
print(f"理論上の標準偏差: {std_dev_conditional}")
print(f"シミュレーションによる標準偏差: {std_dev_simulation}")
# 条件付き分布のヒストグラムのプロット
plt.hist(Z_given_X, bins=50, density=True, alpha=0.6, color='g', label=f"シミュレーションによる Z | X = {x_fixed} の分布")
# 理論分布のプロット
z_vals = np.linspace(min(Z_given_X), max(Z_given_X), 100)
plt.plot(z_vals, norm.pdf(z_vals, mean_conditional, std_dev_conditional), 'r', label="理論分布 N(a + kx, 1)")
# グラフの装飾
plt.title(f"条件付き分布 Z | X = {x_fixed}")
plt.xlabel("Z の値")
plt.ylabel("密度")
plt.legend()
plt.show()理論上の期待値 (Z | X = 0.5): 2.0
シミュレーションによる期待値: 1.978029240745398
理論上の標準偏差: 1
シミュレーションによる標準偏差: 1.0089203051741882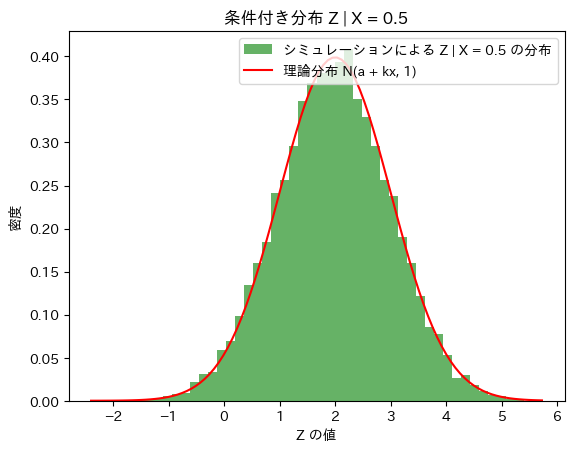
Z|X=xはN(a+kx,1)に従うことが確認できました。
2017 Q3(4)
標準化されたポアソン分布はパラメータλを∞に近づけると標準正規分布に収束することを示しました。
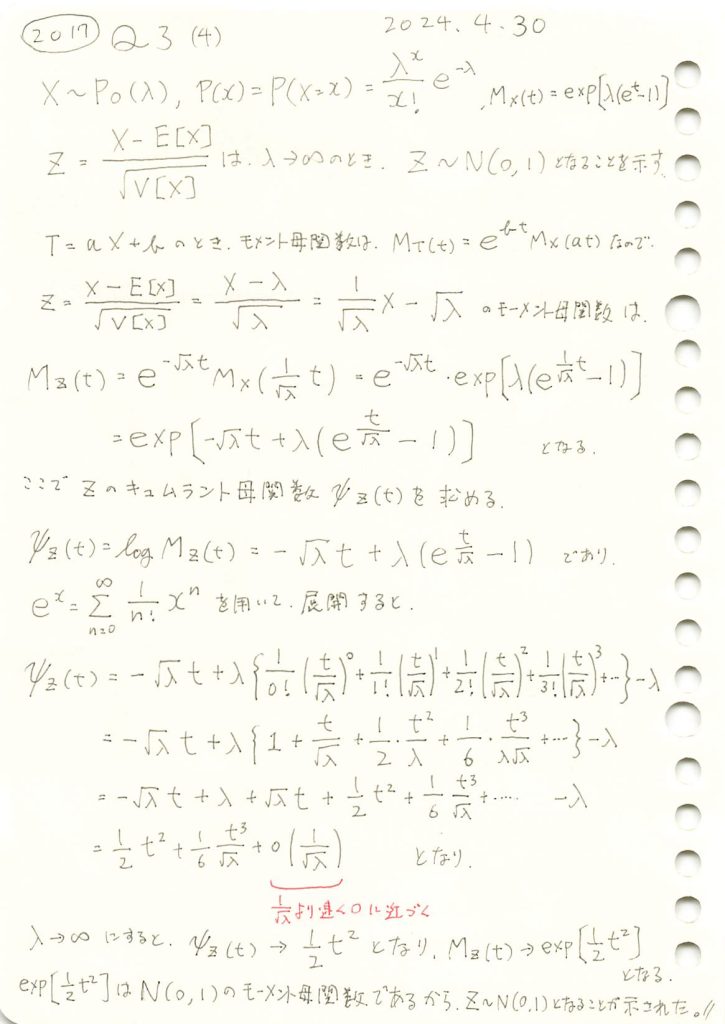
コード
λを変化させて標準化されたポアソン分布Zの分布をシミュレーションにより確認してみます。
# 2017 Q3(4) 2024.11.05
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# パラメータ設定
lambda_values = [10, 20, 50, 100]
sample_size = 10000 # サンプルサイズ
# 標準正規分布の理論値
z_values = np.linspace(-4, 4, 100)
normal_pdf = norm.pdf(z_values, 0, 1)
# 2x2 のグリッドでプロット
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.ravel()
# 各 λ に対してヒストグラムをプロット
for i, lambda_val in enumerate(lambda_values):
# ポアソン分布からサンプルを生成し、標準化
X_samples = np.random.poisson(lambda_val, sample_size)
Z_samples = (X_samples - lambda_val) / np.sqrt(lambda_val)
# 各 λ に対応するサブプロットでヒストグラムを描画
axes[i].hist(Z_samples, bins=100, density=True, alpha=0.5, color='orange', label=f"λ = {lambda_val}")
axes[i].plot(z_values, normal_pdf, color="red", linestyle="--", label="標準正規分布 N(0, 1)")
# グラフのカスタマイズ
axes[i].set_ylim(0, 1.8)
axes[i].set_xlabel("標準化変量 Z")
axes[i].set_ylabel("確率密度")
axes[i].set_title(f"標準化されたポアソン分布 (λ = {lambda_val})")
axes[i].legend()
axes[i].grid(True)
# レイアウト調整
plt.tight_layout()
plt.show()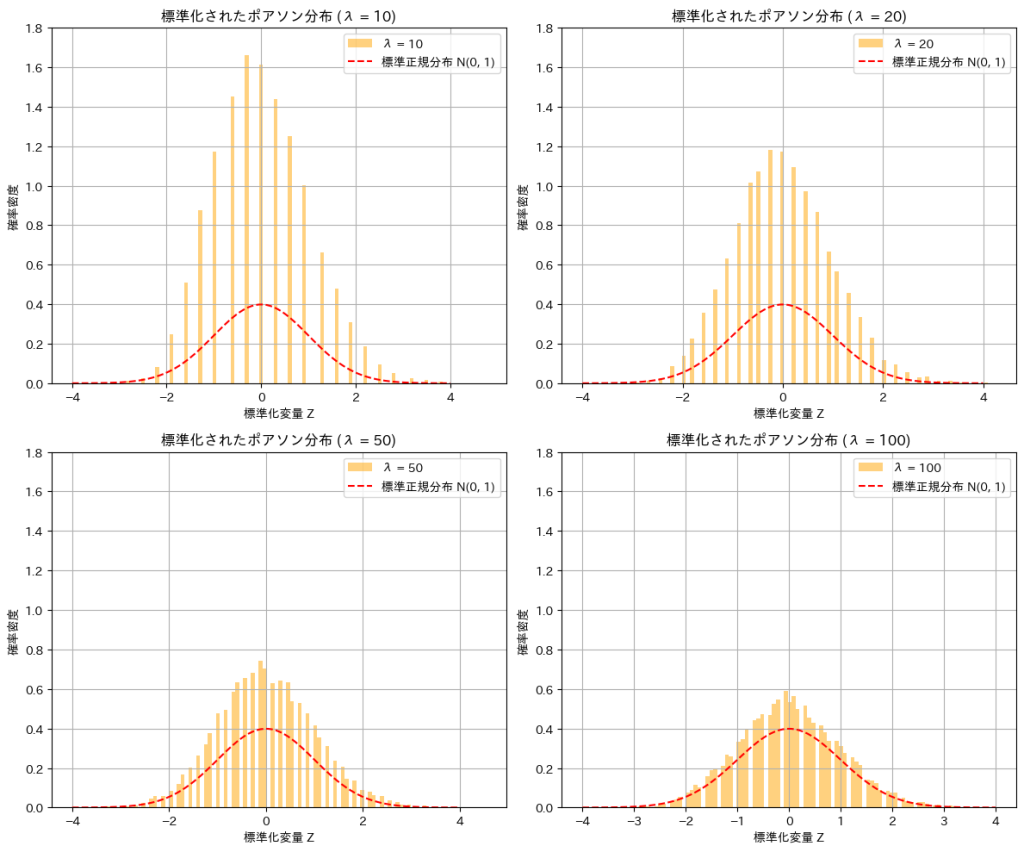
λ が増加するにつれて、標準化されたポアソン分布 Z の分布が標準正規分布に近づくことが確認できました。
2017 Q3(1)
二項分布の極限をとってポアソン分布を導出しました。
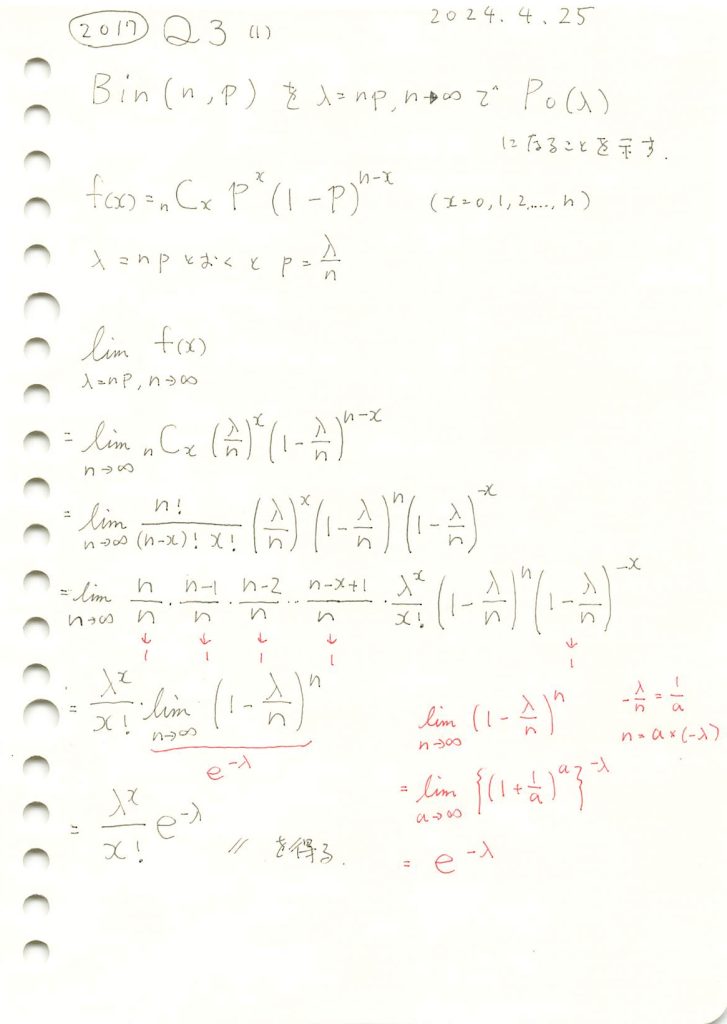
λ=5に固定しnを徐々に増加させて二項分布がポアソン分布に近づくのか確認してみます。
# 2017 Q3(1) 2024.11.2
import numpy as np
import matplotlib.pyplot as plt
# パラメータ
lambda_value = 5 # ポアソン分布の λ
n_values = [10, 50, 100, 500, 1000] # 二項分布の異なる n 値
sample_size = 10000 # サンプル数
# サブプロットの設定
fig, axes = plt.subplots(len(n_values), 1, figsize=(8, len(n_values) * 3))
fig.suptitle("二項分布の極限がポアソン分布に収束")
# 各 n に対するシミュレーションとプロット
for i, n in enumerate(n_values):
p = lambda_value / n # 与えられた λ に対する p の計算
binomial_samples = np.random.binomial(n, p, sample_size) # 二項分布のサンプル
poisson_samples = np.random.poisson(lambda_value, sample_size) # ポアソン分布のサンプル(比較用)
# ヒストグラムのプロット
axes[i].hist(binomial_samples, bins=range(0, 20), alpha=0.5, label=f"二項分布(n={n}, p={p:.3f})", density=True)
axes[i].hist(poisson_samples, bins=range(0, 20), alpha=0.5, label=f"ポアソン分布(λ={lambda_value})", density=True)
axes[i].legend()
axes[i].set_xlabel("x")
axes[i].set_ylabel("確率密度")
axes[i].set_title(f"n = {n}, p = {p:.5f}")
plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.show()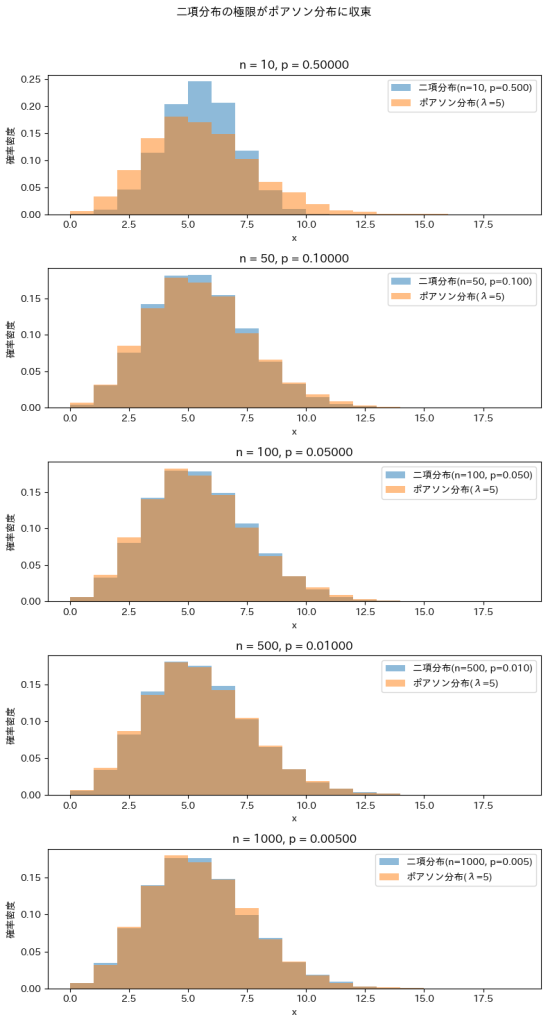
nが大きくなるにつれて二項分布はポアソン分布に近づくのが確認できました。
2017 Q2(4)
二つの不偏推定量の分散の大きさを比較する事でどちらの推定量が望ましいかを調べました。

コード
θ=10,n=20としてシミュレーションを行い、θ’とθ’’の分布を重ねて描画してみます。
# 2017 Q2(4) 2024.11.1
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
n = 20 # サンプルサイズ
num_trials = 1000 # シミュレーションの試行回数
# θ' = 2 * X̄ と θ'' = (n + 1) / n * X_max の推定値を記録するリスト
theta_prime_estimates = []
theta_double_prime_estimates = []
# シミュレーションを実行
for _ in range(num_trials):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# θ' = 2 * X̄ を計算
theta_prime = 2 * np.mean(samples)
theta_prime_estimates.append(theta_prime)
# θ'' = (n + 1) / n * X_max を計算
theta_double_prime = (n + 1) / n * np.max(samples)
theta_double_prime_estimates.append(theta_double_prime)
# ヒストグラムの表示
plt.hist(theta_prime_estimates, bins=30, edgecolor='black', density=True, alpha=0.5, label=r'$\theta\' = 2 \bar{X}$')
plt.hist(theta_double_prime_estimates, bins=30, edgecolor='black', density=True, alpha=0.5, label=r'$\theta\'\' = \frac{n + 1}{n} X_{\max}$')
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel('推定量')
plt.ylabel('密度')
plt.title(r'$\theta\' = 2 \bar{X}$ と $\theta\'\' = \frac{n + 1}{n} X_{\max}$ の分布')
plt.legend()
plt.show()
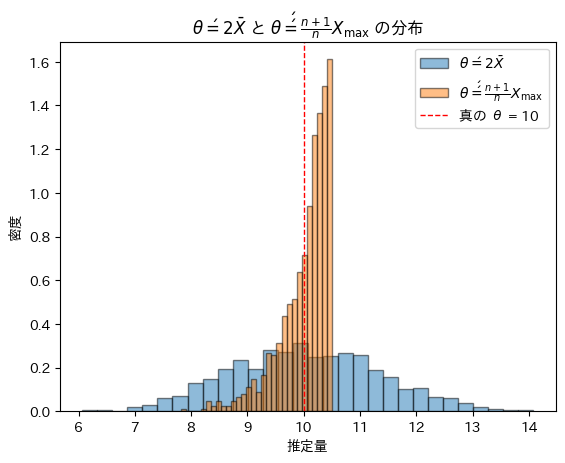
θ’とθ’’は同じ期待(θ)を持つものの横の広がり方が異なりθ’’の分散はθ’の分散よりも小さいことが確認できました。
次にサンプルサイズnを変化させて不偏推定量θ’とθ’’を重ねて描画してみます。
# 2017 Q2(4) 2024.11.1
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
max_n = 100 # 最大サンプルサイズ
num_trials_per_n = 100 # 各サンプルサイズでの試行回数
# 各サンプルサイズにおける θ' と θ'' の平均を記録
theta_prime_means = []
theta_double_prime_means = []
# サンプルサイズ n を 1 から max_n まで増やしながらシミュレーション
for n in range(1, max_n + 1):
theta_prime_estimates = []
theta_double_prime_estimates = []
for _ in range(num_trials_per_n):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# θ' = 2 * X̄ を計算し、その推定値を記録
theta_prime = 2 * np.mean(samples)
theta_prime_estimates.append(theta_prime)
# θ'' = (n + 1) / n * X_max を計算し、その推定値を記録
theta_double_prime = (n + 1) / n * np.max(samples)
theta_double_prime_estimates.append(theta_double_prime)
# 各 n に対する θ' と θ'' の平均を保存
theta_prime_means.append(np.mean(theta_prime_estimates))
theta_double_prime_means.append(np.mean(theta_double_prime_estimates))
# グラフ描画
plt.plot(range(1, max_n + 1), theta_prime_means, label=r'$\mathbb{E}[\theta\']$', color='orange', alpha=0.7)
plt.plot(range(1, max_n + 1), theta_double_prime_means, label=r'$\mathbb{E}[\theta\'\']$', color='saddlebrown', alpha=0.7)
plt.axhline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'サンプルサイズ $n$')
plt.ylabel('推定量の平均')
plt.title(r'サンプルサイズ $n$ と 推定量 $\theta\' = 2 \bar{X}$, $\theta\'\' = \frac{n + 1}{n} X_{\max}$ の関係')
plt.legend()
plt.show()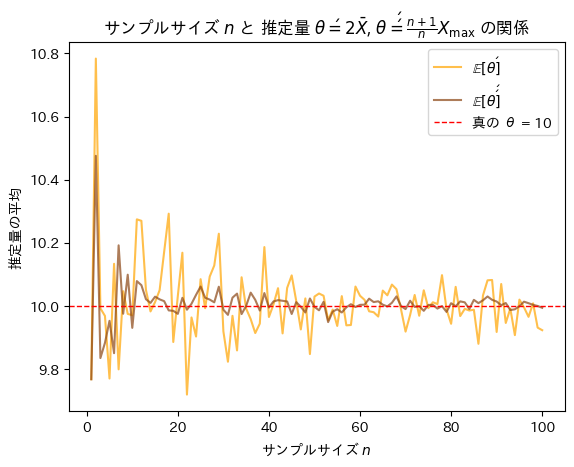
サンプルサイズnが増加するにつれて不偏推定量θ’とθ’’は共に真のθに近づくものの振幅が異なりθ’’の分散はθ’の分散よりも小さいことが確認できました。また収束する速度もθ’’はθ’よりも速いことが確認できました。
2017 Q2(3)
サンプルデータの最大値の(n+1)/n倍が一様分布の上限値の不偏推定量であることの証明をしました。
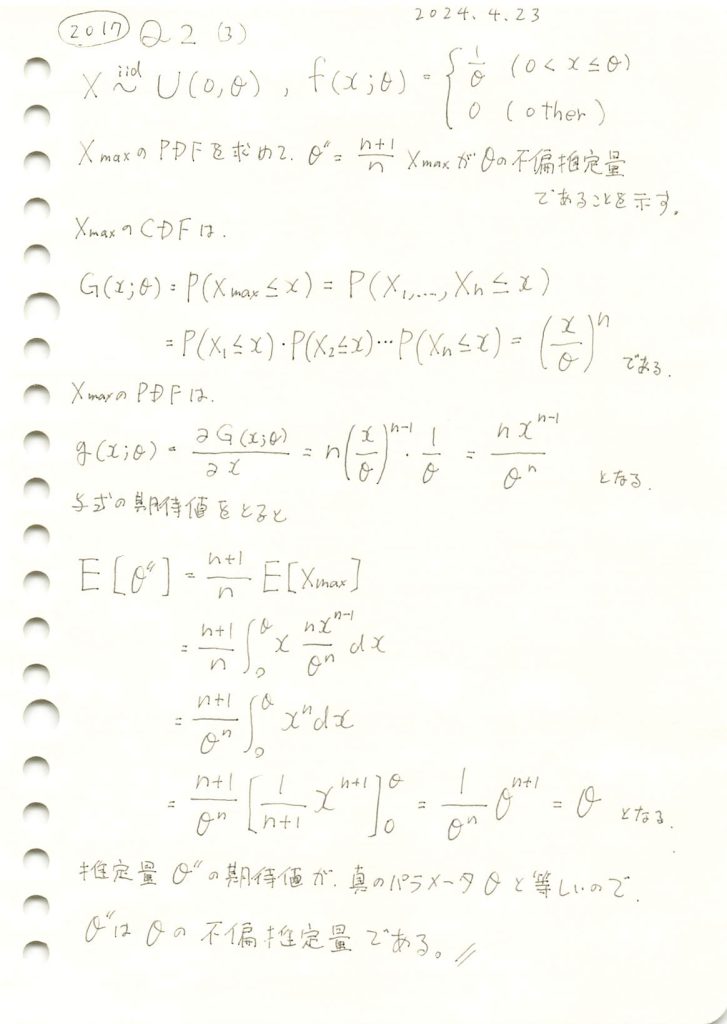
コード
θ=10,n=20としてシミュレーションを行い、θ’’の分布を見てみます。
# 2017 Q2(3) 2024.10.31
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
n = 20 # サンプルサイズ
num_trials = 1000 # シミュレーションの試行回数
# シミュレーションを実行
theta_double_prime_estimates = []
for _ in range(num_trials):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプルの最大値 X_max を計算し、それを用いて θ'' を計算
theta_double_prime = (n + 1) / n * np.max(samples)
theta_double_prime_estimates.append(theta_double_prime)
# θ'' の分布をヒストグラムで表示
plt.hist(theta_double_prime_estimates, bins=30, edgecolor='black', density=True)
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'$\theta\'\' = \frac{n + 1}{n} X_{\max}$')
plt.ylabel('密度')
plt.title(r'$\theta\'\' = \frac{n + 1}{n} X_{\max}$ の分布')
plt.legend()
plt.show()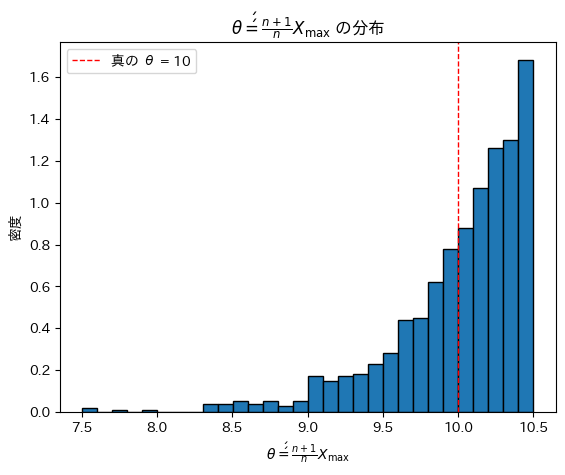
θ’’は、元となるXmaxの分布を右にずらした形状を取っています。期待値は真のθに一致しているようです。
次にサンプルサイズnを変化させて不偏推定量θ’’がどうなるのか確認をします。
# 2017 Q2(3) 2024.10.31
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
max_n = 100 # 最大サンプルサイズ
num_trials_per_n = 100 # 各サンプルサイズでの試行回数
# 各サンプルサイズにおける θ'' の平均を記録
theta_double_prime_means = []
# サンプルサイズ n を 1 から max_n まで増やしながらシミュレーション
for n in range(1, max_n + 1):
theta_double_prime_estimates = []
for _ in range(num_trials_per_n):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプルの最大値 X_max を計算し、それを用いて θ'' を計算
theta_double_prime = (n + 1) / n * np.max(samples)
theta_double_prime_estimates.append(theta_double_prime)
# 各 n に対する θ'' の平均を保存
theta_double_prime_means.append(np.mean(theta_double_prime_estimates))
# グラフ描画
plt.plot(range(1, max_n + 1), theta_double_prime_means, label=r'$\mathbb{E}[\theta\'\']$')
plt.axhline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'サンプルサイズ $n$')
plt.ylabel(r'推定量 $\theta\'\' = \frac{n + 1}{n} X_{\max}$ の平均')
plt.title(r'サンプルサイズ $n$ と $\theta\'\' = \frac{n + 1}{n} X_{\max}$ の関係')
plt.legend()
plt.show()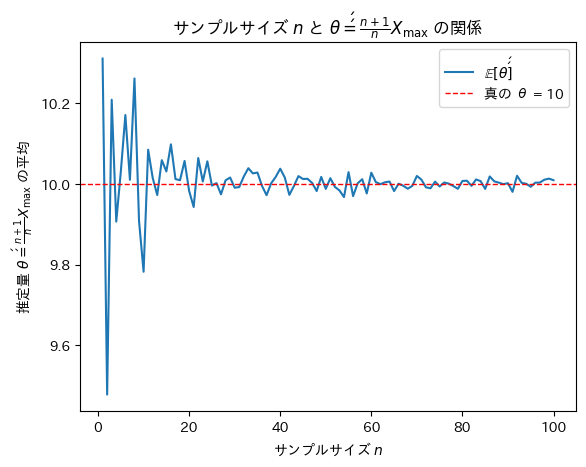
サンプルサイズnが増加するにつれて不偏推定量θ’’は真のθに近づくことが確認できました。
2017 Q2(2)
標本平均の2倍が一様分布の上限値の不偏推定量であることの証明をしました。

コード
θ=10,n=20としてシミュレーションを行い、θ’の分布を見てみます。
# 2017 Q2(2) 2024.10.30
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
theta_true = 10 # 真の θ の値
n = 20 # 1試行あたりのサンプル数
num_trials = 1000 # シミュレーションの試行回数
# シミュレーションを実行
theta_prime_estimates = []
for _ in range(num_trials):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプル平均 X̄ を計算し、それを用いて θ' を計算
theta_prime = 2 * np.mean(samples)
theta_prime_estimates.append(theta_prime)
# θ' の分布をヒストグラムで表示
plt.hist(theta_prime_estimates, bins=30, edgecolor='black', density=True)
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'$\theta\' = 2\bar{X}$')
plt.ylabel('密度')
plt.title(r'$\theta\' = 2\bar{X}$ の分布')
plt.legend()
plt.show()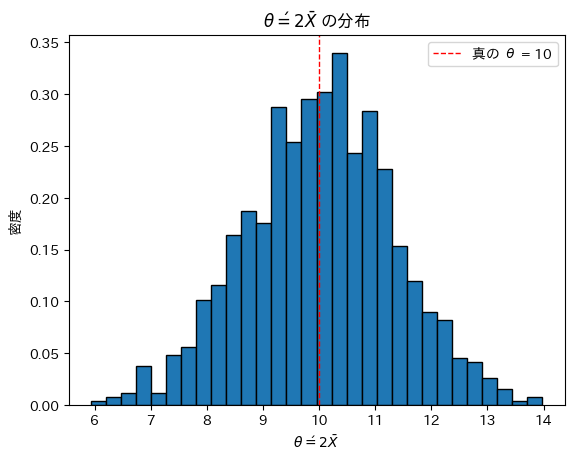
θ’は真のθを中心に左右対称にバラついています。θ’は不偏であるように見えます。
次にサンプルサイズnを変化させて不偏推定量θ’がどうなるのか確認をします。
# 2017 Q2(2) 2024.10.30
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
max_n = 100 # 最大サンプルサイズ
num_trials_per_n = 100 # 各サンプルサイズでの試行回数
# 各サンプルサイズにおける θ' の平均を記録
theta_prime_means = []
# サンプルサイズ n を 1 から max_n まで増やしながらシミュレーション
for n in range(1, max_n + 1):
theta_prime_estimates = []
for _ in range(num_trials_per_n):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプル平均 X̄ を計算し、それを用いて θ' を計算
theta_prime = 2 * np.mean(samples)
theta_prime_estimates.append(theta_prime)
# 各 n に対する θ' の平均を保存
theta_prime_means.append(np.mean(theta_prime_estimates))
# グラフ描画
plt.plot(range(1, max_n + 1), theta_prime_means, label=r'$\mathbb{E}[\theta\']$')
plt.axhline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'サンプルサイズ $n$')
plt.ylabel(r'推定量 $\theta\' = 2 \bar{X}$ の平均')
plt.title(r'サンプルサイズ $n$ と $\theta\' = 2 \bar{X}$ の関係')
plt.legend()
plt.show()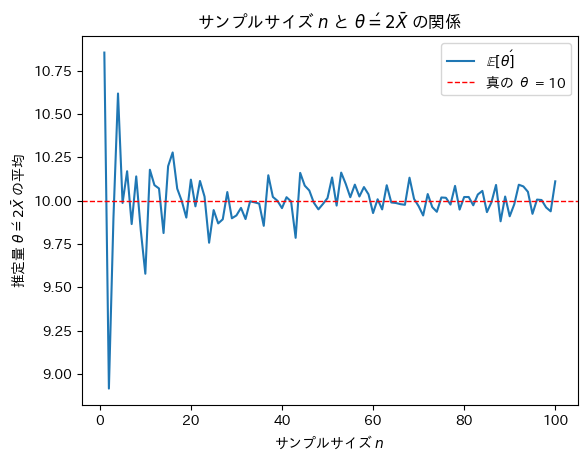
サンプルサイズnが増加するにつれて不偏推定量θ’は真のθに近づくことが確認できました。
2017 Q2(1)
一様分布の上限の最尤推定量を求めました。

コード
θ=10,n=20としてシミュレーションを行い、![]() の分布を見てみます。
の分布を見てみます。
# 2017 Q2(1) 2024.10.29
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
theta_true = 10 # 真の θ の値
n = 20 # 1試行あたりのサンプル数
num_trials = 1000 # シミュレーションの試行回数
# シミュレーションを実行
theta_estimates = []
for _ in range(num_trials):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプルの最大値を推定値 θ_hat として記録
theta_hat = np.max(samples)
theta_estimates.append(theta_hat)
# 推定値の分布をヒストグラムで表示
plt.hist(theta_estimates, bins=30, edgecolor='black', density=True)
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'$\hat{\theta}$')
plt.ylabel('密度')
plt.title(r'$\hat{\theta} = X_{\max}$ の分布')
plt.legend()
plt.show()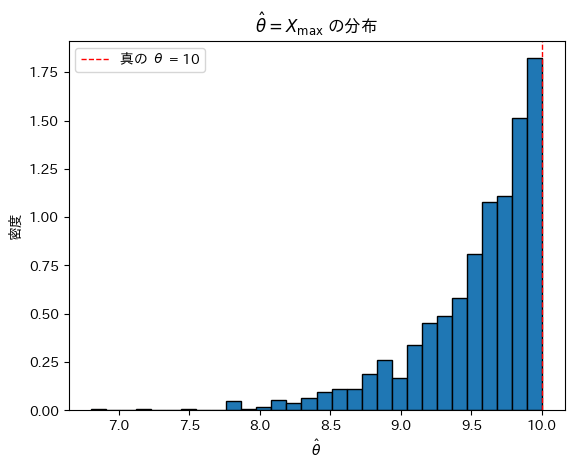
![]() は真のθより大きくならないため、結果としてθよりやや小さな値を取っているように見えます。
は真のθより大きくならないため、結果としてθよりやや小さな値を取っているように見えます。
次にサンプルサイズnを変化させて最尤推定量![]() がどうなるのか確認をします。
がどうなるのか確認をします。
# 2017 Q2(1) 2024.10.29
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
max_n = 100 # 最大サンプルサイズ
num_trials_per_n = 100 # 各サンプルサイズでの試行回数
# 各サンプルサイズにおける θ^ の平均を記録
theta_hat_means = []
# サンプルサイズ n を 1 から max_n まで増やしながらシミュレーション
for n in range(1, max_n + 1):
theta_estimates = []
for _ in range(num_trials_per_n):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプルの最大値を推定値 θ_hat として記録
theta_hat = np.max(samples)
theta_estimates.append(theta_hat)
# 各 n に対する θ^ の平均を保存
theta_hat_means.append(np.mean(theta_estimates))
# グラフ描画
plt.plot(range(1, max_n + 1), theta_hat_means, label=r'$\mathbb{E}[\hat{\theta}]$')
plt.axhline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'サンプルサイズ $n$')
plt.ylabel(r'推定量 $\hat{\theta}$ の平均')
plt.title(r'サンプルサイズ $n$ と $\hat{\theta}$ の関係')
plt.legend()
plt.show()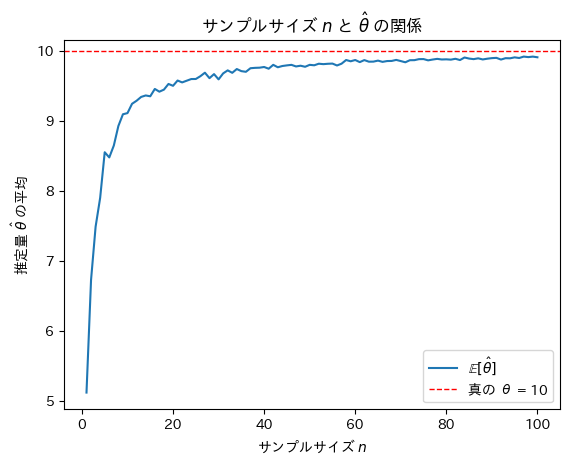
サンプルサイズnが増加するにつれて最尤推定量![]() は真のθに近づくことが確認できました。
は真のθに近づくことが確認できました。
2018 Q5(3)
一様分布の3つの順序統計量のうち第3と第1の確率変数の差の期待値と分散を求めました。
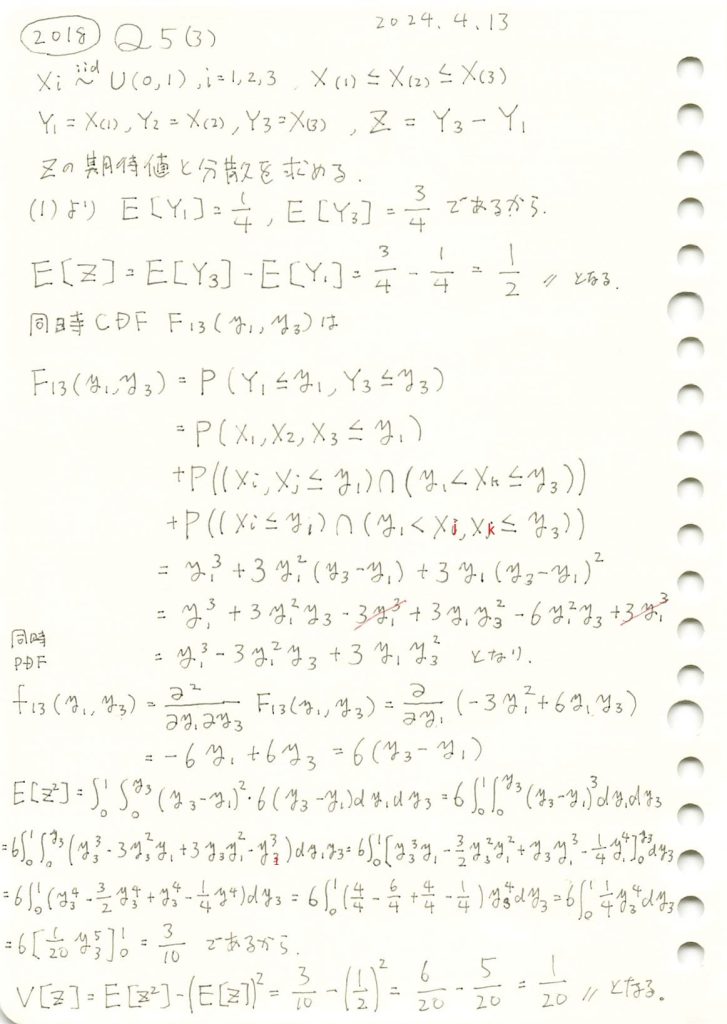
コード
同時確率密度関数f13(y1,y3)を視覚化してみます。またzが一定になる線も描画してみます。
# 2018 Q5(3) 2024.10.23
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 定義域 (y1 と y3 は [0, 1] の範囲で変動)
y1_values = np.linspace(0, 1, 100)
y3_values = np.linspace(0, 1, 100)
# メッシュグリッドを作成
Y1, Y3 = np.meshgrid(y1_values, y3_values)
# 同時確率密度関数 f13(y1, y3) = 6(y3 - y1), ただし y3 >= y1
f13 = np.where(Y3 >= Y1, 6 * (Y3 - Y1), 0)
# 等高線のための Z の値を設定 (例として Z = 0.2, 0.5, 0.8 を使用)
Z_values = [0.2, 0.5, 0.8]
# 3D グラフの描画を再度行う
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 3Dプロット (同時確率密度関数 f13(y1, y3))
ax.plot_surface(Y1, Y3, f13, cmap='viridis', alpha=0.8)
# 各 Z = Y3 - Y1 の線をプロット
for z_value in Z_values:
y1_line = np.linspace(0, 1 - z_value, 100)
y3_line = y1_line + z_value
ax.plot(y1_line, y3_line, zs=0, zdir='z', label=f'$Z = {z_value}$', lw=2)
# 軸ラベル
ax.set_title('同時確率密度関数 $f_{13}(y_1, y_3)$ と $Z = Y_3 - Y_1$', fontsize=14)
ax.set_xlabel('$y_1$', fontsize=12)
ax.set_ylabel('$y_3$', fontsize=12)
ax.set_zlabel('$f_{13}(y_1, y_3)$', fontsize=12)
# 凡例
ax.legend()
# グラフの表示
plt.show()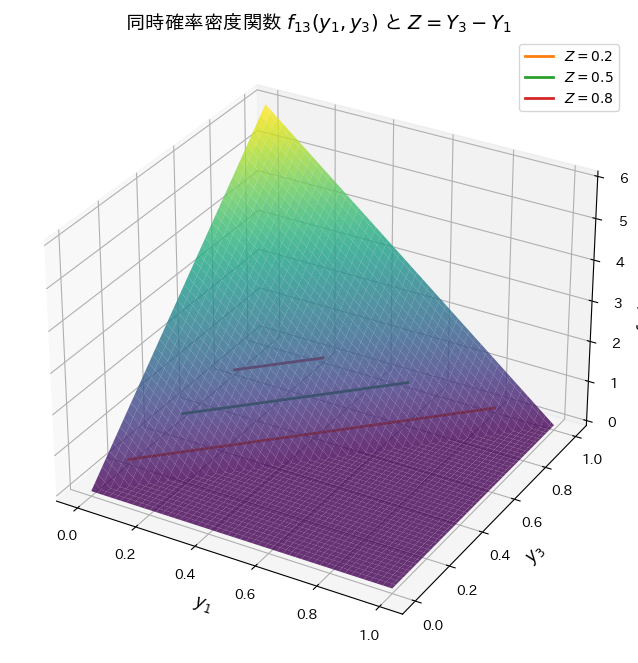
Z=z で垂直に切った断面の面積が![]() に相当します。
に相当します。
![]() を解いてZの確率密度関数を
を解いてZの確率密度関数を![]() のように求めます。順序統計量Y1とY3をシミュレーションし、理論と一致するか確認します。
のように求めます。順序統計量Y1とY3をシミュレーションし、理論と一致するか確認します。
# 2018 Q5(3) 2024.10.23
import numpy as np
import matplotlib.pyplot as plt
# サンプルデータの生成 (Z = Y3 - Y1 としてシミュレーション)
n_samples = 10000 # サンプル数
samples = np.random.uniform(0, 1, (n_samples, 3)) # 一様分布からサンプリング
Y1_samples = np.min(samples, axis=1) # 最小値 Y1
Y3_samples = np.max(samples, axis=1) # 最大値 Y3
# Z = Y3 - Y1 を計算
Z_samples = Y3_samples - Y1_samples
# Zの期待値と分散を計算
expected_Z = np.mean(Z_samples)
variance_Z = np.var(Z_samples)
# 理論値との比較
theoretical_Z_mean = 0.5
theoretical_Z_var = 1/20
# 期待値と分散を表示
print(f"シミュレーションによる E[Z](期待値): {expected_Z:.4f}, 理論値: {theoretical_Z_mean:.4f}")
print(f"シミュレーションによる Var[Z](分散): {variance_Z:.4f}, 理論値: {theoretical_Z_var:.4f}")
# Zの理論的な確率密度関数の定義
z_values = np.linspace(0, 1, 500)
f_z_theoretical = 6 * z_values * (1 - z_values)
# ヒストグラムと理論的なPDFを重ねて描画
plt.figure(figsize=(8, 6))
# サンプルのヒストグラムを描画 (確率密度として正規化)
plt.hist(Z_samples, bins=50, density=True, alpha=0.5, color='purple', label='Z samples (Y3 - Y1)')
# 理論的な確率密度関数のプロット
plt.plot(z_values, f_z_theoretical, label='Theoretical $f_Z(z) = 6z(1-z)$', color='black', linewidth=2)
# グラフの設定
plt.title('Z = Y3 - Y1 の確率密度関数 (シミュレーションと理論)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Z](期待値): 0.4992, 理論値: 0.5000
シミュレーションによる Var[Z](分散): 0.0500, 理論値: 0.0500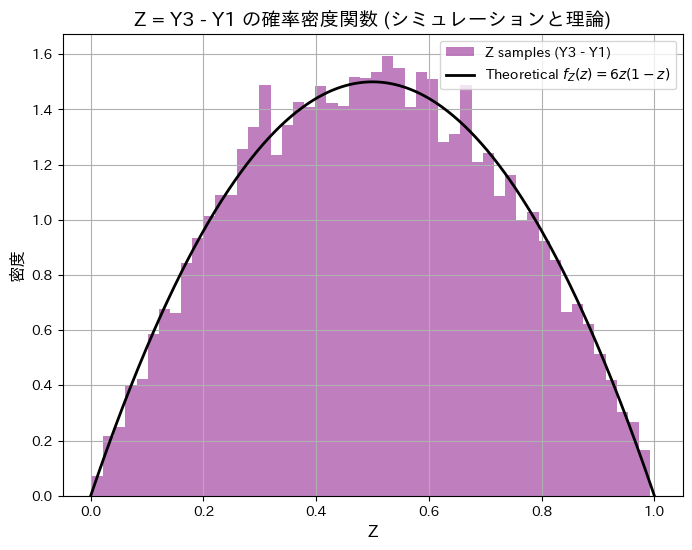
シミュレーションによる順序統計量Y3とY1の差の分布と期待値と分散が理論値と一致しました。
また興味深いことに、ZとY2は同じ分布になっていることが分かりました。