ホーム » 分布 (ページ 2)
「分布」カテゴリーアーカイブ
2014 Q1(3)
一様分布の指数を取るn個の確率変数のうち特定の一つが最大値をとる確率を求めました。
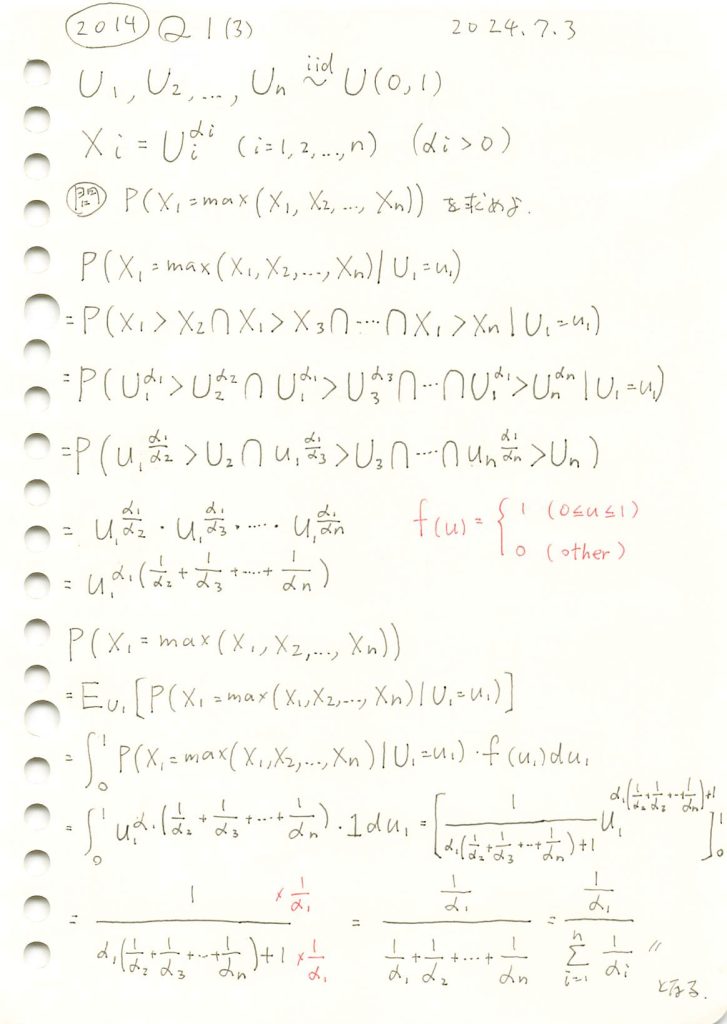
コード
与式は![]() と考え、
と考え、![]() とした場合の
とした場合の![]() をシミュレーションで計算し、理論値と比較します。
をシミュレーションで計算し、理論値と比較します。
# 2014 Q1(3) 2024.12.30
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
n_simulations = 10**6
# 確率変数の数とパラメータの設定
n = 5
alphas = [2, 3, 4, 5, 6] # α1, α2, ..., αn
# 一様分布からサンプリング
U = np.random.uniform(0, 1, (n_simulations, n))
X = U**np.array(alphas)
# 確率変数 Z を計算 (Z = X1 - max(X2, ..., Xn))
Z_diff = X[:, 0] - np.max(X[:, 1:], axis=1)
# Z の累積分布関数 (CDF) を計算
z_sorted = np.sort(Z_diff)
cdf_Z = np.arange(1, len(z_sorted) + 1) / len(z_sorted)
# Z = 0 の累積確率を計算
cumulative_prob_at_zero = cdf_Z[np.searchsorted(z_sorted, 0)]
# 理論値の計算
theoretical_prob = (1 / alphas[0]) / sum(1 / alpha for alpha in alphas)
# 結果を出力
print(f"Z = 0 における続繁確率: {cumulative_prob_at_zero:.3f}")
print(f"シミュレーション結果: P(X1 > max(X2, ..., Xn)) = {1 - cumulative_prob_at_zero:.6f}")
print(f"理論値: P(X1 > max(X2, ..., Xn)) = {theoretical_prob:.6f}")
print(f"誤差: {abs((1 - cumulative_prob_at_zero) - theoretical_prob):.6f}")
# PDF および CDF のプロット (PDF にも Z = 0 の赤い線を追加)
plt.figure(figsize=(14, 6))
# PDF
plt.subplot(1, 2, 1)
plt.hist(Z_diff, bins=100, density=True, alpha=0.7, label=r'$Z = X_1 - \max(X_2, ..., X_n)$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)') # Z = 0 の赤い線を追加
plt.title('Z = X1 - max(X2, ..., Xn) の確率密度関数 (PDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()
# CDF
plt.subplot(1, 2, 2)
plt.plot(z_sorted, cdf_Z, label=r'$Z = X_1 - \max(X_2, ..., X_n)$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)') # Z = 0 の赤い線
plt.text(0.05, cumulative_prob_at_zero, f'{cumulative_prob_at_zero:.3f}', color='red', fontsize=12)
plt.title('Z = X1 - max(X2, ..., Xn) の続繁分布関数 (CDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('続繁確率', fontsize=12)
plt.legend()
plt.tight_layout()
plt.show()Z = 0 における続繁確率: 0.655
シミュレーション結果: P(X1 > max(X2, ..., Xn)) = 0.345030
理論値: P(X1 > max(X2, ..., Xn)) = 0.344828
誤差: 0.000202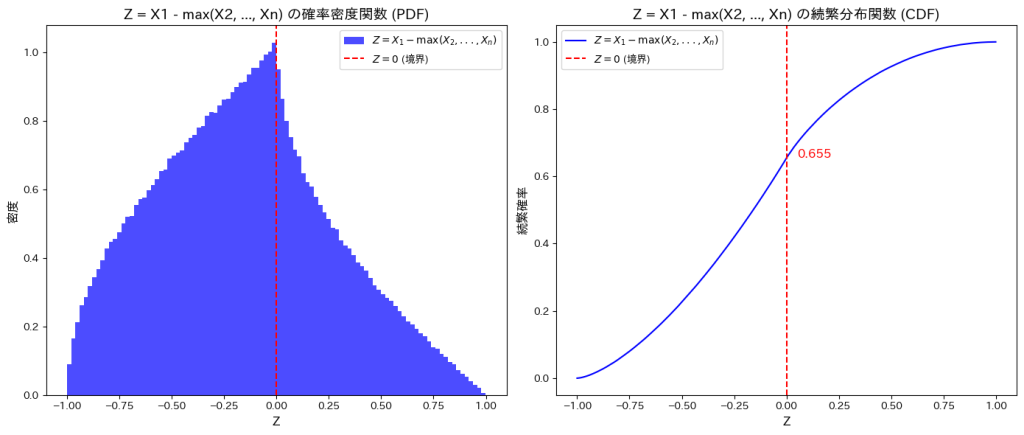
![]() はシミュレーションの結果、理論値と一致しました。
はシミュレーションの結果、理論値と一致しました。
2014 Q1(2)
一様分布の指数を取る三つの確率変数のうち特定の一つが最大値をとる確率を求めました。

コード
与式は![]() と考え、
と考え、![]() とした場合の
とした場合の![]() をシミュレーションで計算し、理論値と比較します。
をシミュレーションで計算し、理論値と比較します。
# 2014 Q1(2) 2024.12.29
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
n_simulations = 10**6
# 一様分布からサンプリング
U = np.random.uniform(0, 1, n_simulations)
V = np.random.uniform(0, 1, n_simulations)
W = np.random.uniform(0, 1, n_simulations)
# パラメータの設定
alpha, beta, gamma = 2, 3, 4
# X, Y, Z の計算
X = U**alpha
Y = V**beta
Z = W**gamma
# 確率変数 Z を計算 (例: Z = X - max(Y, Z))
Z_diff = X - np.maximum(Y, Z)
# Z の累積分布関数 (CDF) を計算
z_sorted = np.sort(Z_diff)
cdf_Z = np.arange(1, len(z_sorted) + 1) / len(z_sorted)
# Z = 0 の累積確率を計算
cumulative_prob_at_zero = cdf_Z[np.searchsorted(z_sorted, 0)]
# 理論値の計算
theoretical_prob = (1 / alpha) / (1 / alpha + 1 / beta + 1 / gamma)
# 結果を出力
print(f"Z = 0 における累積確率: {cumulative_prob_at_zero:.3f}")
print(f"シミュレーション結果: P(X > max(Y, Z)) = {1 - cumulative_prob_at_zero:.6f}")
print(f"理論値: P(X > max(Y, Z)) = {theoretical_prob:.6f}")
print(f"誤差: {abs((1 - cumulative_prob_at_zero) - theoretical_prob):.6f}")
# PDF および CDF のプロット (PDF にも Z = 0 の赤い線を追加)
plt.figure(figsize=(14, 6))
# PDF
plt.subplot(1, 2, 1)
plt.hist(Z_diff, bins=100, density=True, alpha=0.7, label=r'$Z = X - \max(Y, Z)$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)') # Z = 0 の赤い線を追加
plt.title('Z = X - max(Y, Z) の確率密度関数 (PDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()
# CDF
plt.subplot(1, 2, 2)
plt.plot(z_sorted, cdf_Z, label=r'$Z = X - \max(Y, Z)$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)') # Z = 0 の赤い線
plt.text(0.05, cumulative_prob_at_zero, f'{cumulative_prob_at_zero:.3f}', color='red', fontsize=12)
plt.title('Z = X - max(Y, Z) の累積分布関数 (CDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('累積確率', fontsize=12)
plt.legend()
plt.tight_layout()
plt.show()Z = 0 における累積確率: 0.538
シミュレーション結果: P(X > max(Y, Z)) = 0.462111
理論値: P(X > max(Y, Z)) = 0.461538
誤差: 0.000573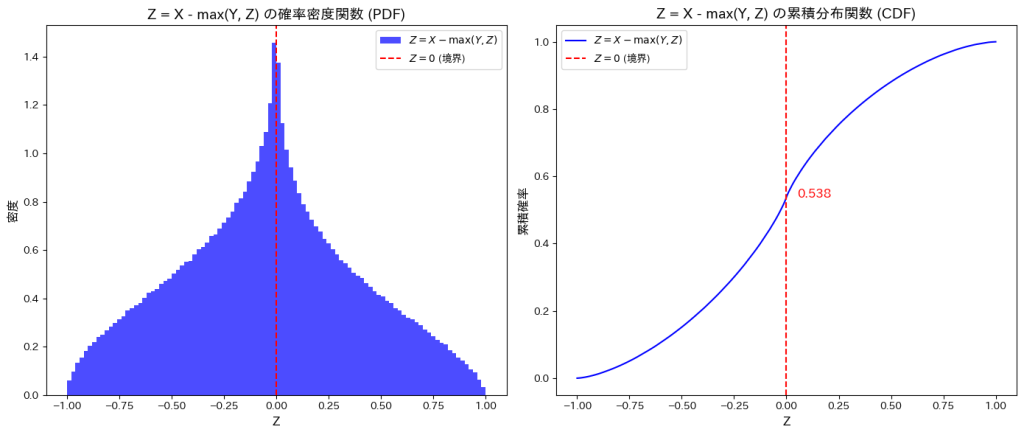
![]() はシミュレーションの結果、理論値と一致しました。
はシミュレーションの結果、理論値と一致しました。
2014 Q1(1)
一様分布の指数を取る二つの確率変数の大小が決まっている場合の確率を条件付確率の期待値を取ることで求めました。

コード
XとYの頻度分布を3Dプロットで可視化してみます。
# 2014 Q1(1) 2024.12.28
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# シミュレーションの設定
n_simulations = 10**5 # サンプルサイズ
# 一様分布からサンプリング
U = np.random.uniform(0, 1, n_simulations)
V = np.random.uniform(0, 1, n_simulations)
# X, Y の計算
X = U**2
Y = V**3
# 3Dプロット
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 2次元ヒストグラムを計算
hist, xedges, yedges = np.histogram2d(X, Y, bins=50, density=True)
# 座標軸を作成
xpos, ypos = np.meshgrid(xedges[:-1], yedges[:-1], indexing="ij")
xpos = xpos.ravel()
ypos = ypos.ravel()
zpos = np.zeros_like(xpos)
# 棒の高さ
dx = dy = 0.02
dz = hist.ravel()
# 色分け: X > Y (緑), X = Y (黄色), X < Y (青)
tolerance = 0.01 # 許容範囲を指定して X = Y の近似を表現
colors = np.where(
np.abs(xpos - ypos) < tolerance, 'yellow',
np.where(xpos > ypos, 'green', 'blue')
)
# 3Dバーを描画
ax.bar3d(xpos, ypos, zpos, dx, dy, dz, zsort='average', alpha=0.7, color=colors)
# ラベルとタイトル
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('頻度', labelpad=-10) # ラベルの位置を調整
#ax.set_title(r'$X > Y$ (緑), $X = Y$ (黄色), $X < Y$ (青)', fontsize=14)
#ax.set_title(r'$X$ と $Y$ の出現頻度', fontsize=14)
ax.set_title(r'$X$ と $Y$ の出現頻度(組)', fontsize=14)
# 凡例
legend_handles = [
plt.Line2D([0], [0], color='green', lw=4, label=r'$X > Y$ (緑)'),
plt.Line2D([0], [0], color='yellow', lw=4, label=r'$X = Y$ (黄色)'),
plt.Line2D([0], [0], color='blue', lw=4, label=r'$X < Y$ (青)')
]
ax.legend(handles=legend_handles, loc='upper left', bbox_to_anchor=(1.05, 1), fontsize=10)
# カメラビュー
ax.view_init(elev=30, azim=45)
plt.tight_layout()
plt.show()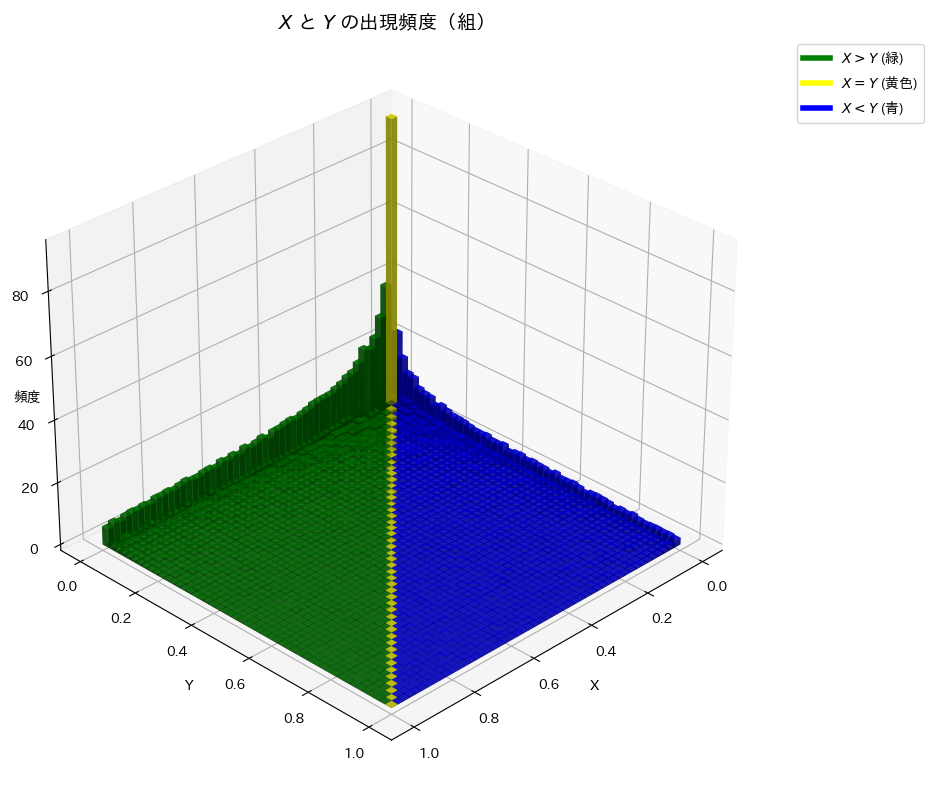
X>Yの領域は、X<Yの領域と比べて出現頻度が高いようです。
次に、XとYの大小関係を確認するために確率変数Z=X-Yを同に導入し、その確率密度と累積分布をシミュレーションにより求め、P(X>Y)を計算してみます。
# 2014 Q1(1) 2024.12.28
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
np.random.seed(42)
n_simulations = 10**6
# 一様分布からサンプリング
U = np.random.uniform(0, 1, n_simulations)
V = np.random.uniform(0, 1, n_simulations)
# X, Y の計算
X = U**2
Y = V**3
# Z = X - Y を計算
Z = X - Y
# Z の累積分布関数 (CDF) を計算
z_sorted = np.sort(Z)
cdf_Z = np.arange(1, len(z_sorted) + 1) / len(z_sorted)
# Z = 0 の累積確率を計算
cumulative_prob_at_zero = cdf_Z[np.searchsorted(z_sorted, 0)]
# 結果を出力
print(f"Z = 0 における累積確率: {cumulative_prob_at_zero:.3f}")
print(f"P(X > Y) = {1 - cumulative_prob_at_zero:.3f}")
# PDF および CDF のプロット (PDF にも Z = 0 の赤い線を追加)
plt.figure(figsize=(14, 6))
# PDF
plt.subplot(1, 2, 1)
plt.hist(Z, bins=100, density=True, alpha=0.7, label=r'$Z = X - Y$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)') # Z = 0 の赤い線を追加
plt.title('Z = X - Y の確率密度関数 (PDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()
# CDF
plt.subplot(1, 2, 2)
plt.plot(z_sorted, cdf_Z, label=r'$Z = X - Y$', color='blue')
plt.axvline(x=0, color='red', linestyle='--', label=r'$Z = 0$ (境界)') # Z = 0 の赤い線
plt.text(0.05, cumulative_prob_at_zero, f'{cumulative_prob_at_zero:.3f}', color='red', fontsize=12)
plt.title('Z = X - Y の累積分布関数 (CDF)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('累積確率', fontsize=12)
plt.legend()
plt.tight_layout()
plt.show()Z = 0 における累積確率: 0.399
P(X > Y) = 0.601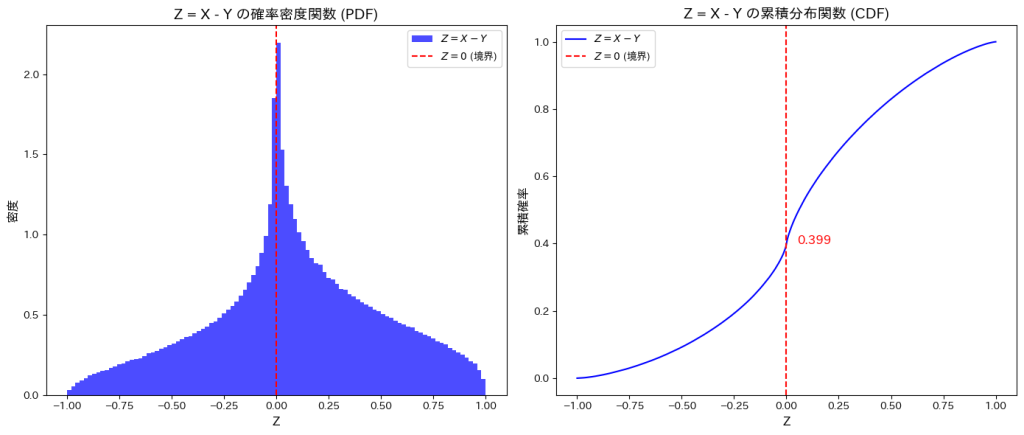
シミュレーションにより求めたP(X>Y)は、理論値と一致することが確認できました。
2015 Q4(2)
確率の分割表に対称性があるという仮説の下での期待度数の最尤推定を行いました。
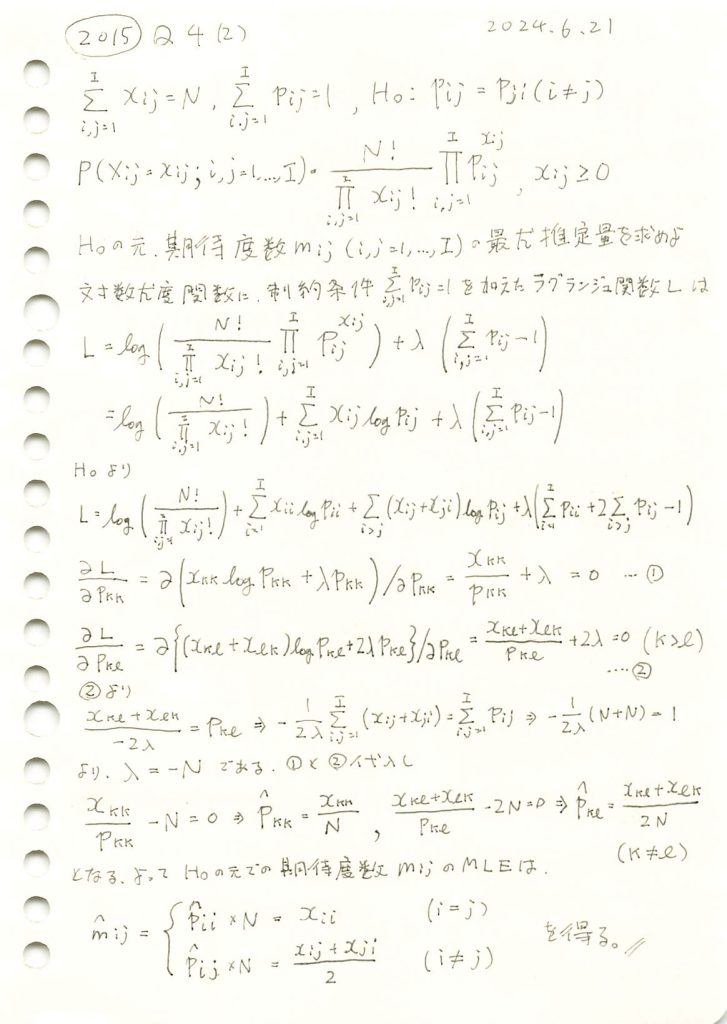
与えられた観測度数表から![]() に基づき期待度数を求めます。
に基づき期待度数を求めます。
# 2015 Q4(2) 2024.12.18
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 1. 観測度数表
observed_counts = np.array([[1520, 266, 124, 66],
[234, 1512, 432, 78],
[117, 362, 1772, 205],
[36, 82, 179, 492]])
# 2. 総サンプルサイズ N
N = observed_counts.sum()
# 3. 期待度数 m_ij の計算 (対称性の仮説)
m_ij = np.zeros_like(observed_counts, dtype=float)
I = observed_counts.shape[0]
for i in range(I):
for j in range(I):
if i == j: # 対角要素
m_ij[i, j] = observed_counts[i, j]
else: # 非対角要素
m_ij[i, j] = (observed_counts[i, j] + observed_counts[j, i]) / 2
# 4. 観測度数と期待度数をDataFrameにまとめる
row_labels = col_labels = ["Highest", "Second", "Third", "Lowest"]
df_observed = pd.DataFrame(observed_counts, index=row_labels, columns=col_labels)
df_expected = pd.DataFrame(np.round(m_ij, 2), index=row_labels, columns=col_labels)
# 5. 観測度数と期待度数のヒートマップを作成
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
# 観測度数のヒートマップ
sns.heatmap(df_observed, annot=True, fmt=".0f", cmap="Blues", ax=axes[0])
axes[0].set_title("観測度数表 $x_{ij}$")
# 期待度数のヒートマップ
sns.heatmap(df_expected, annot=True, fmt=".2f", cmap="Greens", ax=axes[1])
axes[1].set_title("期待度数表 $\hat{m}_{ij}$ (対称性の仮説)")
plt.tight_layout()
plt.show()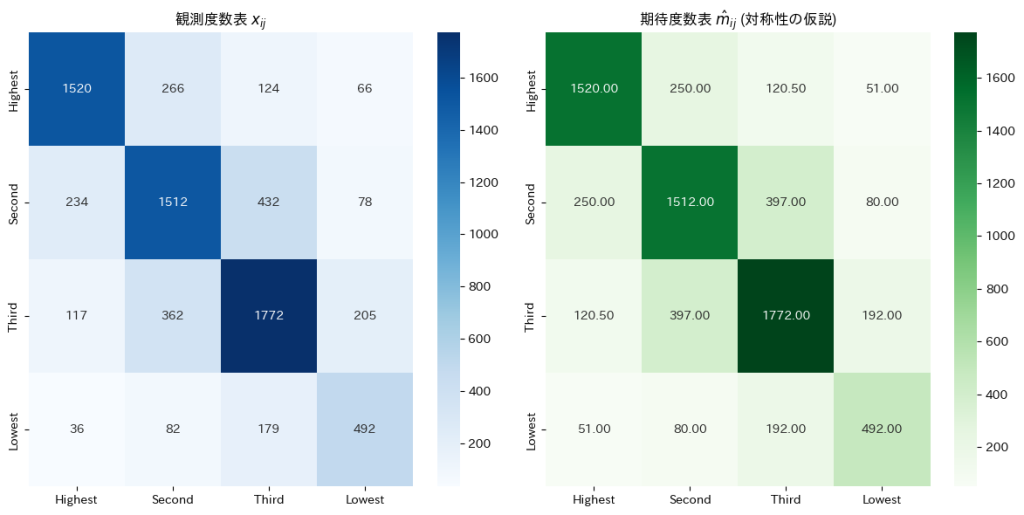
与えられた観測度数表から![]() に基づいて期待度数を求めると、非対角要素は対応する2つの観測度数の平均として表され、対角要素は観測度数そのものが期待度数となりました。
に基づいて期待度数を求めると、非対角要素は対応する2つの観測度数の平均として表され、対角要素は観測度数そのものが期待度数となりました。
2015 Q4(1)
観測度数と確率の分割表から、そうなり得る確率を求めました。

コード
与えられた観測度数表から仮にセル確率を計算し、その観測度数が多項分布に基づいて得られる確率を計算をします。
# 2015 Q4(1) 2024.12.17
import numpy as np
import pandas as pd
from scipy.stats import multinomial
# 観測度数表 (与えられたデータ)
observed_counts = np.array([[1520, 266, 124, 66],
[234, 1512, 432, 78],
[117, 362, 1772, 205],
[36, 82, 179, 492]])
# 総サンプルサイズ N の計算
N = observed_counts.sum()
# セル確率 pij の計算 (観測度数を総数で割る)
p_ij = observed_counts / N
# 観測度数とセル確率
row_labels = ["Highest", "Second", "Third", "Lowest"]
col_labels = ["Highest", "Second", "Third", "Lowest"]
# 観測度数
df_counts = pd.DataFrame(observed_counts, columns=col_labels, index=row_labels)
# セル確率
df_probs = pd.DataFrame(np.round(p_ij, 6), columns=col_labels, index=row_labels)
print("観測度数表 (x_ij):")
print(df_counts)
print("\nセル確率表 (p_ij):")
print(df_probs)
# 観測度数が得られる確率を計算
x_flat = observed_counts.flatten()
p_flat = p_ij.flatten()
# 多項分布の確率を計算
prob = multinomial.pmf(x_flat, n=N, p=p_flat)
print(f"\nこの観測度数表が得られる確率: {prob:.10e}")観測度数表 (x_ij):
Highest Second Third Lowest
Highest 1520 266 124 66
Second 234 1512 432 78
Third 117 362 1772 205
Lowest 36 82 179 492
セル確率表 (p_ij):
Highest Second Third Lowest
Highest 0.203290 0.035576 0.016584 0.008827
Second 0.031296 0.202220 0.057777 0.010432
Third 0.015648 0.048415 0.236993 0.027417
Lowest 0.004815 0.010967 0.023940 0.065802
この観測度数表が得られる確率: 7.0375704386e-24得られた確率はとても小さな数字になりました。これは、特定の具体的な度数の組み合わせが発生する確率であるため小さくなります。
2015 Q1(1)
任意の分布に従う確率変数の平均の二乗の期待値を求めました。
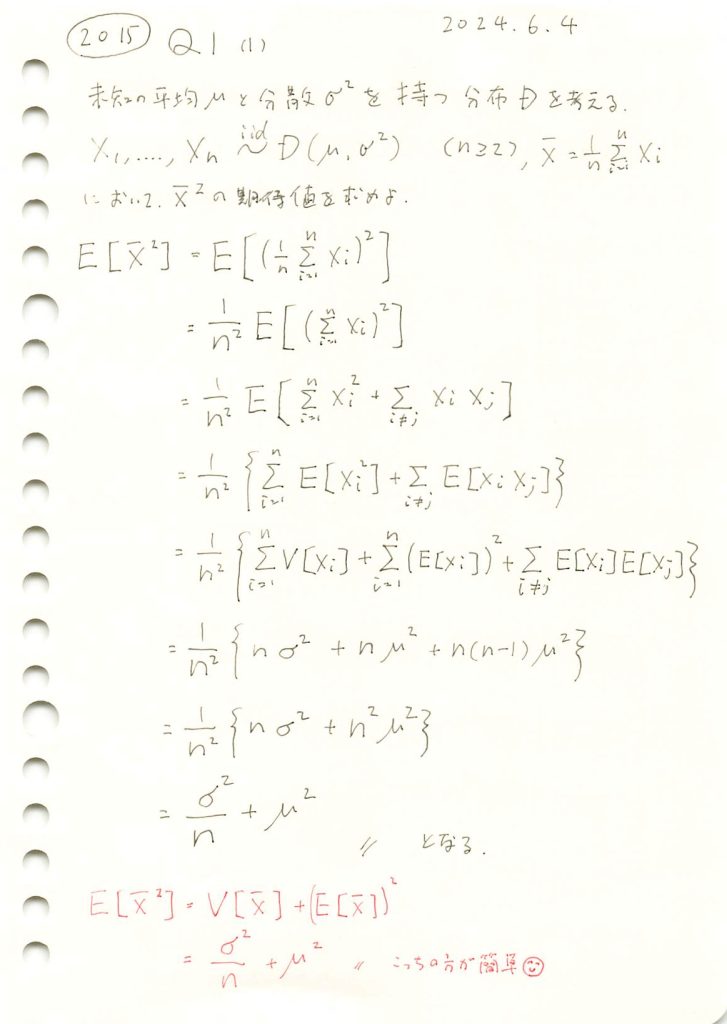
コード
![]() を確かめるためにシミュレーションを行います。nを変化させながら乱数を発生させ、計算した
を確かめるためにシミュレーションを行います。nを変化させながら乱数を発生させ、計算した![]() を理論値(非心カイ二乗分布)と比較し、プロットしてみます。
を理論値(非心カイ二乗分布)と比較し、プロットしてみます。
#2015 Q1(1) 2024.12.2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import ncx2
# パラメータ設定(nを複数用意)
n_values = [5, 10, 20, 50] # 標本サイズのリスト
mu = 4 # 母平均
sigma2 = 5 # 母分散
sigma = np.sqrt(sigma2) # 母標準偏差
num_simulations = 10000 # シミュレーション回数
# 暖色系カラーパレットの設定
colors = plt.cm.autumn(np.linspace(0, 1, len(n_values)))
# 描画の準備
plt.figure(figsize=(10, 8))
# 結果格納用
results = []
# nごとに分布をシミュレーションし、プロット
for i, n in enumerate(n_values):
# シミュレーションによる標本平均の二乗 (X̄^2) の生成
sample_means_squared = np.array([
np.mean(np.random.normal(mu, sigma, n))**2 for _ in range(num_simulations)
])
# シミュレーションによる期待値 E[X̄^2] の計算
simulated_mean = np.mean(sample_means_squared)
# 理論値の計算
theoretical_mean = sigma2 / n + mu**2
# 結果を記録
results.append((n, theoretical_mean, simulated_mean))
# ヒストグラムをプロット
plt.hist(
sample_means_squared, bins=30, density=True, alpha=0.5,
label=f"n={n}, 理論値: {theoretical_mean:.3f}, シミュレーション値: {simulated_mean:.3f}",
color=colors[i]
)
# 非心カイ二乗分布のPDFをプロット
x_values = np.linspace(0, np.max(sample_means_squared), 1000)
df = 1 # 自由度は標本平均の二乗の場合、1となる
nc = (n * mu**2) / sigma2 # 非心度 λ
theoretical_pdf = ncx2.pdf(x_values, df, nc, scale=sigma2 / n)
plt.plot(
x_values, theoretical_pdf, linewidth=2, label=f"n={n} の非心カイ二乗分布", color=colors[i]
)
# グラフ
plt.title("標本平均の二乗 ($\\overline{X}^2$) の分布と非心カイ二乗分布")
plt.xlabel("$\\overline{X}^2$")
plt.ylabel("密度")
plt.legend()
plt.grid()
plt.show()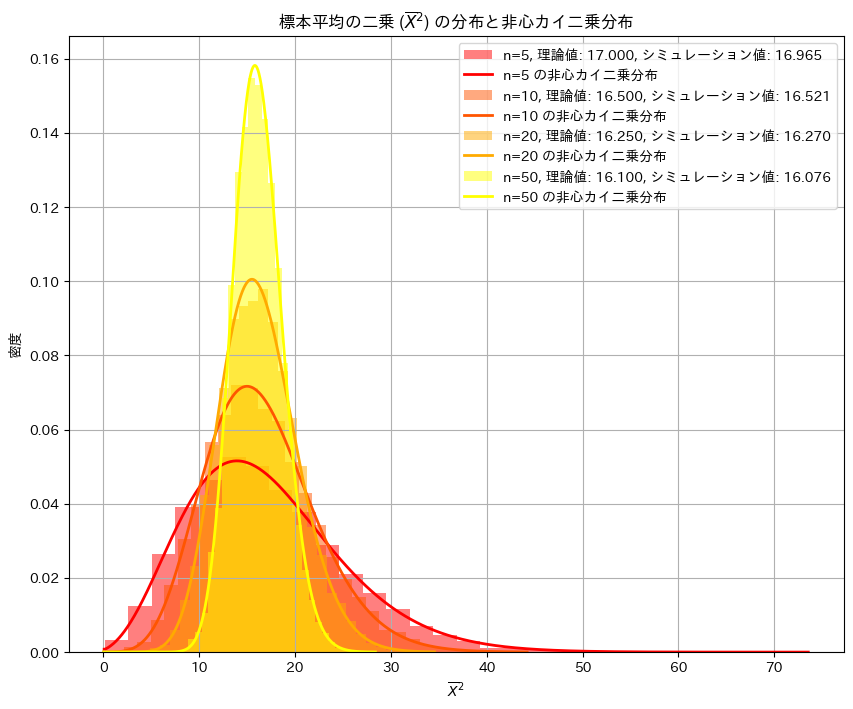
シミュレーションの結果、![]() と
と![]() は概ね一致しました。また
は概ね一致しました。また![]() の分布は理論値(非心カイ二乗分布)の形状とよく重なっていることが確認できました。
の分布は理論値(非心カイ二乗分布)の形状とよく重なっていることが確認できました。
2016 Q5(4)(5)
欠測のメカニズムがMCARであるか検定する手法の有効性について学びました。

コード
MCARと非MCARの場合の![]() の分布を、棄却域とともに描画をしてみます。
の分布を、棄却域とともに描画をしてみます。
# 2016 Q5(4) 2024.11.30
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import f
# シミュレーションパラメータ
n = 100 # 全サンプル数
m = 60 # 観測可能なデータ数
repeats = 1000 # シミュレーション回数
alpha = 0.05 # 有意水準
# F分布の上位5%点を計算
df1 = 1 # F分布の分子自由度
df2 = n - 2 # F分布の分母自由度
F_critical = f.ppf(1 - alpha, dfn=df1, dfd=df2)
# d^2 の上位5%点を計算
d2_critical = (n - 1) * F_critical / (n - 2 + F_critical)
# MCARデータの生成
def generate_mcar_data(n, m):
X = np.random.normal(0, 1, n)
Y = np.random.normal(0, 1, n)
observed_indices = np.random.choice(n, m, replace=False) # ランダムにm個観測
X_obs, Y_obs = X[observed_indices], Y[observed_indices]
X_miss = np.delete(X, observed_indices) # 欠測部分
return X_obs, X_miss
# MCARではないデータの生成 (欠測がXに依存)
def generate_non_mcar_data(n, m):
X = np.random.normal(0, 1, n)
Y = np.random.normal(0, 1, n)
# ロジスティック関数を使用して、全実数を0~1の確率に変換
prob = 1 / (1 + np.exp(-X)) # Xに依存した欠測確率
observed_indices = np.random.choice(n, m, replace=False, p=prob / prob.sum())
X_obs, Y_obs = X[observed_indices], Y[observed_indices]
X_miss = np.delete(X, observed_indices) # 欠測部分
return X_obs, X_miss
# d^2 の計算
def calculate_d2(X_obs, X_miss):
n = len(X_obs) + len(X_miss)
m = len(X_obs)
X_bar = np.mean(np.concatenate([X_obs, X_miss]))
X_obs_bar = np.mean(X_obs)
X_miss_bar = np.mean(X_miss)
S2 = np.var(np.concatenate([X_obs, X_miss]), ddof=1)
d2 = (1 / S2) * (m * (X_obs_bar - X_bar)**2 + (n - m) * (X_miss_bar - X_bar)**2)
return d2
# MCARデータと非MCARデータで帰無仮説を棄却した割合を計算
results_mcar = [calculate_d2(*generate_mcar_data(n, m)) > d2_critical for _ in range(repeats)]
results_non_mcar = [calculate_d2(*generate_non_mcar_data(n, m)) > d2_critical for _ in range(repeats)]
# 結果を出力
mcar_rejection_rate = np.mean(results_mcar) * 100 # 棄却率 (%)
non_mcar_rejection_rate = np.mean(results_non_mcar) * 100 # 棄却率 (%)
print(f"MCARデータで帰無仮説を棄却した割合: {mcar_rejection_rate:.2f}%")
print(f"非MCARデータで帰無仮説を棄却した割合: {non_mcar_rejection_rate:.2f}%")
# MCARデータと非MCARデータのd^2値を収集
d2_values_mcar = [calculate_d2(*generate_mcar_data(n, m)) for _ in range(repeats)]
d2_values_non_mcar = [calculate_d2(*generate_non_mcar_data(n, m)) for _ in range(repeats)]
# 理論的なd^2の曲線を計算するためのx軸範囲を設定
x_theoretical = np.linspace(0, max(max(d2_values_mcar), max(d2_values_non_mcar)), 500)
# d^2の理論的な確率密度関数を計算
d2_pdf_theoretical = f.pdf(x_theoretical * (n - 2) / (n - 1 - x_theoretical), dfn=df1, dfd=df2)
scaling_factor = (n - 2) / (n - 1)
d2_pdf_theoretical *= scaling_factor
# ヒストグラムの可視化
plt.figure(figsize=(12, 6))
# MCARデータのヒストグラム
plt.hist(d2_values_mcar, bins=30, alpha=0.7, label="MCARデータ", color="blue", density=True)
# 非MCARデータのヒストグラム
plt.hist(d2_values_non_mcar, bins=30, alpha=0.7, label="非MCARデータ", color="orange", density=True)
# 理論的な曲線をプロット
plt.plot(x_theoretical, d2_pdf_theoretical, label="理論的な $d^2$ 分布", color="green", linewidth=2)
# 臨界値をラインで表示
plt.axvline(d2_critical, color="red", linestyle="--", label=r"$d^2$ の臨界値", linewidth=2)
# グラフの装飾
plt.title(r"$d^2$ の分布と理論曲線: MCAR vs 非MCAR", fontsize=14)
plt.xlabel(r"$d^2$ の値", fontsize=12)
plt.ylabel("密度", fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# x軸の範囲を制限
plt.xlim(0, 20)
plt.tight_layout()
plt.show()MCARデータで帰無仮説を棄却した割合: 4.10%
非MCARデータで帰無仮説を棄却した割合: 91.70%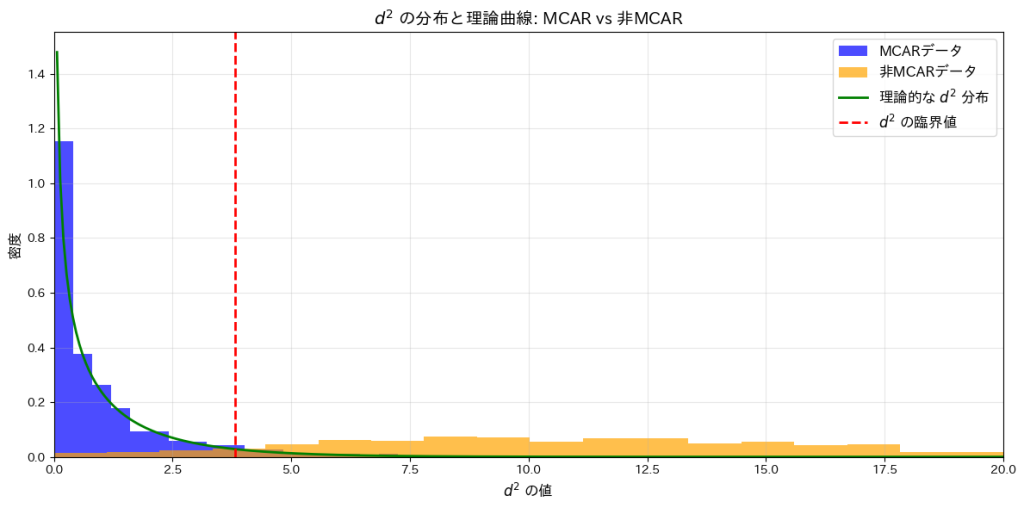
これらの結果から、有意水準を基準にした検定がMCARと非MCARの違いを正確に識別できることが確認されました。
次に、分散の違いを検出するため、非MCARの観測データと欠測データについてF検定を実施します。分布を可視化するとともに、F値とp値を計算して結果を確認します。
# 2016 Q5(5) 2024.12.1
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import f
# データ生成関数
def generate_non_mcar_data(n, m):
"""非MCARデータ生成: Xに依存して欠測"""
X = np.random.normal(0, 1, n) # 母集団は正規分布
Y = np.random.normal(0, 1, n) # ただし今回は使用しない
prob = 1 / (1 + np.exp(-5 * X)) # 欠測確率 (Xに依存)
observed_indices = np.random.choice(n, m, replace=False, p=prob / prob.sum())
X_obs = X[observed_indices]
X_miss = np.delete(X, observed_indices)
return X_obs, X_miss
# パラメータ設定
n = 100 # 全体のサンプル数
m = 60 # 観測されるサンプル数
# 非MCARデータ生成
X_obs, X_miss = generate_non_mcar_data(n, m)
# 平均と分散の計算
mean_obs = np.mean(X_obs)
var_obs = np.var(X_obs, ddof=1)
mean_miss = np.mean(X_miss)
var_miss = np.var(X_miss, ddof=1)
# F検定
F_statistic = var_obs / var_miss # F値
df1 = m - 1 # 観測データの自由度
df2 = n - m - 1 # 欠測データの自由度
p_value = 2 * min(f.cdf(F_statistic, df1, df2), 1 - f.cdf(F_statistic, df1, df2))
# 結果の表示
print(f"観測データの平均: {mean_obs:.5f}, 分散: {var_obs:.5f}")
print(f"欠測データの平均: {mean_miss:.5f}, 分散: {var_miss:.5f}")
print(f"F値: {F_statistic:.5f}")
print(f"p値: {p_value:.5f}")
# 可視化
plt.figure(figsize=(12, 6))
# ヒストグラムをプロット
plt.hist(X_obs, bins=15, alpha=0.7, label=f"観測データ (平均: {mean_obs:.2f}, 分散: {var_obs:.2f})", color="blue", density=True)
plt.hist(X_miss, bins=15, alpha=0.7, label=f"欠測データ (平均: {mean_miss:.2f}, 分散: {var_miss:.2f})", color="orange", density=True)
# グラフ設定
plt.title("非MCARの観測データと欠測データの分布", fontsize=14)
plt.xlabel("値", fontsize=12)
plt.ylabel("密度", fontsize=12)
plt.legend(fontsize=10)
plt.grid(alpha=0.3)
plt.show()観測データの平均: 0.67735, 分散: 0.55682
欠測データの平均: -0.88573, 分散: 0.46808
F値: 1.18958
p値: 0.57003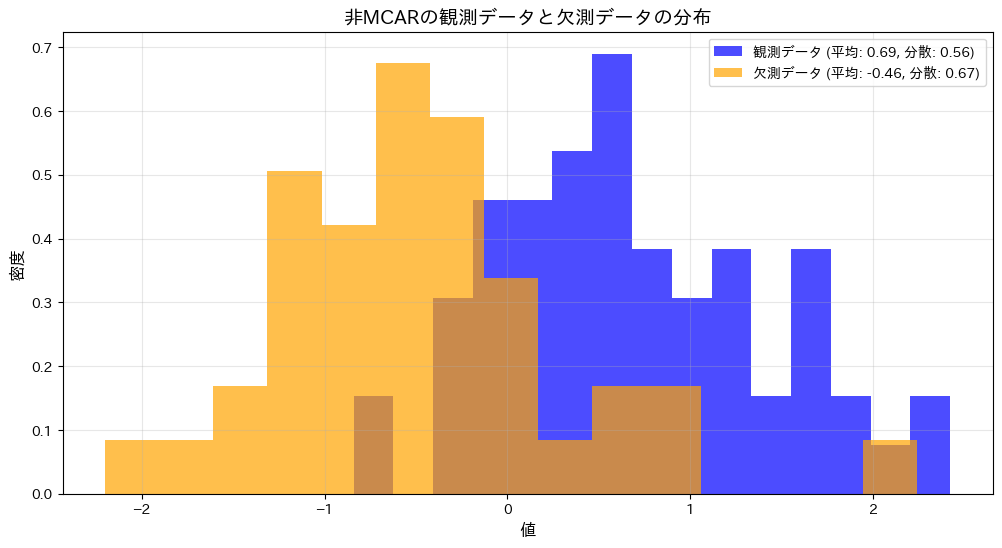
p値0.57003は有意水準を大きく上回り、非MCARの観測データと欠測データの分散に統計的な差があるとは言えません。また、グラフからも両者のばらつきに大きな違いがないことが視覚的に確認されました。
2016 Q5(3)
2群の一元配置分散分析のF検定が、2群の差の両側T検定と、本質的に同等であることを示しました。

コード
t検定(自由度n-2)と F 検定(自由度1,n-2)の p 値が等しいかシミュレーションによって検証してみます。
# 2016 Q5(3) 2024.11.29
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, f
# シミュレーションパラメータ
n = 100 # サンプルサイズ
repeats = 10000 # シミュレーションの繰り返し回数
alpha = 0.05 # 有意水準
# 自由度
df1 = 1 # F検定の分子自由度
df2 = n - 2 # F検定の分母自由度(t分布の自由度と一致)
# 検定結果の一致数を記録
agreement_count = 0
# p値を格納するリスト
p_values_t = []
p_values_f = []
# シミュレーションを実行
for _ in range(repeats):
# 2群のデータを生成
group1 = np.random.normal(loc=0, scale=1, size=n // 2)
group2 = np.random.normal(loc=0, scale=1, size=n // 2)
# 群間平均差の標準誤差
pooled_var = ((np.var(group1, ddof=1) + np.var(group2, ddof=1)) / 2)
se = np.sqrt(pooled_var * 2 / (n // 2))
# t統計量
t_stat = (np.mean(group1) - np.mean(group2)) / se
t_squared = t_stat**2
# F統計量
f_stat = t_squared # t^2 = F の関係を利用
# 両検定のp値を計算
p_value_t = 2 * (1 - t.cdf(np.abs(t_stat), df=df2)) # 両側検定
p_value_f = 1 - f.cdf(f_stat, dfn=df1, dfd=df2) # F検定の片側p値
# p値を保存
p_values_t.append(p_value_t)
p_values_f.append(p_value_f)
# 両検定が同じ結論を出したか確認
reject_t = p_value_t < alpha # t検定の結果
reject_f = p_value_f < alpha # F検定の結果
if reject_t == reject_f:
agreement_count += 1
# 一致率を計算
agreement_rate = agreement_count / repeats
# 結果を出力
print(f"t^2 検定と F 検定が一致した割合: {agreement_rate:.2%}")
# 散布図を作成
plt.figure(figsize=(8, 6))
plt.scatter(p_values_t, p_values_f, alpha=0.5, s=10, label="p値の散布図")
plt.plot([0, 1], [0, 1], 'r--', label="$y=x$") # y=xの基準線
plt.title(r"t検定(自由度 $n-2$)と F 検定(自由度 1, $n-2$)の p 値の比較", fontsize=14)
plt.xlabel("t検定のp値", fontsize=12)
plt.ylabel("F検定のp値", fontsize=12)
plt.legend(fontsize=12) # 凡例を追加
plt.grid(alpha=0.3) # グリッドを薄く表示
plt.show()t^2 検定と F 検定が一致した割合: 100.00%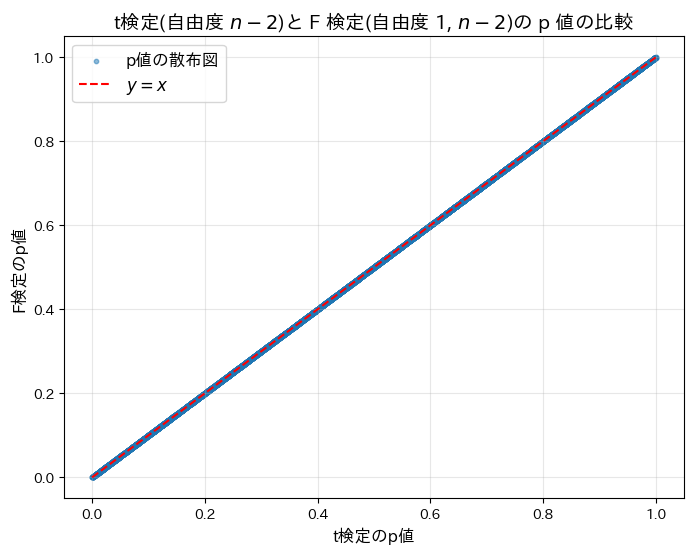
t検定(自由度n-2)と F 検定(自由度1,n-2)の p 値が等しいことがシミュレーションによって確認されました。両検定が同等であることが示されました。
次に、t分布(自由度n-2)と F分布(自由度1,n-2)を描画します。また、t分布の臨界点|t|=1,2と、対応するF分布の臨界点F=1,4(![]() に基づく)を示し、それらで区切られた領域の確率を計算し、それらを視覚的に確認してみます。
に基づく)を示し、それらで区切られた領域の確率を計算し、それらを視覚的に確認してみます。
# 2016 Q5(3) 2024.11.29
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, f
# パラメータ設定
n = 12 # サンプルサイズ(自由度は n-2)
df1 = 1 # F分布の分子自由度
df2 = n - 2 # t分布とF分布の分母自由度
x_t = np.linspace(-5, 5, 500) # t分布用のx軸範囲
x_f = np.linspace(0, 25, 500) # F分布用のx軸範囲
# t分布とF分布の確率密度関数を計算
t_pdf = t.pdf(x_t, df=df2) # t分布のPDF
f_pdf = f.pdf(x_f, dfn=df1, dfd=df2) # F分布のPDF
# t分布の新しい臨界点
critical_t_1 = 1 # ±1
critical_t_2 = 2 # ±2
# F分布の新しい臨界点
critical_f_1 = 1 # F=1
critical_f_2 = 4 # F=4
# P値の計算
# t分布のP値
p_t_between = 2 * (t.cdf(critical_t_2, df=df2) - t.cdf(critical_t_1, df=df2)) # 1 <= |t| <= 2
p_t_outside = 2 * (1 - t.cdf(critical_t_2, df=df2)) # |t| > 2
# F分布のP値
p_f_between = f.cdf(critical_f_2, dfn=df1, dfd=df2) - f.cdf(critical_f_1, dfn=df1, dfd=df2) # 1 <= F <= 4
p_f_outside = 1 - f.cdf(critical_f_2, dfn=df1, dfd=df2) # F > 4
# P値の結果を表示
print("t分布のP値:")
print(f" 1 <= |t| <= 2 の P値: {p_t_between:.5f}")
print(f" |t| > 2 の P値: {p_t_outside:.5f}")
print("\nF分布のP値:")
print(f" 1 <= F <= 4 の P値: {p_f_between:.5f}")
print(f" F > 4 の P値: {p_f_outside:.5f}")
# 可視化
plt.figure(figsize=(12, 6))
# t分布のプロット
plt.subplot(1, 2, 1)
plt.plot(x_t, t_pdf, label=r"$t$分布 (自由度 $n-2$)", color="blue")
plt.axvline(-critical_t_1, color="red", linestyle="--", label=r"臨界値 ($|t| = 1$)")
plt.axvline(critical_t_1, color="red", linestyle="--")
plt.axvline(-critical_t_2, color="orange", linestyle="--", label=r"臨界値 ($|t| = 2$)")
plt.axvline(critical_t_2, color="orange", linestyle="--")
plt.fill_between(x_t, t_pdf, where=(np.abs(x_t) <= critical_t_2) & (np.abs(x_t) >= critical_t_1), color="yellow", alpha=0.3, label=r"P値 ($1 \leq |t| \leq 2$)")
plt.fill_between(x_t, t_pdf, where=(np.abs(x_t) >= critical_t_2), color="orange", alpha=0.3, label=r"P値 ($|t| > 2$)")
plt.title("t分布と臨界値", fontsize=14)
plt.xlabel("t値", fontsize=12)
plt.ylabel("確率密度", fontsize=12)
plt.legend(fontsize=10)
plt.grid(alpha=0.3)
plt.xlim(-5, 5)
plt.ylim(0, 0.4)
# F分布のプロット
plt.subplot(1, 2, 2)
plt.plot(x_f, f_pdf, label=r"$F$分布 (自由度 $1, n-2$)", color="green")
plt.axvline(critical_f_1, color="red", linestyle="--", label=r"臨界値 ($F = 1$)")
plt.axvline(critical_f_2, color="orange", linestyle="--", label=r"臨界値 ($F = 4$)")
plt.fill_between(x_f, f_pdf, where=(x_f <= critical_f_2) & (x_f >= critical_f_1), color="yellow", alpha=0.3, label=r"P値 ($1 \leq F \leq 4$)")
plt.fill_between(x_f, f_pdf, where=(x_f >= critical_f_2), color="orange", alpha=0.3, label=r"P値 ($F > 4$)")
plt.title("F分布と臨界値", fontsize=14)
plt.xlabel("F値", fontsize=12)
plt.ylabel("確率密度", fontsize=12)
plt.legend(fontsize=10)
plt.grid(alpha=0.3)
plt.xlim(0, 10)
plt.ylim(0, 0.4)
plt.tight_layout()
plt.show()t分布のP値:
1 <= |t| <= 2 の P値: 0.26751
|t| > 2 の P値: 0.07339
F分布のP値:
1 <= F <= 4 の P値: 0.26751
F > 4 の P値: 0.07339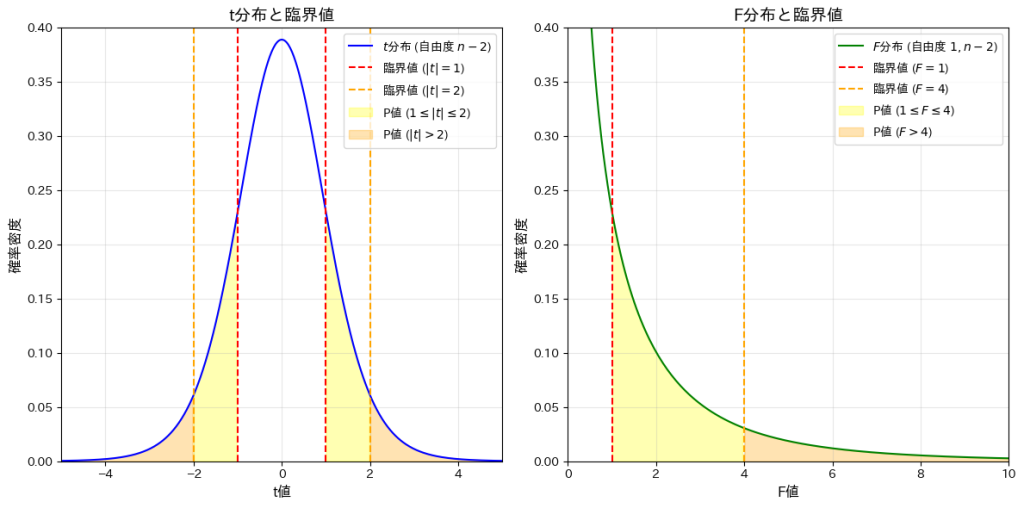
t分布の臨界で区切られた領域の確率と、それに対応するF分布の領域の確率が一致することを確認しました。
2016 Q4(2)
n個の標準正規分布に従う乱数が-1以上1以下となる個数が従う分布を求めました。また乱数が0以上1以下となる確率の推定値の分散を求めました。

コード
この実験では、標準正規分布N(0,1)と、n個の標準正規分布に従う乱数のうち-1以上1以下となる個数Yの分布、およびその確率を推定する量![]() の分布を確認します。
の分布を確認します。
# 2016 Q4(2) 2024.11.24
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, norm
# ---- グラフ 1: 標準正規分布 N(0,1) と範囲 (|Z| < 1) ----
# パラメータの設定
n_samples = 10000 # サンプル数
z_min, z_max = -1, 1 # 条件の範囲 (|Z| < 1)
# 標準正規分布 N(0,1) に従う乱数を生成します
samples = np.random.normal(0, 1, n_samples)
# 理論的な標準正規分布の確率密度関数を計算します
x1 = np.linspace(-4, 4, 500)
pdf_theoretical = norm.pdf(x1, loc=0, scale=1)
# ---- グラフ 2: Y の分布(二項分布) ----
# シミュレーションの設定
n_trials = 1000 # シミュレーションの試行回数
n = 50 # サンプルサイズ (1試行あたりの乱数生成数)
theta = 0.3413 # 真の成功確率 (0 < Z < 1)
# Y の分布を計算
Y_values = []
for _ in range(n_trials):
samples_trial = np.random.normal(0, 1, n)
Y = np.sum((samples_trial > z_min) & (samples_trial < z_max)) # 絶対値が1以下の個数
Y_values.append(Y)
# 理論的な二項分布
p_Y = 2 * theta # |Z| < 1 の確率
x2 = np.arange(0, n + 1)
binomial_pmf_Y = binom.pmf(x2, n, p_Y)
# ---- グラフ 3: θ̂2 の分布と理論分布 ----
# θ̂2 = Y / (2n) を計算
theta_hat_2_values = [Y / (2 * n) for Y in Y_values]
# 理論分布用のデータ
x3 = np.linspace(0, 1, 100)
binomial_pdf_theta_2 = norm.pdf(x3, loc=p_Y / 2, scale=np.sqrt(p_Y * (1 - p_Y) / (4 * n)))
# ---- 3つのグラフを描画 ----
plt.figure(figsize=(10, 12)) # グラフ全体のサイズを指定
# グラフ 1
plt.subplot(3, 1, 1)
plt.hist(samples, bins=50, density=True, alpha=0.5, label='全データ (N(0,1))', color='purple')
plt.axvspan(z_min, z_max, color='orange', alpha=0.3, label='|Z| < 1 の領域')
plt.plot(x1, pdf_theoretical, 'r-', label='理論分布 (N(0,1))', linewidth=2)
plt.title('N(0,1) に従う乱数のヒストグラムと領域', fontsize=14)
plt.xlabel('Z 値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフ 2
plt.subplot(3, 1, 2)
plt.hist(Y_values, bins=np.arange(0, n + 2) - 0.5, density=True, alpha=0.6, color='green', label='Y の分布 (シミュレーション)')
plt.plot(x2, binomial_pmf_Y, 'ro-', label='理論分布 (Binomial)', markersize=4)
plt.title('Y の分布と理論分布の比較', fontsize=14)
plt.xlabel('Y 値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフ 3
plt.subplot(3, 1, 3)
plt.hist(theta_hat_2_values, bins=10, density=True, alpha=0.6, color='blue', label='$\\hat{\\theta}_2$ の分布 (シミュレーション)')
plt.plot(x3, binomial_pdf_theta_2, 'r-', label='理論分布 $N(\\theta, V[\\hat{\\theta}_2])$', linewidth=2)
plt.title('$\\hat{\\theta}_2$ の分布と理論分布の比較', fontsize=14)
plt.xlabel('$\\hat{\\theta}_2$ 値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフを表示
plt.tight_layout() # 全体を整える
plt.show()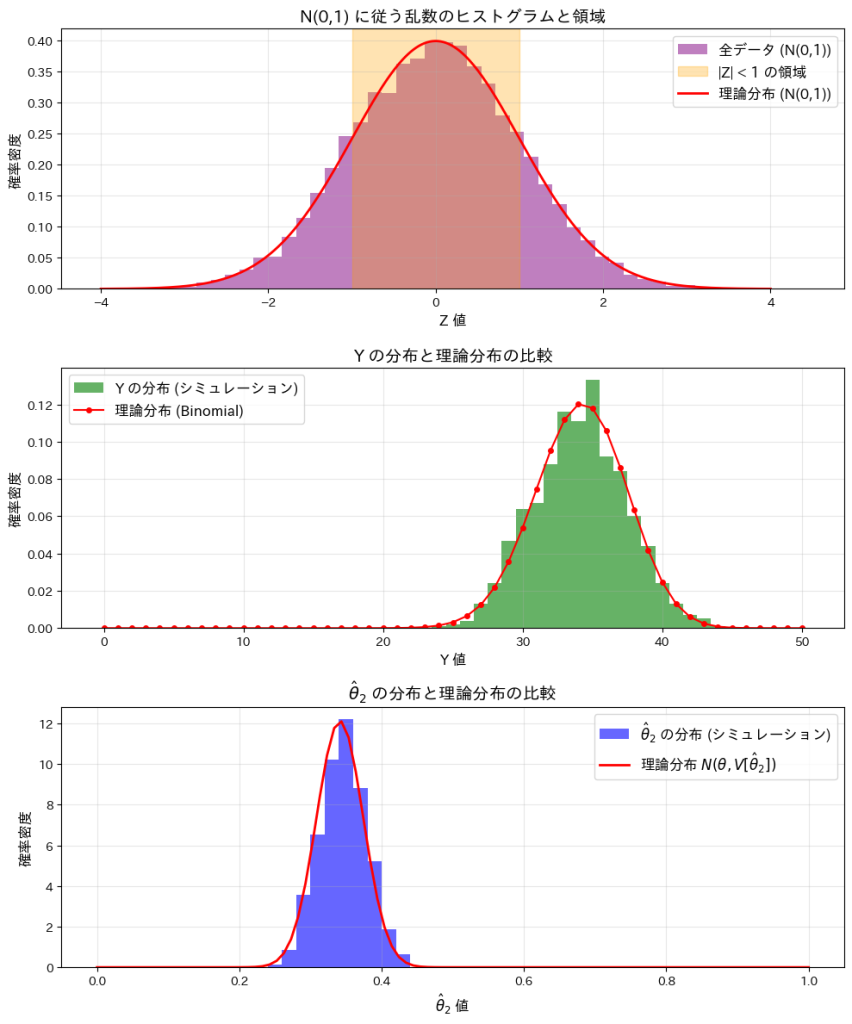
この実験によってYが二項分布B(n,2θ)に従うことと、![]() が正規分布
が正規分布![]() に従うことが確認できました。
に従うことが確認できました。