二項分布と超幾何分布
二項分布
- 抽出方法: 復元抽出
- 試行の独立性: 各試行は独立
- 確率: 各試行で成功確率は一定
超幾何分布
- 抽出方法: 非復元抽出
- 試行の独立性: 各試行は独立していない
- 確率: 各試行で成功確率が変化
グラフの比較
今回の実験では、二項分布と超幾何分布の違いを視覚的に比較します。二項分布は、復元抽出を行う場合に適用され、各試行が独立しており、成功確率が一定です。一方、超幾何分布は、非復元抽出を行う場合に適用され、試行ごとに成功確率が変化します。実験では、母集団のサイズ、成功対象の数、抽出回数を変え、それぞれのグラフを描画します。特に、サンプルサイズが大きい場合や母集団が小さい場合など、分布の形状に顕著な違いが現れる条件に注目して比較を行います。これにより、抽出方法による分布の違いを視覚的に確認し、二項分布と超幾何分布の特性を理解します。
復元抽出と非復元抽出の比較(広範囲のパラメータ設定)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, hypergeom
# グラフを描画する関数
def plot_comparison(M, N_A, n, ax):
# 非復元抽出(超幾何分布)
rv_hypergeom = hypergeom(M, N_A, n)
x_values = np.arange(0, n+1)
pmf_hypergeom = rv_hypergeom.pmf(x_values)
# 復元抽出(二項分布)
p = N_A / M # 豆Aを引く確率
rv_binom = binom(n, p)
pmf_binom = rv_binom.pmf(x_values)
# グラフ描画
ax.plot(x_values, pmf_hypergeom, 'bo-', label='非復元抽出 (超幾何分布)', markersize=5)
ax.plot(x_values, pmf_binom, 'ro-', label='復元抽出 (二項分布)', markersize=5)
condition_text = f'M = {M}, N_A = {N_A}, n = {n}'
ax.text(0.05, 0.95, condition_text, transform=ax.transAxes,
fontsize=12, verticalalignment='top')
ax.set_xlabel('豆Aの数')
ax.set_ylabel('確率')
ax.grid(True)
ax.legend()
# パラメータ比を一定に保ったグラフを作成
M_values = [50, 150, 250, 350, 450]
N_A_values = [15, 45, 75, 105, 135] # M の 30%
n_values = [7, 22, 37, 52, 67] # M の 15%
# サブプロットを作成(縦に並べる)
fig, axs = plt.subplots(5, 1, figsize=(10, 30))
# 異なるパラメータ設定でグラフを描画
for i in range(5):
plot_comparison(M=M_values[i], N_A=N_A_values[i], n=n_values[i], ax=axs[i])
# レイアウトの自動調整
plt.tight_layout()
# 余白の手動調整
plt.subplots_adjust(right=0.95)
plt.show()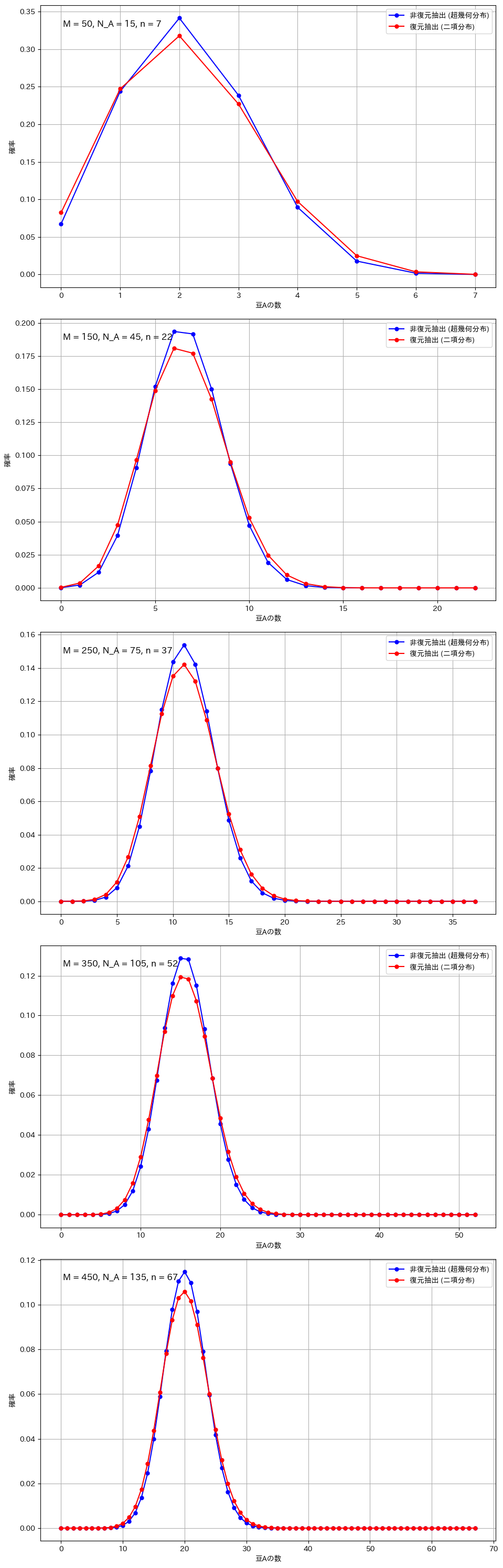
復元抽出と非復元抽出の比較(顕著な違いが現れる条件)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, hypergeom
# グラフを描画する関数
def plot_comparison(M, N_A, n, ax):
# 非復元抽出(超幾何分布)
rv_hypergeom = hypergeom(M, N_A, n)
x_values = np.arange(0, n+1)
pmf_hypergeom = rv_hypergeom.pmf(x_values)
# 復元抽出(二項分布)
p = N_A / M # 豆Aを引く確率
rv_binom = binom(n, p)
pmf_binom = rv_binom.pmf(x_values)
# グラフ描画
ax.plot(x_values, pmf_hypergeom, 'bo-', label='非復元抽出 (超幾何分布)', markersize=5)
ax.plot(x_values, pmf_binom, 'ro-', label='復元抽出 (二項分布)', markersize=5)
condition_text = f'M = {M}, N_A = {N_A}, n = {n}'
ax.text(0.05, 0.95, condition_text, transform=ax.transAxes,
fontsize=12, verticalalignment='top')
ax.set_xlabel('豆Aの数')
ax.set_ylabel('確率')
ax.grid(True)
ax.legend()
# サブプロットを作成(縦に並べる)
fig, axs = plt.subplots(3, 1, figsize=(10, 18)) # 高さを調整
# 条件1: サンプルサイズが大きい場合
plot_comparison(M=100, N_A=30, n=80, ax=axs[0])
# 条件2: 全体のサイズが小さい場合
plot_comparison(M=20, N_A=6, n=15, ax=axs[1])
# 条件3: 極端な割合の場合
plot_comparison(M=100, N_A=90, n=30, ax=axs[2])
# レイアウトの自動調整
plt.tight_layout()
# 余白の手動調整
plt.subplots_adjust(right=0.95)
plt.show()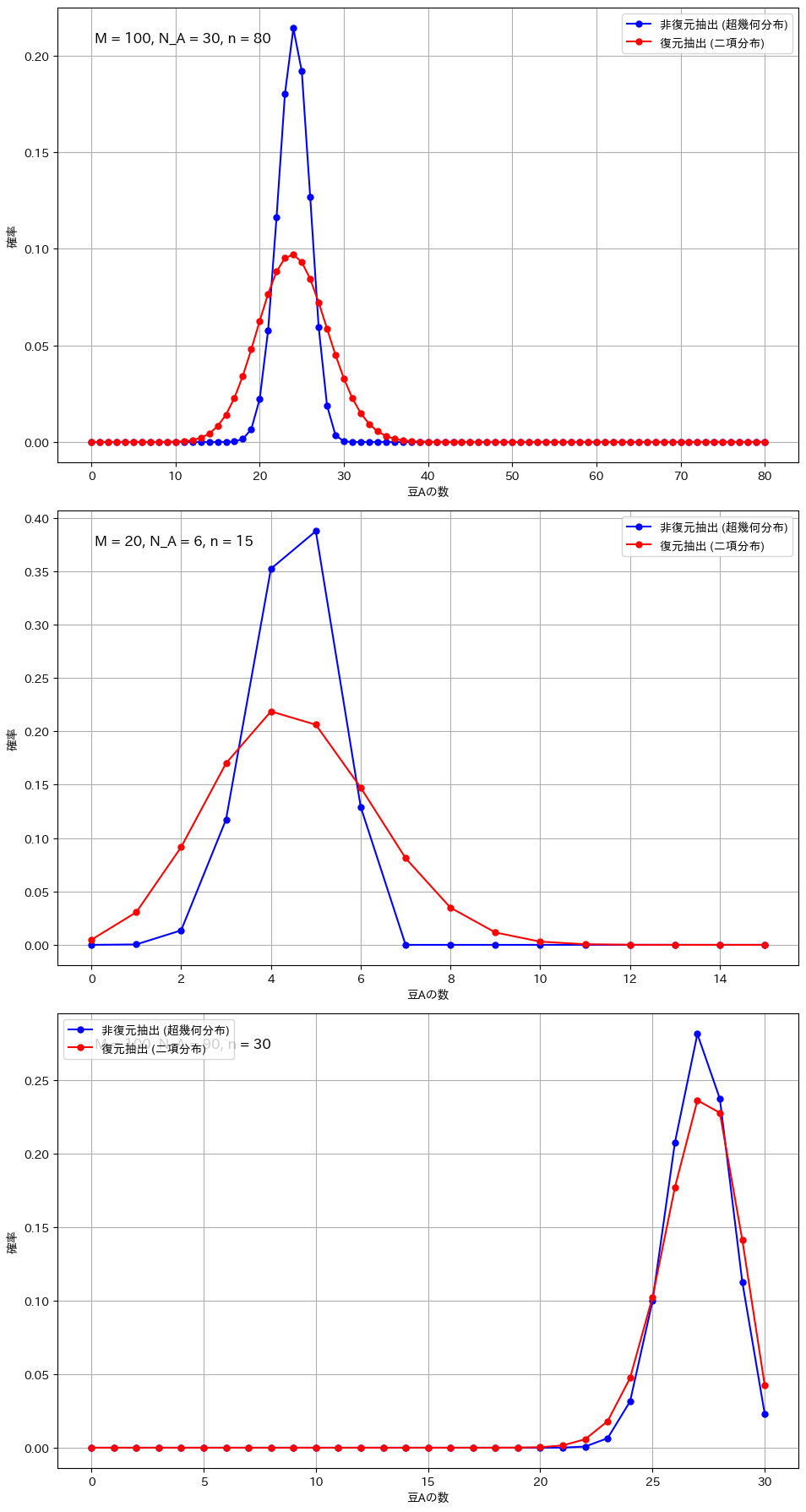
考察
二項分布と超幾何分布の違いが顕著になるのは、サンプルサイズが全体に対して大きい場合や、母集団が小さい場合です。例えば、全体の豆の数が100個で80個を抽出する場合や、母集団が20個でそのうち15個を抽出する場合、非復元抽出では次の試行に与える影響が大きくなり、復元抽出との差が明確に現れます。また、成功確率が極端に高いか低い場合も、非復元抽出の影響で分布が変わりやすくなります。一方、サンプルサイズが小さい場合や母集団が非常に大きい場合には、各抽出の影響が少なく、二項分布と超幾何分布の違いは目立たなくなります。
2018 Q2(5)-2
漸近分散の相対標準偏差を求める問題をやりました。

コード
NとMを変化させてシミュレーションし![]() の分布を描画しました。
の分布を描画しました。![]() を求め、理論値と一致するか確認してみます。
を求め、理論値と一致するか確認してみます。
# 2018 Q2(5)-2 2024.10.10
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_true = 1000 # 真の青球の数 N (これを推定する)
K_values = [100, 300, 500] # 赤球の数 K のバリエーション
n_values = [100, 200, 300] # 抽出する回数 n のバリエーション
n_trials = 10000 # シミュレーションの試行回数
# グラフレイアウト設定
fig, axes = plt.subplots(len(K_values), len(n_values), figsize=(15, 12))
axes = axes.flatten()
plot_idx = 0
# 各 K, n の組み合わせに対してシミュレーションを実行
for K in K_values:
for n in n_values:
N_hat_values = []
for _ in range(n_trials):
# 青球 N 個 + 赤球 K 個のボールを作成
balls = [0] * N_true + [1] * K # 0が青球、1が赤球
drawn_balls = np.random.choice(balls, size=n, replace=False) # 非復元抽出
X = np.sum(drawn_balls) # 抽出された赤球の個数
# X を使って N の推定量 N_hat を計算
if X > 0: # Xが0でない場合
N_hat = K * (n - X) / X
N_hat_values.append(N_hat)
# シミュレーション結果から N_hat の分散を計算
N_hat_var = np.var(N_hat_values)
# 理論値 ε の計算
epsilon_theory = np.sqrt((N_true + K) * (N_true + K - n) / (n * N_true * K))
# シミュレーションから求めた ε の計算
epsilon_simulation = np.sqrt(N_hat_var) / N_true
# 推定量 N_hat の分布をヒストグラムで表示
ax = axes[plot_idx]
ax.hist(N_hat_values, bins=100, density=True, alpha=0.7, color='b', edgecolor='black')
ax.axvline(x=N_true, color='r', linestyle='--') # 真の N を破線で表示
ax.set_title(f'K={K}, n={n}')
ax.set_xlabel('推定量 N_hat')
ax.set_ylabel('確率密度')
# εの値と真のNをまとめて表示
ax.text(0.95, 0.95, f'真の N = {N_true}\nε (理論) = {epsilon_theory:.4f}\nε (シミュ) = {epsilon_simulation:.4f}',
transform=ax.transAxes, verticalalignment='top', horizontalalignment='right',
bbox=dict(facecolor='white', alpha=0.7), fontsize=10)
ax.grid(True)
plot_idx += 1
# グラフ全体の調整
plt.tight_layout()
plt.show()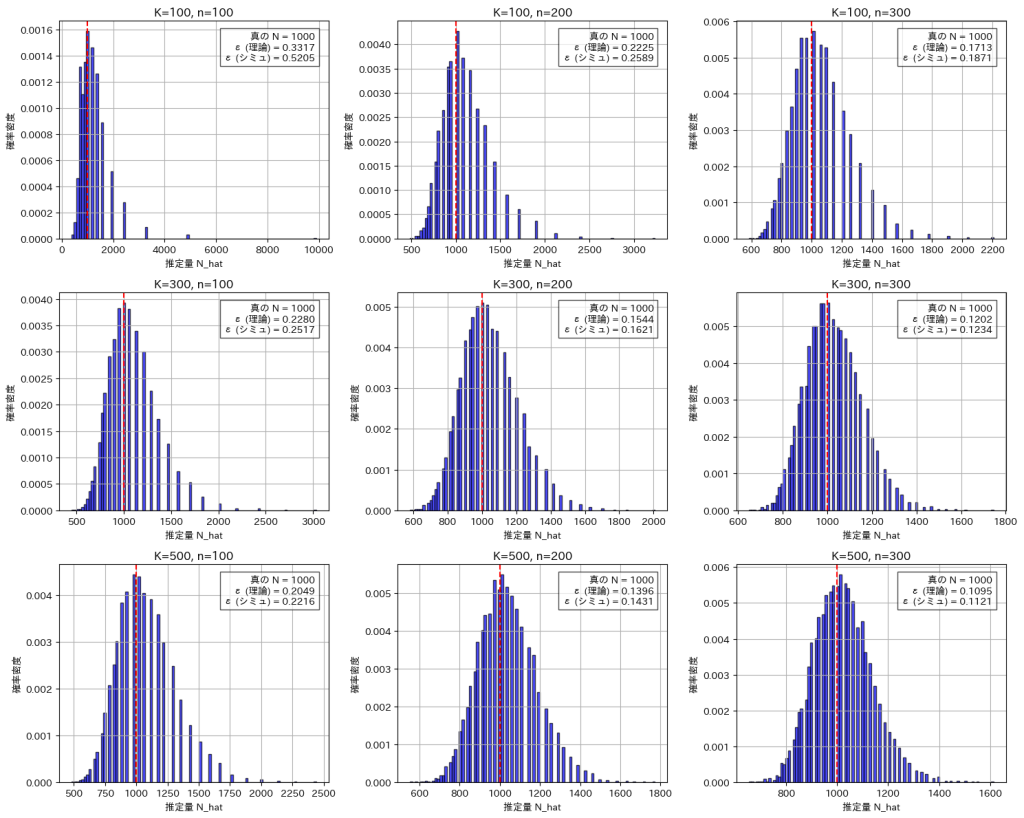
シミュレーションによる結果は理論値と概ね一致しました。
2018 Q2(5)-1
非復元無作為抽出による未知の母数N個の推定を行いました。

コード
複数回シミュレーションし![]() のヒストグラムを描画します。
のヒストグラムを描画します。
# 2018 Q2(5)-1 2024.10.9
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_true = 100 # 真の青球の数 N (これを推定する)
K = 30 # 赤球の数 K (既知)
n = 20 # 抽出する回数
n_trials = 10000 # シミュレーションの試行回数
# 推定量 Nハットのシミュレーション
N_hat_values = []
for _ in range(n_trials):
# 青球 N 個 + 赤球 K 個のボールを作成
balls = [0] * N_true + [1] * K # 0が青球、1が赤球
drawn_balls = np.random.choice(balls, size=n, replace=False) # 非復元抽出
X = np.sum(drawn_balls) # 抽出された赤球の個数
# X を使って N の推定量 N_hat を計算
if X > 0: # Xが0でない場合
N_hat = K * (n - X) / X
N_hat_values.append(N_hat)
# シミュレーション結果の分析
N_hat_mean = np.mean(N_hat_values)
N_hat_var = np.var(N_hat_values)
# 結果表示
print(f"推定量 N_hat の平均: {N_hat_mean}")
print(f"推定量 N_hat の分散: {N_hat_var}")
# ヒストグラム表示
plt.figure(figsize=(10, 6))
plt.hist(N_hat_values, bins=50, density=True, alpha=0.7, color='b', edgecolor='black')
plt.axvline(x=N_true, color='r', linestyle='--', label=f'真の N = {N_true}')
plt.title(f'推定量 N_hat の分布 (N={N_true}, K={K}, n={n})')
plt.xlabel('推定量 N_hat')
plt.ylabel('確率密度')
plt.legend()
plt.grid(True)
plt.show()推定量 N_hat の平均: 126.09541441704363
推定量 N_hat の分散: 8070.195087794488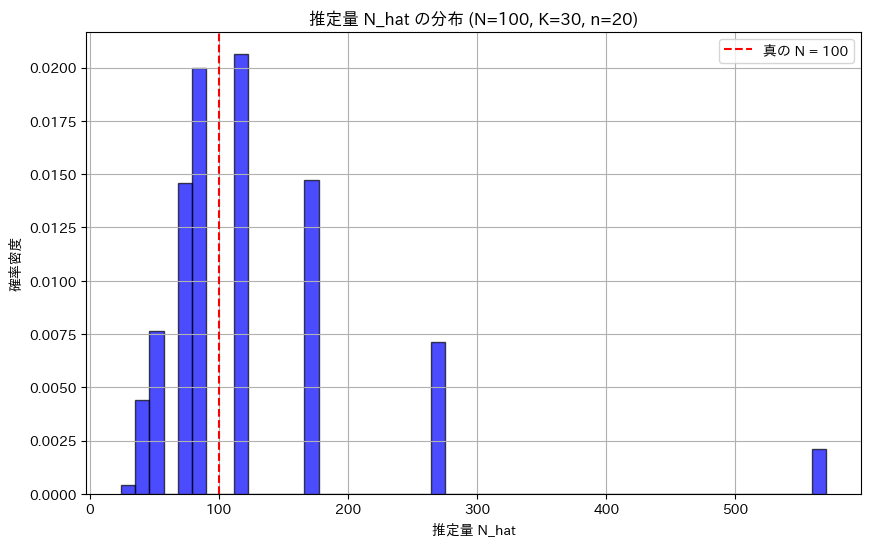
![]() は、真のNから離れた値も取ることがあり、特に飛び飛びの値を取りやすく、右側に裾が長い形をしていることが分かりました。
は、真のNから離れた値も取ることがあり、特に飛び飛びの値を取りやすく、右側に裾が長い形をしていることが分かりました。
2018 Q2(4)
超幾何分布の期待値と分散を求めました。

コード
NとMを変化させて期待値E[X]と分散V[X]についてシミュレーションを行い理論値と一致するか確認します。
# 2018 Q2(4) 2024.10.8
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数
n = 10 # 抽出回数
n_trials = 10000 # シミュレーションの試行回数
# グラフ描画の準備
plt.figure(figsize=(12, 8))
for N in N_values:
M_values = np.arange(M_steps, N + 1, M_steps) # 赤球数をステップで変化
# 理論値の計算
E_X_theory = n * M_values / N
V_X_theory = n * M_values / N * (N - M_values) / N * (N - n) / (N - 1)
# シミュレーションによる期待値と分散の計算
E_X_simulation = []
V_X_simulation = []
for M in M_values:
X_values = []
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M)
drawn_balls = np.random.choice(balls, size=n, replace=False)
X_values.append(np.sum(drawn_balls)) # 赤球の数
E_X_simulation.append(np.mean(X_values))
V_X_simulation.append(np.var(X_values))
# 期待値のグラフに追加描画
plt.subplot(2, 1, 1) # 期待値のグラフ (上側)
plt.plot(M_values, E_X_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, E_X_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
# 分散のグラフに追加描画
plt.subplot(2, 1, 2) # 分散のグラフ (下側)
plt.plot(M_values, V_X_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, V_X_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
# グラフの設定
plt.subplot(2, 1, 1)
plt.xlabel('赤球の数 (M)')
plt.ylabel('期待値 E[X]')
plt.title('異なる N における期待値 E[X] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.subplot(2, 1, 2)
plt.xlabel('赤球の数 (M)')
plt.ylabel('分散 V[X]')
plt.title('異なる N における分散 V[X] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()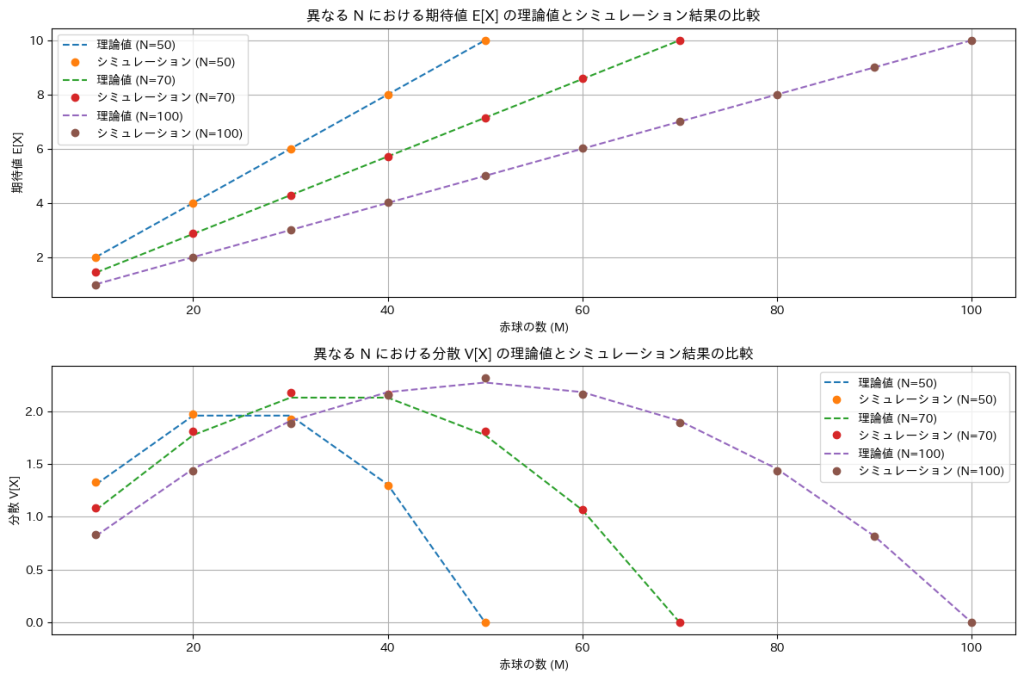
ミュレーションによる結果は理論値と一致しました。
2018 Q2(3)
非復元無作為抽出の当たり数を確率変数とする確率質量関数を求めました。

コード
超幾何分布HG(N,M,n)に従う確率変数XのシミュレーションをNとMを変化させて実行し理論値と一致するか確認してみます。
# 2018 Q2(3) 2024.10.7
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import hypergeom
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション (列ごとに固定)
M_values = [10, 20, 30, 40, 50] # 赤球の数 M のバリエーション (行ごとに変化)
n = 10 # 抽出する回数
n_trials = 10000 # シミュレーションの試行回数
# グラフのレイアウト設定 (5行x3列)
fig, axes = plt.subplots(5, 3, figsize=(15, 20)) # 5行3列のサブプロット
# 各 M に対してシミュレーションと理論値を計算
for row, M in enumerate(M_values): # 行が M を表す
for col, N in enumerate(N_values): # 列が N を表す
# 理論値の計算
x_values = np.arange(0, n + 1) # 可能な赤球の数 x の範囲
rv = hypergeom(N, M, n) # 超幾何分布のインスタンス
P_X_theory = rv.pmf(x_values) # 理論値(超幾何分布)
# シミュレーションによる確率計算
drawn_red_balls = []
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M) # 赤球 M 個、青球 N-M 個のリスト
drawn_balls = np.random.choice(balls, size=n, replace=False) # n 回非復元抽出
x = np.sum(drawn_balls) # 赤球の個数を数える
drawn_red_balls.append(x)
# 各サブプロットにグラフを描画
ax = axes[row, col]
ax.plot(x_values, P_X_theory, 'bo-', label=f'理論値 (N={N}, M={M})')
ax.hist(drawn_red_balls, bins=np.arange(-0.5, n + 1.5, 1), density=True, alpha=0.6, color='r', label='シミュレーション結果')
ax.set_xlabel('赤球の個数 (x)')
ax.set_ylabel('確率 P(X = x)')
ax.set_title(f'N={N}, M={M}, n={n}')
ax.grid(True)
# 全体のレイアウト調整
plt.tight_layout()
plt.show()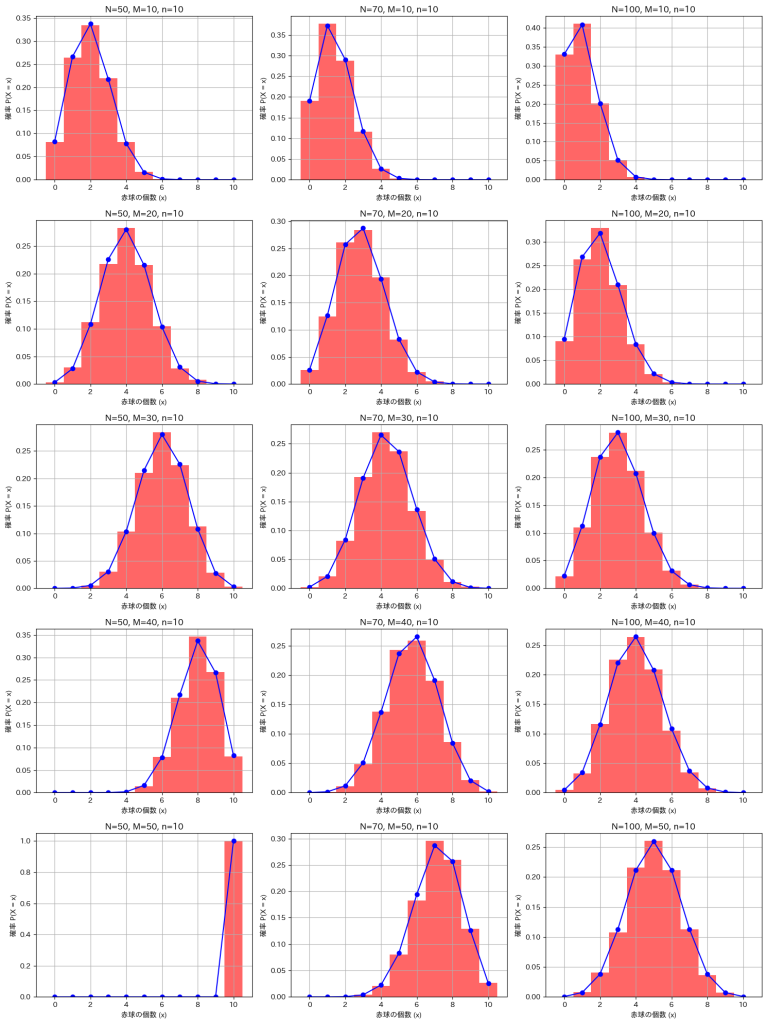
シミュレーションによる結果は理論値と一致しました。
2018 Q2(2)
非復元無作為抽出の期待値と分散と共分散を求めました。
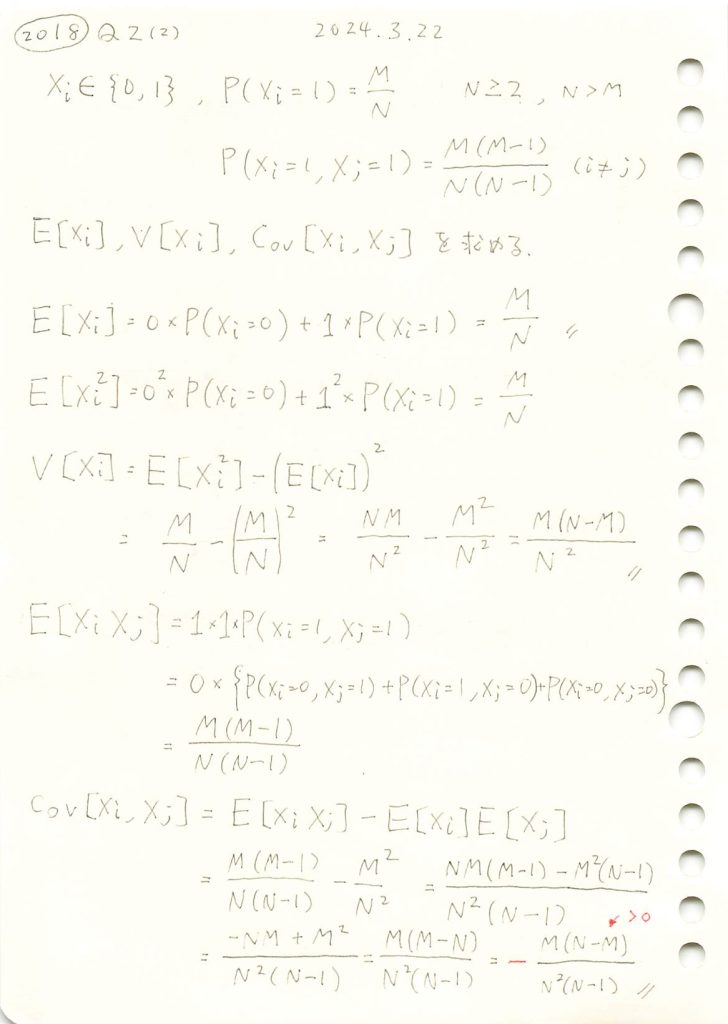
コード
NとMを変化させて期待値E[Xi]についてシミュレーションを行い理論値と一致するか確認します。
# 2018 Q2(2) 2024.10.6
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数
n_trials = 10000 # シミュレーションの試行回数
# 期待値 E[X_i] のグラフ描画
plt.figure(figsize=(10, 6))
for N in N_values:
M_values = np.arange(2, N + 1, M_steps) # 赤球数をステップで変化
# 理論値の計算
E_Xi_theory = M_values / N
# シミュレーションによる期待値の計算
E_Xi_simulation = []
for M in M_values:
count_Xi_1 = 0
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M)
drawn_ball = np.random.choice(balls, size=1, replace=False)
count_Xi_1 += drawn_ball[0]
E_Xi_simulation.append(count_Xi_1 / n_trials)
# グラフに追加描画
plt.plot(M_values, E_Xi_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, E_Xi_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
plt.xlabel('赤球の数 (M)')
plt.ylabel('期待値 E[X_i]')
plt.title('異なる N における 期待値 E[X_i] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()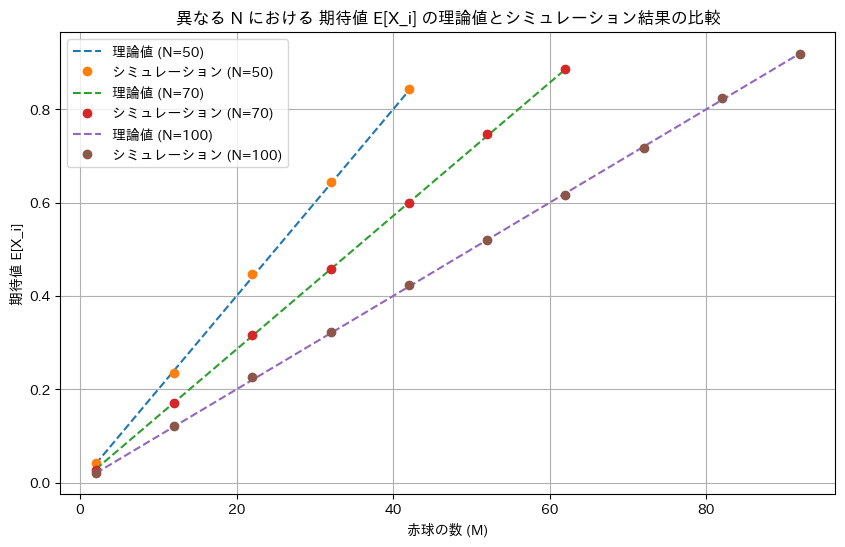
ミュレーションによる結果は理論値と一致しました。
次に、分散V[Xi]についてシミュレーションを行い理論値と一致するか確認します。
# 2018 Q2(2) 2024.10.6
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数
n_trials = 10000 # シミュレーションの試行回数
# 分散 V[X_i] のグラフ描画
plt.figure(figsize=(10, 6))
for N in N_values:
M_values = np.arange(2, N + 1, M_steps)
# 理論値の計算
V_Xi_theory = M_values * (N - M_values) / N**2
# シミュレーションによる分散の計算
V_Xi_simulation = []
for M in M_values:
Xi_values = []
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M)
drawn_ball = np.random.choice(balls, size=1, replace=False)
Xi_values.append(drawn_ball[0])
V_Xi_simulation.append(np.var(Xi_values))
# グラフに追加描画
plt.plot(M_values, V_Xi_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, V_Xi_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
plt.xlabel('赤球の数 (M)')
plt.ylabel('分散 V[X_i]')
plt.title('異なる N における 分散 V[X_i] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()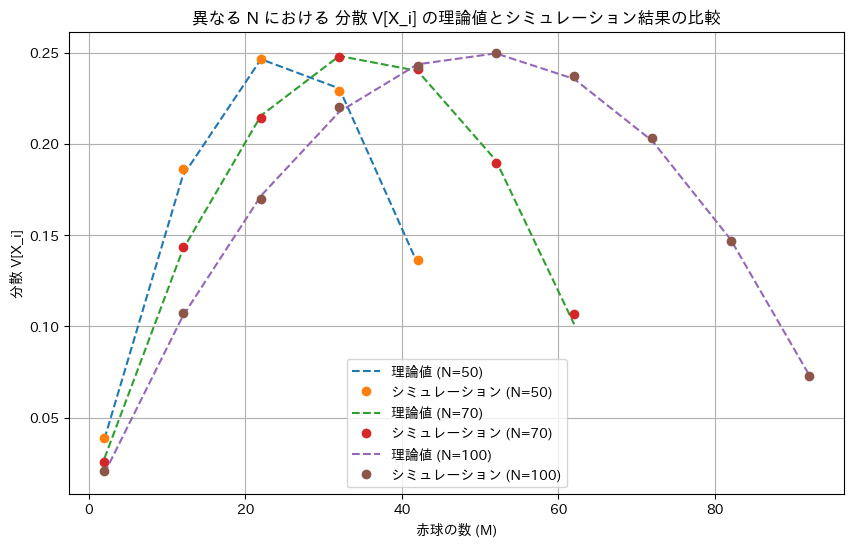
ミュレーションによる結果は理論値と一致しました。
次に、共分散Cov[Xi,Xj]についてシミュレーションを行い理論値と一致するか確認します。ただし、共分散は二変数を扱うため誤差が大きくなりやすいので、シミュレーションの試行回数を多め(1,000,000回)でやってみます。実行は環境により数十分かかることもあります。
# 2018 Q2(2) 2024.10.6
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数
n_trials = 1000000 # シミュレーションの試行回数
# 共分散 Cov[X_i, X_j] のグラフ描画
plt.figure(figsize=(10, 6))
for N in N_values:
M_values = np.arange(2, N + 1, M_steps)
# 理論値の計算
Cov_Xi_Xj_theory = -(M_values * (N - M_values)) / (N**2 * (N - 1))
# シミュレーションによる共分散の計算
Cov_Xi_Xj_simulation = []
for M in M_values:
Xi_values = []
Xj_values = []
for _ in range(n_trials):
balls = [1] * M + [0] * (N - M)
drawn_balls = np.random.choice(balls, size=2, replace=False)
Xi_values.append(drawn_balls[0])
Xj_values.append(drawn_balls[1])
Cov_Xi_Xj_simulation.append(np.cov(Xi_values, Xj_values)[0, 1])
# グラフに追加描画
plt.plot(M_values, Cov_Xi_Xj_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, Cov_Xi_Xj_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
plt.xlabel('赤球の数 (M)')
plt.ylabel('共分散 Cov[X_i, X_j]')
plt.title('異なる N における 共分散 Cov[X_i, X_j] の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()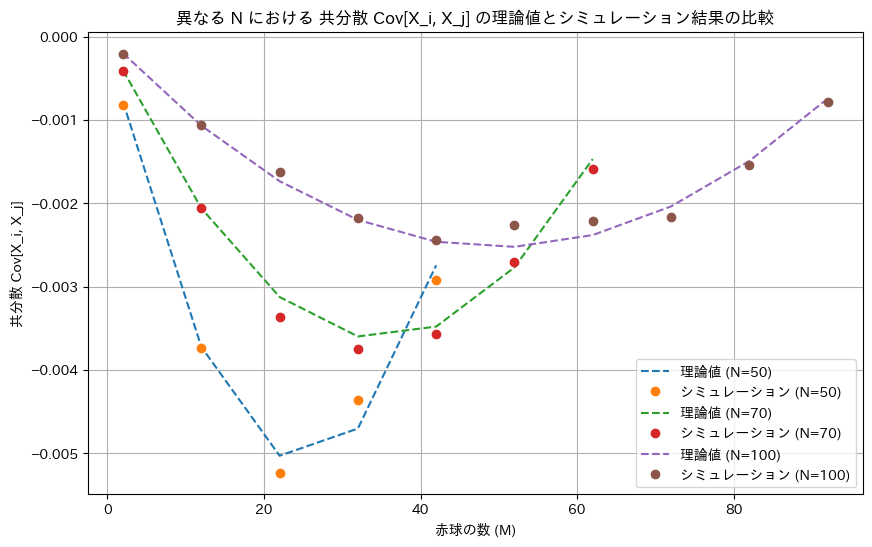
シミュレーションによる結果は概ね一致しました。
2018 Q2(1)-2
非復元無作為抽出でi番目とj番目が当たりになる確率を求めました。

コード
NとMを変化させてシミュレーションを行い理論値と一致するか確認します。
# 2018 Q2(1)-2 2024.10.5
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数を指定
n_trials = 10000 # シミュレーションの試行回数
# グラフ描画の準備
plt.figure(figsize=(10, 6))
# 各 N に対してシミュレーションと理論値を計算
for N in N_values:
M_values = np.arange(2, N + 1, M_steps) # 赤球数をステップで変化 (M >= 2 に設定)
# 理論値の計算
P_Xi_Xj_theory = (M_values / N) * ((M_values - 1) / (N - 1))
# シミュレーションによる確率計算
P_Xi_Xj_simulation = []
for M in M_values:
count_Xi_Xj_1 = 0
for _ in range(n_trials):
# 箱の中の球を準備(赤球 M 個、青球 N-M 個)
balls = [1] * M + [0] * (N - M)
# 非復元抽出で2つの球を無作為に抽出
drawn_balls = np.random.choice(balls, size=2, replace=False)
# 2回連続で赤球が引かれたか確認
if drawn_balls[0] == 1 and drawn_balls[1] == 1:
count_Xi_Xj_1 += 1
# シミュレーション結果の確率
P_Xi_Xj_simulation.append(count_Xi_Xj_1 / n_trials)
# グラフに追加描画
plt.plot(M_values, P_Xi_Xj_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, P_Xi_Xj_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
# グラフのラベルとタイトル設定
plt.xlabel('赤球の数 (M)')
plt.ylabel('P(X_i = 1, X_j = 1) の確率')
plt.title('異なる N における P(X_i = 1, X_j = 1) の理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()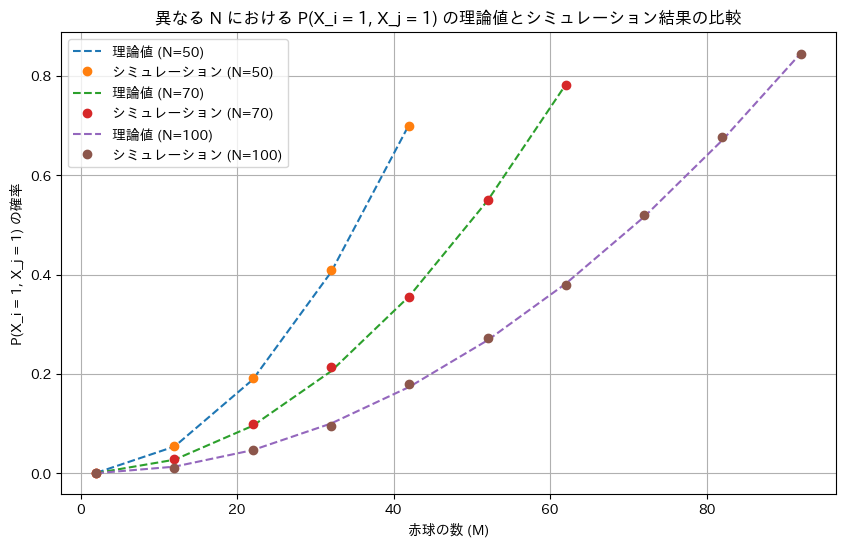
シミュレーションによる結果は理論値と一致しました。
2018 Q2(1)-1
非復元無作為抽出で当たりの出る確率を求めました。

コード
NとMを変化させてシミュレーションを行い理論値と一致するか確認します。
# 2018 Q2(1)-1 2024.10.5
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_values = [50, 70, 100] # 総球数 N のバリエーション
M_steps = 10 # 赤球のステップ数を指定
n_trials = 10000 # シミュレーションの試行回数
# グラフ描画の準備
plt.figure(figsize=(10, 6))
# 各 N に対してシミュレーションと理論値を計算
for N in N_values:
M_values = np.arange(1, N + 1, M_steps) # 赤球数をステップで変化
P_Xi_1_theory = M_values / N # 理論値
# シミュレーションによる確率計算
P_Xi_1_simulation = []
for M in M_values:
count_Xi_1 = 0
for _ in range(n_trials):
# 箱の中の球を準備(赤球 M 個、青球 N-M 個)
balls = [1] * M + [0] * (N - M)
# 1回の無作為抽出で赤球が引かれるかどうかを確認
drawn_ball = np.random.choice(balls)
if drawn_ball == 1:
count_Xi_1 += 1
# シミュレーション結果の確率
P_Xi_1_simulation.append(count_Xi_1 / n_trials)
# グラフに追加描画
plt.plot(M_values, P_Xi_1_theory, label=f'理論値 (N={N})', linestyle='--')
plt.plot(M_values, P_Xi_1_simulation, label=f'シミュレーション (N={N})', marker='o', linestyle='None')
# グラフのラベルとタイトル設定
plt.xlabel('赤球の数 (M)')
plt.ylabel('P(X_i = 1) の確率')
plt.title('異なる N における理論値とシミュレーション結果の比較')
plt.legend()
plt.grid(True)
plt.show()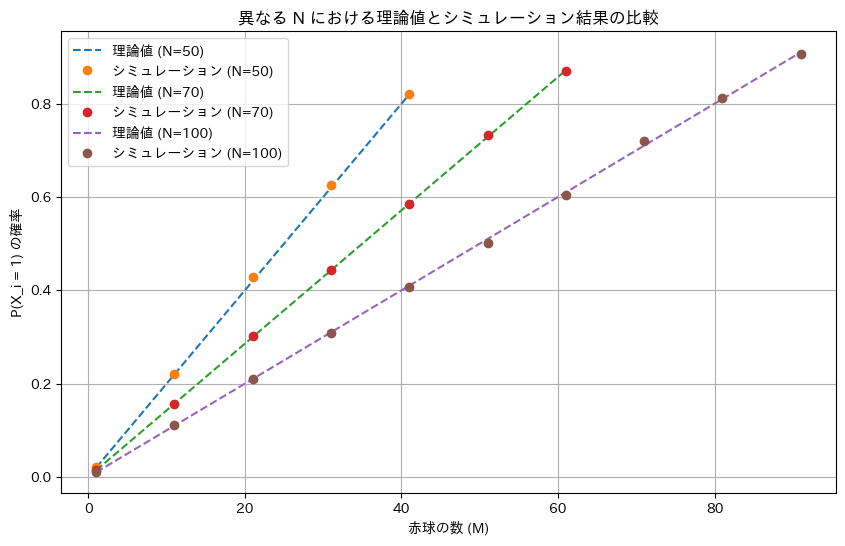
シミュレーションによる結果は理論値と一致しました。
2021 Q2(4)
事前分布と尤度から事後確率が最大となるパラメータの推定値を求めました。

コード
数式を使った計算
# 2021 Q2(4) 2024.8.24
import numpy as np
from scipy.special import comb
# 事前分布 P(N_A)
def prior(NA):
return NA + 1
# 尤度関数 P(X = 4 | N_A)
def likelihood(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# 事後分布 P(N_A | X = 4) (正規化定数は省略)
def posterior(NA):
return prior(NA) * likelihood(NA)
# N_A の範囲
NA_values = np.arange(4, 90)
# 事後分布の計算
posterior_values = [posterior(NA) for NA in NA_values]
# 最大値を取る N_A (事後モード) を探索
NA_mode = NA_values[np.argmax(posterior_values)]
NA_mode30プロット
# 2021 Q2(4) 2024.8.24
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
# 事前分布 P(N_A)
def prior(NA):
return NA + 1
# 正規化定数
C = 1 / 5151
# 尤度関数 P(X = 4 | N_A)
def likelihood(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# 事後分布 P(N_A | X = 4)
def posterior(NA):
return prior(NA) * likelihood(NA)
# N_A の範囲を0から100まで(事前分布用)
NA_values_full = np.arange(0, 101)
# 事前分布を計算(0から100まで)
prior_values_full = [C * prior(NA) for NA in NA_values_full]
# N_A の範囲を4から89まで(事後分布用)
NA_values = np.arange(4, 90)
# 事後分布の計算
posterior_values = [posterior(NA) for NA in NA_values]
# 事後分布の正規化
posterior_sum = sum(posterior_values)
posterior_values_normalized = [value / posterior_sum for value in posterior_values]
# 事前分布が存在しない場合の事後分布(尤度のみを正規化)
likelihood_values = [likelihood(NA) for NA in NA_values]
likelihood_sum = sum(likelihood_values)
likelihood_values_normalized = [value / likelihood_sum for value in likelihood_values]
# 3つの分布を重ねて表示
plt.figure(figsize=(10, 6))
# 事前分布のプロット(0から100まで)
plt.plot(NA_values_full, prior_values_full, 'g-', label=r'事前分布 $P(N_A)$', markersize=5)
# 事後分布のプロット(4から89まで)
plt.plot(NA_values, posterior_values_normalized, 'bo-', label=r'事後分布 $P(N_A | X = 4)$', markersize=5)
# 事前分布が存在しない場合の事後分布(尤度のみ)
plt.plot(NA_values, likelihood_values_normalized, 'r-', label=r'事前分布なし $P(N_A | X = 4)$', markersize=5)
# 事後モードのプロット
NA_mode = NA_values[np.argmax(posterior_values_normalized)]
plt.axvline(NA_mode, color='blue', linestyle='--', label=f'事後モード: {NA_mode}')
# 事前分布なしの場合の最尤推定値のプロット
NA_mode_likelihood = NA_values[np.argmax(likelihood_values_normalized)]
plt.axvline(NA_mode_likelihood, color='red', linestyle=':', label=f'最尤推定値 (事前分布なし): {NA_mode_likelihood}')
# グラフの設定
plt.xlabel(r'$N_A$')
plt.ylabel(r'確率')
plt.title(r'事前分布ありとなしの比較')
plt.grid(True)
plt.legend()
plt.show()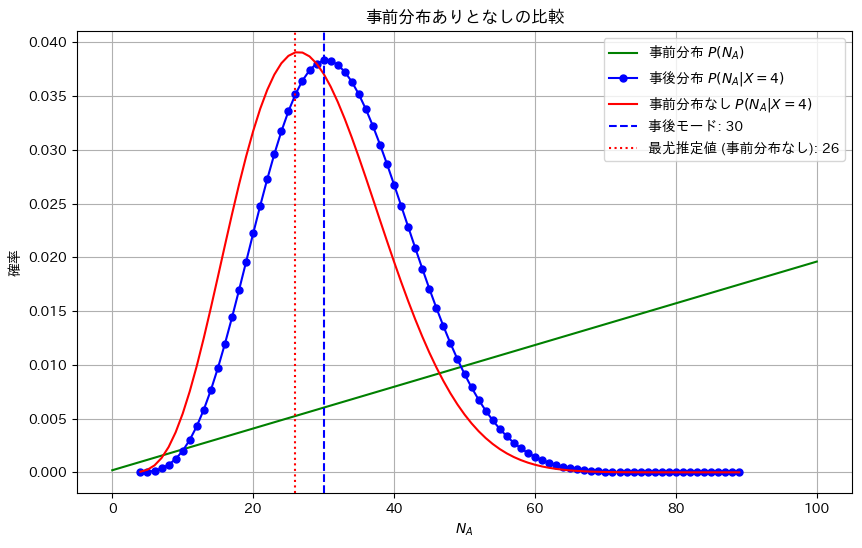
2021 Q2(2)
超幾何分布の当たりの数の推定値を尤度比を使って求めました。

コード
シミュレーションによる計算
# 2021 Q2(2) 2024.8.22
import numpy as np
from scipy.special import comb
# 尤度関数 L(N_A) を定義
def L(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# L(N_A + 1) / L(N_A) を計算し、条件を満たす最小の N_A を探索
# max(0, N_A - 85) ≤ 4 ≤ min(15, N_A) の式に基づき、取り出した豆Aが4粒の場合の N_A の範囲を設定 (4 ≤ N_A ≤ 89)
NA_values = np.arange(4, 90)
ratios = [(L(NA + 1) / L(NA)) for NA in NA_values]
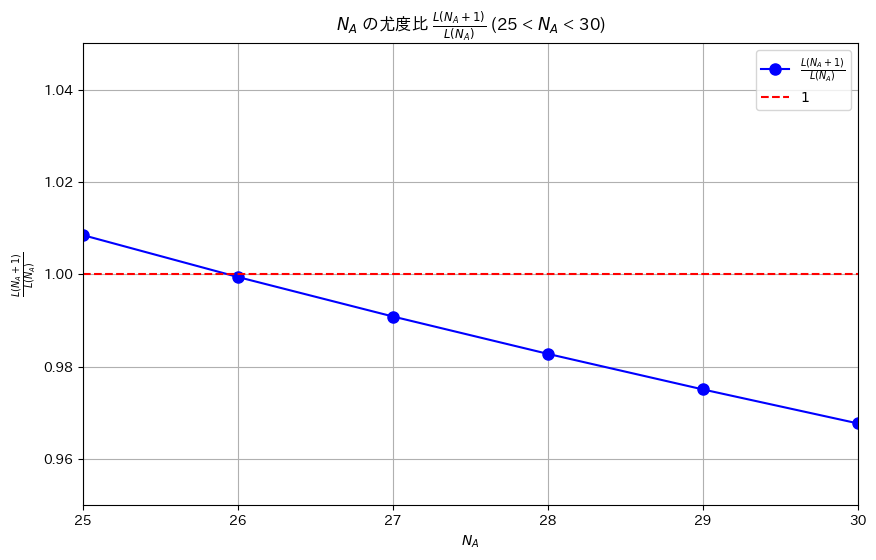
NA_optimal = NA_values[np.where(np.array(ratios) < 1)[0][0]]
print(f"L(N_A + 1) / L(N_A) < 1 となる最小の N_A は {NA_optimal} です。")
L(N_A + 1) / L(N_A) < 1 となる最小の N_A は 26 です。プロット
# 2021 Q2(2) 2024.8.22
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
# 尤度関数 L(N_A) を定義
def L(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# N_A の範囲を設定
NA_values = np.arange(4, 90)
ratios = [(L(NA + 1) / L(NA)) for NA in NA_values]
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(NA_values, ratios, 'bo-', label=r'$\frac{L(N_A + 1)}{L(N_A)}$', markersize=8)
plt.axhline(y=1, color='red', linestyle='--', label=r'$1$')
plt.xlabel(r'$N_A$')
plt.ylabel(r'$\frac{L(N_A + 1)}{L(N_A)}$')
plt.title(r'$N_A$ の尤度比 $\frac{L(N_A + 1)}{L(N_A)}$')
plt.legend()
plt.grid(True)
plt.show()
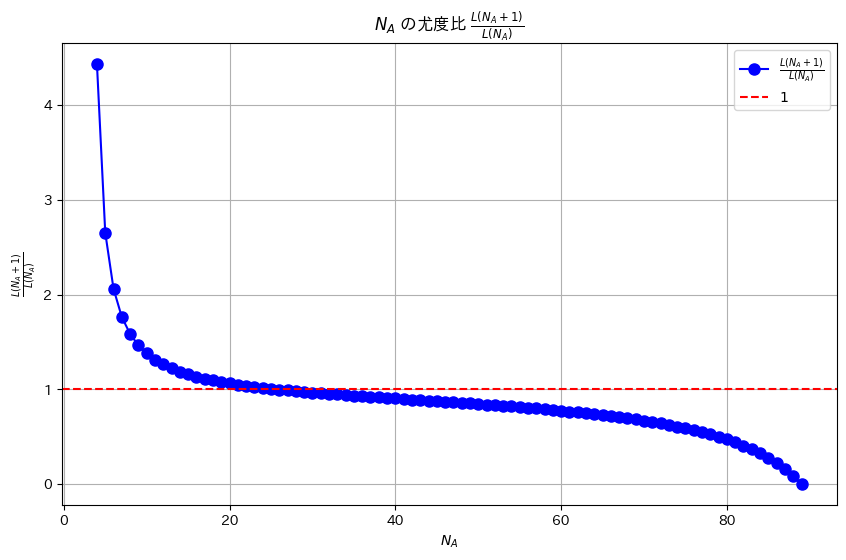
プロット(NA=26付近をズーム)
# 2021 Q2(2) 2024.8.22
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
# 尤度関数 L(N_A) を定義
def L(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# N_A の範囲を設定
NA_values = np.arange(4, 90)
ratios = [(L(NA + 1) / L(NA)) for NA in NA_values]
# 26付近のズームしたグラフを描画
plt.figure(figsize=(10, 6))
plt.plot(NA_values, ratios, 'bo-', label=r'$\frac{L(N_A + 1)}{L(N_A)}$', markersize=8)
plt.axhline(y=1, color='red', linestyle='--', label=r'$1$')
plt.xlabel(r'$N_A$')
plt.ylabel(r'$\frac{L(N_A + 1)}{L(N_A)}$')
plt.title(r'$N_A$ の尤度比 $\frac{L(N_A + 1)}{L(N_A)}$ (25 < $N_A$ < 30)')
plt.xlim(25, 30) # N_A = 26 付近をズーム
plt.ylim(0.95, 1.05) # y軸もズームして見やすく
plt.legend()
plt.grid(True)
plt.show()