2014 Q2(4)
n個の一様分布の順序統計量の同時分布が、前問の分布に等しい事を示しました。

コード
![]() と
と![]() の個別の分布をシミュレーションし、グラフを描画してみます。
の個別の分布をシミュレーションし、グラフを描画してみます。
# 2014 Q2(4) 2025.1.3
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 5 # 次元数
num_samples = 10000 # サンプル数
# (1) ガンマ分布からサンプルを生成して X_1, ..., X_(n+1) を計算
X = np.random.gamma(shape=1, scale=1, size=(num_samples, n+1)) # ガンマ分布からサンプル生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_(n+1)
# (2) Y_1, ..., Y_n を計算 (累積和を利用)
cumulative_sum_X = np.cumsum(X[:, :-1], axis=1) # 累積和 (X_1, X_1 + X_2, ..., X_1 + ... + X_n)
Y = cumulative_sum_X / T[:, None] # Y_i = (X_1 + ... + X_i) / T
# (3) 一様分布から順序統計量を生成
U = np.sort(np.random.uniform(0, 1, size=(num_samples, n)), axis=1) # 順序統計量 U_(1), ..., U_(n)
# (4) 個別の分布を比較
plt.figure(figsize=(12, 6))
for i in range(n):
plt.hist(Y[:, i], bins=50, alpha=0.5, density=True, label=rf"$Y_{i+1}$", histtype='step', linewidth=2)
plt.hist(U[:, i], bins=50, alpha=0.5, density=True, label=rf"$U_{{({i+1})}}$", histtype='step', linestyle='--', linewidth=2)
# グラフの装飾
plt.title("累積比率と順序統計量の個別分布の比較", fontsize=16)
plt.xlabel("値", fontsize=14)
plt.ylabel("確率密度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()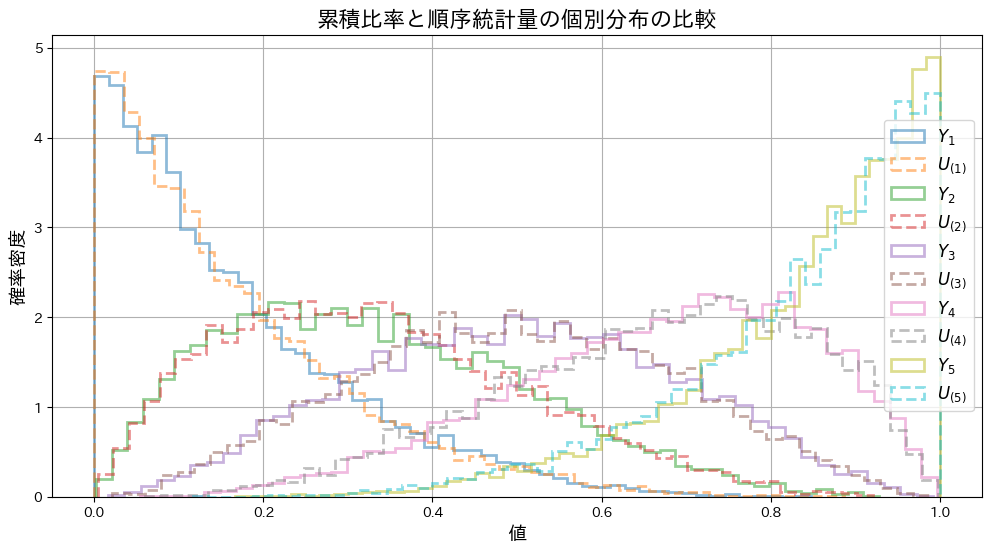
![]() と
と![]() の分布の形状は重なり、一致していることが確認できました。
の分布の形状は重なり、一致していることが確認できました。
次に、同時確率![]() と
と![]() の分布をシミュレーションし、グラフを描画してみます。
の分布をシミュレーションし、グラフを描画してみます。
# 2014 Q2(4) 2025.1.3
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 5 # 次元数
num_samples = 10000 # サンプル数
# (1) ガンマ分布からサンプルを生成して X_1, ..., X_(n+1) を計算
X = np.random.gamma(shape=1, scale=1, size=(num_samples, n+1)) # ガンマ分布からサンプル生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_(n+1)
# (2) Y_1, ..., Y_n を計算 (累積和を利用)
cumulative_sum_X = np.cumsum(X[:, :-1], axis=1) # 累積和 (X_1, X_1 + X_2, ..., X_1 + ... + X_n)
Y = cumulative_sum_X / T[:, None] # Y_i = (X_1 + ... + X_i) / T
# (3) 一様分布から順序統計量を生成
U = np.sort(np.random.uniform(0, 1, size=(num_samples, n)), axis=1) # 順序統計量 U_(1), ..., U_(n)
# (4) 同時確率密度を計算
cumulative_density = np.prod(Y, axis=1) # 累積比率 (Y_1 * Y_2 * ... * Y_n)
order_stats_density = np.prod(U, axis=1) # 順序統計量 (U_(1) * U_(2) * ... * U_(n))
# (5) ヒストグラムを描画して比較
plt.figure(figsize=(12, 6))
# 累積比率分布の同時確率密度
plt.hist(cumulative_density, bins=50, alpha=0.5, density=True, label=r"$f_Y(Y_1, Y_2, \ldots, Y_n)$")
# 順序統計量の同時確率密度
plt.hist(order_stats_density, bins=50, alpha=0.5, density=True, label=r"$f_U(U_{(1)}, U_{(2)}, \ldots, U_{(n)})$")
# グラフの装飾
plt.title("累積比率分布と順序統計量の同時確率密度の比較", fontsize=16)
plt.xlabel("同時確率密度", fontsize=14)
plt.ylabel("頻度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()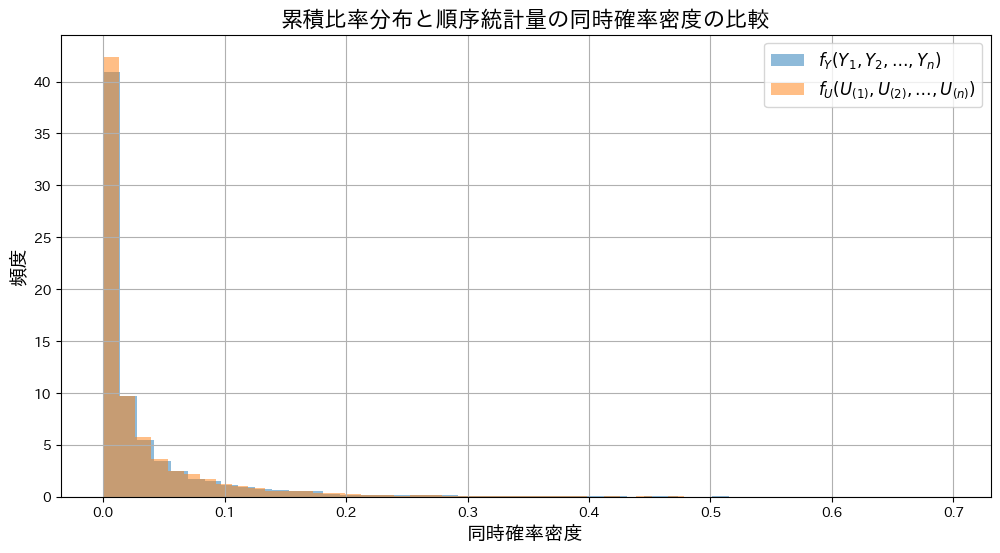
同時確率![]() と
と![]() の分布の形状は重なり、一致していることが確認できました。
の分布の形状は重なり、一致していることが確認できました。
2014 Q2(3)
形状パラメータが1のガンマ分布は指数分布となり、その和はガンマ分布に従うことを示しました。

コード
TとYの分布についてシミュレーションを行い、それらの形状を視覚化して確認します。
# 2014 Q2(3) 2024.1.2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
n = 5 # n+1 個のガンマ分布の和
num_samples = 10000 # シミュレーション回数
# ガンマ分布から乱数を生成
X = gamma.rvs(a=1, scale=1, size=(num_samples, n+1)) # 各行に n+1 個のガンマ乱数を生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_{n+1}
# 修正: Y を累積比率で計算
cumulative_sum_X = np.cumsum(X[:, :-1], axis=1) # X_1, X_1 + X_2, ..., X_1 + ... + X_n
Y = cumulative_sum_X / T[:, None] # Y_i = (X_1 + ... + X_i) / T
# T のヒストグラムを描画
plt.figure(figsize=(10, 6))
t_values = np.linspace(0, 30, 1000)
plt.hist(T, bins=50, density=True, alpha=0.6, color="blue", label="シミュレーション (T)")
plt.plot(t_values, gamma.pdf(t_values, a=n+1, scale=1), color="red", label=f"理論分布 (Gamma({n+1}, 1))")
plt.title("$T$ の分布", fontsize=16)
plt.xlabel("$T$", fontsize=14)
plt.ylabel("確率密度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()
# Y の確認 (サンプルの分布)
plt.figure(figsize=(10, 6))
for i in range(n):
plt.hist(Y[:, i], bins=50, density=True, alpha=0.5, label=f"$Y_{i+1}$")
plt.title("$Y$ の分布 (各比率)", fontsize=16)
plt.xlabel("$Y_i$", fontsize=14)
plt.ylabel("確率密度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()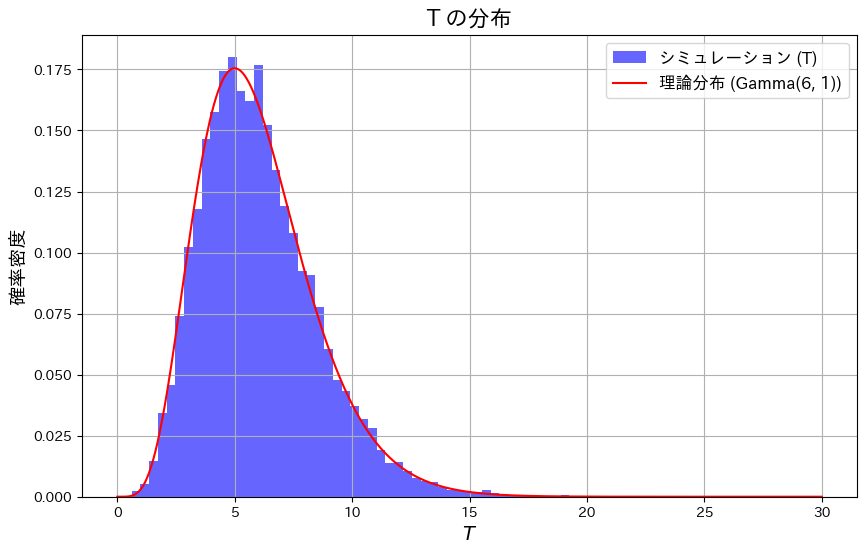
TがGa(n+1,1)のガンマ分布と一致することを確認しました。
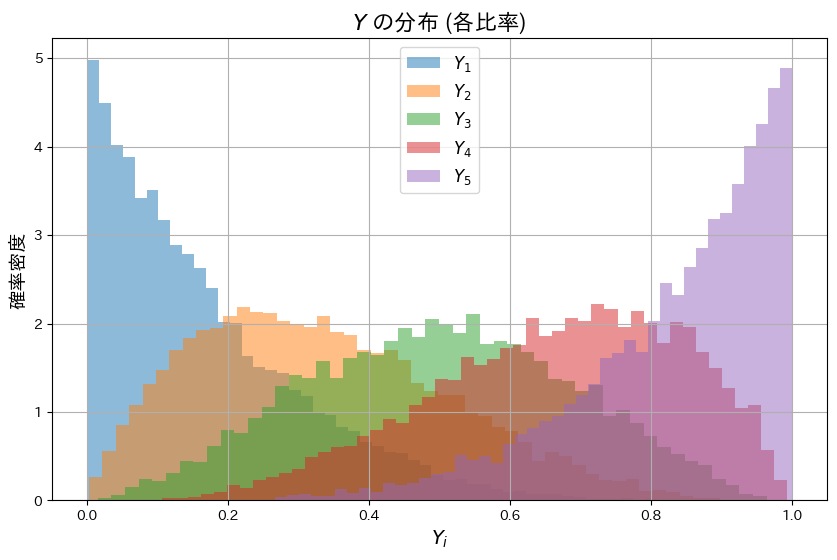
各Yiは累積比率として定義されているため、順序性(Y1<Y2<..<Yn)を持つように見えます。
次に、YiとTが独立であることを確認するため、散布図を描画し、それぞれの共分散Cov(Yi, T)を算出します。
# 2014 Q2(3) 2024.1.2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
n = 5 # n+1 個のガンマ分布の和
num_samples = 10000 # シミュレーション回数
# ガンマ分布から乱数を生成
X = gamma.rvs(a=1, scale=1, size=(num_samples, n+1)) # 各行に n+1 個のガンマ乱数を生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_{n+1}
Y = X[:, :-1] / T[:, None] # Y_i = X_i / T (最後の列を除いて正規化)
# (1) 共分散の計算
print("各 Y_i と T の共分散:")
for i in range(n):
cov = np.cov(Y[:, i], T)[0, 1] # 共分散行列から共分散を取得
print(f"Cov(Y_{i+1}, T) = {cov:.5f}")
# (2) 散布図の描画
plt.figure(figsize=(12, 8))
for i in range(n):
plt.scatter(T, Y[:, i], alpha=0.3, label=f"$Y_{i+1}$ vs $T$")
plt.title("散布図: 各 $Y_i$ と $T$ の関係", fontsize=16)
plt.xlabel("$T$", fontsize=14)
plt.ylabel("$Y_i$", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()各 Y_i と T の共分散:
Cov(Y_1, T) = 0.00426
Cov(Y_2, T) = 0.00394
Cov(Y_3, T) = -0.00261
Cov(Y_4, T) = -0.00364
Cov(Y_5, T) = -0.00399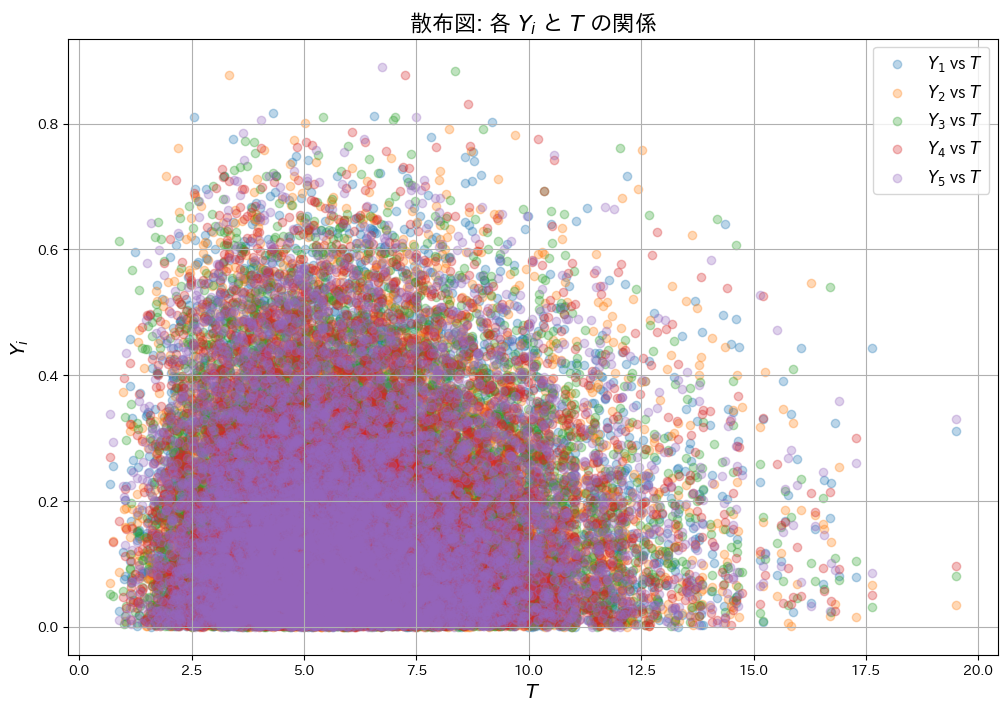
それぞれの共分散Cov(Yi, T)はほぼ0を示し、散布図からもYiとTが互いに影響を与えていないことが確認できました。
2016 Q2(4)
指数分布の上側確率の推定量が、ガンマ分布に従う確率変数の式で表され、それが不偏推定量であることを示しました。

コード
![]() はnによらず
はnによらず![]() に近づきます。nを1~20に変化させてシミュレーションして確認してみます。
に近づきます。nを1~20に変化させてシミュレーションして確認してみます。
# 2016 Q2(4) 2024.11.19
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
lambda_value = 2 # 固定されたλ
c = 1.0 # 定数c
n_values = range(1, 21) # nを1から20まで変化させる
sample_size = 1000 # シミュレーションのサンプルサイズ
simulated_expectations = [] # シミュレーション期待値を格納するリスト
theoretical_expectations = [] # 理論値を格納するリスト
# 修正版コード
for n in n_values:
# ガンマ分布のサンプルを生成 (Y ~ Gamma(n, λ))
Y_samples = np.random.gamma(shape=n, scale=1/lambda_value, size=sample_size)
# 条件付きで (1 - c/Y)^(n-1) を計算
values = np.where(Y_samples >= c, (1 - c / Y_samples)**(n - 1), 0)
# シミュレーション期待値を計算
simulated_expectations.append(np.mean(values))
# 理論値 e^(-λc) を計算
theoretical_expectations.append(np.exp(-lambda_value * c))
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(n_values, theoretical_expectations, 'r-o', label='理論値: e^(-λc)', linewidth=2)
plt.plot(n_values, simulated_expectations, 'b-s', label='シミュレーション期待値', linewidth=2)
# グラフの設定
plt.title('理論値とシミュレーション期待値の比較 (n を変化)', fontsize=16)
plt.xlabel('n (形状パラメータ)', fontsize=14)
plt.ylabel('期待値', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
# プロットの表示
plt.show()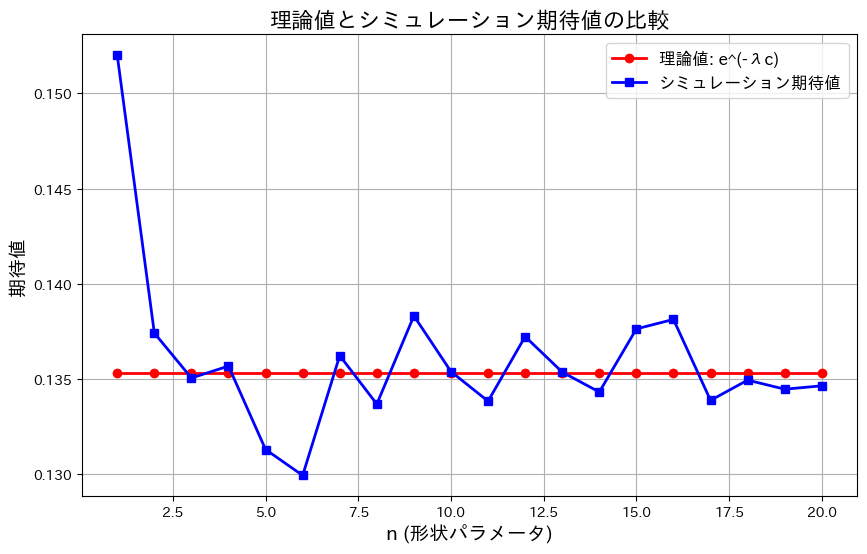
![]() はnによらず
はnによらず![]() に近づきました。グラフの縦軸の範囲が0.13~0.15と非常に狭いため、誤差が拡大して表示されているように見えます。実際の差異はごくわずかです。
に近づきました。グラフの縦軸の範囲が0.13~0.15と非常に狭いため、誤差が拡大して表示されているように見えます。実際の差異はごくわずかです。
2016 Q2(4)
指数分布の和がガンマ分布になることを示しました。

コード
指数分布に従う確率変数X1~Xnの和がガンマ分布に従うのをかを確かめるため、シミュレーションを行いました。この実験では、まずn=5の場合について確かめました。
# 2016 Q2(4) 2024.11.18
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # 真のλ
n = 5 # 指数分布の和の数 (ガンマ分布の形状パラメータ)
sample_size = 10000 # シミュレーションのサンプルサイズ
# 1. 指数分布の和をシミュレーション
sum_of_exponentials = np.sum(np.random.exponential(scale=1/lambda_value, size=(sample_size, n)), axis=1)
# 2. ガンマ分布の理論値を計算
x = np.linspace(0, max(sum_of_exponentials), 1000)
gamma_pdf = gamma.pdf(x, a=n, scale=1/lambda_value)
# 3. ヒストグラムと理論的なガンマ分布をプロット
plt.figure(figsize=(10, 6))
plt.hist(sum_of_exponentials, bins=50, density=True, alpha=0.6, color='skyblue', label='シミュレーション (指数分布の和)')
plt.plot(x, gamma_pdf, 'r-', label='理論的なガンマ分布', linewidth=2)
# グラフの設定
plt.title('指数分布の和 (n=5) とガンマ分布の比較', fontsize=16)
plt.xlabel('値', fontsize=14)
plt.ylabel('密度', fontsize=14)
plt.legend(fontsize=12)
plt.grid(True)
# プロット表示
plt.show()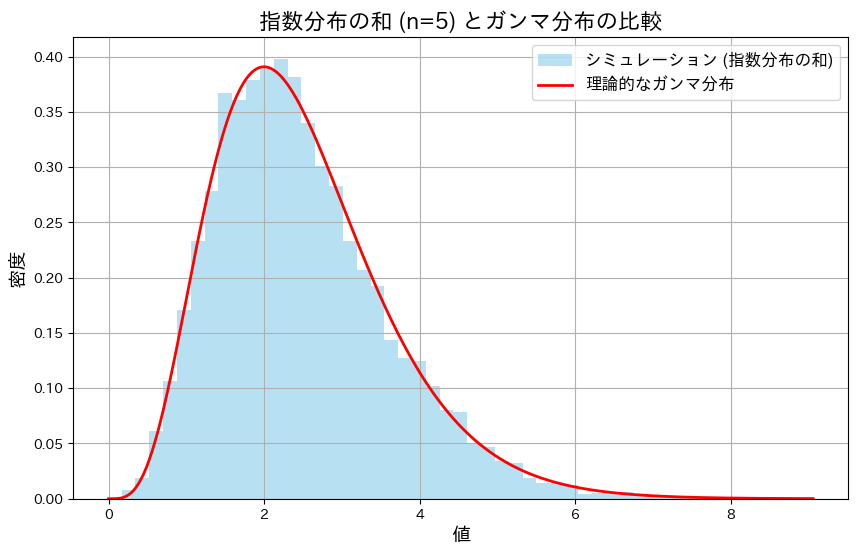
5つの指数分布の和は、形状パラメータが5のガンマ分布に一致することが確認できました。
次に、nを変化させてシミュレーションを行い、分布の形状の変化を観察します。また、それらの分布がガンマ分布と一致するかを確認します。
# 2016 Q2(4) 2024.11.18
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # 真のλ
n_values = [2, 5, 10, 20] # nの値を変化させる
sample_size = 10000 # シミュレーションのサンプルサイズ
# 2x2のグリッドでプロット
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.flatten()
for i, n in enumerate(n_values):
# 指数分布の和をシミュレーション
sum_of_exponentials = np.sum(np.random.exponential(scale=1/lambda_value, size=(sample_size, n)), axis=1)
# ガンマ分布の理論値を計算
x = np.linspace(0, 20, 1000) # 横軸の範囲を0~20に設定
gamma_pdf = gamma.pdf(x, a=n, scale=1/lambda_value)
# ヒストグラムと理論的なガンマ分布をプロット
ax = axes[i]
ax.hist(sum_of_exponentials, bins=50, range=(0, 20), density=True, alpha=0.6, color='skyblue', label='シミュレーション (指数分布の和)')
ax.plot(x, gamma_pdf, 'r-', label='理論的なガンマ分布', linewidth=2)
# グラフの設定
ax.set_title(f'n={n}', fontsize=14)
ax.set_xlabel('値', fontsize=12)
ax.set_ylabel('密度', fontsize=12)
ax.legend(fontsize=10)
ax.grid(True)
# 全体のレイアウト調整
plt.suptitle('nを変化させた指数分布の和とガンマ分布の比較', fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.show()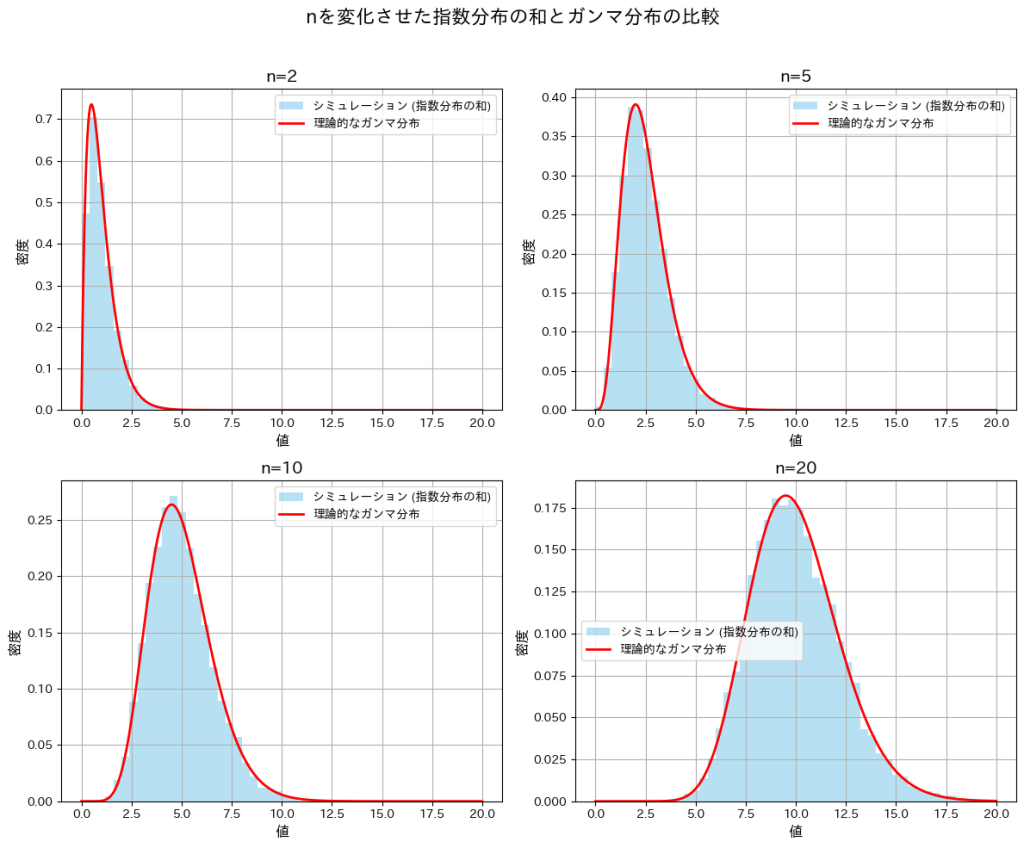
nが小さいときは分布が右に裾が長くなり、nが大きくなるにつれて左右対称に近づいています。また、どのnにおいても形状パラメータnのガンマ分布とよく一致していることが確認できました。
2019 Q2(3)
(2)で求めた確率密度関数において確率変数Uの逆数の期待値を求めました。
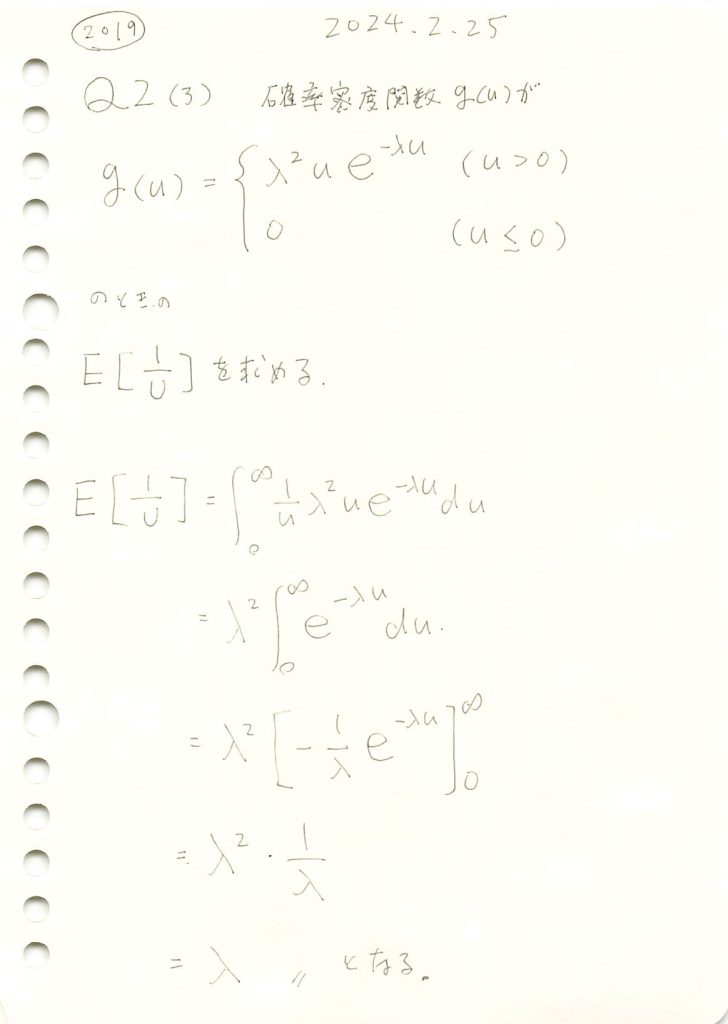
コード
数式を使って1/Uの期待値を求めます。
# 2019 Q2(3) 2024.9.15
import sympy as sp
# 変数の定義
u, lambda_value = sp.symbols('u lambda', positive=True, real=True)
# ガンマ分布の確率密度関数 g(u) = λ^2 * u * exp(-λ * u)
g_u = lambda_value**2 * u * sp.exp(-lambda_value * u)
# 1/U の期待値の積分
integrand = (1/u) * g_u # 1/u * g(u)
# 積分の実行
expectation = sp.integrate(integrand, (u, 0, sp.oo))
# 結果の簡略化
expectation_simplified = sp.simplify(expectation)
# 結果の表示
display(expectation_simplified)手計算と一致します。
次に、数値シミュレーションを行います。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
lambda_value = 2 # λ=2
num_samples = 100000 # サンプルの数
# 指数分布に従う乱数 X1, X2 を生成
X1 = np.random.exponential(scale=1/lambda_value, size=num_samples)
X2 = np.random.exponential(scale=1/lambda_value, size=num_samples)
# U = X1 + X2 の計算
U = X1 + X2
# 1/U の計算
inv_U = 1 / U
# シミュレーションの結果からの平均値
simulation_result = np.mean(inv_U)
# 理論値 E[1/U] = λ
theoretical_value = lambda_value
# 結果の表示
print(f'シミュレーションによる E[1/U]: {simulation_result}')
print(f'理論値 E[1/U]: {theoretical_value}')
# ヒストグラムの描画
plt.hist(inv_U, bins=50, density=True, alpha=0.7, label='シミュレーション結果')
plt.axvline(theoretical_value, color='r', linestyle='--', label=f'理論値 E[1/U] = {theoretical_value}')
plt.xlabel('1/U')
plt.ylabel('確率密度')
plt.title('シミュレーションによる 1/U の分布と理論値の比較')
plt.legend()
plt.show()シミュレーションによる E[1/U]: 1.9928303711222939
理論値 E[1/U]: 2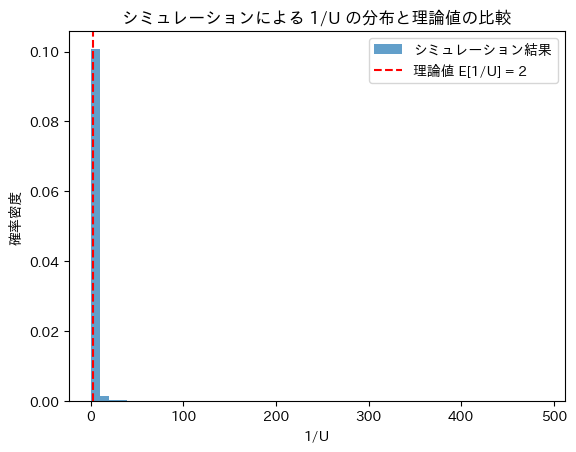
シミュレーションによりE[1/U]は理論値に近づきました。分散は発散するためヒストグラムにすると大きなバラつきが見られます。
2019 Q2(2)
独立な指数分布に従う2変数の和の確率密度関数を求めました。

コード
数式を使ってUの確率密度関数を求めます。
# 2019 Q2(2) 2024.9.14
import sympy as sp
# 変数の定義
x, u, lambda_value = sp.symbols('x u lambda', positive=True, real=True)
# 指数分布の確率密度関数 (PDF) f(x)
f_x = lambda_value * sp.exp(-lambda_value * x)
# 畳み込み積分を計算して、g(u) = f(x) * f(u - x) の形式にする
g_u = sp.integrate(f_x * lambda_value * sp.exp(-lambda_value * (u - x)), (x, 0, u))
# 簡略化
g_u_simplified = sp.simplify(g_u)
# 結果の表示
display(g_u_simplified)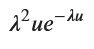
X1 (X2)と、Uの確率密度関数を重ねて描画してみます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # λ=2
x_range = np.linspace(0, 5, 1000) # X1, X2 の範囲
# X1, X2 の指数分布の確率密度関数 (PDF) - 同じなので1つにまとめる
pdf_X1_X2 = lambda_value * np.exp(-lambda_value * x_range)
# U = X1 + X2 は形状パラメータk=2、スケールパラメータθ=1/λのガンマ分布
u_range = np.linspace(0, 10, 1000)
pdf_U = gamma.pdf(u_range, a=2, scale=1/lambda_value)
# グラフのプロット
plt.figure(figsize=(8, 6))
# X1 (X2) の指数分布の描画
plt.plot(x_range, pdf_X1_X2, label='X1 (X2) (指数分布)', color='blue', linestyle='--')
# U のガンマ分布の描画
plt.plot(u_range, pdf_U, label='U = X1 + X2 (ガンマ分布)', color='red')
# グラフの装飾
plt.title('X1 (X2) と U の確率密度関数の比較')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.show()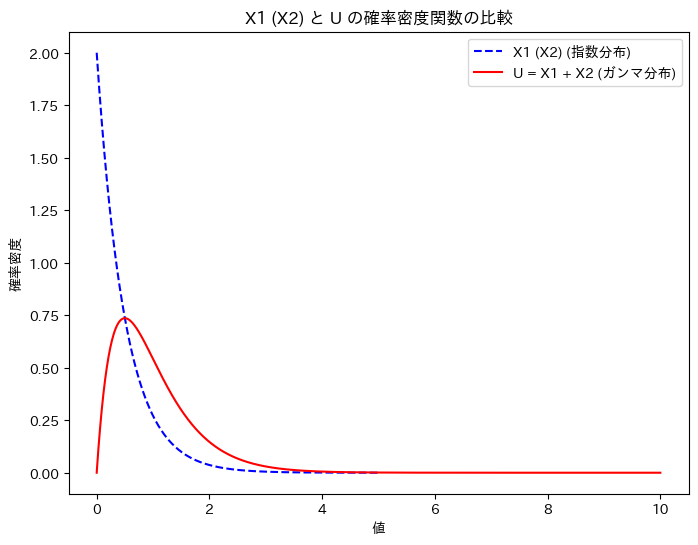
グラフの形状から、U = X1 + X2の関係は想像しづらいですね。
ガンマ分布の形状パラメータを1~2に変化させて、X1 (X2)からUへの変化を確認します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # λ=2
x_range = np.linspace(0, 5, 1000) # X1, X2, U の範囲を0~5に設定
# ガンマ分布の形状パラメータを1から2まで0.1ずつ変化させる
shape_params = np.arange(1, 2.1, 0.1) # 1から2までの形状パラメータを0.1ステップで変化
# グラフのプロット
plt.figure(figsize=(8, 6))
# 形状パラメータが1から2に変化するガンマ分布の描画
for k in shape_params:
gamma_pdf = gamma.pdf(x_range, a=k, scale=1/lambda_value)
plt.plot(x_range, gamma_pdf, label=f'形状パラメータ k={k:.1f}')
# X1 (X2) の指数分布の描画 - 同じなので1つにまとめる
pdf_X1_X2 = lambda_value * np.exp(-lambda_value * x_range)
plt.plot(x_range, pdf_X1_X2, label='X1 (X2) (指数分布)', color='blue', linestyle='--')
# グラフの装飾
plt.title('指数分布からガンマ分布への変化 (形状パラメータの0.1ステップ変化)')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.show()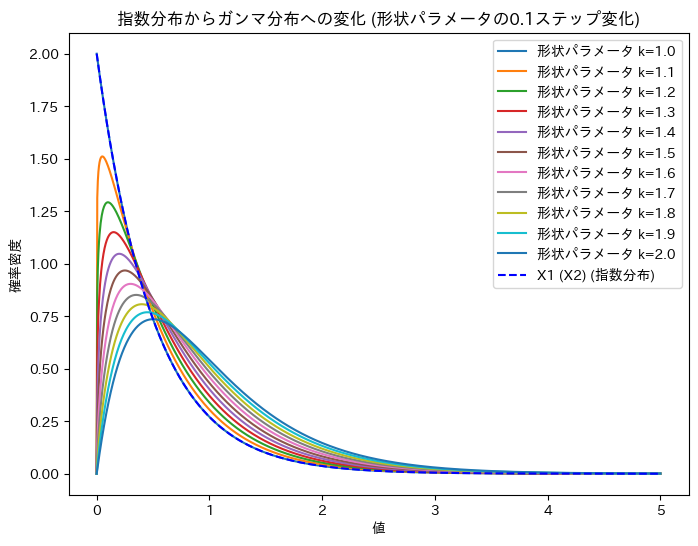
X1 (X2)からUへの変化が可視化できました。
次に、X1 (X2)と、Uの累積分布関数を重ねて描画してみます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon, gamma
# パラメータ設定
lambda_value = 2 # λ=2
x_range = np.linspace(0, 5, 1000) # X1, X2 の範囲
# X1, X2 の指数分布の累積分布関数 (CDF) - 同じなので1つにまとめる
cdf_X1_X2 = expon.cdf(x_range, scale=1/lambda_value)
# U = X1 + X2 は形状パラメータk=2、スケールパラメータθ=1/λのガンマ分布
u_range = np.linspace(0, 10, 1000)
cdf_U = gamma.cdf(u_range, a=2, scale=1/lambda_value)
# グラフのプロット
plt.figure(figsize=(8, 6))
# X1 (X2) の指数分布のCDFの描画
plt.plot(x_range, cdf_X1_X2, label='X1 (X2) (指数分布 CDF)', color='blue', linestyle='--')
# U のガンマ分布のCDFの描画
plt.plot(u_range, cdf_U, label='U = X1 + X2 (ガンマ分布 CDF)', color='red')
# グラフの装飾
plt.title('X1 (X2) と U の累積分布関数 (CDF) の比較')
plt.xlabel('値')
plt.ylabel('累積確率')
plt.legend()
# グラフの表示
plt.show()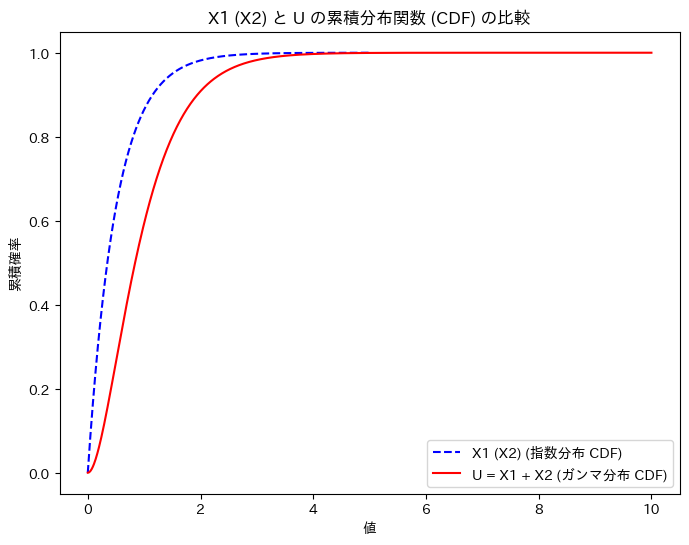
グラフの形状から、U = X1 + X2の関係を想像しやすくなりました。
2019 Q2(1)
独立な指数分布に従う2変数の和の期待値を求めました。
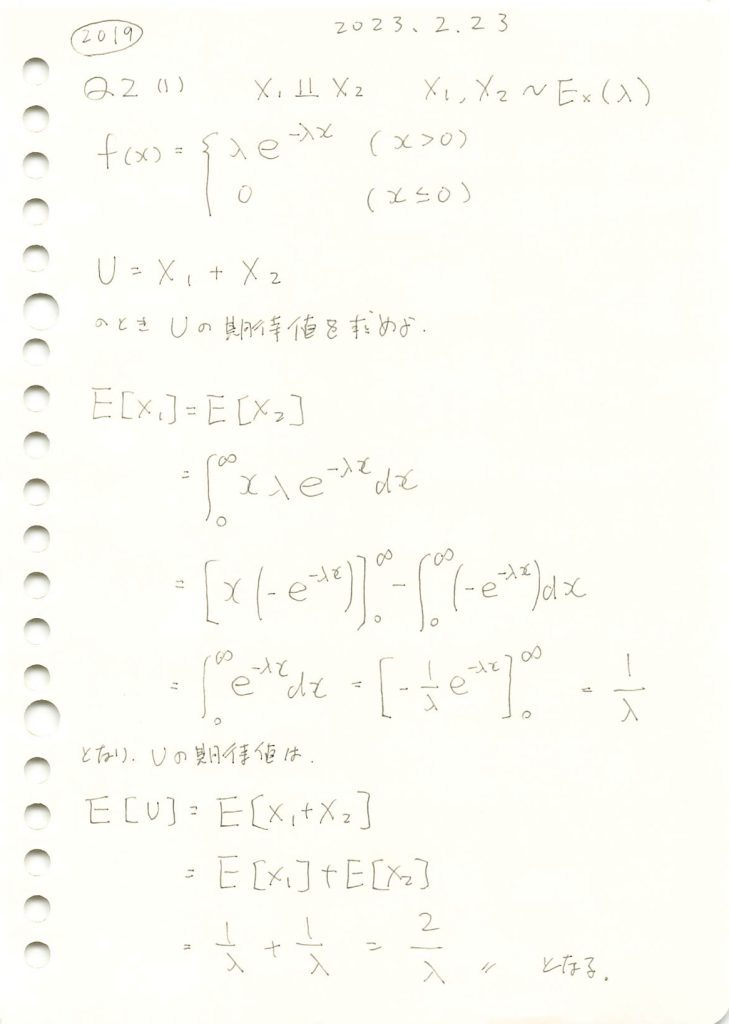
コード
数式を使ってUの期待値を求めます
import sympy as sp
# 変数の定義
x = sp.Symbol('x', positive=True)
lambda_value = sp.Symbol('lambda', positive=True)
# 指数分布の確率密度関数 (PDF)
f_x = lambda_value * sp.exp(-lambda_value * x)
# 期待値の式を計算 (積分)
E_X1 = sp.integrate(x * f_x, (x, 0, sp.oo))
# 期待値
E_X1_simplified = sp.simplify(E_X1)
# X1 + X2 の場合 (独立性より)
E_U = 2 * E_X1_simplified
# 結果の表示
display(E_U)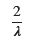
手計算と一致します
次にUに従う乱数を生成し分布を確認します。また形状パラメータ2のガンマ分布と重ねて描画します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # 例としてλ=2
num_samples = 1000 # サンプルの数
# 指数分布に従う乱数の生成
X1 = np.random.exponential(scale=1/lambda_value, size=num_samples)
X2 = np.random.exponential(scale=1/lambda_value, size=num_samples)
# U = X1 + X2 の計算
U = X1 + X2
# 理論的な期待値
expected_value = 2 / lambda_value
# シミュレーション結果のヒストグラムのプロット (確率密度にスケール)
plt.hist(U, bins=30, density=True, alpha=0.7, label='シミュレーション結果')
# ガンマ分布 (形状パラメータ k=2, スケールパラメータ θ=1/λ) の確率密度関数 (PDF) を計算
k = 2 # 形状パラメータ (k = 2)
theta = 1 / lambda_value # スケールパラメータ (θ = 1/λ)
# ガンマ分布に基づくx軸の範囲
x = np.linspace(0, max(U), 1000)
# ガンマ分布の確率密度関数 (PDF) を計算
gamma_pdf = gamma.pdf(x, a=k, scale=theta)
# ガンマ分布の折れ線グラフをプロット
plt.plot(x, gamma_pdf, 'r-', label=f'ガンマ分布 (k={k}, θ={theta:.2f})')
# グラフの装飾
plt.axvline(expected_value, color='g', linestyle='--', label=f'理論値 = {expected_value:.2f}')
plt.xlabel('U = X1 + X2')
plt.ylabel('確率密度')
plt.title('Uの分布とガンマ分布の比較')
plt.legend()
plt.show()
# 実際のサンプル平均値と理論的期待値の比較
print(f'理論的な期待値: {expected_value}')
print(f'シミュレーションからの平均値: {np.mean(U)}')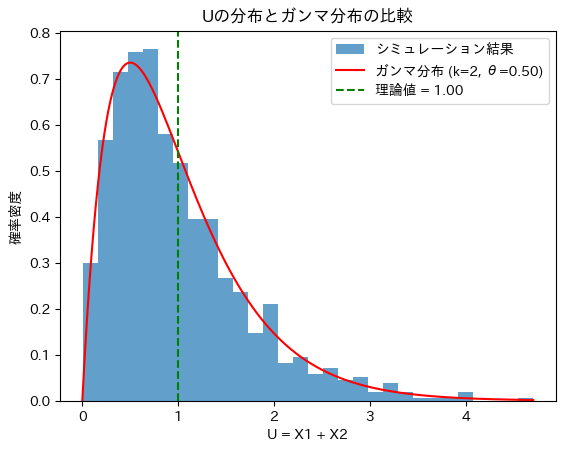
理論的な期待値: 1.0
シミュレーションからの平均値: 0.9902440726761544Uの分布と形状パラメータ2のガンマ分布は重なりました。Uはガンマ分布に従うことが分かります。
2022 Q3(5)
モーメント法によりガンマポアソン分布のパラメータの推定量を求めました。

コード
数式を使った計算
# 2022 Q3(5) 2024.8.6
from sympy import init_printing
from sympy import symbols, Eq, solve
# これでTexの表示ができる
init_printing()
# 変数の定義
r, p, X_bar, S_squared = symbols('r p X_bar S_squared')
alpha, beta = symbols('alpha beta')
# モーメント法の方程式を定義
# 期待値 E[X] にサンプル平均を一致させる
eq1_correct = Eq(X_bar, alpha / beta)
# 分散 V[X] にサンプル分散を一致させる
eq2_correct = Eq(S_squared, alpha / beta**2 + alpha / beta)
# 方程式を解いて α と β を求める
solutions_correct = solve((eq1_correct, eq2_correct), (alpha, beta))
solutions_correct
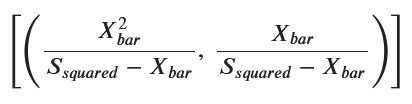
シミュレーションによる計算
# 2022 Q3(5) 2024.8.6
import numpy as np
from scipy.stats import nbinom
# 1. パラメータの設定
alpha_true = 3.0
beta_true = 2.0
# 2. 負の二項分布のパラメータ計算
r = alpha_true
p = beta_true / (beta_true + 1)
# 3. 負の二項分布から乱数を生成
sample_size = 10000
nbinom_samples = nbinom.rvs(r, p, size=sample_size)
# 4. サンプル統計量の計算
X_bar = np.mean(nbinom_samples)
S_squared = np.var(nbinom_samples, ddof=1)
# 5. モーメント法によるパラメータ推定
alpha_estimated = X_bar**2 / (S_squared - X_bar)
beta_estimated = X_bar / (S_squared - X_bar)
# 6. 推定結果の表示
print(f"推定された α: {alpha_estimated}")
print(f"推定された β: {beta_estimated}")
print(f"理論値 α: {alpha_true}")
print(f"理論値 β: {beta_true}")推定された α: 2.93536458612626
推定された β: 1.95157541794180
理論値 α: 3.0
理論値 β: 2.0アルゴリズム
シミュレーションによる計算
パラメータの設定:
- 真のパラメータ
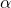 と
と 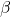 を設定する。
を設定する。
負の二項分布のパラメータ計算:
- パラメータ

- パラメータ
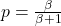
負の二項分布から乱数を生成:
- サンプルサイズ
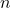 を設定し、負の二項分布から乱数を生成する。
を設定し、負の二項分布から乱数を生成する。
サンプル統計量の計算:
- サンプル平均
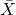 と分散
と分散 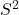 を計算する。
を計算する。
モーメント法によるパラメータ推定:
- 推定された
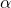 を
を 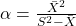 で計算する。
で計算する。 - 推定された
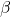 を
を 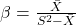 で計算する。
で計算する。
推定結果の表示:
- 推定された
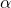 と
と 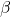 を表示する。
を表示する。 - 真の
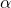 と
と 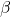 を表示する。
を表示する。