2017 Q5(3)
独立した二つの自由度1のカイ二乗分布の差を幾何平均と2でスケールした式の確率密度関数を導出しました。

コード
Tについてシミュレーションし、確率密度関数![]() と一致するか確認をします。
と一致するか確認をします。
# 2017 Q5(3) 2024.11.10
import numpy as np
import matplotlib.pyplot as plt
# サンプルサイズ
n_samples = 100000
# 自由度1のカイ二乗分布からサンプルを生成
X = np.random.chisquare(df=1, size=n_samples)
Y = np.random.chisquare(df=1, size=n_samples)
# 確率変数 T = (X - Y) / (2 * sqrt(X * Y)) の計算
T = (X - Y) / (2 * np.sqrt(X * Y))
# 理論的な確率密度関数 h(t) の定義
def theoretical_h(t):
return 1 / (np.pi * (1 + t**2))
# x 軸の範囲を設定し、h(t) を計算
x = np.linspace(-10, 10, 100)
h_t = theoretical_h(x)
# グラフの描画
plt.hist(T, bins=200, density=True, alpha=0.5, range=(-10, 10), label='シミュレーションによる $T$')
plt.plot(x, h_t, 'r-', label='理論的な $h(t) = \\frac{1}{\\pi(1+t^2)}$')
plt.xlabel('$T$')
plt.ylabel('密度')
plt.legend()
plt.title('確率変数 $T$ のシミュレーションと理論密度関数')
plt.show()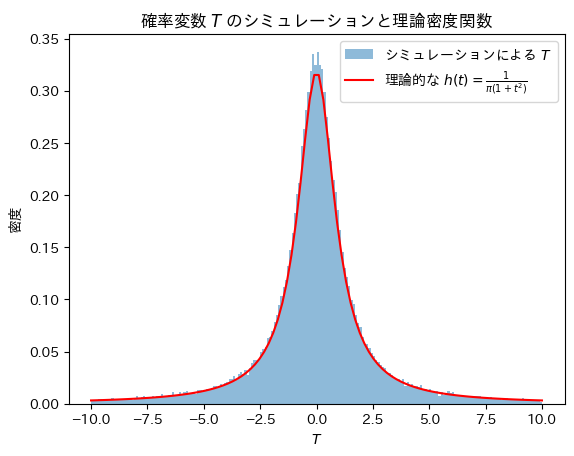
Tの分布は確率密度関数![]() と一致することが確認できました。
と一致することが確認できました。
なお、Tの分布は標準コーシー分布と呼ばれます。
2019 Q4(4)
コーシー分布の検定で、与えられた棄却域が最強力検定になることを示しました。
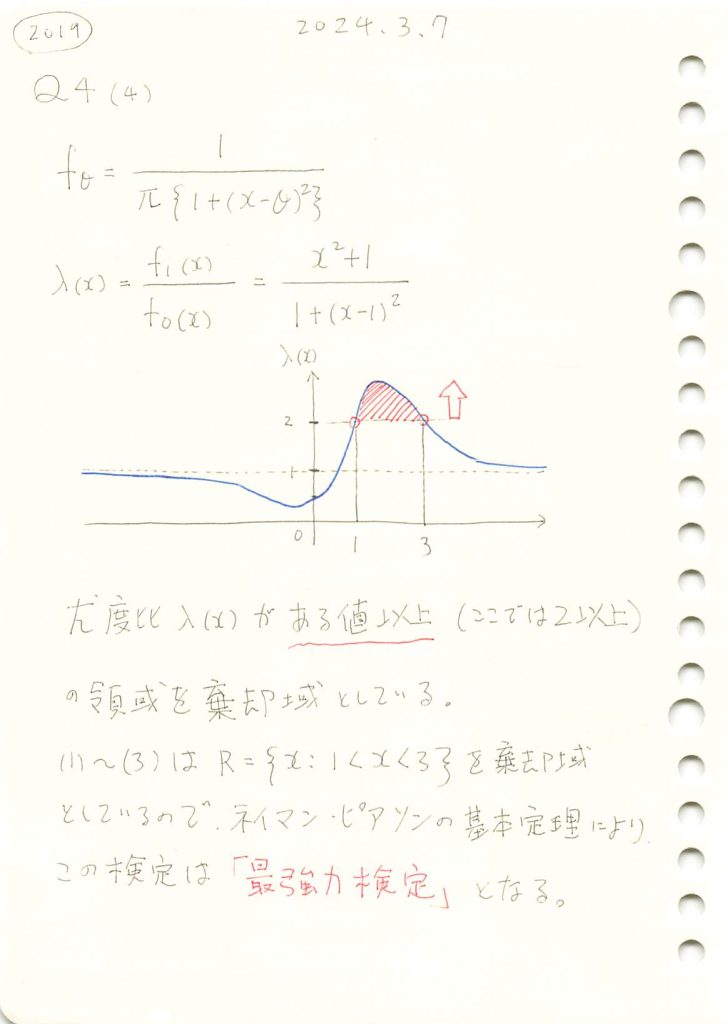
コード
棄却域をR={x:1<x<3}にする検定が最強力検定になるのか確認するために、尤度比λ(x)のグラフを描画します。
# 2019 Q4(4) 2024.9.26
import numpy as np
import matplotlib.pyplot as plt
# 尤度比 λ(x) の計算
def likelihood_ratio(x):
return (1 + x**2) / (1 + (x - 1)**2)
# x の範囲を設定
x_values = np.linspace(-5, 5, 500)
# λ(x) の値を計算
lambda_values = likelihood_ratio(x_values)
# グラフを描画
plt.figure(figsize=(10, 6))
plt.plot(x_values, lambda_values, label=r'尤度比 $\lambda(x) = \frac{1 + x^2}{1 + (x - 1)^2}$', color='b')
# 棄却域 1 < x < 3 を塗りつぶす(透明度を追加)
plt.axvspan(1, 3, color='yellow', alpha=0.3, label=r'棄却域 $1 < x < 3$')
# λ(x) >= 2 の部分を赤で塗る
plt.fill_between(x_values, lambda_values, 2, where=(lambda_values >= 2), color='red', alpha=0.3, label=r'$\lambda(x) \geq 2$')
# グラフの装飾
plt.axhline(2, color='green', linestyle='--', label=r'閾値 $\lambda(x) = 2$')
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title(r'尤度比 $\lambda(x)$ と棄却域 $1 < x < 3$, $\lambda(x) \geq 2$ の範囲')
plt.xlabel('x')
plt.ylabel(r'$\lambda(x)$')
plt.grid(True)
plt.legend()
# グラフを表示
plt.show()
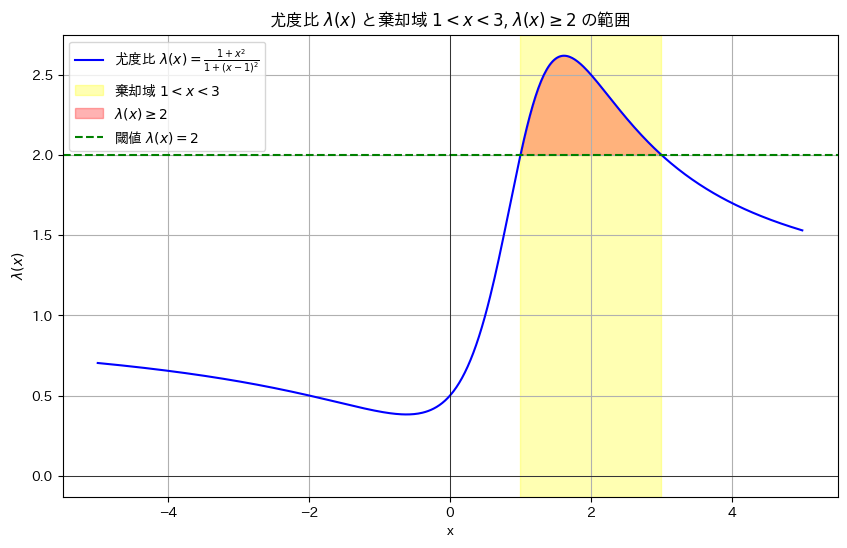
棄却域は尤度比λ(x)>c (ここではc=2)で定義できるので、これは最強力検定と言えます。
ところでx->-∞で尤度比λ(x)はどこに収束するのでしょうか。
import numpy as np
import matplotlib.pyplot as plt
# 尤度比 λ(x) の計算
def likelihood_ratio(x):
return (1 + x**2) / (1 + (x - 1)**2)
# x の範囲を設定(左側を広げる)
x_values = np.linspace(-50, 5, 500)
# λ(x) の値を計算
lambda_values = likelihood_ratio(x_values)
# グラフを描画
plt.figure(figsize=(10, 6))
plt.plot(x_values, lambda_values, label=r'尤度比 $\lambda(x) = \frac{1 + x^2}{1 + (x - 1)^2}$', color='b')
# 閾値を視覚化
plt.axhline(1, color='purple', linestyle='--', label=r'極限 $\lambda(x) \to 1$ as $x \to -\infty$')
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title(r'尤度比 $\lambda(x)$ の概形 ($x \to -\infty$ の範囲)')
plt.xlabel('x')
plt.ylabel(r'$\lambda(x)$')
plt.grid(True)
plt.legend()
# グラフを表示
plt.show()
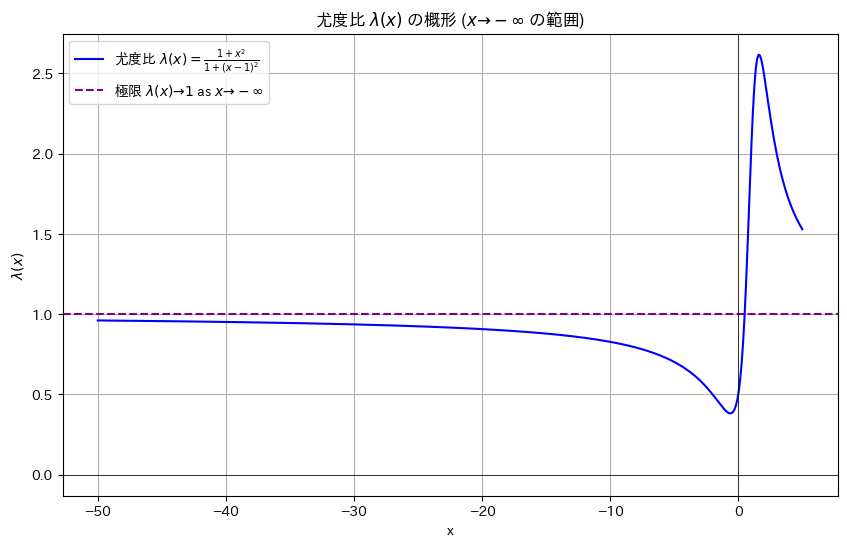
1.0に収束するようです。
よって、cは1以上で、且つ尤度比λ(x)が最大となるx = 1.61803398874989(黄金比)が棄却域に含まれていれば最強力検定になります。
2019 Q4(3)
コーシー分布のパラメータ違いの尤度比の概形を描きました。
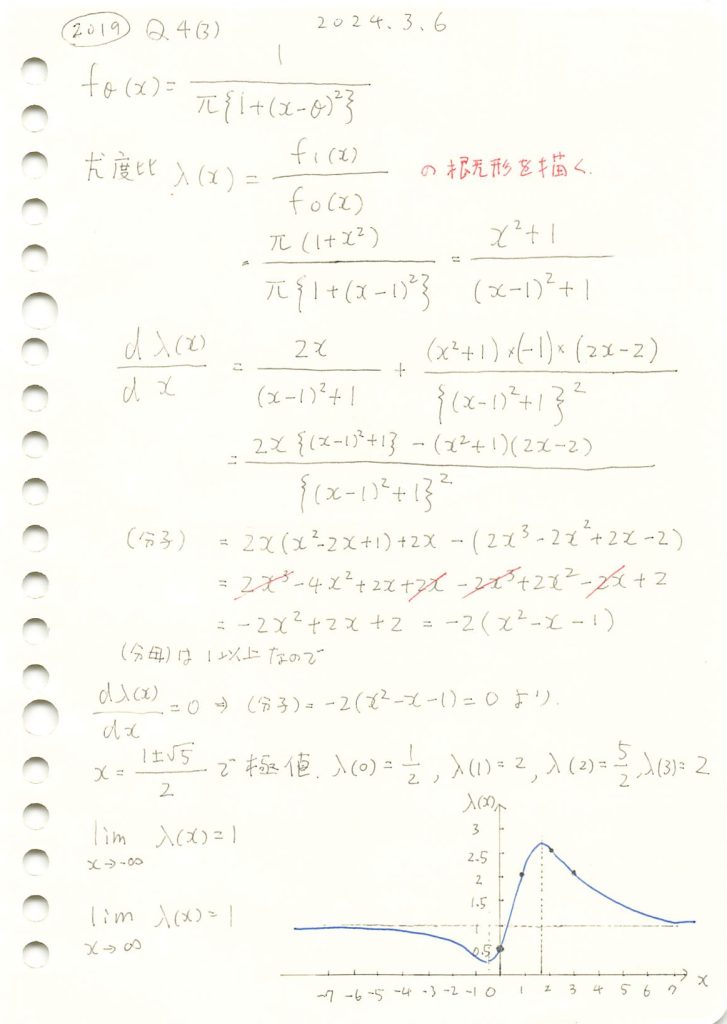
コード
尤度比λ(x)のグラフを描画します。
# 2019 Q4(3) 2024.9.25
import numpy as np
import matplotlib.pyplot as plt
# 尤度比 λ(x) の計算
def likelihood_ratio(x):
return (1 + x**2) / (1 + (x - 1)**2)
# x の範囲を設定
x_values = np.linspace(-5, 5, 500)
# λ(x) の値を計算
lambda_values = likelihood_ratio(x_values)
# グラフを描画
plt.figure(figsize=(10, 6))
plt.plot(x_values, lambda_values, label=r'尤度比 $\lambda(x) = \frac{1 + x^2}{1 + (x - 1)^2}$', color='b')
plt.scatter([1, 3], [2, 2], color='red', zorder=5) # x = 1 および x = 3 の点をプロット
# グラフの装飾
plt.axhline(0, color='black',linewidth=0.5)
plt.axvline(0, color='black',linewidth=0.5)
plt.title(r'尤度比 $\lambda(x)$ の概形')
plt.xlabel('x')
plt.ylabel(r'$\lambda(x)$')
plt.grid(True)
plt.legend()
# グラフを表示
plt.show()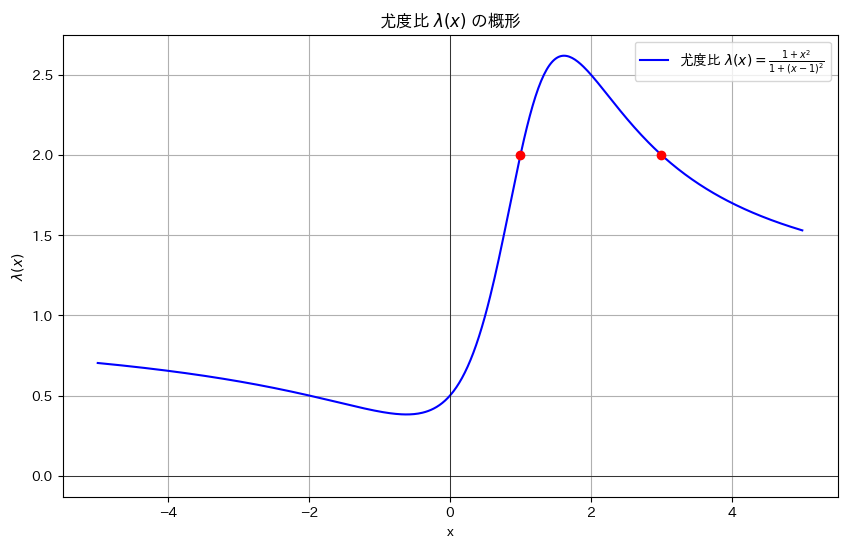
谷と山を持つ形状をしています。
次に、尤度関数λ(x)の1次導関数と2次導関数から、極値と形状(山か谷か)を導きます。
# 2019 Q4(3) 2024.9.25
import sympy as sp
from IPython.display import display
# 尤度比 λ(x) の式を定義
x = sp.symbols('x')
lambda_x = (1 + x**2) / (1 + (x - 1)**2)
# 1次導関数を計算
lambda_prime = sp.diff(lambda_x, x)
print("1次導関数 λ'(x):")
display(lambda_prime)
print()
# 1次導関数が0となる点(極値候補)を解く
critical_points = sp.solve(lambda_prime, x)
print("極値候補:")
display(critical_points)
print()
# 2次導関数を計算して極値の性質を確認
lambda_double_prime = sp.diff(lambda_prime, x)
print("2次導関数 λ''(x):")
display(lambda_double_prime)
print()
# 各極値候補の 2次導関数の値を調べる
for point in critical_points:
second_derivative_value = lambda_double_prime.subs(x, point)
# 極値の場所を数値評価する
point_value = point.evalf()
# 2次導関数の値も数値評価する
second_derivative_value_numeric = second_derivative_value.evalf()
if second_derivative_value > 0:
print(f"x = {point} で谷(極小値) (数値: {point_value})")
print(f"2次導関数の値: {second_derivative_value_numeric}")
elif second_derivative_value < 0:
print(f"x = {point} で山(極大値) (数値: {point_value})")
print(f"2次導関数の値: {second_derivative_value_numeric}")
else:
print(f"x = {point} で特異点か平坦な極値 (数値: {point_value})")
print(f"2次導関数の値: {second_derivative_value_numeric}")
以上のように求まりました。
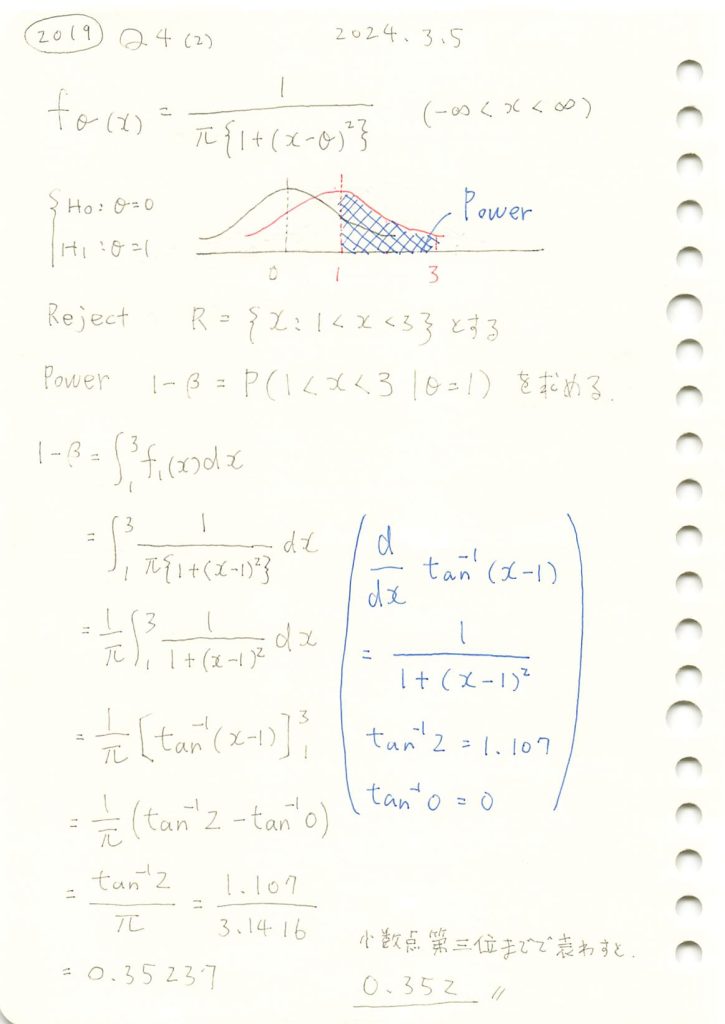
2019 Q4(2)
コーシー分布の検出力を計算しました。
コード
数式を使って検出力1-βを求めます。
# 2019 Q4(2) 2024.9.24
import numpy as np
from scipy.integrate import quad
# コーシー分布の確率密度関数 (theta = 1)
def cauchy_pdf_theta_1(x):
return 1 / (np.pi * (1 + (x - 1)**2))
# 積分範囲(棄却域R = (1, 3))
lower_bound = 1
upper_bound = 3
# 積分を実行
power, error = quad(cauchy_pdf_theta_1, lower_bound, upper_bound)
# 結果を表示(小数第3位まで表示)
print(f"検出力 (1 - β): {power:.3f}")検出力 (1 - β): 0.352手計算と一致しました。
次に、数値シミュレーションで計算をしてみます。なお、コーシー分布は裾が重いため-8 ~8の範囲になるようにフィルターを掛けることにします。
# 2019 Q4(2) 2024.9.24
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import cauchy
# シミュレーションのパラメータ
np.random.seed(43)
num_trials = 100000
# 棄却域 R = (1, 3)
lower_bound = 1
upper_bound = 3
# コーシー分布 (θ = 1) からのサンプルを生成
samples = cauchy.rvs(loc=1, scale=1, size=num_trials)
# -8 から 8 の範囲にサンプルを制限して外れ値を除外
filtered_samples = samples[(samples > -8) & (samples < 8)]
# 棄却域に入っているかどうかを判定
reject = (samples > lower_bound) & (samples < upper_bound)
# 棄却域に入った割合が検出力 (1 - β)
power_simulated = np.mean(reject)
# 結果を表示
print(f"シミュレーションによる検出力 (1 - β): {power_simulated:.3f}")
# ヒストグラムのプロット(フィルタリングしたサンプルを使う)
plt.figure(figsize=(10, 6))
plt.hist(filtered_samples, bins=100, density=True, alpha=0.5, color='blue', label='シミュレーション結果(フィルタリング済み)')
# 理論的なコーシー分布の確率密度関数 (theta = 1) をプロット
x = np.linspace(-8, 8, 1000)
pdf_theta_1 = cauchy.pdf(x, loc=1) # 対立仮説の理論曲線 (θ = 1)
plt.plot(x, pdf_theta_1, 'r-', lw=2, label='理論的コーシー分布 (θ = 1)')
# 理論的なコーシー分布の確率密度関数 (theta = 0) をプロット
pdf_theta_0 = cauchy.pdf(x, loc=0) # 帰無仮説の理論曲線 (θ = 0)
plt.plot(x, pdf_theta_0, 'g--', lw=2, label='理論的コーシー分布 (θ = 0)')
# 棄却域を塗りつぶす
plt.axvspan(lower_bound, upper_bound, color='red', alpha=0.3, label='棄却域 (1 < x < 3)')
# グラフの設定
plt.xlim(-8, 8)
plt.xlabel('x')
plt.ylabel('密度')
plt.title(f'コーシー分布のシミュレーションと棄却域\nシミュレーションによる検出力 (1 - β) = {power_simulated:.3f}')
plt.legend()
plt.grid(True)
# グラフを表示
plt.show()シミュレーションによる検出力 (1 - β): 0.355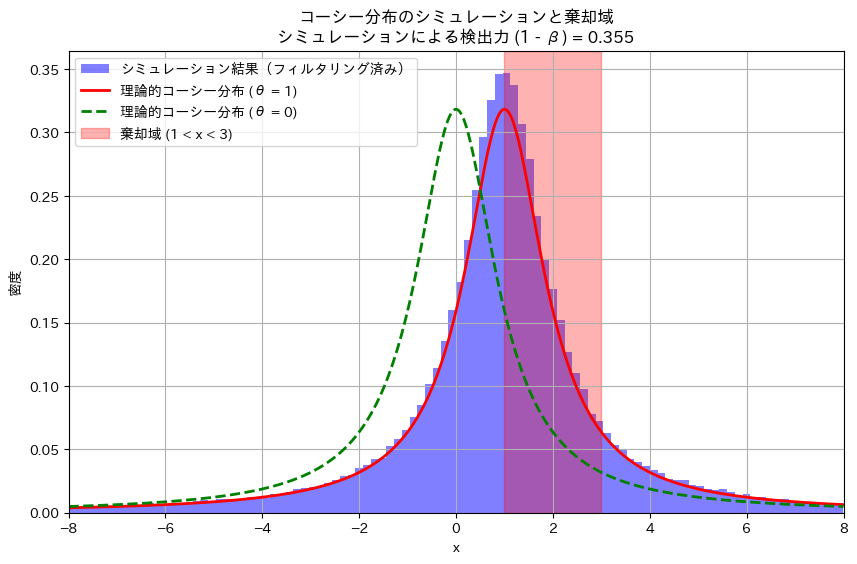
シミュレーション結果も手計算とほぼ一致しました。
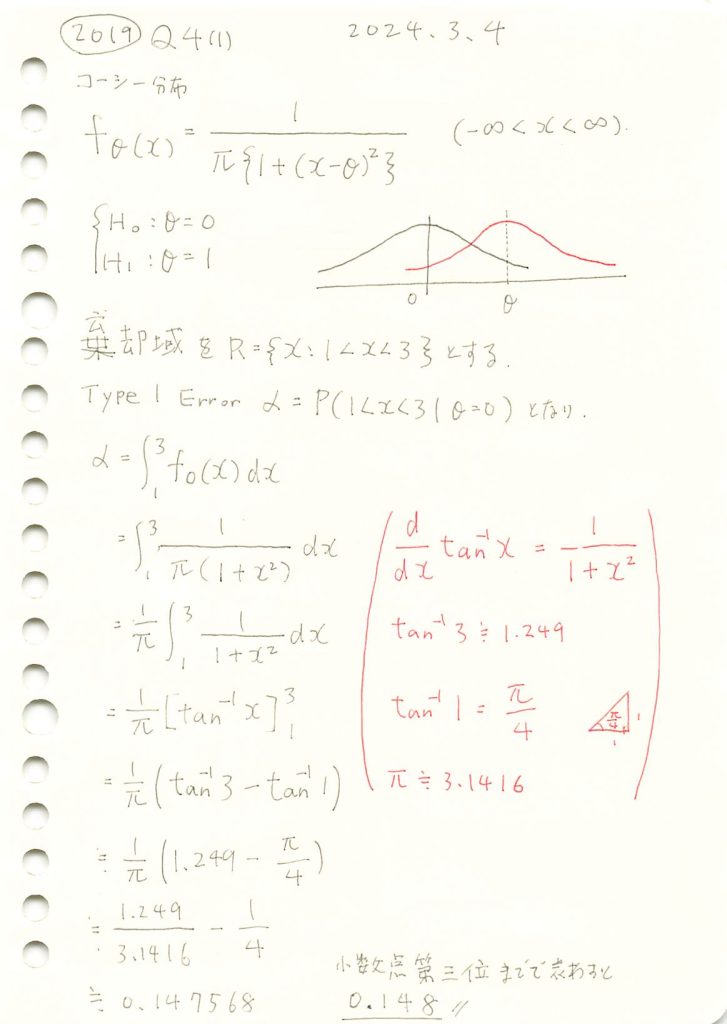
2019 Q4(1)
コーシー分布の検定での第一種過誤確率を求めました。
コード
数式を使って第一種の過誤確率αを求めます。
# 2019 Q4(1) 2024.9.23
import numpy as np
from scipy.integrate import quad
# コーシー分布の確率密度関数 (theta = 0)
def cauchy_pdf(x):
return 1 / (np.pi * (1 + x**2))
# 積分範囲(棄却域R = (1, 3))
lower_bound = 1
upper_bound = 3
# 積分を実行
alpha, error = quad(cauchy_pdf, lower_bound, upper_bound)
# 結果を表示(小数第3位まで表示)
print(f"第一種の過誤確率 α: {alpha:.3f}")第一種の過誤確率 α: 0.148手計算と一致しました。
次に、数値シミュレーションで計算をしてみます。なお、コーシー分布は裾が重いため-8 ~8の範囲になるようにフィルターを掛けることにします。
# 2019 Q4(1) 2024.9.23
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import cauchy
# シミュレーションのパラメータ
np.random.seed(43)
num_trials = 100000
# 棄却域 R = (1, 3)
lower_bound = 1
upper_bound = 3
# コーシー分布 (θ = 0) からのサンプルを生成
samples = np.random.standard_cauchy(size=num_trials)
# -8 から 8 の範囲にサンプルを制限して外れ値を除外
filtered_samples = samples[(samples > -8) & (samples < 8)]
# 棄却域に入っているかどうかを判定
reject = (samples > lower_bound) & (samples < upper_bound)
# 棄却域に入った割合が第一種の過誤確率 α
alpha_simulated = np.mean(reject)
# 結果を表示
print(f"シミュレーションによる第一種の過誤確率 α: {alpha_simulated:.3f}")
# ヒストグラムのプロット(フィルタリングしたサンプルを使う)
plt.figure(figsize=(10, 6))
plt.hist(filtered_samples, bins=100, density=True, alpha=0.5, color='blue', label='シミュレーション結果(フィルタリング済み)')
# 理論的なコーシー分布の確率密度関数 (theta = 0) をプロット
x = np.linspace(-8, 8, 1000) # 横のレンジを -8 から 8 に設定
pdf = cauchy.pdf(x)
plt.plot(x, pdf, 'r-', lw=2, label='理論的コーシー分布の確率密度関数')
# 棄却域を塗りつぶす
plt.axvspan(lower_bound, upper_bound, color='red', alpha=0.3, label='棄却域 (1 < x < 3)')
# グラフの設定
plt.xlim(-8, 8) # 横のレンジを -8 から 8 に設定
plt.xlabel('x')
plt.ylabel('密度')
plt.title(f'コーシー分布のシミュレーションと棄却域\nシミュレーションによる α = {alpha_simulated:.3f}')
plt.legend()
plt.grid(True)
# グラフを表示
plt.show()シミュレーションによる第一種の過誤確率 α: 0.148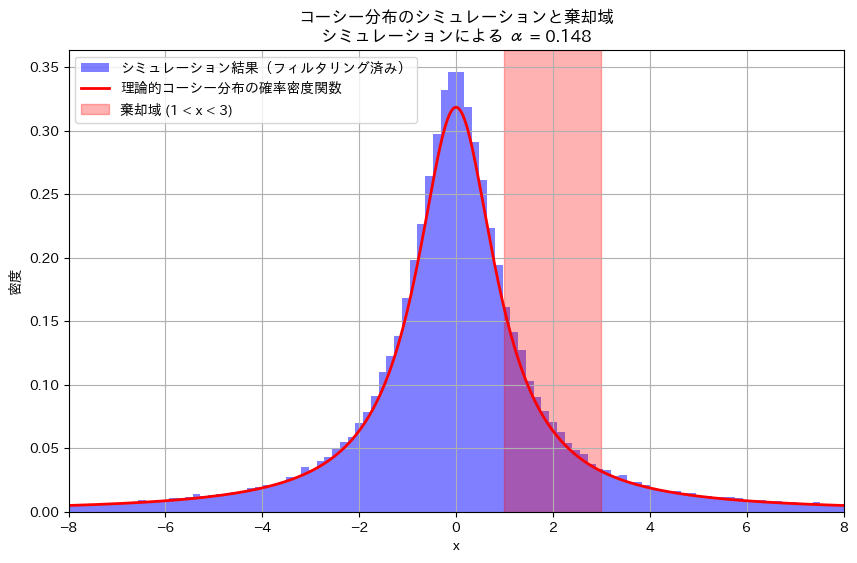
シミュレーション結果も手計算と一致しました。