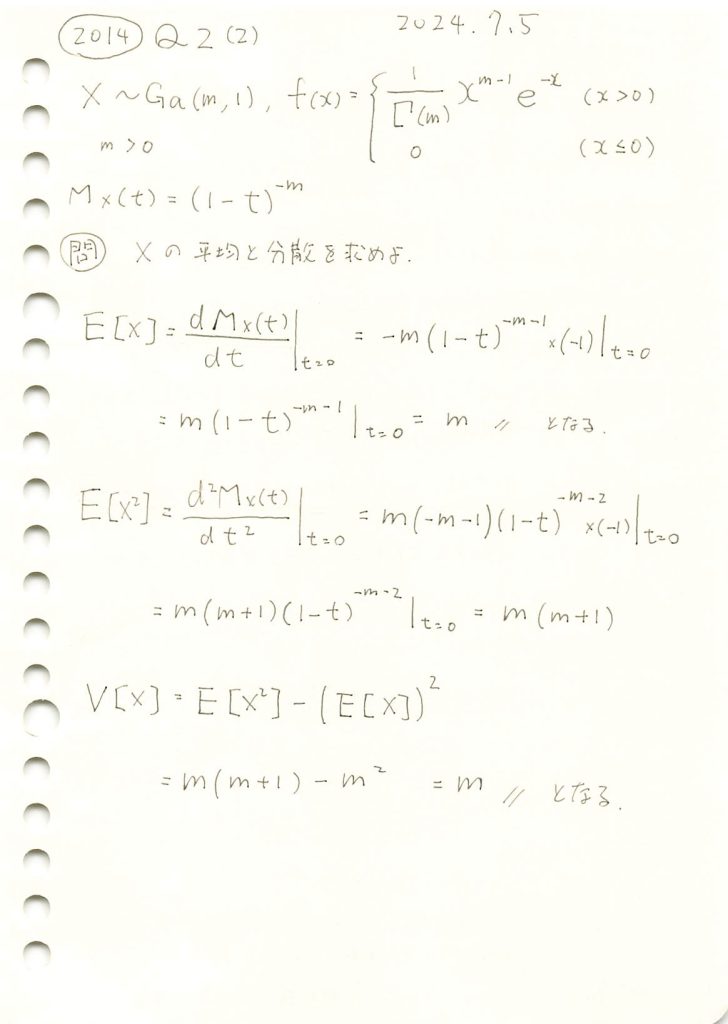ホーム » 分布
「分布」カテゴリーアーカイブ
二項分布と超幾何分布
二項分布
- 抽出方法: 復元抽出
- 試行の独立性: 各試行は独立
- 確率: 各試行で成功確率は一定
超幾何分布
- 抽出方法: 非復元抽出
- 試行の独立性: 各試行は独立していない
- 確率: 各試行で成功確率が変化
グラフの比較
今回の実験では、二項分布と超幾何分布の違いを視覚的に比較します。二項分布は、復元抽出を行う場合に適用され、各試行が独立しており、成功確率が一定です。一方、超幾何分布は、非復元抽出を行う場合に適用され、試行ごとに成功確率が変化します。実験では、母集団のサイズ、成功対象の数、抽出回数を変え、それぞれのグラフを描画します。特に、サンプルサイズが大きい場合や母集団が小さい場合など、分布の形状に顕著な違いが現れる条件に注目して比較を行います。これにより、抽出方法による分布の違いを視覚的に確認し、二項分布と超幾何分布の特性を理解します。
復元抽出と非復元抽出の比較(広範囲のパラメータ設定)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, hypergeom
# グラフを描画する関数
def plot_comparison(M, N_A, n, ax):
# 非復元抽出(超幾何分布)
rv_hypergeom = hypergeom(M, N_A, n)
x_values = np.arange(0, n+1)
pmf_hypergeom = rv_hypergeom.pmf(x_values)
# 復元抽出(二項分布)
p = N_A / M # 豆Aを引く確率
rv_binom = binom(n, p)
pmf_binom = rv_binom.pmf(x_values)
# グラフ描画
ax.plot(x_values, pmf_hypergeom, 'bo-', label='非復元抽出 (超幾何分布)', markersize=5)
ax.plot(x_values, pmf_binom, 'ro-', label='復元抽出 (二項分布)', markersize=5)
condition_text = f'M = {M}, N_A = {N_A}, n = {n}'
ax.text(0.05, 0.95, condition_text, transform=ax.transAxes,
fontsize=12, verticalalignment='top')
ax.set_xlabel('豆Aの数')
ax.set_ylabel('確率')
ax.grid(True)
ax.legend()
# パラメータ比を一定に保ったグラフを作成
M_values = [50, 150, 250, 350, 450]
N_A_values = [15, 45, 75, 105, 135] # M の 30%
n_values = [7, 22, 37, 52, 67] # M の 15%
# サブプロットを作成(縦に並べる)
fig, axs = plt.subplots(5, 1, figsize=(10, 30))
# 異なるパラメータ設定でグラフを描画
for i in range(5):
plot_comparison(M=M_values[i], N_A=N_A_values[i], n=n_values[i], ax=axs[i])
# レイアウトの自動調整
plt.tight_layout()
# 余白の手動調整
plt.subplots_adjust(right=0.95)
plt.show()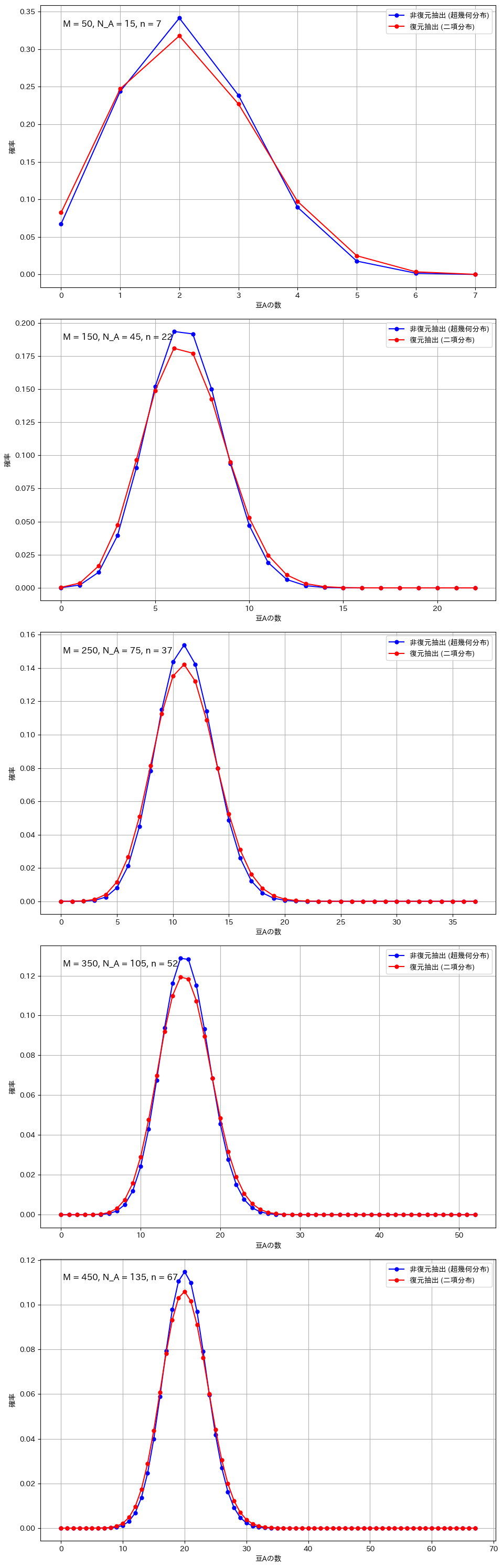
復元抽出と非復元抽出の比較(顕著な違いが現れる条件)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, hypergeom
# グラフを描画する関数
def plot_comparison(M, N_A, n, ax):
# 非復元抽出(超幾何分布)
rv_hypergeom = hypergeom(M, N_A, n)
x_values = np.arange(0, n+1)
pmf_hypergeom = rv_hypergeom.pmf(x_values)
# 復元抽出(二項分布)
p = N_A / M # 豆Aを引く確率
rv_binom = binom(n, p)
pmf_binom = rv_binom.pmf(x_values)
# グラフ描画
ax.plot(x_values, pmf_hypergeom, 'bo-', label='非復元抽出 (超幾何分布)', markersize=5)
ax.plot(x_values, pmf_binom, 'ro-', label='復元抽出 (二項分布)', markersize=5)
condition_text = f'M = {M}, N_A = {N_A}, n = {n}'
ax.text(0.05, 0.95, condition_text, transform=ax.transAxes,
fontsize=12, verticalalignment='top')
ax.set_xlabel('豆Aの数')
ax.set_ylabel('確率')
ax.grid(True)
ax.legend()
# サブプロットを作成(縦に並べる)
fig, axs = plt.subplots(3, 1, figsize=(10, 18)) # 高さを調整
# 条件1: サンプルサイズが大きい場合
plot_comparison(M=100, N_A=30, n=80, ax=axs[0])
# 条件2: 全体のサイズが小さい場合
plot_comparison(M=20, N_A=6, n=15, ax=axs[1])
# 条件3: 極端な割合の場合
plot_comparison(M=100, N_A=90, n=30, ax=axs[2])
# レイアウトの自動調整
plt.tight_layout()
# 余白の手動調整
plt.subplots_adjust(right=0.95)
plt.show()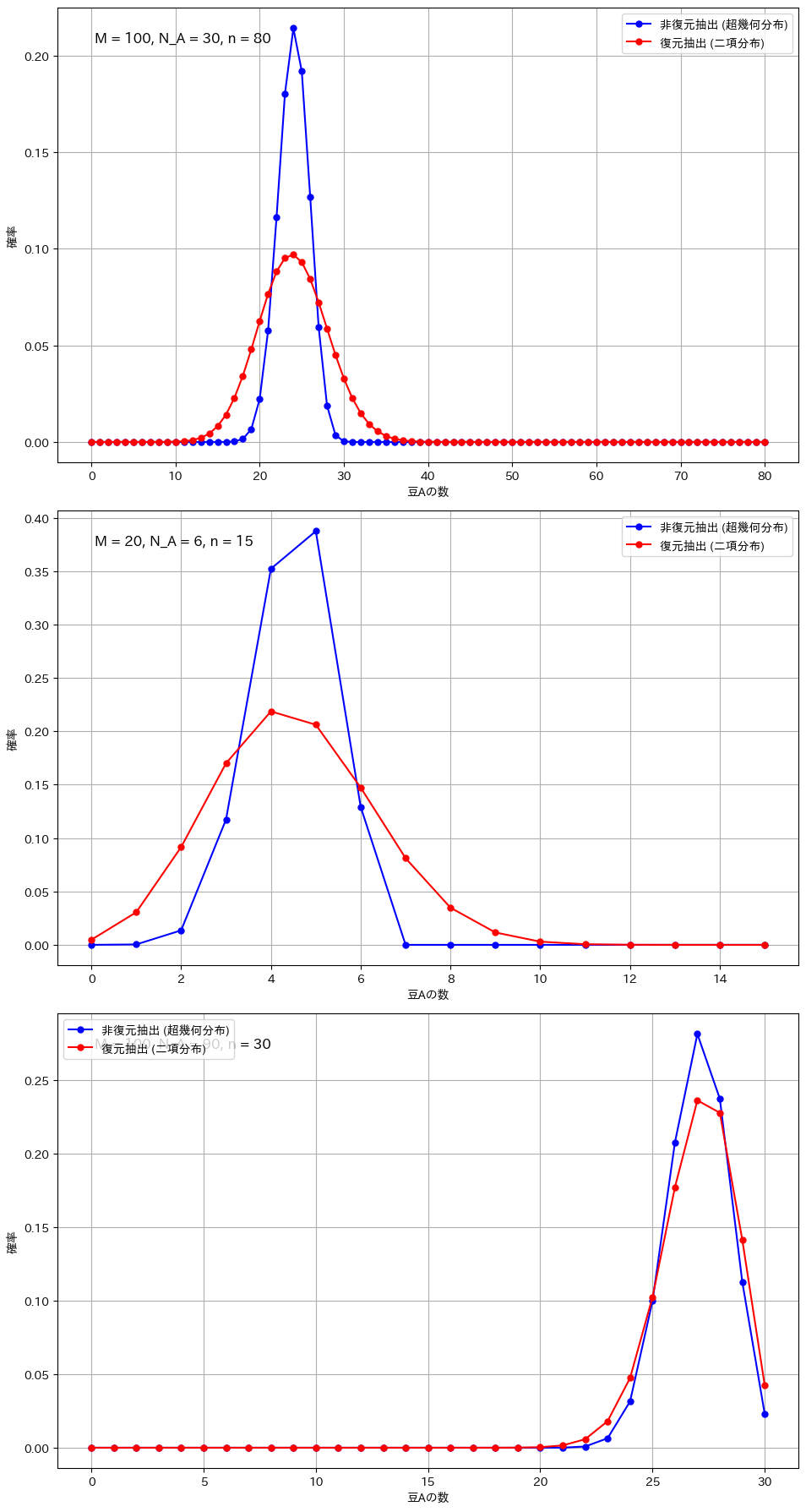
考察
二項分布と超幾何分布の違いが顕著になるのは、サンプルサイズが全体に対して大きい場合や、母集団が小さい場合です。例えば、全体の豆の数が100個で80個を抽出する場合や、母集団が20個でそのうち15個を抽出する場合、非復元抽出では次の試行に与える影響が大きくなり、復元抽出との差が明確に現れます。また、成功確率が極端に高いか低い場合も、非復元抽出の影響で分布が変わりやすくなります。一方、サンプルサイズが小さい場合や母集団が非常に大きい場合には、各抽出の影響が少なく、二項分布と超幾何分布の違いは目立たなくなります。
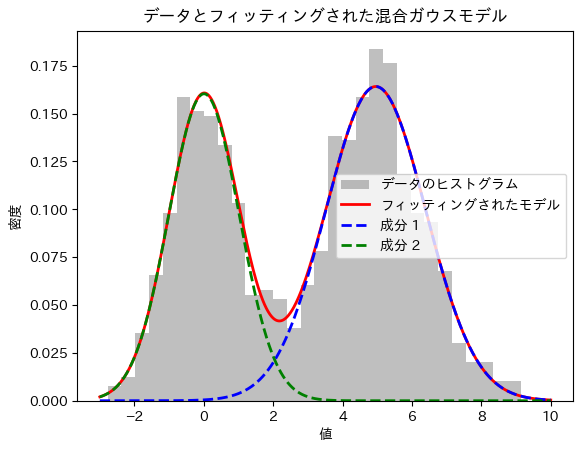
混合ガウスモデルによる観測データの分布特性推定
概要:
本実験では、観測データが複数の異なる分布の混合によって生成されている可能性を考慮し、その分布特性を推定する手法を検証する。具体的には、2つの正規分布を混合したデータを生成し、EMアルゴリズムを用いてその混合ガウスモデルをフィッティングする。実験の結果、生成されたデータの背後にある各分布の平均、標準偏差、および混合割合を高精度に推定できることを確認した。本手法は、複雑な観測データに対する分布特性の解析やデータの要因分解に有効である。
2つの成分
import numpy as np
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
# 1. データ生成: 混合正規分布から乱数を生成
np.random.seed(0)
n_samples = 1000
# 2つの正規分布のパラメータ設定
mean1, std1 = 0, 1 # 正規分布1
mean2, std2 = 5, 1.5 # 正規分布2
weight1, weight2 = 0.4, 0.6 # 混合割合
# 2つの分布からデータ生成
data1 = np.random.normal(mean1, std1, int(weight1 * n_samples))
data2 = np.random.normal(mean2, std2, int(weight2 * n_samples))
# 混合データの作成
data = np.hstack([data1, data2])
np.random.shuffle(data)
# 2. 混合モデルの構築とフィッティング (EMアルゴリズムを使用)
gmm = GaussianMixture(n_components=2, random_state=0)
gmm.fit(data.reshape(-1, 1))
# 推定されたパラメータ
means = gmm.means_.flatten()
std_devs = np.sqrt(gmm.covariances_).flatten()
weights = gmm.weights_
print("推定された平均:", means)
print("推定された標準偏差:", std_devs)
print("推定された混合割合:", weights)
# 3. 結果のプロット
x = np.linspace(-3, 10, 1000)
pdf1 = weights[0] * (1 / (std_devs[0] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[0])**2 / (2 * std_devs[0]**2)))
pdf2 = weights[1] * (1 / (std_devs[1] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[1])**2 / (2 * std_devs[1]**2)))
plt.hist(data, bins=30, density=True, alpha=0.5, color='gray', label='データのヒストグラム')
plt.plot(x, pdf1 + pdf2, 'r-', lw=2, label='フィッティングされたモデル')
plt.plot(x, pdf1, 'b--', lw=2, label='成分 1')
plt.plot(x, pdf2, 'g--', lw=2, label='成分 2')
plt.title('データとフィッティングされた混合ガウスモデル')
plt.xlabel('値')
plt.ylabel('密度')
plt.legend()
plt.show()
3つの成分
import numpy as np
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
# 1. データ生成: 混合正規分布から乱数を生成
np.random.seed(0)
n_samples = 1000
# 3つの正規分布のパラメータ設定
mean1, std1 = 0, 1 # 正規分布1
mean2, std2 = 5, 1.5 # 正規分布2
mean3, std3 = 10, 2 # 正規分布3
weight1, weight2, weight3 = 0.3, 0.4, 0.3 # 混合割合
# 3つの分布からデータ生成
data1 = np.random.normal(mean1, std1, int(weight1 * n_samples))
data2 = np.random.normal(mean2, std2, int(weight2 * n_samples))
data3 = np.random.normal(mean3, std3, int(weight3 * n_samples))
# 混合データの作成
data = np.hstack([data1, data2, data3])
np.random.shuffle(data)
# 2. 混合モデルの構築とフィッティング (EMアルゴリズムを使用)
gmm = GaussianMixture(n_components=3, random_state=0)
gmm.fit(data.reshape(-1, 1))
# 推定されたパラメータ
means = gmm.means_.flatten()
std_devs = np.sqrt(gmm.covariances_).flatten()
weights = gmm.weights_
print("推定された平均:", means)
print("推定された標準偏差:", std_devs)
print("推定された混合割合:", weights)
# 3. 結果のプロット
x = np.linspace(-5, 15, 1000)
pdf1 = weights[0] * (1 / (std_devs[0] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[0])**2 / (2 * std_devs[0]**2)))
pdf2 = weights[1] * (1 / (std_devs[1] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[1])**2 / (2 * std_devs[1]**2)))
pdf3 = weights[2] * (1 / (std_devs[2] * np.sqrt(2 * np.pi)) * np.exp(-(x - means[2])**2 / (2 * std_devs[2]**2)))
plt.hist(data, bins=30, density=True, alpha=0.5, color='gray', label='データのヒストグラム')
plt.plot(x, pdf1 + pdf2 + pdf3, 'r-', lw=2, label='フィッティングされたモデル')
plt.plot(x, pdf1, 'b--', lw=2, label='成分 1')
plt.plot(x, pdf2, 'g--', lw=2, label='成分 2')
plt.plot(x, pdf3, 'y--', lw=2, label='成分 3')
plt.title('データとフィッティングされた混合ガウスモデル')
plt.xlabel('値')
plt.ylabel('密度')
plt.legend()
plt.show()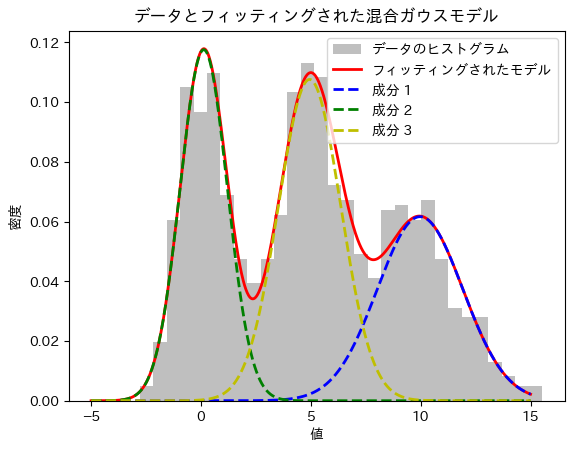
2014 Q5(4)
テレビ番組の視聴満足回数の調査で満足と答えた回数のそれぞれ人数の適合度検定を実施し適合を判断する手順を述べました。

コード
多項確率![]() が、
が、![]() に忠実に基づく場合と、各番組または各回答者の満足度が異なるモデルにおいて、カイ二乗統計量、尤度比統計量、およびp-値を計算し、モデルの適合性を比較します。
に忠実に基づく場合と、各番組または各回答者の満足度が異なるモデルにおいて、カイ二乗統計量、尤度比統計量、およびp-値を計算し、モデルの適合性を比較します。
import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
# シミュレーションの設定
n = 100 # 回答者数
p_true = 0.6 # 真の成功確率(忠実なモデル)
categories = np.arange(5) # カテゴリ (0~4)
n_simulations = 1000 # シミュレーション回数
# 忠実なモデルの確率 q_j
qj_true = [np.math.comb(4, j) * (p_true ** j) * ((1 - p_true) ** (4 - j)) for j in categories]
# 統計量を記録するリスト
chi_squared_true = []
likelihood_ratio_true = []
chi_squared_noisy_program = []
likelihood_ratio_noisy_program = []
chi_squared_noisy_responder = []
likelihood_ratio_noisy_responder = []
# 二項分布に従わない (qj_noisy_program): q_j をランダムに変更してズラす
qj_noisy_program = np.array(qj_true) + np.random.uniform(-0.1, 0.1, size=len(qj_true))
qj_noisy_program = np.clip(qj_noisy_program, 0, None) # 確率が0未満にならないようにする
qj_noisy_program = qj_noisy_program / np.sum(qj_noisy_program) # 確率なので正規化
# 各回答者の満足度が異なる場合(qj_noisy_responder)をランダム設定
p_responders = np.random.uniform(0.35, 0.85, size=n)
qj_noisy_responder = np.zeros(len(categories))
for p in p_responders:
qj_responder = [np.math.comb(4, j) * (p ** j) * ((1 - p) ** (4 - j)) for j in categories]
qj_noisy_responder += qj_responder
qj_noisy_responder /= np.sum(qj_noisy_responder)
# シミュレーション開始
for _ in range(n_simulations):
# 忠実なモデル(均一)
obs_true = np.random.multinomial(n, qj_true)
exp_true = n * np.array(qj_true)
chi2_stat_true = np.sum((obs_true - exp_true) ** 2 / exp_true) # カイ二乗統計量
likelihood_stat_true = 2 * np.sum(obs_true * np.log(obs_true / exp_true, where=(obs_true > 0))) # 尤度比統計量
chi_squared_true.append(chi2_stat_true)
likelihood_ratio_true.append(likelihood_stat_true)
# 各番組の満足度が異なる場合
obs_noisy_program = np.random.multinomial(n, qj_noisy_program)
exp_noisy_program = n * np.array(qj_true)
chi2_stat_noisy_program = np.sum((obs_noisy_program - exp_noisy_program) ** 2 / exp_noisy_program) # カイ二乗統計量
likelihood_stat_noisy_program = 2 * np.sum(obs_noisy_program * np.log(obs_noisy_program / exp_noisy_program, where=(obs_noisy_program > 0))) # 尤度比統計量
chi_squared_noisy_program.append(chi2_stat_noisy_program)
likelihood_ratio_noisy_program.append(likelihood_stat_noisy_program)
# 各回答者の満足度が異なる場合
obs_noisy_responder = np.random.multinomial(n, qj_noisy_responder)
exp_noisy_responder = n * np.array(qj_true)
chi2_stat_noisy_responder = np.sum((obs_noisy_responder - exp_noisy_responder) ** 2 / exp_noisy_responder) # カイ二乗統計量
likelihood_stat_noisy_responder = 2 * np.sum(obs_noisy_responder * np.log(obs_noisy_responder / exp_noisy_responder, where=(obs_noisy_responder > 0))) # 尤度比統計量
chi_squared_noisy_responder.append(chi2_stat_noisy_responder)
likelihood_ratio_noisy_responder.append(likelihood_stat_noisy_responder)
# 平均値を計算
mean_chi2_true = np.mean(chi_squared_true)
mean_likelihood_true = np.mean(likelihood_ratio_true)
mean_chi2_noisy_program = np.mean(chi_squared_noisy_program)
mean_likelihood_noisy_program = np.mean(likelihood_ratio_noisy_program)
mean_chi2_noisy_responder = np.mean(chi_squared_noisy_responder)
mean_likelihood_noisy_responder = np.mean(likelihood_ratio_noisy_responder)
# 各統計量に対応するp値を計算
p_value_chi2_true = 1 - chi2.cdf(mean_chi2_true, df=3)
p_value_likelihood_true = 1 - chi2.cdf(mean_likelihood_true, df=3)
p_value_chi2_noisy_program = 1 - chi2.cdf(mean_chi2_noisy_program, df=3)
p_value_likelihood_noisy_program = 1 - chi2.cdf(mean_likelihood_noisy_program, df=3)
p_value_chi2_noisy_responder = 1 - chi2.cdf(mean_chi2_noisy_responder, df=3)
p_value_likelihood_noisy_responder = 1 - chi2.cdf(mean_likelihood_noisy_responder, df=3)
# 結果の出力
print(f"忠実なモデル(均一)の平均カイ二乗統計量: {mean_chi2_true:.4f}, 平均p値: {p_value_chi2_true:.4f}")
print(f"忠実なモデル(均一)の平均尤度比統計量: {mean_likelihood_true:.4f}, 平均p値: {p_value_likelihood_true:.4f}")
print(f"各番組の満足度が異なる場合の平均カイ二乗統計量: {mean_chi2_noisy_program:.4f}, 平均p値: {p_value_chi2_noisy_program:.4f}")
print(f"各番組の満足度が異なる場合の平均尤度比統計量: {mean_likelihood_noisy_program:.4f}, 平均p値: {p_value_likelihood_noisy_program:.4f}")
print(f"各回答者の満足度が異なる場合の平均カイ二乗統計量: {mean_chi2_noisy_responder:.4f}, 平均p値: {p_value_chi2_noisy_responder:.4f}")
print(f"各回答者の満足度が異なる場合の平均尤度比統計量: {mean_likelihood_noisy_responder:.4f}, 平均p値: {p_value_likelihood_noisy_responder:.4f}")
# カイ二乗分布のPDFを計算
x = np.linspace(0, 20, 500) # x軸の範囲
pdf = chi2.pdf(x, df=3) # 自由度3のPDF
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(x, pdf, label="自由度3のカイ二乗分布", linewidth=2)
plt.axvline(mean_chi2_true, color="blue", linestyle="--", label=f"忠実モデルのカイ二乗: {mean_chi2_true:.2f}")
plt.axvline(mean_likelihood_true, color="cyan", linestyle="--", label=f"忠実モデルの尤度比: {mean_likelihood_true:.2f}")
plt.axvline(mean_chi2_noisy_program, color="green", linestyle="--", label=f"番組ごとに異なるカイ二乗: {mean_chi2_noisy_program:.2f}")
plt.axvline(mean_likelihood_noisy_program, color="lime", linestyle="--", label=f"番組ごとに異なる尤度比: {mean_likelihood_noisy_program:.2f}")
plt.axvline(mean_chi2_noisy_responder, color="red", linestyle="--", label=f"回答者ごとに異なるカイ二乗: {mean_chi2_noisy_responder:.2f}")
plt.axvline(mean_likelihood_noisy_responder, color="magenta", linestyle="--", label=f"回答者ごとに異なる尤度比: {mean_likelihood_noisy_responder:.2f}")
plt.xlabel("$X^2$ 値", fontsize=12)
plt.ylabel
plt.ylabel("確率密度", fontsize=12)
plt.title("自由度3のカイ二乗分布と統計量", fontsize=14)
plt.legend(fontsize=12) # ここで凡例を表示
plt.grid(alpha=0.5)
plt.show()忠実なモデル(均一)の平均カイ二乗統計量: 4.1751, 平均p値: 0.2432
忠実なモデル(均一)の平均尤度比統計量: 4.3247, 平均p値: 0.2285
各番組の満足度が異なる場合の平均カイ二乗統計量: 13.2002, 平均p値: 0.0042
各番組の満足度が異なる場合の平均尤度比統計量: 16.4412, 平均p値: 0.0009
各回答者の満足度が異なる場合の平均カイ二乗統計量: 10.3066, 平均p値: 0.0161
各回答者の満足度が異なる場合の平均尤度比統計量: 8.5302, 平均p値: 0.0362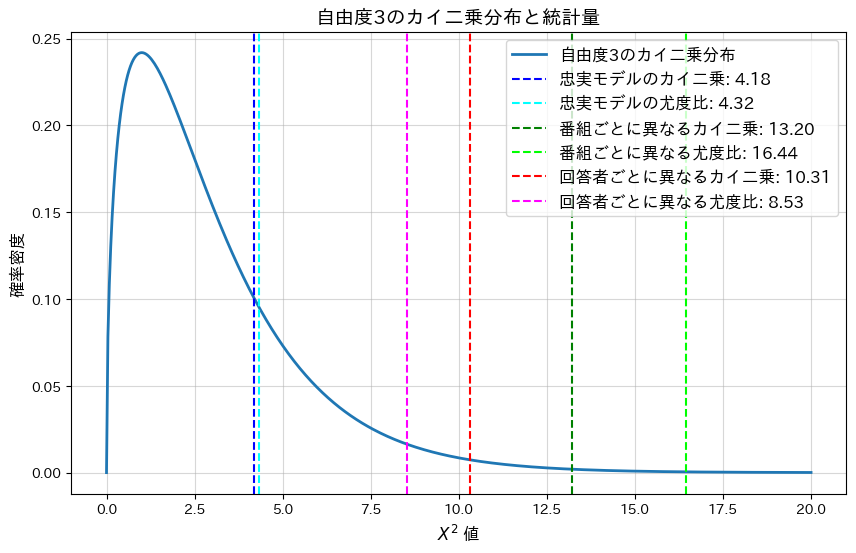
忠実なモデルの平均p-値は大きく、モデルによく適合していることが分かります。一方、各番組または各回答者の満足度が異なるモデルではp-値が0.05以下となり、モデルがデータに適合していないことが分かります。
2014 Q5(3)
テレビ番組の視聴満足回数の調査で満足と答えた回数のそれぞれ人数の適合度検定のための尤度比検定量と自由度を求めました。

コード
多項確率![]() が、
が、![]() に忠実に基づく場合と、ランダムにノイズを加えた(ズレた)場合についてシミュレーションを行い、尤度比統計量とp-値を計算して比較します。
に忠実に基づく場合と、ランダムにノイズを加えた(ズレた)場合についてシミュレーションを行い、尤度比統計量とp-値を計算して比較します。
# 2014 Q5(3) 2025.1.17
import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
# シミュレーションの設定
n = 100 # 人数
p_true = 0.6 # 真の成功確率
categories = np.arange(5) # カテゴリ (0~4)
n_simulations = 1000 # シミュレーション回数
# 二項分布モデルに基づく q_j の計算 (忠実な設定)
qj_true = [np.math.comb(4, j) * (p_true ** j) * ((1 - p_true) ** (4 - j)) for j in categories]
# 二項分布に従わない (qj_noisy): q_j をランダムに変更してズラす
qj_noisy = np.array(qj_true) + np.random.uniform(-0.1, 0.1, size=len(qj_true))
qj_noisy = np.clip(qj_noisy, 0, None) # 確率が0未満にならないようにする
qj_noisy = qj_noisy / np.sum(qj_noisy) # 確率なので正規化
# 尤度比統計量を記録するリスト
likelihood_ratio_true = []
p_values_true = []
likelihood_ratio_noisy = []
p_values_noisy = []
for _ in range(n_simulations):
# 忠実なモデルの観測データ
obs_true = np.random.multinomial(n, qj_true)
exp_true = n * np.array(qj_true)
likelihood_stat_true = 2 * np.sum(obs_true * np.log(obs_true / exp_true, where=(obs_true > 0)))
p_val_true = 1 - chi2.cdf(likelihood_stat_true, df=3) # 自由度 = カテゴリ数 - 1 - 推定パラメータ数
likelihood_ratio_true.append(likelihood_stat_true)
p_values_true.append(p_val_true)
# ズレたモデルの観測データ
obs_noisy = np.random.multinomial(n, qj_noisy)
exp_noisy = n * np.array(qj_true) # 忠実な期待値を使用
likelihood_stat_noisy = 2 * np.sum(obs_noisy * np.log(obs_noisy / exp_noisy, where=(obs_noisy > 0)))
p_val_noisy = 1 - chi2.cdf(likelihood_stat_noisy, df=3)
likelihood_ratio_noisy.append(likelihood_stat_noisy)
p_values_noisy.append(p_val_noisy)
# 平均尤度比統計量を計算
mean_likelihood_true = np.mean(likelihood_ratio_true)
mean_likelihood_noisy = np.mean(likelihood_ratio_noisy)
# カイ二乗分布のPDFを計算
x = np.linspace(0, 20, 500) # x軸の範囲
pdf = chi2.pdf(x, df=3) # 自由度3のPDF
# 結果の出力
print(f"忠実なモデルの平均尤度比統計量: {mean_likelihood_true:.4f}")
print(f"忠実なモデルの平均p値: {np.mean(p_values_true):.4f}")
print(f"ズレたモデルの平均尤度比統計量: {mean_likelihood_noisy:.4f}")
print(f"ズレたモデルの平均p値: {np.mean(p_values_noisy):.4f}")
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(x, pdf, label="自由度3のカイ二乗分布", linewidth=2)
plt.axvline(mean_likelihood_true, color="blue", linestyle="--", label=f"忠実モデルの平均: {mean_likelihood_true:.2f}")
plt.axvline(mean_likelihood_noisy, color="red", linestyle="--", label=f"ズレモデルの平均: {mean_likelihood_noisy:.2f}")
plt.xlabel("$X^2$ 値", fontsize=12)
plt.ylabel("確率密度", fontsize=12)
plt.title("自由度3のカイ二乗分布と平均尤度比統計量", fontsize=14)
plt.legend(fontsize=12)
plt.grid(alpha=0.5)
plt.show()忠実なモデルの平均尤度比統計量: 3.9418
忠実なモデルの平均p値: 0.3909
ズレたモデルの平均尤度比統計量: 16.7360
ズレたモデルの平均p値: 0.0081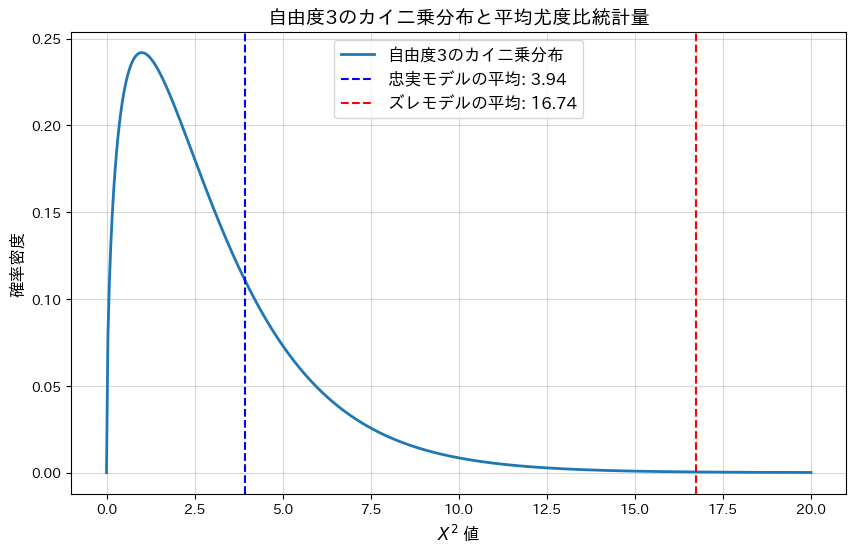
忠実なモデルの平均p-値は大きく、モデルによく適合していることが分かります。一方、ランダムにノイズを加えた(ズレた)モデルではp-値が0.05以下となり、モデルがデータに適合していないことが分かります。
2014 Q5(2)
テレビ番組の視聴満足回数の調査で満足と答えた回数のそれぞれ人数の適合度カイ二乗統計量と自由度を求めました。

コード
多項確率![]() が、
が、![]() に忠実に基づく場合と、ランダムにノイズを加えた(ズレた)場合についてシミュレーションを行い、適合度カイ二乗統計量とp-値を計算して比較します。
に忠実に基づく場合と、ランダムにノイズを加えた(ズレた)場合についてシミュレーションを行い、適合度カイ二乗統計量とp-値を計算して比較します。
# 2014 Q5(2) 2025.1.16
import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
# シミュレーションの設定
n = 100 # 人数
p_true = 0.6 # 真の成功確率
categories = np.arange(5) # カテゴリ (0~4)
n_simulations = 1000 # シミュレーション回数
# 二項分布モデルに基づく q_j の計算 (忠実な設定)
qj_true = [np.math.comb(4, j) * (p_true ** j) * ((1 - p_true) ** (4 - j)) for j in categories]
# 二項分布に従わない (qj_noisy): q_j をランダムに変更してズラす
qj_noisy = np.array(qj_true) + np.random.uniform(-0.1, 0.1, size=len(qj_true))
qj_noisy = np.clip(qj_noisy, 0, None) # 確率が0未満にならないようにする
qj_noisy = qj_noisy / np.sum(qj_noisy) # 確率なので正規化
# カイ二乗統計量と p 値を記録するリスト
chi_squared_true = []
p_values_true = []
chi_squared_noisy = []
p_values_noisy = []
for _ in range(n_simulations):
# 忠実なモデルの観測データ
obs_true = np.random.multinomial(n, qj_true)
exp_true = n * np.array(qj_true)
chi2_stat_true = np.sum((obs_true - exp_true) ** 2 / exp_true)
p_val_true = 1 - chi2.cdf(chi2_stat_true, df=3) # 自由度 = カテゴリ数 - 1 - 推定パラメータ数
chi_squared_true.append(chi2_stat_true)
p_values_true.append(p_val_true)
# ズレたモデルの観測データ
obs_noisy = np.random.multinomial(n, qj_noisy)
exp_noisy = n * np.array(qj_true) # 忠実な期待値を使用
chi2_stat_noisy = np.sum((obs_noisy - exp_noisy) ** 2 / exp_noisy)
p_val_noisy = 1 - chi2.cdf(chi2_stat_noisy, df=3)
chi_squared_noisy.append(chi2_stat_noisy)
p_values_noisy.append(p_val_noisy)
# 平均カイ二乗統計量を計算
mean_chi2_true = np.mean(chi_squared_true)
mean_chi2_noisy = np.mean(chi_squared_noisy)
# カイ二乗分布のPDFを計算
x = np.linspace(0, 20, 500) # x軸の範囲
pdf = chi2.pdf(x, df=3) # 自由度3のPDF
# 結果の出力
print(f"忠実なモデルの平均カイ二乗統計量: {mean_chi2_true:.4f}")
print(f"忠実なモデルの平均p値: {np.mean(p_values_true):.4f}")
print(f"ズレたモデルの平均カイ二乗統計量: {mean_chi2_noisy:.4f}")
print(f"ズレたモデルの平均p値: {np.mean(p_values_noisy):.4f}")
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(x, pdf, label="自由度3のカイ二乗分布", linewidth=2)
plt.axvline(mean_chi2_true, color="blue", linestyle="--", label=f"忠実モデルの平均: {mean_chi2_true:.2f}")
plt.axvline(mean_chi2_noisy, color="red", linestyle="--", label=f"ズレモデルの平均: {mean_chi2_noisy:.2f}")
plt.xlabel("$X^2$ 値", fontsize=12)
plt.ylabel("確率密度", fontsize=12)
plt.title("自由度3のカイ二乗分布と平均カイ二乗統計量", fontsize=14)
plt.legend(fontsize=12)
plt.grid(alpha=0.5)
plt.show()忠実なモデルの平均カイ二乗統計量: 3.8112
忠実なモデルの平均p値: 0.4026
ズレたモデルの平均カイ二乗統計量: 13.4317
ズレたモデルの平均p値: 0.0236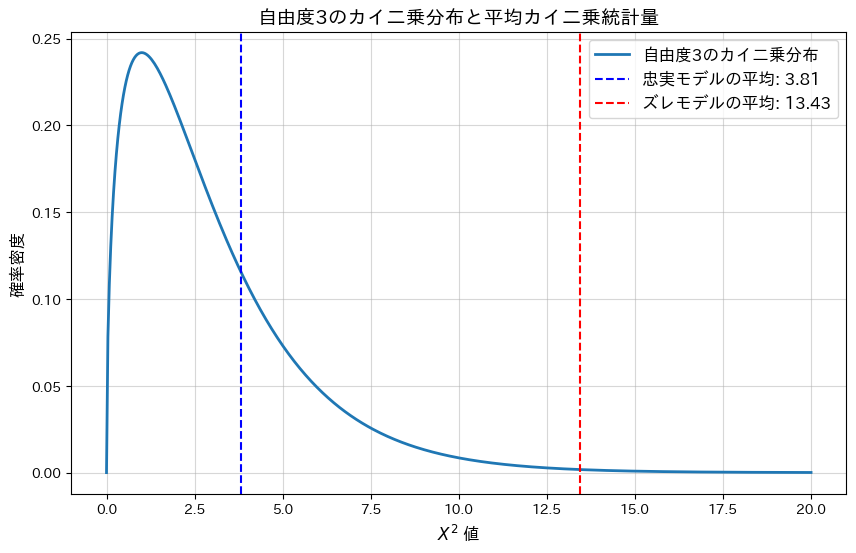
忠実なモデルの平均p-値は大きく、モデルによく適合していることが分かります。一方、ランダムにノイズを加えた(ズレた)モデルではp-値が0.05以下となり、モデルがデータに適合していないことが分かります。
2014 Q5(1)
テレビ番組の視聴満足回数の調査で満足と答えた回数のそれぞれ人数との組みが多項分布に従うのを利用し多項確率を構成する二項分布の確率pの最尤推定量を求めました。
コード
真の確率pに基づいてシミュレーションを行い、最尤推定値![]() を計算し、真の確率pと比較します。
を計算し、真の確率pと比較します。
# 2014 Q5(1) 2025.1.15
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
n_simulations = 10000 # シミュレーション回数
n = 100 # 調査対象の人数
p_true = 0.6 # 真の満足確率
# nj のシミュレーション (j = 0, 1, 2, 3, 4)
data = np.random.binomial(4, p_true, size=n_simulations * n).reshape(n_simulations, n)
# 各シミュレーションでの最尤推定値を計算
p_estimates = np.sum(data, axis=1) / (4 * n)
# 平均値(推定されたp^の期待値)を計算
mean_p_estimate = np.mean(p_estimates)
# 推定されたp^の平均値と真の値を出力
print(f"推定された最尤推定値の平均: {mean_p_estimate:.4f}")
print(f"真の値: {p_true:.4f}")
# グラフの描画
plt.hist(p_estimates, bins=30, density=True, alpha=0.75, label="推定された $\\hat{p}$")
plt.axvline(p_true, color='red', linestyle='dashed', label=f"真の値 $p = {p_true}$")
plt.xlabel("推定された $\\hat{p}$")
plt.ylabel("密度")
plt.title("最尤推定値 $\\hat{p}$ の分布")
plt.legend()
plt.grid(alpha=0.5)
plt.show()推定された最尤推定値の平均: 0.5997
真の値: 0.6000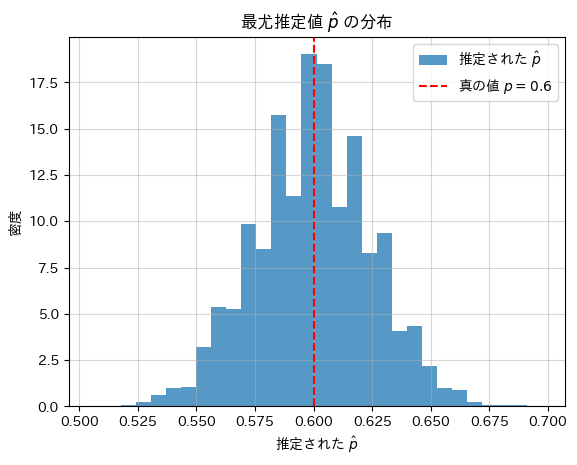
シミュレーションの結果、最尤推定値![]() は、真の確率pに近い値を示しました。
は、真の確率pに近い値を示しました。
2014 Q2(5)
n個の一様分布の順序統計量の期待値を求めました。
コード
サンプルサイズn=5として、一様分布の順序統計量![]() をシミュレーションし、その確率密度の形状を確認するとともに、期待値がどのようになるか確かめます。
をシミュレーションし、その確率密度の形状を確認するとともに、期待値がどのようになるか確かめます。
# 2014 Q2(5) 2024.1.4
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
n_simulations = 10**6 # サンプルサイズ
n = 5 # サンプルサイズ (n個の確率変数)
# 一様分布からサンプリング
U = np.random.uniform(0, 1, (n_simulations, n))
# PDF (確率密度関数) および期待値をプロット
j_values = range(1, n + 1) # j を 1 から n まで変化させる
plt.figure(figsize=(14, 8))
colors = ['blue', 'orange', 'green', 'red', 'purple'] # 色の設定
for idx, j in enumerate(j_values):
# j 番目の順序統計量を取得
U_j = np.sort(U, axis=1)[:, j-1]
# 理論値のPDFを計算
u = np.linspace(0, 1, 1000)
pdf_theory = (n * np.math.comb(n-1, j-1)) * (u**(j-1)) * ((1-u)**(n-j))
# ヒストグラム (シミュレーション結果)
plt.hist(U_j, bins=50, density=True, alpha=0.5, label=f'j = {j} (シミュレーション)', color=colors[idx])
# 理論値のPDFをプロット
plt.plot(u, pdf_theory, linestyle='--', color=colors[idx], label=f'j = {j} (理論)')
# 理論値の期待値を直線で追加
expected_value = j / (n + 1)
plt.axvline(x=expected_value, color=colors[idx], linestyle=':', label=f'j = {j} 期待値 = {expected_value:.2f}')
# グラフ装飾
plt.title('順序統計量 U_(j) の PDF と期待値 (理論 vs シミュレーション)', fontsize=16)
plt.xlabel('値', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()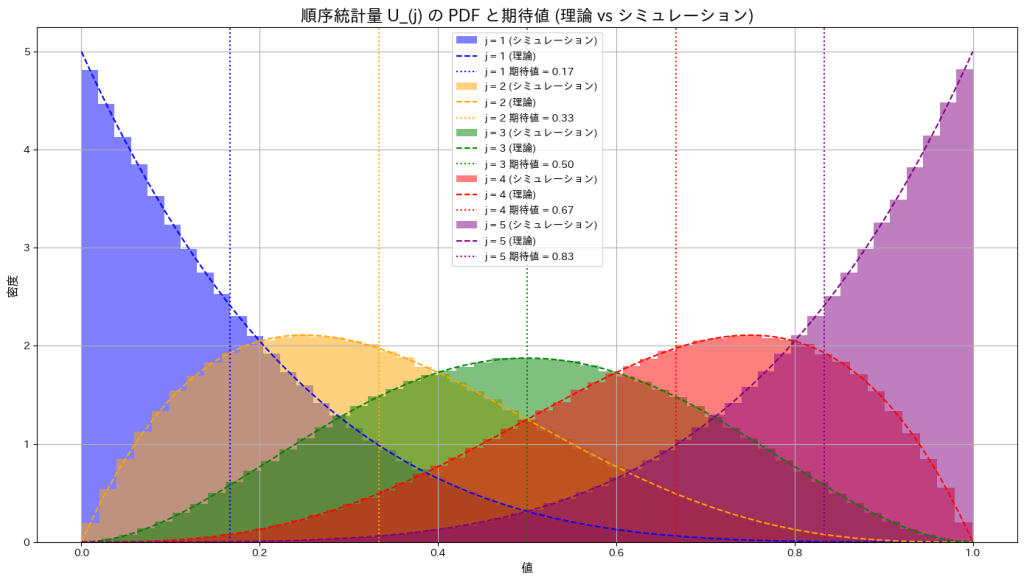
一様分布の順序統計量![]() の確率密度は、jが小さいときには左に寄り、jが大きくなると右に寄る形状を示します。また期待値はj/(n+1)であるため0~1の範囲をn+1で均等に分割した値に一致することが確認できました。
の確率密度は、jが小さいときには左に寄り、jが大きくなると右に寄る形状を示します。また期待値はj/(n+1)であるため0~1の範囲をn+1で均等に分割した値に一致することが確認できました。
2014 Q2(4)
n個の一様分布の順序統計量の同時分布が、前問の分布に等しい事を示しました。

コード
![]() と
と![]() の個別の分布をシミュレーションし、グラフを描画してみます。
の個別の分布をシミュレーションし、グラフを描画してみます。
# 2014 Q2(4) 2025.1.3
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 5 # 次元数
num_samples = 10000 # サンプル数
# (1) ガンマ分布からサンプルを生成して X_1, ..., X_(n+1) を計算
X = np.random.gamma(shape=1, scale=1, size=(num_samples, n+1)) # ガンマ分布からサンプル生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_(n+1)
# (2) Y_1, ..., Y_n を計算 (累積和を利用)
cumulative_sum_X = np.cumsum(X[:, :-1], axis=1) # 累積和 (X_1, X_1 + X_2, ..., X_1 + ... + X_n)
Y = cumulative_sum_X / T[:, None] # Y_i = (X_1 + ... + X_i) / T
# (3) 一様分布から順序統計量を生成
U = np.sort(np.random.uniform(0, 1, size=(num_samples, n)), axis=1) # 順序統計量 U_(1), ..., U_(n)
# (4) 個別の分布を比較
plt.figure(figsize=(12, 6))
for i in range(n):
plt.hist(Y[:, i], bins=50, alpha=0.5, density=True, label=rf"$Y_{i+1}$", histtype='step', linewidth=2)
plt.hist(U[:, i], bins=50, alpha=0.5, density=True, label=rf"$U_{{({i+1})}}$", histtype='step', linestyle='--', linewidth=2)
# グラフの装飾
plt.title("累積比率と順序統計量の個別分布の比較", fontsize=16)
plt.xlabel("値", fontsize=14)
plt.ylabel("確率密度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()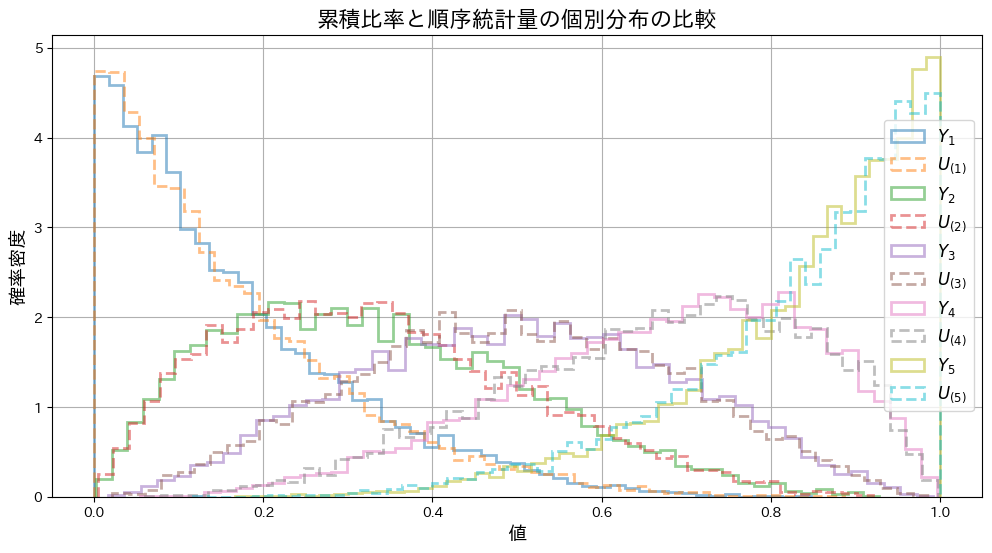
![]() と
と![]() の分布の形状は重なり、一致していることが確認できました。
の分布の形状は重なり、一致していることが確認できました。
次に、同時確率![]() と
と![]() の分布をシミュレーションし、グラフを描画してみます。
の分布をシミュレーションし、グラフを描画してみます。
# 2014 Q2(4) 2025.1.3
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 5 # 次元数
num_samples = 10000 # サンプル数
# (1) ガンマ分布からサンプルを生成して X_1, ..., X_(n+1) を計算
X = np.random.gamma(shape=1, scale=1, size=(num_samples, n+1)) # ガンマ分布からサンプル生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_(n+1)
# (2) Y_1, ..., Y_n を計算 (累積和を利用)
cumulative_sum_X = np.cumsum(X[:, :-1], axis=1) # 累積和 (X_1, X_1 + X_2, ..., X_1 + ... + X_n)
Y = cumulative_sum_X / T[:, None] # Y_i = (X_1 + ... + X_i) / T
# (3) 一様分布から順序統計量を生成
U = np.sort(np.random.uniform(0, 1, size=(num_samples, n)), axis=1) # 順序統計量 U_(1), ..., U_(n)
# (4) 同時確率密度を計算
cumulative_density = np.prod(Y, axis=1) # 累積比率 (Y_1 * Y_2 * ... * Y_n)
order_stats_density = np.prod(U, axis=1) # 順序統計量 (U_(1) * U_(2) * ... * U_(n))
# (5) ヒストグラムを描画して比較
plt.figure(figsize=(12, 6))
# 累積比率分布の同時確率密度
plt.hist(cumulative_density, bins=50, alpha=0.5, density=True, label=r"$f_Y(Y_1, Y_2, \ldots, Y_n)$")
# 順序統計量の同時確率密度
plt.hist(order_stats_density, bins=50, alpha=0.5, density=True, label=r"$f_U(U_{(1)}, U_{(2)}, \ldots, U_{(n)})$")
# グラフの装飾
plt.title("累積比率分布と順序統計量の同時確率密度の比較", fontsize=16)
plt.xlabel("同時確率密度", fontsize=14)
plt.ylabel("頻度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()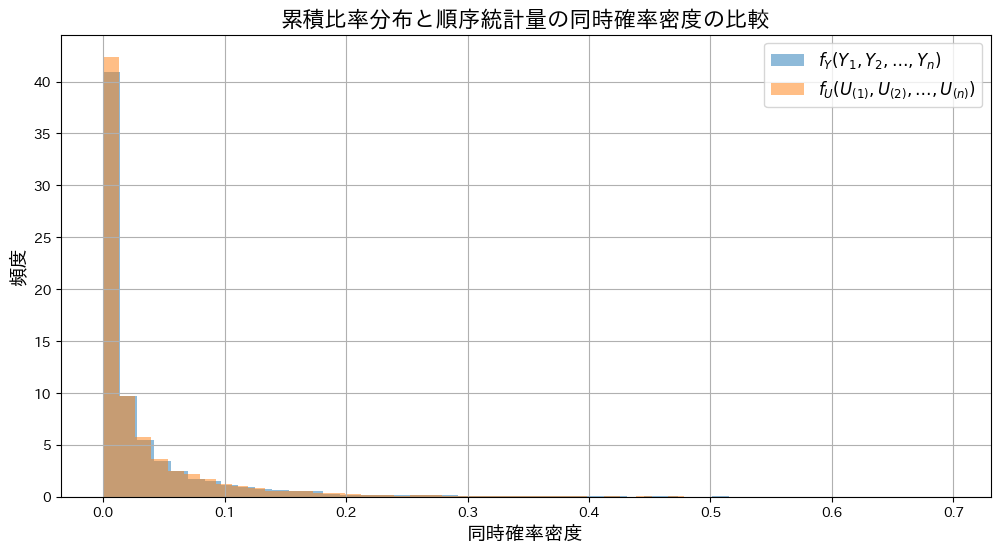
同時確率![]() と
と![]() の分布の形状は重なり、一致していることが確認できました。
の分布の形状は重なり、一致していることが確認できました。
2014 Q2(3)
形状パラメータが1のガンマ分布は指数分布となり、その和はガンマ分布に従うことを示しました。

コード
TとYの分布についてシミュレーションを行い、それらの形状を視覚化して確認します。
# 2014 Q2(3) 2024.1.2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
n = 5 # n+1 個のガンマ分布の和
num_samples = 10000 # シミュレーション回数
# ガンマ分布から乱数を生成
X = gamma.rvs(a=1, scale=1, size=(num_samples, n+1)) # 各行に n+1 個のガンマ乱数を生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_{n+1}
# 修正: Y を累積比率で計算
cumulative_sum_X = np.cumsum(X[:, :-1], axis=1) # X_1, X_1 + X_2, ..., X_1 + ... + X_n
Y = cumulative_sum_X / T[:, None] # Y_i = (X_1 + ... + X_i) / T
# T のヒストグラムを描画
plt.figure(figsize=(10, 6))
t_values = np.linspace(0, 30, 1000)
plt.hist(T, bins=50, density=True, alpha=0.6, color="blue", label="シミュレーション (T)")
plt.plot(t_values, gamma.pdf(t_values, a=n+1, scale=1), color="red", label=f"理論分布 (Gamma({n+1}, 1))")
plt.title("$T$ の分布", fontsize=16)
plt.xlabel("$T$", fontsize=14)
plt.ylabel("確率密度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()
# Y の確認 (サンプルの分布)
plt.figure(figsize=(10, 6))
for i in range(n):
plt.hist(Y[:, i], bins=50, density=True, alpha=0.5, label=f"$Y_{i+1}$")
plt.title("$Y$ の分布 (各比率)", fontsize=16)
plt.xlabel("$Y_i$", fontsize=14)
plt.ylabel("確率密度", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()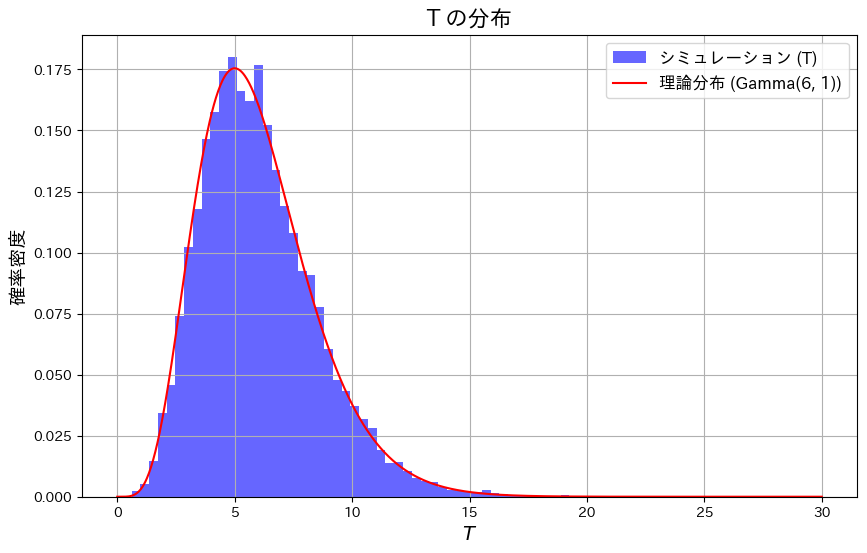
TがGa(n+1,1)のガンマ分布と一致することを確認しました。
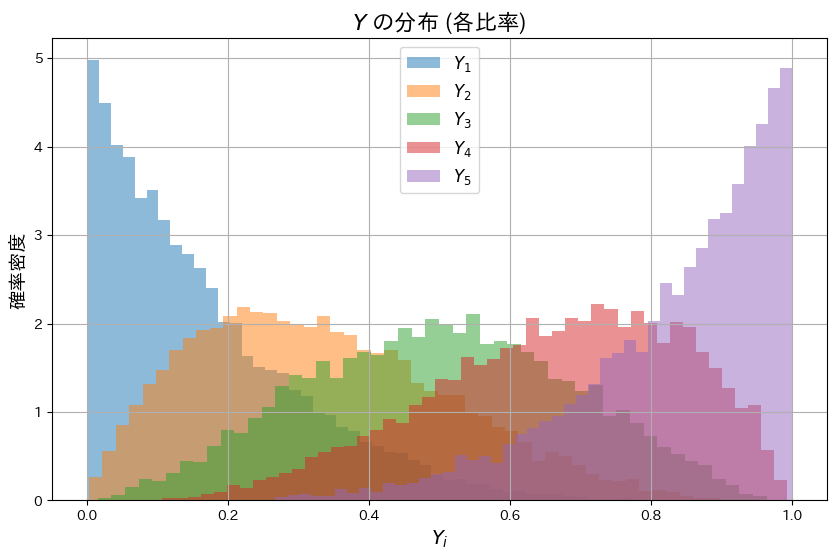
各Yiは累積比率として定義されているため、順序性(Y1<Y2<..<Yn)を持つように見えます。
次に、YiとTが独立であることを確認するため、散布図を描画し、それぞれの共分散Cov(Yi, T)を算出します。
# 2014 Q2(3) 2024.1.2
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
n = 5 # n+1 個のガンマ分布の和
num_samples = 10000 # シミュレーション回数
# ガンマ分布から乱数を生成
X = gamma.rvs(a=1, scale=1, size=(num_samples, n+1)) # 各行に n+1 個のガンマ乱数を生成
T = X.sum(axis=1) # T = X_1 + X_2 + ... + X_{n+1}
Y = X[:, :-1] / T[:, None] # Y_i = X_i / T (最後の列を除いて正規化)
# (1) 共分散の計算
print("各 Y_i と T の共分散:")
for i in range(n):
cov = np.cov(Y[:, i], T)[0, 1] # 共分散行列から共分散を取得
print(f"Cov(Y_{i+1}, T) = {cov:.5f}")
# (2) 散布図の描画
plt.figure(figsize=(12, 8))
for i in range(n):
plt.scatter(T, Y[:, i], alpha=0.3, label=f"$Y_{i+1}$ vs $T$")
plt.title("散布図: 各 $Y_i$ と $T$ の関係", fontsize=16)
plt.xlabel("$T$", fontsize=14)
plt.ylabel("$Y_i$", fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()各 Y_i と T の共分散:
Cov(Y_1, T) = 0.00426
Cov(Y_2, T) = 0.00394
Cov(Y_3, T) = -0.00261
Cov(Y_4, T) = -0.00364
Cov(Y_5, T) = -0.00399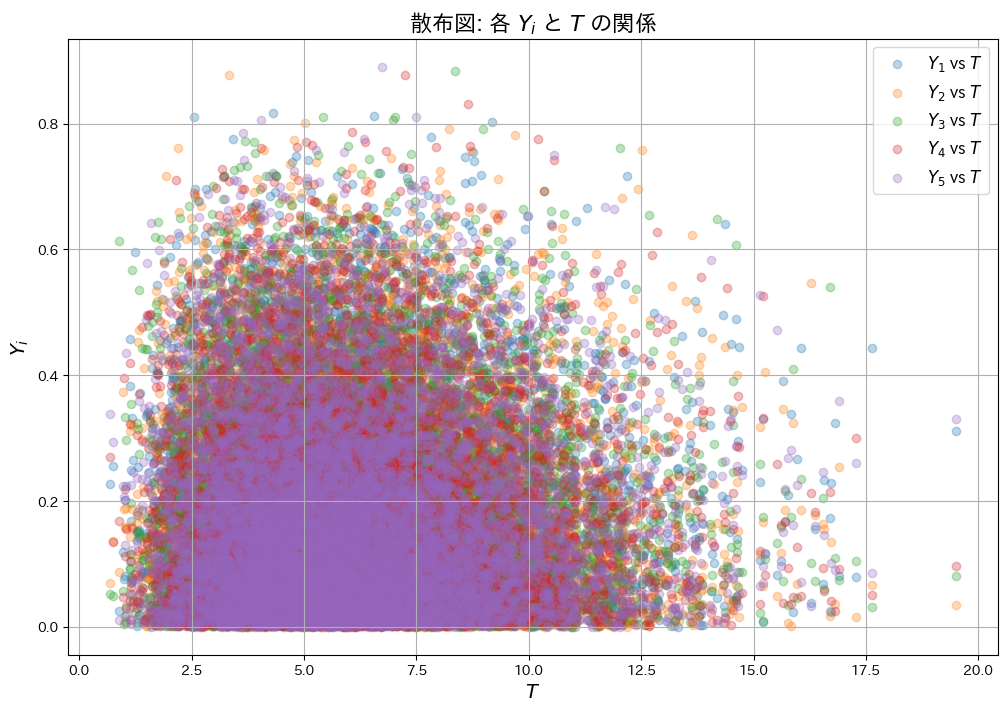
それぞれの共分散Cov(Yi, T)はほぼ0を示し、散布図からもYiとTが互いに影響を与えていないことが確認できました。