ホーム » 信頼区間推定
「信頼区間推定」カテゴリーアーカイブ
2014 Q3(2)
液体のサンプルの体積と重さから得た比重βがβ0であるという帰無仮説が棄却されないβの信頼区間を体積と重さの分散が未知の場合で求めました。

コード
分散未知の場合の信頼区間をシミュレーションし、カバー率が理論値(1 – α = 0.95)に一致するかを検証してみます。
# 2014 Q3(2) 2025.1.7
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t
# Parameters
n = 30 # サンプルサイズ
beta_true = 1.5 # 真のβ
sigma_X = 1.0 # Xの標準偏差
sigma_Y = 3.0 # Yの標準偏差
mu_X = 5.0 # Xの平均
alpha = 0.05 # 有意水準
num_simulations = 100 # シミュレーション回数
# 分散未知の場合の信頼区間を計算する関数
def confidence_interval_unknown_variance(X, Y, beta_0, alpha):
X_bar = np.mean(X)
Y_bar = np.mean(Y)
U = Y - beta_0 * X
S_square = np.sum((U - np.mean(U))**2) / (n - 1) # 標本分散
S_star = np.sqrt(S_square)
t_alpha = t.ppf(1 - alpha / 2, df=n - 1)
lower_bound = Y_bar / X_bar - t_alpha * S_star / (np.sqrt(n) * X_bar)
upper_bound = Y_bar / X_bar + t_alpha * S_star / (np.sqrt(n) * X_bar)
return lower_bound, upper_bound
# シミュレーション
intervals_unknown = []
contains_true_beta_unknown = []
for _ in range(num_simulations):
X = np.random.normal(mu_X, sigma_X, n)
epsilon = np.random.normal(0, np.sqrt(sigma_Y**2 + (beta_true * sigma_X)**2), n)
Y = beta_true * X + epsilon
# 信頼区間を計算
ci = confidence_interval_unknown_variance(X, Y, beta_true, alpha)
intervals_unknown.append(ci)
contains_true_beta_unknown.append(ci[0] <= beta_true <= ci[1])
# カバー率を計算
cover_rate_unknown = sum(contains_true_beta_unknown) / num_simulations
print("カバー率:")
print(f" 分散未知の場合: {cover_rate_unknown:.4f}")
# 可視化
plt.figure(figsize=(12, 8))
for i, ci in enumerate(intervals_unknown):
color = 'green' if contains_true_beta_unknown[i] else 'red'
plt.plot([ci[0], ci[1]], [i, i], color=color, marker='o', label="" if i > 0 else "信頼区間")
plt.axvline(x=beta_true, color='blue', linestyle='--', label=f"真のβ: {beta_true}")
plt.title("分散未知の場合の信頼区間 (各シミュレーション)", fontsize=16)
plt.xlabel("β", fontsize=12)
plt.ylabel("シミュレーション回数", fontsize=12)
plt.legend()
plt.grid()
plt.show()カバー率:
分散未知の場合: 0.9500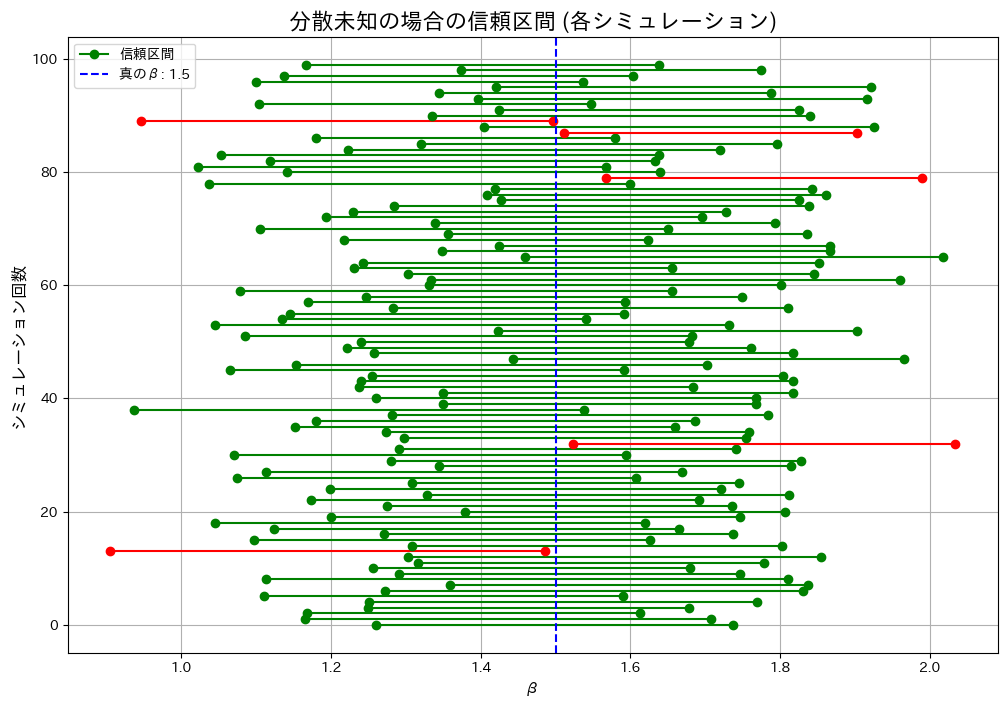
実行ごとに値は変動しましたが、カバー率は概ね理論値(1 – α = 0.95)に一致しました。
2014 Q3(2)
液体のサンプルの体積と重さから得た比重βがβ0であるという帰無仮説が棄却されないβの信頼区間を体積と重さの分散が既知の場合で求めました。

コード
分散既知の場合の信頼区間をシミュレーションし、カバー率が理論値(1 – α = 0.95)に一致するかを検証してみます。
# 2014 Q3(2) 2025.1.6
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters
n = 30 # サンプルサイズ
beta_true = 1.5 # 真のβ
sigma_X = 1.0 # Xの標準偏差
sigma_Y = 3.0 # Yの標準偏差
mu_X = 5.0 # Xの平均
alpha = 0.05 # 有意水準
num_simulations = 100 # シミュレーション回数
# 分散既知の場合の信頼区間計算関数
def precise_confidence_interval(X, Y, sigma_X, sigma_Y, alpha):
X_bar = np.mean(X)
Y_bar = np.mean(Y)
z_alpha = norm.ppf(1 - alpha / 2)
numerator = n * X_bar * Y_bar
term1 = (n * X_bar * Y_bar)**2
term2 = (n * X_bar**2 - z_alpha**2 * sigma_X**2)
term3 = (n * Y_bar**2 - z_alpha**2 * sigma_Y**2)
denominator = n * X_bar**2 - z_alpha**2 * sigma_X**2
if term2 * term3 < 0:
raise ValueError("平方根の中身が負の値です:term2 * term3 は 0 以上でなければなりません。")
sqrt_term = np.sqrt(term1 - term2 * term3)
lower_bound = (numerator - sqrt_term) / denominator
upper_bound = (numerator + sqrt_term) / denominator
return lower_bound, upper_bound
# シミュレーション
intervals_precise = []
contains_true_beta_precise = []
for _ in range(num_simulations):
X = np.random.normal(mu_X, sigma_X, n)
epsilon = np.random.normal(0, np.sqrt(sigma_Y**2 + (beta_true * sigma_X)**2), n)
Y = beta_true * X + epsilon
# 信頼区間を計算
ci = precise_confidence_interval(X, Y, sigma_X, sigma_Y, alpha)
intervals_precise.append(ci)
contains_true_beta_precise.append(ci[0] <= beta_true <= ci[1])
# カバー率を計算
cover_rate_precise = sum(contains_true_beta_precise) / num_simulations
print("カバー率:")
print(f" 分散既知の場合: {cover_rate_precise:.4f}")
# 可視化
plt.figure(figsize=(12, 8))
for i, ci in enumerate(intervals_precise):
color = 'green' if contains_true_beta_precise[i] else 'red'
plt.plot([ci[0], ci[1]], [i, i], color=color, marker='o', label="" if i > 0 else "信頼区間")
plt.axvline(x=beta_true, color='blue', linestyle='--', label=f"真のβ: {beta_true}")
plt.title("分散既知の場合の信頼区間 (各シミュレーション)", fontsize=16)
plt.xlabel("β", fontsize=12)
plt.ylabel("シミュレーション回数", fontsize=12)
plt.legend()
plt.grid()
plt.show()カバー率:
分散既知の場合: 0.9500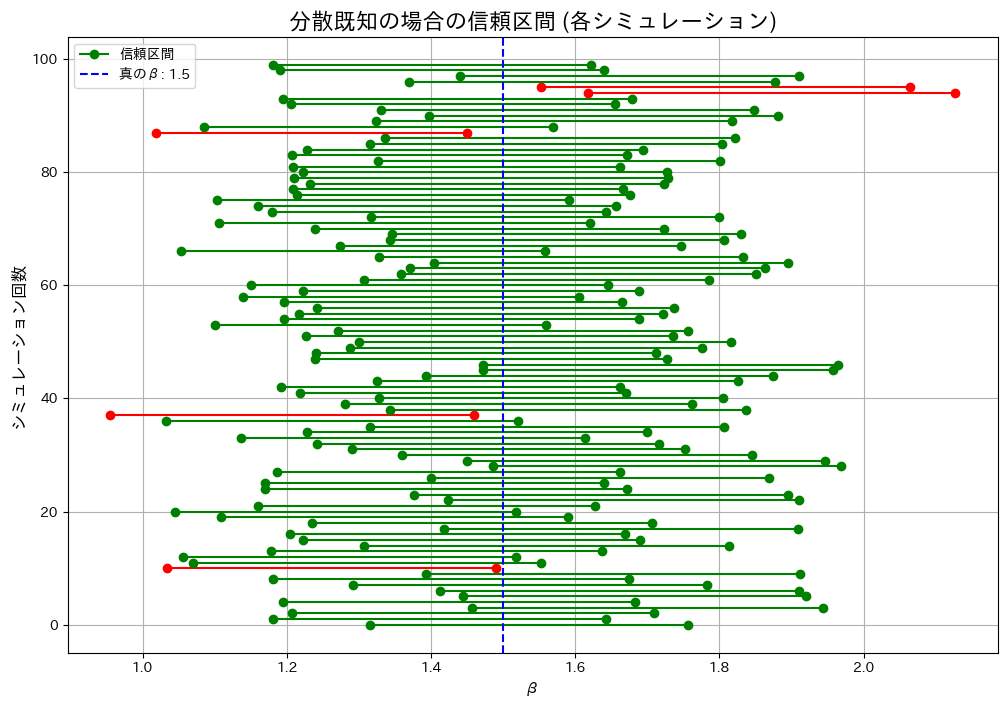
実行ごとに値は変動しましたが、カバー率は概ね理論値(1 – α = 0.95)に一致しました。
2021 Q3(4)
ポアソン分布のパラメータλの区間推定の中点がその最尤推定値より大きくなることを学びました。面白い。

コード
ポアソン分布の確率質量関数にλに3,5,10を与えてプロットします
#2021 Q3(4) 2024.8.30
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# パラメータ設定
lambda_values = [3, 5, 10] # 異なる λ の値
max_x = 25 # x軸の最大値(PMFの表示範囲)
# プロットの設定
plt.figure(figsize=(12, 6))
# 各 λ について PMF を計算し、プロット
for lambda_value in lambda_values:
x = np.arange(0, max_x + 1) # x軸の範囲
pmf = poisson.pmf(x, lambda_value) # PMF を計算
plt.plot(x, pmf, marker='o', label=f'λ = {lambda_value}')
# グラフの装飾
plt.title('ポアソン分布の確率質量関数(PMF)の比較')
plt.xlabel('x')
plt.ylabel('P(X=x)')
plt.legend()
plt.grid(True)
plt.show()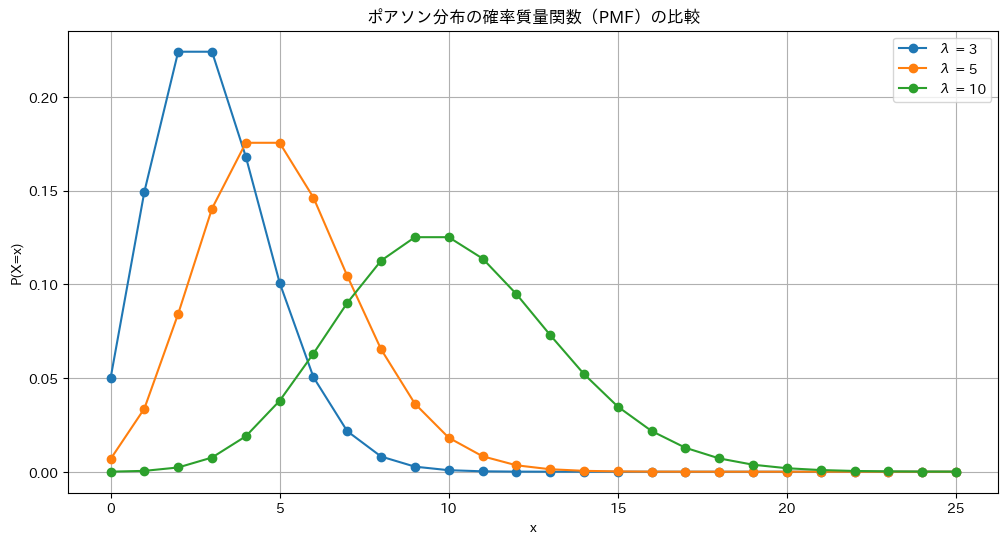
λが大きくなるほど分散も大きくなります
λの信頼区間と最尤推定値の関係を見てみます
#2021 Q3(4) 2024.8.30
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
lambda_true = 5 # 真の λ の値
n = 10 # サンプル数
num_simulations = 1000 # シミュレーション回数
# 信頼区間と最尤推定値の保存リスト
lambda_L_values = []
lambda_U_values = []
lambda_hat_values = []
# シミュレーション開始
for _ in range(num_simulations):
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_true, n)
T = np.sum(samples) # T を計算
# 最尤推定値を計算
lambda_hat = T / n
# 信頼区間の計算
lambda_L = (T - 2*np.sqrt(T + 1) + 2) / n
lambda_U = (T + 2*np.sqrt(T + 1) + 2) / n
# 結果を保存
lambda_L_values.append(lambda_L)
lambda_U_values.append(lambda_U)
lambda_hat_values.append(lambda_hat)
# 信頼区間の中点の計算
lambda_M_values = [(lambda_L_values[i] + lambda_U_values[i]) / 2 for i in range(num_simulations)]
lambda_M_mean = np.mean(lambda_M_values)
# 最尤推定値の平均を計算
lambda_hat_mean = np.mean(lambda_hat_values)
# 信頼区間のプロット
plt.figure(figsize=(12, 6))
for i in range(num_simulations):
plt.plot([lambda_L_values[i], lambda_U_values[i]], [i, i], color='blue')
plt.axvline(lambda_hat_mean, color='purple', linestyle='--', label='最尤推定値の平均')
plt.axvline(lambda_M_mean, color='orange', linestyle='-', label='信頼区間の中点の平均')
plt.title('信頼区間と最尤推定値の関係')
plt.xlabel('λ の値')
plt.ylabel('シミュレーション回数')
plt.legend()
plt.grid(True)
plt.show()
# 中点の平均値を表示
print(f'信頼区間の中点の平均: {lambda_M_mean:.4f}')
print(f'最尤推定値の平均: {lambda_hat_mean:.4f}')
print(f'真の λ: {lambda_true}')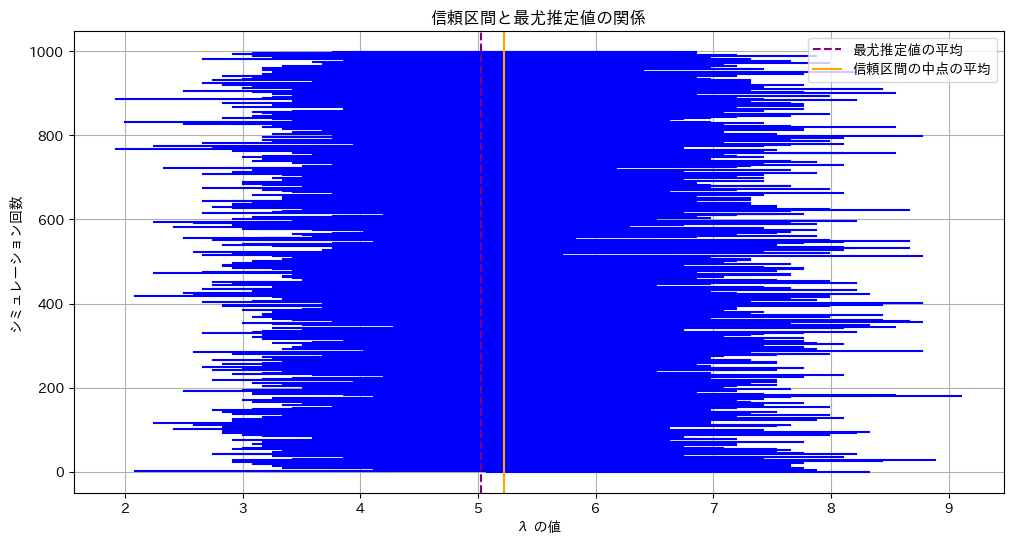
信頼区間の中点の平均: 5.2235
最尤推定値の平均: 5.0235
真の λ: 5λの信頼区間の中点は最尤推定値よりも右にずれます。λが大きくなると分散が大きくなるためです。
X=5に固定したポアソン分布の確率質量関数P(X=5|λ)のグラフを見てみます
#2021 Q3(4) 2024.8.30
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# パラメータ設定
x_value = 5 # 固定された x の値
n = 10 # サンプル数(ここでは仮に10個の観測データがあると仮定)
T = x_value * n # 合計値 T は x * n として計算
# λの範囲を指定
lambda_range = np.linspace(1, 20, 200)
# λに対するPMFを計算
pmf_values = poisson.pmf(x_value, lambda_range)
# 最尤推定値(λ_hat)を計算
lambda_hat = T / n
# 信頼区間の計算
lambda_L = (T - 2*np.sqrt(T + 1) + 2) / n
lambda_U = (T + 2*np.sqrt(T + 1) + 2) / n
lambda_M = (lambda_L + lambda_U) / 2 # 信頼区間の中点
# グラフの描画
plt.figure(figsize=(12, 6))
plt.plot(lambda_range, pmf_values, label=f'P(X={x_value})')
# 最尤推定値、信頼区間の上下限、中点を表示
plt.axvline(lambda_hat, color='red', linestyle='--', label=f'最尤推定値 λ_hat = {lambda_hat:.2f}')
plt.axvline(lambda_L, color='blue', linestyle='--', label=f'信頼区間下限 λ_L = {lambda_L:.2f}')
plt.axvline(lambda_U, color='green', linestyle='--', label=f'信頼区間上限 λ_U = {lambda_U:.2f}')
plt.axvline(lambda_M, color='orange', linestyle='-', label=f'信頼区間中点 λ_M = {lambda_M:.2f}')
# グラフの装飾
plt.title(f'ポアソン分布のPMFと信頼区間の中点(x={x_value}固定)')
plt.xlabel('λ')
plt.ylabel(f'P(X={x_value})')
plt.grid(True)
plt.legend()
plt.show()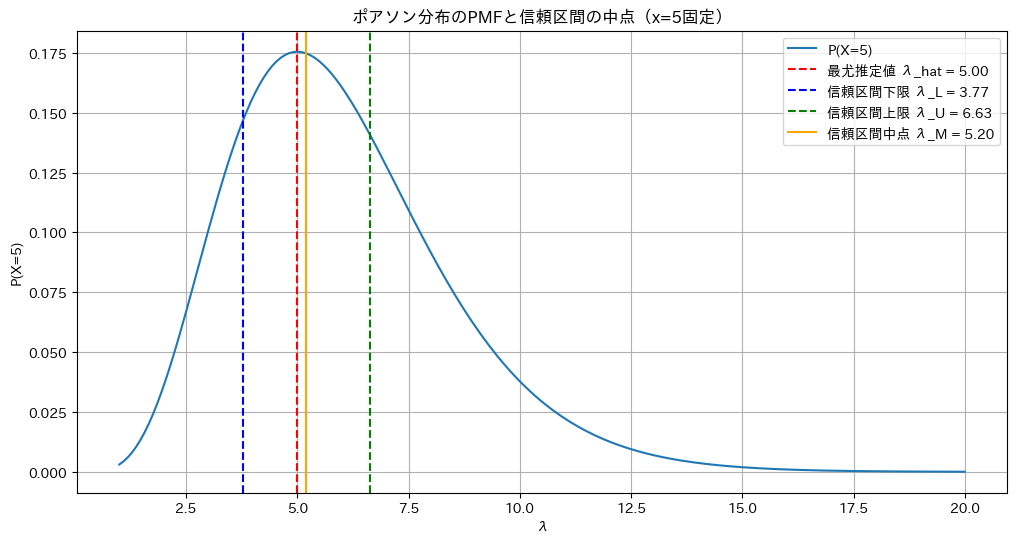
右に裾が長く、λの信頼区間の中点は最尤推定値よりも右にズレていることが分かります。
なお、このグラフは、ボソン分布の確率質量関数
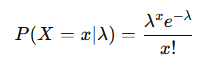
より
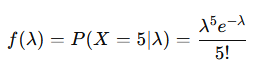
となります。これは、k=6 , θ=1 としたときガンマ分布に一致します
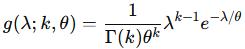
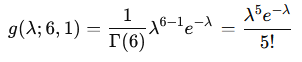
2021 Q3(3)
ポアソン分布に従う複数の確率変数の和が正規分布に近似するとした場合の信頼区間を求める問題を学びました。
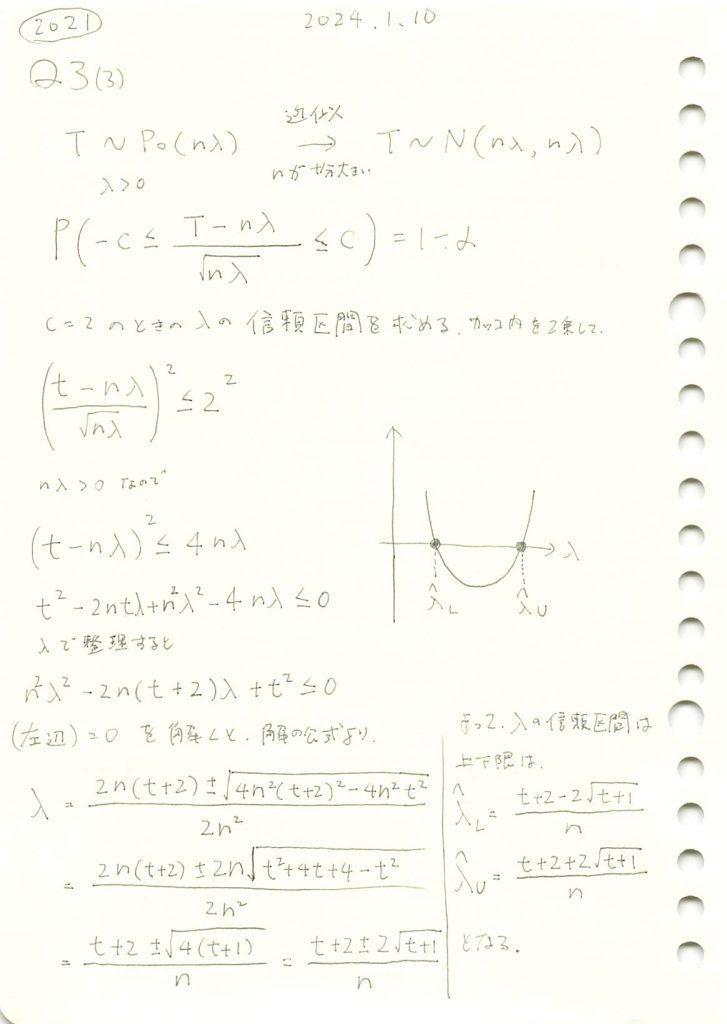
コード
二次方程式を解いて信頼区間を求めます
# 2021 Q3(3) 2024.8.29
import sympy as sp
# 変数の定義
n, lambda_, T = sp.symbols('n lambda_ T', real=True, positive=True)
c = 2
# 不等式を通常の方程式として変換
# まず、二次方程式の形を導出
lhs = sp.Eq((T - n*lambda_)**2, (c**2) * n * lambda_)
# λに関する二次方程式を解く
solutions = sp.solve(lhs, lambda_)
# 解の表示
lambda_L = solutions[0].simplify()
lambda_U = solutions[1].simplify()
# 結果の表示
display(lambda_L, lambda_U)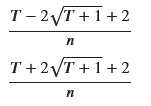
シミュレーションで、真のλが信頼区間に含まれる割合を求めます
# 2021 Q3(3) 2024.8.29
import numpy as np
# パラメータの設定
lambda_true = 5 # 真の λ の値
n = 10 # サンプル数
num_simulations = 1000 # シミュレーションの回数
# 結果を保存するカウンター
within_confidence = 0
# シミュレーション開始
for _ in range(num_simulations):
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_true, n)
T = np.sum(samples) # T を計算
# 信頼区間の計算
lambda_L = (T - 2*np.sqrt(T + 1) + 2) / n
lambda_U = (T + 2*np.sqrt(T + 1) + 2) / n
# 真のλが信頼区間内にあるか確認
if lambda_L <= lambda_true <= lambda_U:
within_confidence += 1
# 信頼区間内に真のλが含まれる割合を計算
coverage = within_confidence / num_simulations
# 結果の表示
print(f"{num_simulations}回のシミュレーションのうち、真のλが信頼区間内に含まれていた割合: {coverage:.4f}")1000回のシミュレーションのうち、真のλが信頼区間内に含まれていた割合: 0.9550c=2のとき信頼区間の信頼率は95.45%となり、シミュレーションと概ね一致します
上のシミュレーションを視覚化します
# 2021 Q3(3) 2024.8.29
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
lambda_true = 5 # 真の λ の値
n = 10 # サンプル数
num_simulations = 1000 # シミュレーションの回数
# 結果を保存するリスト
lower_limits = []
upper_limits = []
within_confidence = 0
# シミュレーション開始
for _ in range(num_simulations):
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_true, n)
T = np.sum(samples) # T を計算
# 信頼区間の計算
lambda_L = (T - 2*np.sqrt(T + 1) + 2) / n
lambda_U = (T + 2*np.sqrt(T + 1) + 2) / n
# 信頼区間の記録
lower_limits.append(lambda_L)
upper_limits.append(lambda_U)
# 真のλが信頼区間内にあるか確認
if lambda_L <= lambda_true <= lambda_U:
within_confidence += 1
# 信頼区間内に真のλが含まれる割合を計算
coverage = within_confidence / num_simulations
print(f"{num_simulations}回のシミュレーションのうち、真のλが信頼区間内に含まれていた割合: {coverage:.4f}")
# ヒストグラムのプロット
plt.figure(figsize=(12, 6))
plt.hist(lower_limits, bins=30, alpha=0.5, label='信頼区間の下限', color='blue')
plt.hist(upper_limits, bins=30, alpha=0.5, label='信頼区間の上限', color='red')
plt.axvline(lambda_true, color='green', linestyle='--', label='真の λ')
plt.title('信頼区間の分布')
plt.xlabel('λ の値')
plt.ylabel('頻度')
plt.legend()
plt.grid(True)
plt.show()
# 信頼区間のプロット
plt.figure(figsize=(12, 6))
for i in range(num_simulations):
plt.plot([lower_limits[i], upper_limits[i]], [i, i], color='blue')
plt.axvline(lambda_true, color='red', linestyle='--', label='真の λ')
plt.title('シミュレーションごとの信頼区間')
plt.xlabel('λ の値')
plt.ylabel('シミュレーション回数')
plt.legend()
plt.grid(True)
plt.show()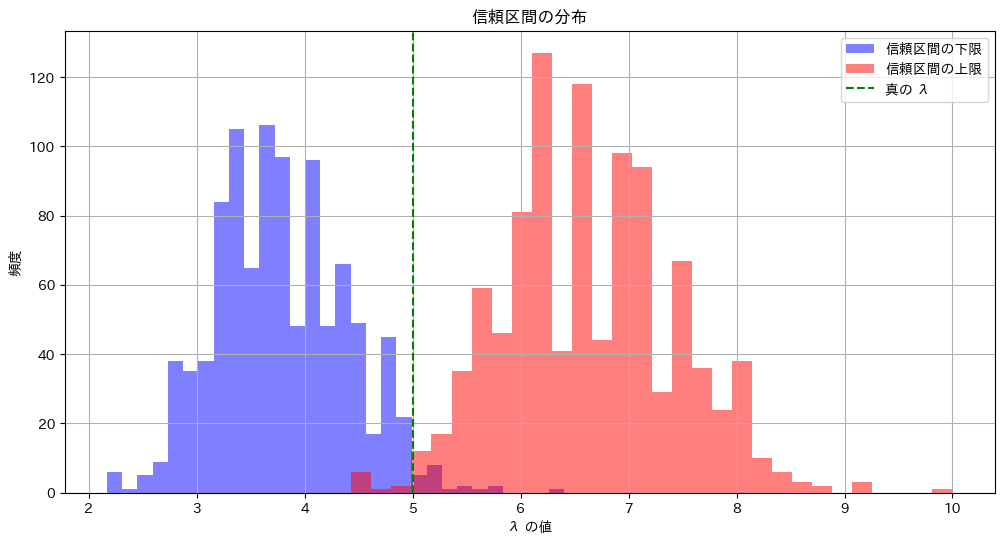
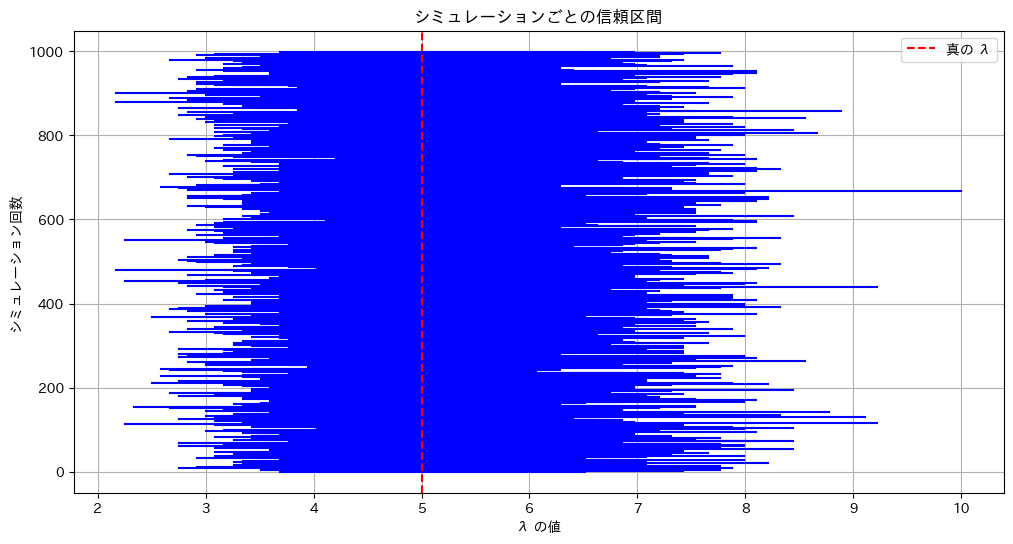
真のλが95.45%の確率で信頼区間内に含まれている様子が確認できました。