ホーム » コードあり (ページ 9)
「コードあり」カテゴリーアーカイブ
2017 Q2(2)
標本平均の2倍が一様分布の上限値の不偏推定量であることの証明をしました。

コード
θ=10,n=20としてシミュレーションを行い、θ’の分布を見てみます。
# 2017 Q2(2) 2024.10.30
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
theta_true = 10 # 真の θ の値
n = 20 # 1試行あたりのサンプル数
num_trials = 1000 # シミュレーションの試行回数
# シミュレーションを実行
theta_prime_estimates = []
for _ in range(num_trials):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプル平均 X̄ を計算し、それを用いて θ' を計算
theta_prime = 2 * np.mean(samples)
theta_prime_estimates.append(theta_prime)
# θ' の分布をヒストグラムで表示
plt.hist(theta_prime_estimates, bins=30, edgecolor='black', density=True)
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'$\theta\' = 2\bar{X}$')
plt.ylabel('密度')
plt.title(r'$\theta\' = 2\bar{X}$ の分布')
plt.legend()
plt.show()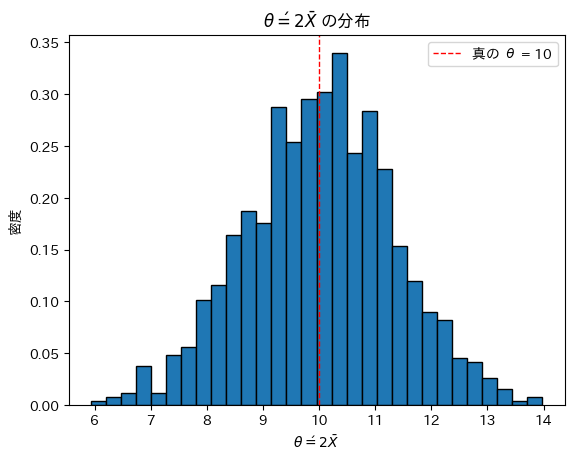
θ’は真のθを中心に左右対称にバラついています。θ’は不偏であるように見えます。
次にサンプルサイズnを変化させて不偏推定量θ’がどうなるのか確認をします。
# 2017 Q2(2) 2024.10.30
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
max_n = 100 # 最大サンプルサイズ
num_trials_per_n = 100 # 各サンプルサイズでの試行回数
# 各サンプルサイズにおける θ' の平均を記録
theta_prime_means = []
# サンプルサイズ n を 1 から max_n まで増やしながらシミュレーション
for n in range(1, max_n + 1):
theta_prime_estimates = []
for _ in range(num_trials_per_n):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプル平均 X̄ を計算し、それを用いて θ' を計算
theta_prime = 2 * np.mean(samples)
theta_prime_estimates.append(theta_prime)
# 各 n に対する θ' の平均を保存
theta_prime_means.append(np.mean(theta_prime_estimates))
# グラフ描画
plt.plot(range(1, max_n + 1), theta_prime_means, label=r'$\mathbb{E}[\theta\']$')
plt.axhline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'サンプルサイズ $n$')
plt.ylabel(r'推定量 $\theta\' = 2 \bar{X}$ の平均')
plt.title(r'サンプルサイズ $n$ と $\theta\' = 2 \bar{X}$ の関係')
plt.legend()
plt.show()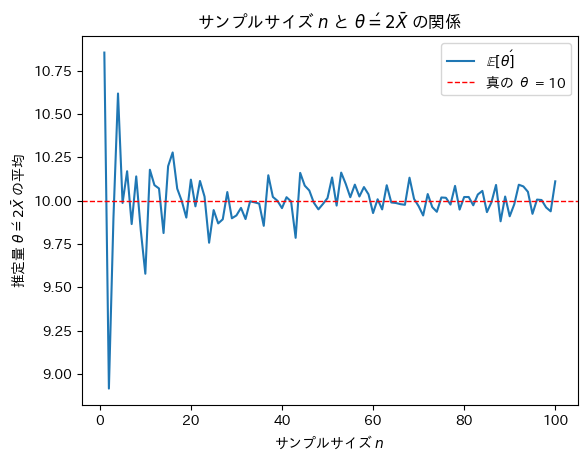
サンプルサイズnが増加するにつれて不偏推定量θ’は真のθに近づくことが確認できました。
2017 Q2(1)
一様分布の上限の最尤推定量を求めました。

コード
θ=10,n=20としてシミュレーションを行い、![]() の分布を見てみます。
の分布を見てみます。
# 2017 Q2(1) 2024.10.29
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
theta_true = 10 # 真の θ の値
n = 20 # 1試行あたりのサンプル数
num_trials = 1000 # シミュレーションの試行回数
# シミュレーションを実行
theta_estimates = []
for _ in range(num_trials):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプルの最大値を推定値 θ_hat として記録
theta_hat = np.max(samples)
theta_estimates.append(theta_hat)
# 推定値の分布をヒストグラムで表示
plt.hist(theta_estimates, bins=30, edgecolor='black', density=True)
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'$\hat{\theta}$')
plt.ylabel('密度')
plt.title(r'$\hat{\theta} = X_{\max}$ の分布')
plt.legend()
plt.show()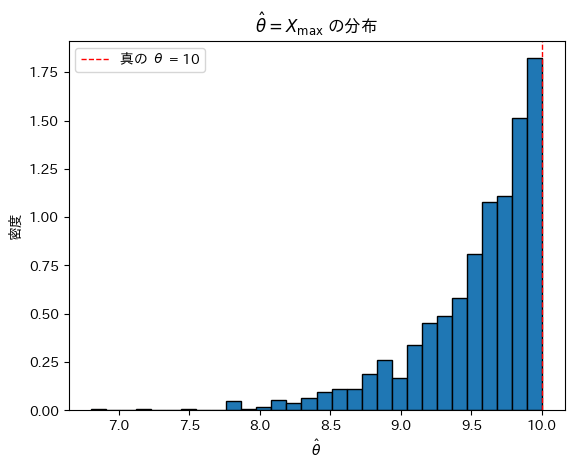
![]() は真のθより大きくならないため、結果としてθよりやや小さな値を取っているように見えます。
は真のθより大きくならないため、結果としてθよりやや小さな値を取っているように見えます。
次にサンプルサイズnを変化させて最尤推定量![]() がどうなるのか確認をします。
がどうなるのか確認をします。
# 2017 Q2(1) 2024.10.29
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真の θ の値
max_n = 100 # 最大サンプルサイズ
num_trials_per_n = 100 # 各サンプルサイズでの試行回数
# 各サンプルサイズにおける θ^ の平均を記録
theta_hat_means = []
# サンプルサイズ n を 1 から max_n まで増やしながらシミュレーション
for n in range(1, max_n + 1):
theta_estimates = []
for _ in range(num_trials_per_n):
# 一様分布 U(0, theta_true) から n 個のサンプルを生成
samples = np.random.uniform(0, theta_true, n)
# サンプルの最大値を推定値 θ_hat として記録
theta_hat = np.max(samples)
theta_estimates.append(theta_hat)
# 各 n に対する θ^ の平均を保存
theta_hat_means.append(np.mean(theta_estimates))
# グラフ描画
plt.plot(range(1, max_n + 1), theta_hat_means, label=r'$\mathbb{E}[\hat{\theta}]$')
plt.axhline(theta_true, color='red', linestyle='dashed', linewidth=1, label=f"真の θ = {theta_true}")
plt.xlabel(r'サンプルサイズ $n$')
plt.ylabel(r'推定量 $\hat{\theta}$ の平均')
plt.title(r'サンプルサイズ $n$ と $\hat{\theta}$ の関係')
plt.legend()
plt.show()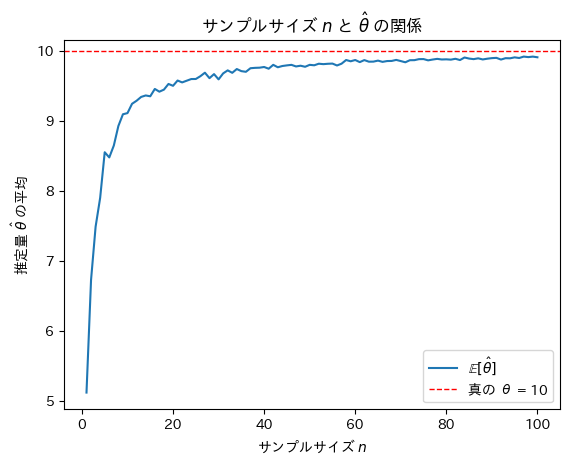
サンプルサイズnが増加するにつれて最尤推定量![]() は真のθに近づくことが確認できました。
は真のθに近づくことが確認できました。
2017 Q1(5)
正規分布の分散の最尤推定量を母平均が既知の場合と未知の場合でそれぞれ求めましまた。

コード
サンプルサイズnを50に固定し尤度関数を可視化します。また最尤推定量 ![]() と
と![]() をプロットしてみます。
をプロットしてみます。
# 2017 Q1(5) 2024.10.28
# 最尤推定量 (T^2, S^2) の計算と尤度関数の可視化
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# シミュレーションパラメータの設定
mu = 5.0 # 母平均(既知)
sigma = 2.0 # 母標準偏差(√母分散)
selected_sample_size = 50 # 固定サンプルサイズ
true_variance = sigma**2 # 母分散
# 正規分布からのサンプル生成(サンプルサイズは selected_sample_size で固定)
sample = np.random.normal(mu, sigma, selected_sample_size) # 固定サンプル生成
# 最尤推定量の計算
T2 = np.sum((sample - mu) ** 2) / selected_sample_size # 最尤推定量 T^2 の計算 (μが既知)
sample_mean = np.mean(sample)
S2 = np.sum((sample - sample_mean) ** 2) / (selected_sample_size - 1) # 最尤推定量 S^2 の計算 (μが未知)
# 尤度関数のプロットのためのパラメータ設定
sigma_squared_trial_values = np.linspace(0.1, 5.0, 100) # σ^2 の値を試行的に設定
likelihoods = [] # 尤度関数の値を保存するリスト
# 尤度関数の計算(固定サンプルに基づく)
for sigma_squared_trial in sigma_squared_trial_values:
likelihood = np.prod(norm.pdf(sample, loc=mu, scale=np.sqrt(sigma_squared_trial))) # 尤度関数の値を計算
likelihoods.append(likelihood)
# グラフの作成
plt.figure(figsize=(10, 6))
plt.plot(sigma_squared_trial_values, likelihoods, label='尤度関数', color='blue')
plt.axvline(x=T2, color='green', linestyle='--', label='$T^2$ (最尤推定量, μが既知)', linewidth=2)
plt.axvline(x=S2, color='orange', linestyle='--', label='$S^2$ (最尤推定量, μが未知)', linewidth=2)
plt.axvline(x=true_variance, color='red', linestyle='-.', label='母分散 $\\sigma^2$', linewidth=2)
plt.title(f'サンプルサイズ {selected_sample_size} における尤度関数と推定量の比較')
plt.xlabel('$\sigma^2$ の試行値')
plt.ylabel('尤度')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()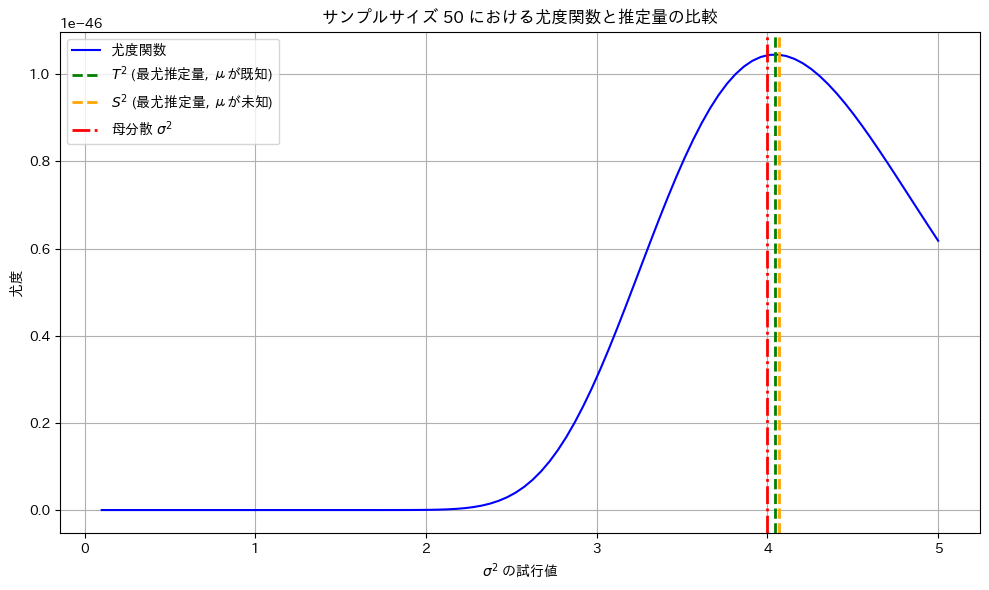
最尤推定量 ![]() と
と![]() は尤度が最大となる
は尤度が最大となる![]() の値を取っています。
の値を取っています。
もう一度実行してみます。
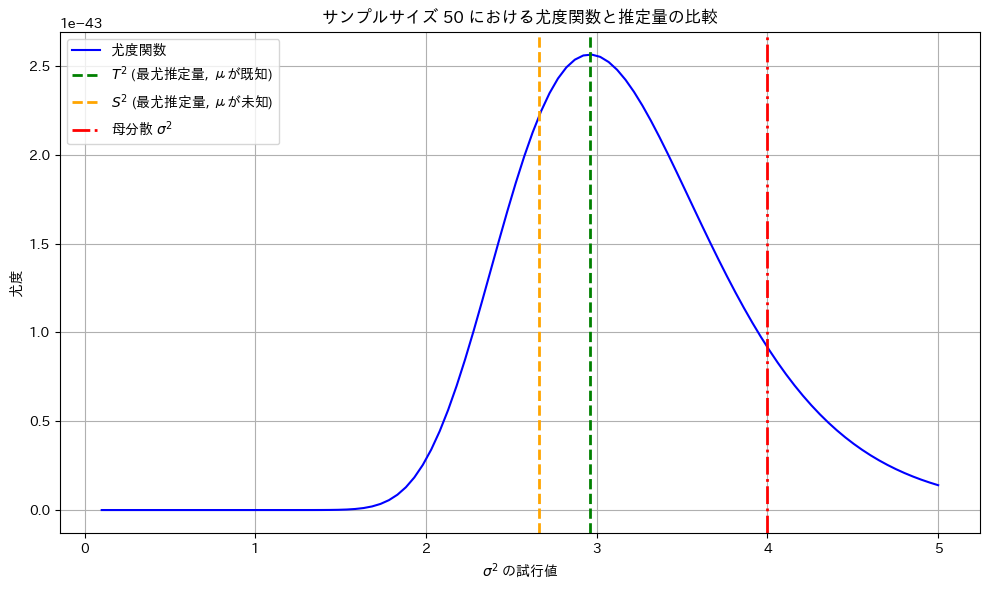
サンプルによっては最尤推定量![]() と
と![]() は
は![]() から乖離する場合もあります。
から乖離する場合もあります。
次に、サンプルサイズを大きくすることで母分散に近づくことを確認します。
# 2017 Q1(5) 2024.10.28
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータの設定
mu = 5.0 # 母平均(既知)
sigma = 2.0 # 母標準偏差(√母分散)
true_variance = sigma**2 # 母分散
sample_sizes = range(50, 10050, 50) # サンプルサイズを設定
# シミュレーション結果を保存するリスト
T2_estimates = [] # μが既知の場合の推定量 T^2
S2_estimates = [] # μが未知の場合の推定量 S^2
# 各サンプルサイズでのシミュレーションの実行
for n in sample_sizes:
# 正規分布からサンプルを抽出
sample = np.random.normal(mu, sigma, n)
# μが既知の場合の最尤推定量 T^2
T2 = np.sum((sample - mu) ** 2) / n
# μが未知の場合の最尤推定量 S^2
sample_mean = np.mean(sample)
S2 = np.sum((sample - sample_mean) ** 2) / (n - 1)
# 推定量をリストに保存
T2_estimates.append(T2)
S2_estimates.append(S2)
# グラフの作成(理論値を追加)
plt.figure(figsize=(12, 8))
# μが既知の場合のプロット (緑)
plt.plot(sample_sizes, T2_estimates, marker='o', color='green', label='$T^2$ (μが既知の場合)', linestyle='--')
# μが未知の場合のプロット (オレンジ)
plt.plot(sample_sizes, S2_estimates, marker='x', color='orange', label='$S^2$ (μが未知の場合)', linestyle='--')
# 理論値の線を追加 (赤)
plt.axhline(y=true_variance, color='red', linestyle='-.', label='理論値: $\sigma^2$', linewidth=2)
# グラフの設定
plt.title('最尤推定量 $T^2$ と $S^2$ のサンプルサイズごとの結果')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('推定量')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()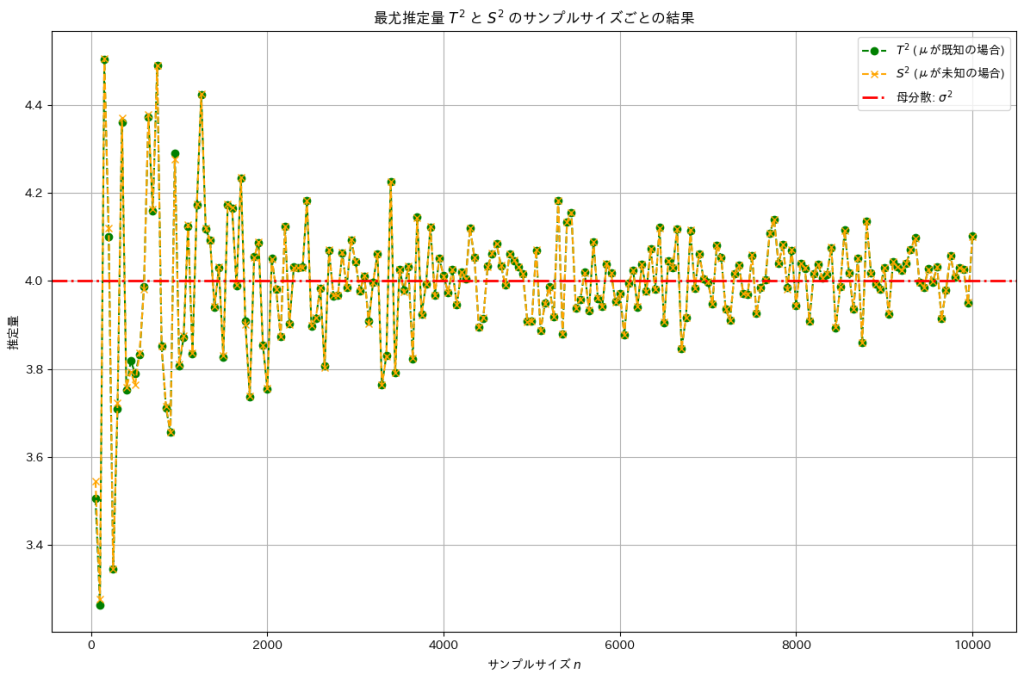
サンプルサイズを大きくすることで最尤推定量![]() と
と![]() は母分散
は母分散![]() に近づきました。
に近づきました。
2017 Q1(4)
サンプル数が十分に大きい時のサンプル平均の歪度と尖度がどのようになるか考察した。

コード
Xの標本平均の歪度と尖度(過剰尖度)はサンプルサイズnが十分大きいときにどう変化するのか確認します。
# 2017 Q1(4) 2024.10.27
from scipy.stats import skew, kurtosis, gamma
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータの設定
#np.random.seed(42) # 再現性のためのシード
num_simulations = 300000 # シミュレーションの繰り返し回数
sample_sizes = range(10, 1100, 50) # サンプルサイズを広げて設定
# 歪度と尖度を持つ母集団分布としてガンマ分布を使用(shape=2で正の歪度と尖度を持つ)
shape_param = 2.0 # ガンマ分布のshapeパラメータ
scale_param = 2.0 # ガンマ分布のscaleパラメータ
population_dist = gamma(a=shape_param, scale=scale_param)
# シミュレーション結果を保存するリスト
sample_mean_skewness = []
sample_mean_kurtosis = []
# 各サンプルサイズでのシミュレーションの実行
for n in sample_sizes:
skew_values = []
kurt_values = []
# シミュレーションを繰り返し
for _ in range(num_simulations):
sample = population_dist.rvs(size=n) # サンプルを抽出
sample_mean = np.mean(sample) # 標本平均
# 標本平均をリストに保存
skew_values.append(sample_mean)
kurt_values.append(sample_mean)
# 標本平均の歪度と尖度を計算
skewness_of_sample_mean = skew(skew_values)
kurtosis_of_sample_mean = kurtosis(kurt_values, fisher=False) - 3 # 過剰尖度に変換
# 結果を保存
sample_mean_skewness.append(skewness_of_sample_mean)
sample_mean_kurtosis.append(kurtosis_of_sample_mean)
# グラフの作成
plt.figure(figsize=(12, 6))
# 歪度のプロット
plt.subplot(1, 2, 1)
plt.plot(sample_sizes, sample_mean_skewness, marker='o', label='歪度')
plt.axhline(y=0, color='r', linestyle='--', label='理論値: 0')
plt.title('サンプルサイズと歪度の関係')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('歪度 ($\\bar{X}$)')
plt.legend()
plt.grid(True)
# 尖度のプロット
plt.subplot(1, 2, 2)
plt.plot(sample_sizes, sample_mean_kurtosis, marker='o', label='尖度(過剰尖度)')
plt.axhline(y=0, color='r', linestyle='--', label='理論値: 0')
plt.title('サンプルサイズと尖度の関係')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('尖度 ($\\bar{X}$)')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()
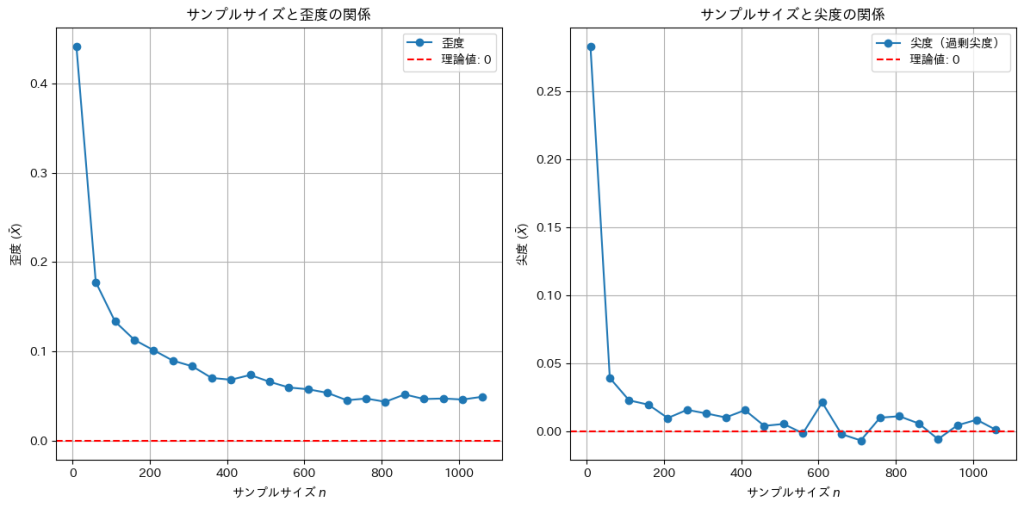
Xの標本平均の尖度(過剰尖度)はサンプルサイズnが大きくなると0に近づくことが確認できました。しかし歪度は0に近づくスピードは遅いです。Xが従うガンマ分布は元々歪度を持つ非対称な分布なので、そのようになります。サンプルサイズnを10,000まで大きくしてみます。
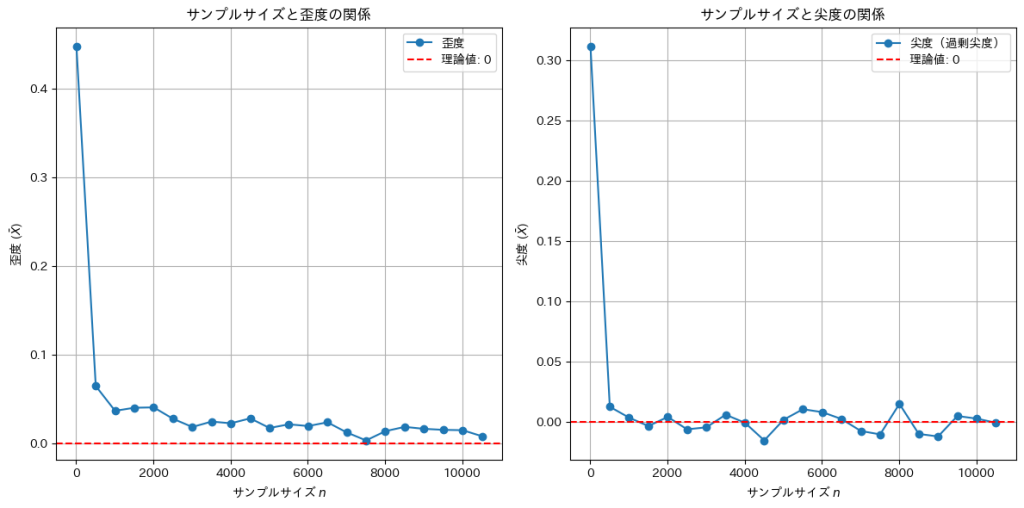
nが十分に大きくなったので歪度も0に近づきました。
次に、サンプルサイズnに伴う標本平均の分布が正規分布に近づく様子を確認します。
# 2017 Q1(4) 2024.10.27
import seaborn as sns
from scipy.stats import norm
# サンプルサイズの設定
selected_sample_sizes = [5, 20, 100, 200] # 表示するサンプルサイズの選択
num_simulations = 10000 # シミュレーションの繰り返し回数
# グラフの作成
plt.figure(figsize=(14, 10))
# 各サンプルサイズでのシミュレーションとヒストグラムの描画
for idx, n in enumerate(selected_sample_sizes):
sample_means = []
# シミュレーションの実行
for _ in range(num_simulations):
sample = population_dist.rvs(size=n) # サンプルを抽出
sample_mean = np.mean(sample) # 標本平均を計算
sample_means.append(sample_mean)
# ヒストグラムのプロット
plt.subplot(2, 2, idx + 1)
sns.histplot(sample_means, bins=30, kde=True, stat="density", color='blue', label='標本平均の分布')
# 正規分布のプロット
mean_of_means = np.mean(sample_means)
std_of_means = np.std(sample_means)
x = np.linspace(min(sample_means), max(sample_means), 100)
plt.plot(x, norm.pdf(x, mean_of_means, std_of_means), 'r--', label='正規分布')
# グラフの設定
plt.title(f'サンプルサイズ {n} の標本平均の分布')
plt.xlabel('標本平均')
plt.ylabel('密度')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()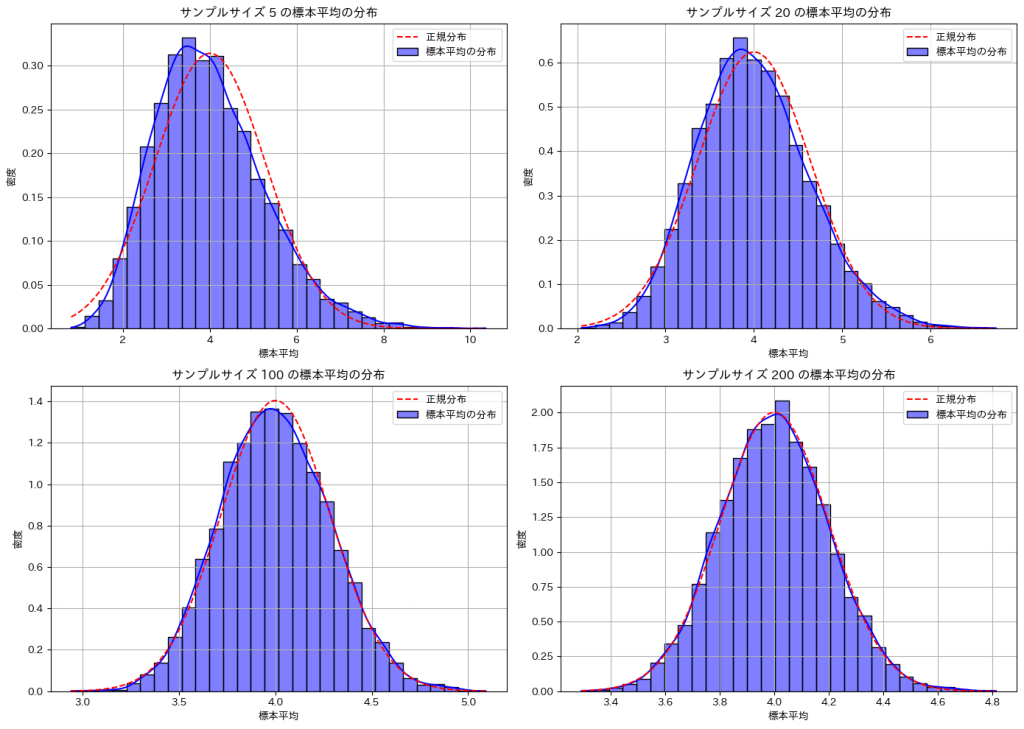
サンプルサイズnが大きくなるほど標本平均の分布は正規分布に近づくことが確認できました。
2017 Q1(3)
この前と同じ問ですが、解き方が間違っていたので、再チャレンジです。
コード
Xの標本平均の尖度(過剰尖度)が![]() になるか確認するためにシミュレーションを行います。母集団分布はガンマ分布とします。比較のためシミュレーション回数は前問(歪度)と同じ回数とする。
になるか確認するためにシミュレーションを行います。母集団分布はガンマ分布とします。比較のためシミュレーション回数は前問(歪度)と同じ回数とする。
# 2017 Q1(3) 2024.10.26
from scipy.stats import kurtosis, gamma
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータの設定
num_simulations = 30000 # シミュレーションの繰り返し回数
sample_sizes = range(10, 110, 10) # サンプルサイズの設定
# 尖度を持つ母集団分布としてガンマ分布を使用(shape=2で正の尖度を持つ)
shape_param = 2.0 # ガンマ分布のshapeパラメータ
scale_param = 2.0 # ガンマ分布のscaleパラメータ
population_dist = gamma(a=shape_param, scale=scale_param)
# 理論的な過剰尖度(ガンマ分布の尖度の計算)
beta_2_theoretical = 6 / shape_param # ガンマ分布の過剰尖度
# シミュレーション結果を保存するリスト
sample_mean_excess_kurtosis = []
# 各サンプルサイズでのシミュレーションの実行
for n in sample_sizes:
kurt_values = []
# シミュレーションを繰り返し
for _ in range(num_simulations):
sample = population_dist.rvs(size=n) # サンプルを抽出
sample_mean = np.mean(sample) # 標本平均
kurt_values.append(sample_mean)
# 標本平均の尖度を計算し、過剰尖度に変換(-3)
kurtosis_of_sample_mean = kurtosis(kurt_values, fisher=False) - 3 # 尖度を計算し、過剰尖度に変換
sample_mean_excess_kurtosis.append(kurtosis_of_sample_mean)
# 理論値の計算
theoretical_excess_kurtosis = [beta_2_theoretical / n for n in sample_sizes]
# グラフの作成
plt.figure(figsize=(10, 6))
# シミュレーション結果のプロット
plt.plot(sample_sizes, sample_mean_excess_kurtosis, marker='o', label='シミュレーション結果 (過剰尖度)')
plt.plot(sample_sizes, theoretical_excess_kurtosis, color='r', linestyle='--', label='理論値: $\\frac{\\beta_2}{n}$')
plt.title('$\\bar{X}$ の過剰尖度のシミュレーションと理論値の比較')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$\\bar{X}$ の過剰尖度')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()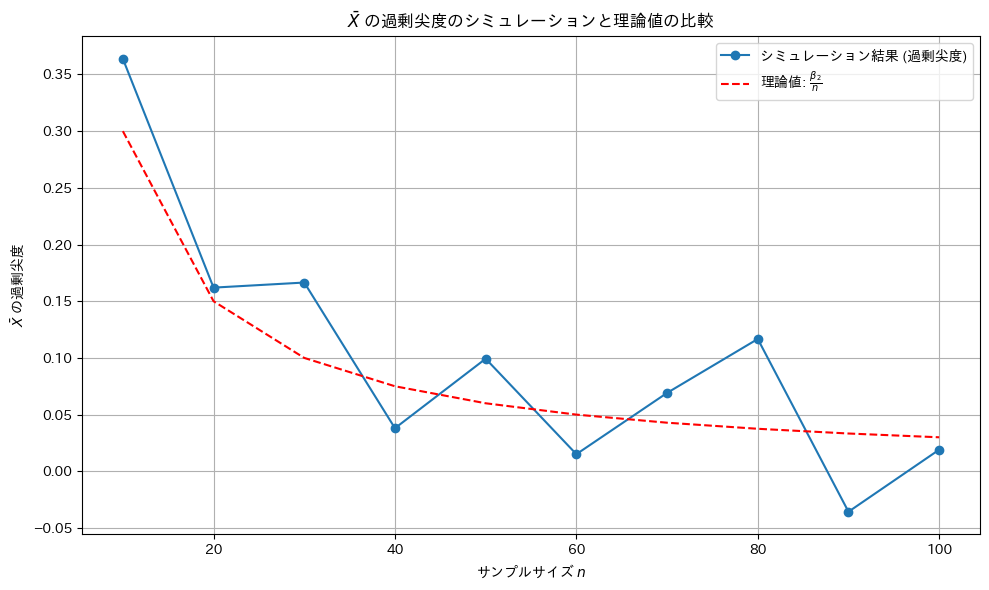
尖度は理論値に沿うものの、歪度(前問)より更に外れ値の影響を受けやすいため分散が大きい。
シミュレーション回数を10倍にしてみます。
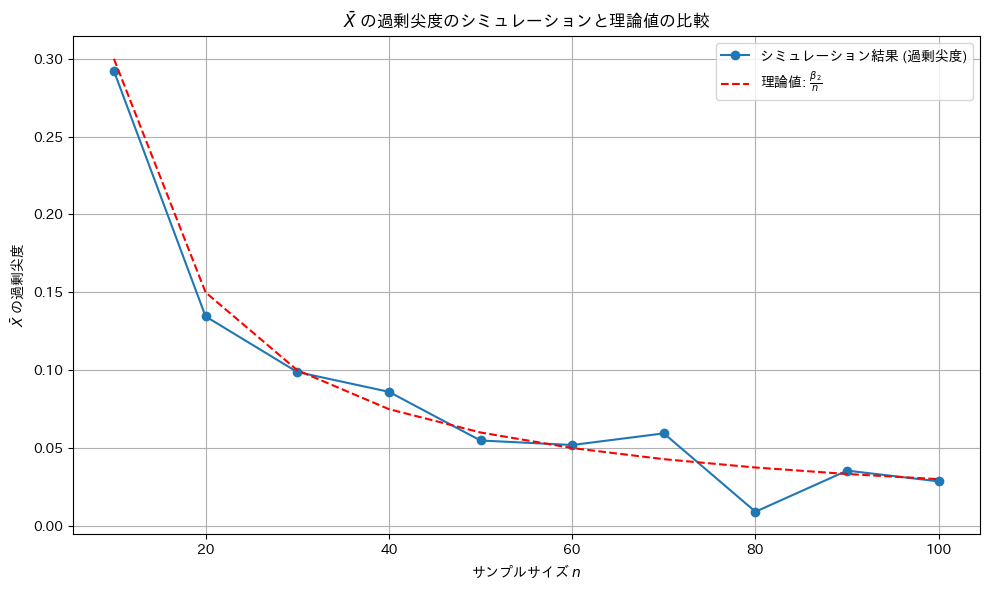
尖度は理論値に近づきました。
2017 Q1(2)
標本平均の歪度を求めました。

コード
Xの標本平均の歪度が![]() になるか確認するためにシミュレーションを行います。母集団分布はガンマ分布とします。
になるか確認するためにシミュレーションを行います。母集団分布はガンマ分布とします。
from scipy.stats import skew, gamma
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータの設定
num_simulations = 30000 # シミュレーションの繰り返し回数
sample_sizes = range(10, 110, 10) # サンプルサイズの設定
# 歪度を持つ母集団分布としてガンマ分布を使用(shape=2で正の歪度を持つ)
shape_param = 2.0 # ガンマ分布のshapeパラメータ
scale_param = 2.0 # ガンマ分布のscaleパラメータ
population_dist = gamma(a=shape_param, scale=scale_param)
# 理論的な歪度(ガンマ分布の歪度の計算)
beta_1_theoretical = 2 / np.sqrt(shape_param) # ガンマ分布の理論的な歪度
# シミュレーション結果を保存するリスト
sample_mean_skewness = []
# 各サンプルサイズでのシミュレーションの実行
for n in sample_sizes:
skew_values = []
# シミュレーションを繰り返し
for _ in range(num_simulations):
sample = population_dist.rvs(size=n) # サンプルを抽出
sample_mean = np.mean(sample) # 標本平均
skew_values.append(sample_mean)
# 標本平均の歪度を計算
skewness_of_sample_mean = skew(skew_values)
sample_mean_skewness.append(skewness_of_sample_mean)
# 理論値の計算
theoretical_skewness = [beta_1_theoretical / np.sqrt(n) for n in sample_sizes]
# グラフの作成
plt.figure(figsize=(10, 6))
# シミュレーション結果のプロット
plt.plot(sample_sizes, sample_mean_skewness, marker='o', label='シミュレーション結果')
plt.plot(sample_sizes, theoretical_skewness, color='r', linestyle='--', label='理論値: $\\frac{\\beta_1}{\sqrt{n}}$')
plt.title('$\\bar{X}$ の歪度のシミュレーションと理論値の比較')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$\\bar{X}$ の歪度')
plt.legend()
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()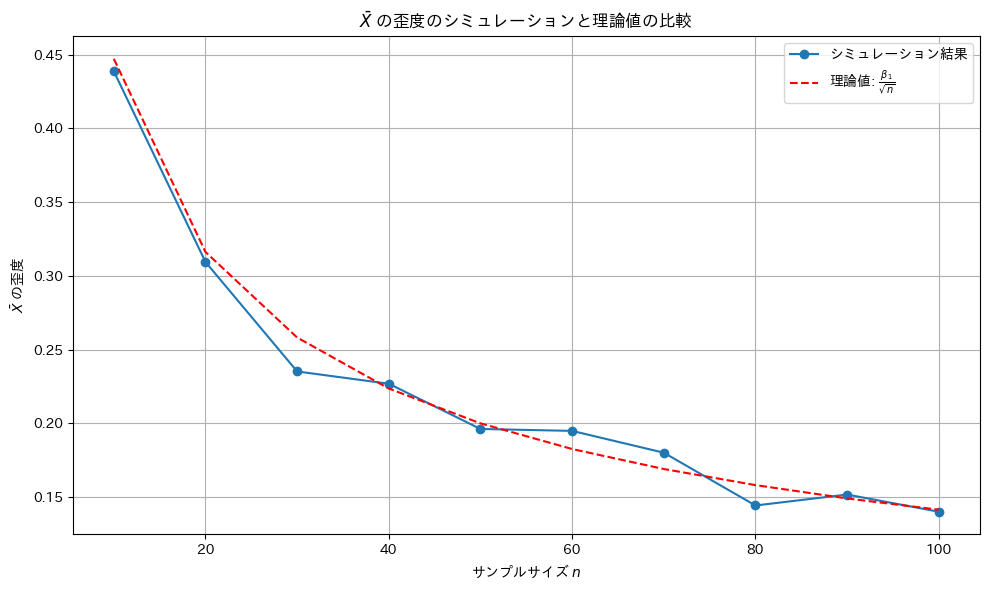
歪度は外れ値の影響を受けやすいものの概ね理論値と一致しました。
2017 Q1(1)
不偏分散が母分散の不偏推定量であることを示しました。
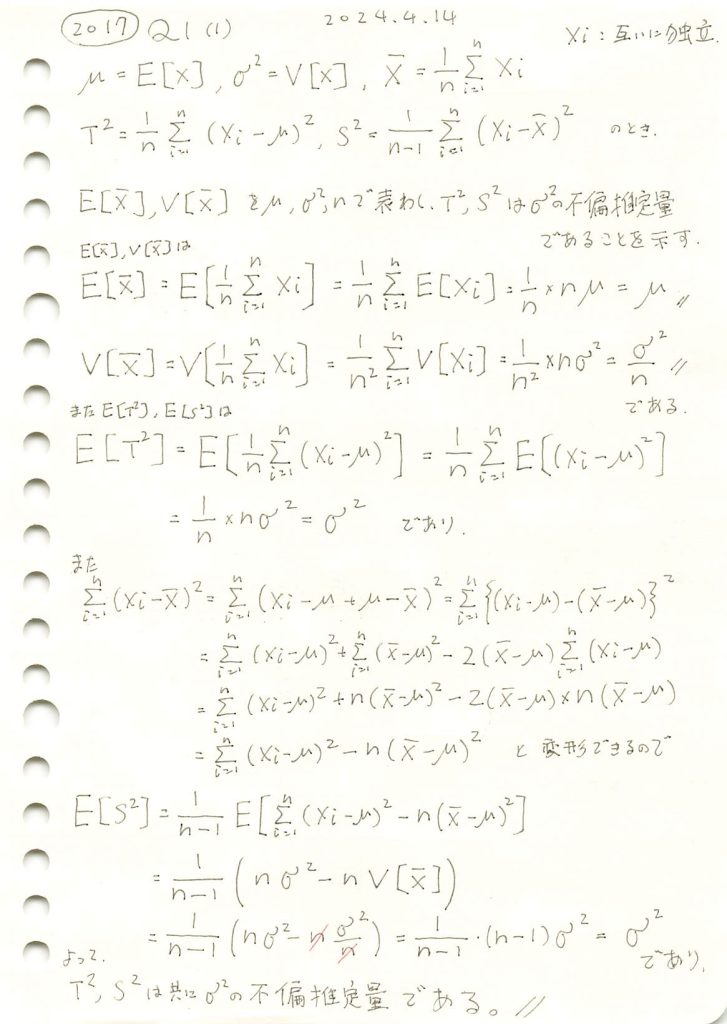
コード
サンプルサイズnを変化させて![]() ,
,![]() ,
,![]() ,
,![]() をそれぞれシミュレーションして描画します。
をそれぞれシミュレーションして描画します。
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータの設定
mu = 5.0 # 母平均
sigma = 2.0 # 母標準偏差
num_simulations = 1000 # シミュレーションの繰り返し回数
# n の範囲を設定 (100 から 10000 まで 100 刻み)
n_values = range(100, 10100, 100)
# 各 n に対する統計量を保存するリスト
E_X_bar_list = []
V_X_bar_list = []
E_T2_list = []
E_S2_list = []
# 各 n に対するシミュレーションの実行
for n in n_values:
sample_means = []
T2_values = []
S2_values = []
# シミュレーションの実行
for _ in range(num_simulations):
sample = np.random.normal(mu, sigma, n)
sample_mean = np.mean(sample)
sample_means.append(sample_mean)
# T^2 計算 (母平均使用)
T2 = np.mean((sample - mu) ** 2)
T2_values.append(T2)
# S^2 計算 (標本平均使用)
S2 = np.var(sample, ddof=1)
S2_values.append(S2)
# 結果をリストに保存
E_X_bar_list.append(np.mean(sample_means))
V_X_bar_list.append(np.var(sample_means))
E_T2_list.append(np.mean(T2_values))
E_S2_list.append(np.mean(S2_values))
# グラフの作成(理論値を追加)
plt.figure(figsize=(14, 10))
# 理論値
theoretical_mean = mu # E[X_bar] の理論値
theoretical_variance = sigma**2 / np.array(n_values) # V[X_bar] の理論値
theoretical_variance_true = sigma**2 # 母分散
# E[X_bar] のプロット
plt.subplot(2, 2, 1)
plt.plot(n_values, E_X_bar_list, marker='o', label='シミュレーション')
plt.axhline(y=theoretical_mean, color='r', linestyle='--', label='理論値: $E[\overline{X}] = \mu$')
plt.title('$E[\overline{X}]$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$E[\overline{X}]$')
plt.legend()
# V[X_bar] のプロット
plt.subplot(2, 2, 2)
plt.plot(n_values, V_X_bar_list, marker='o', label='シミュレーション')
plt.plot(n_values, theoretical_variance, color='r', linestyle='--', label='理論値: $V[\overline{X}] = \\frac{\sigma^2}{n}$')
plt.title('$V[\overline{X}]$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$V[\overline{X}]$')
plt.legend()
# E[T^2] のプロット
plt.subplot(2, 2, 3)
plt.plot(n_values, E_T2_list, marker='o', label='シミュレーション')
plt.axhline(y=theoretical_variance_true, color='r', linestyle='--', label='理論値: $E[T^2] = \sigma^2$')
plt.title('$E[T^2]$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$E[T^2]$')
plt.legend()
# E[S^2] のプロット
plt.subplot(2, 2, 4)
plt.plot(n_values, E_S2_list, marker='o', label='シミュレーション')
plt.axhline(y=theoretical_variance_true, color='r', linestyle='--', label='理論値: $E[S^2] = \sigma^2$')
plt.title('$E[S^2]$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('$E[S^2]$')
plt.legend()
# グラフの表示
plt.tight_layout()
plt.show()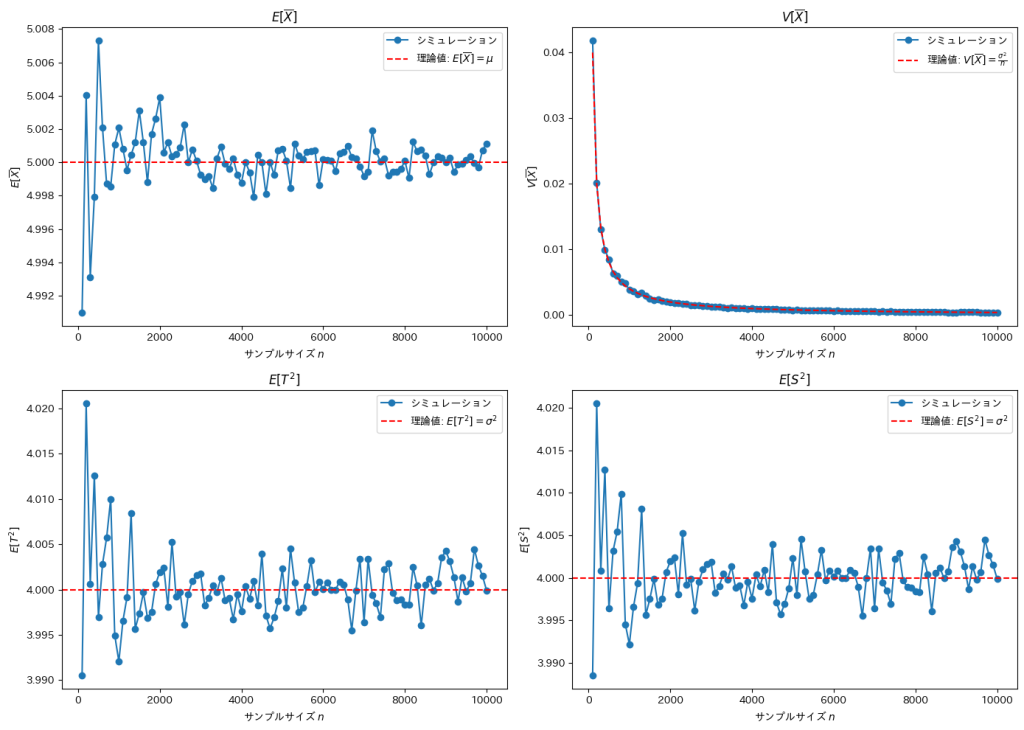
サンプルサイズnが増加するほど、各推定量は理論値に収束していく傾向に見えます。![]() と
と![]() は外れ値の影響を受けやすいため収束速度が緩やかです。
は外れ値の影響を受けやすいため収束速度が緩やかです。
2018 Q5(3)
一様分布の3つの順序統計量のうち第3と第1の確率変数の差の期待値と分散を求めました。
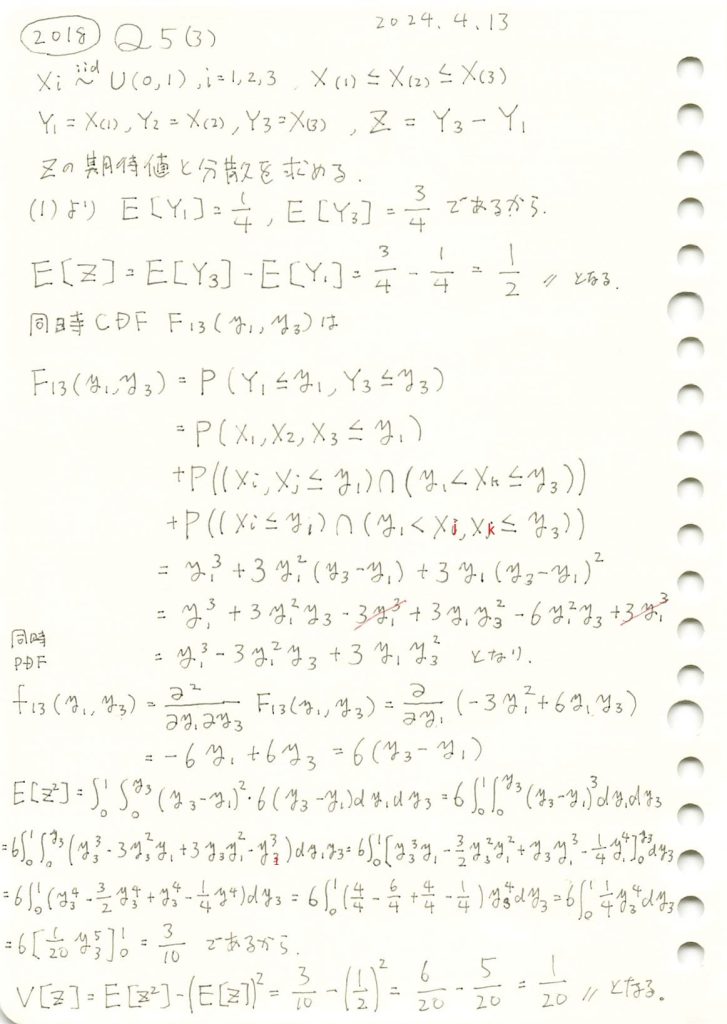
コード
同時確率密度関数f13(y1,y3)を視覚化してみます。またzが一定になる線も描画してみます。
# 2018 Q5(3) 2024.10.23
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 定義域 (y1 と y3 は [0, 1] の範囲で変動)
y1_values = np.linspace(0, 1, 100)
y3_values = np.linspace(0, 1, 100)
# メッシュグリッドを作成
Y1, Y3 = np.meshgrid(y1_values, y3_values)
# 同時確率密度関数 f13(y1, y3) = 6(y3 - y1), ただし y3 >= y1
f13 = np.where(Y3 >= Y1, 6 * (Y3 - Y1), 0)
# 等高線のための Z の値を設定 (例として Z = 0.2, 0.5, 0.8 を使用)
Z_values = [0.2, 0.5, 0.8]
# 3D グラフの描画を再度行う
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
# 3Dプロット (同時確率密度関数 f13(y1, y3))
ax.plot_surface(Y1, Y3, f13, cmap='viridis', alpha=0.8)
# 各 Z = Y3 - Y1 の線をプロット
for z_value in Z_values:
y1_line = np.linspace(0, 1 - z_value, 100)
y3_line = y1_line + z_value
ax.plot(y1_line, y3_line, zs=0, zdir='z', label=f'$Z = {z_value}$', lw=2)
# 軸ラベル
ax.set_title('同時確率密度関数 $f_{13}(y_1, y_3)$ と $Z = Y_3 - Y_1$', fontsize=14)
ax.set_xlabel('$y_1$', fontsize=12)
ax.set_ylabel('$y_3$', fontsize=12)
ax.set_zlabel('$f_{13}(y_1, y_3)$', fontsize=12)
# 凡例
ax.legend()
# グラフの表示
plt.show()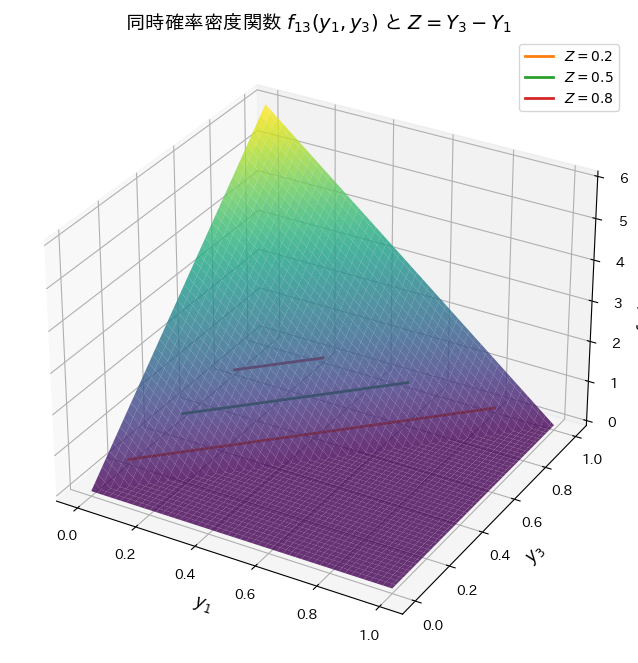
Z=z で垂直に切った断面の面積が![]() に相当します。
に相当します。
![]() を解いてZの確率密度関数を
を解いてZの確率密度関数を![]() のように求めます。順序統計量Y1とY3をシミュレーションし、理論と一致するか確認します。
のように求めます。順序統計量Y1とY3をシミュレーションし、理論と一致するか確認します。
# 2018 Q5(3) 2024.10.23
import numpy as np
import matplotlib.pyplot as plt
# サンプルデータの生成 (Z = Y3 - Y1 としてシミュレーション)
n_samples = 10000 # サンプル数
samples = np.random.uniform(0, 1, (n_samples, 3)) # 一様分布からサンプリング
Y1_samples = np.min(samples, axis=1) # 最小値 Y1
Y3_samples = np.max(samples, axis=1) # 最大値 Y3
# Z = Y3 - Y1 を計算
Z_samples = Y3_samples - Y1_samples
# Zの期待値と分散を計算
expected_Z = np.mean(Z_samples)
variance_Z = np.var(Z_samples)
# 理論値との比較
theoretical_Z_mean = 0.5
theoretical_Z_var = 1/20
# 期待値と分散を表示
print(f"シミュレーションによる E[Z](期待値): {expected_Z:.4f}, 理論値: {theoretical_Z_mean:.4f}")
print(f"シミュレーションによる Var[Z](分散): {variance_Z:.4f}, 理論値: {theoretical_Z_var:.4f}")
# Zの理論的な確率密度関数の定義
z_values = np.linspace(0, 1, 500)
f_z_theoretical = 6 * z_values * (1 - z_values)
# ヒストグラムと理論的なPDFを重ねて描画
plt.figure(figsize=(8, 6))
# サンプルのヒストグラムを描画 (確率密度として正規化)
plt.hist(Z_samples, bins=50, density=True, alpha=0.5, color='purple', label='Z samples (Y3 - Y1)')
# 理論的な確率密度関数のプロット
plt.plot(z_values, f_z_theoretical, label='Theoretical $f_Z(z) = 6z(1-z)$', color='black', linewidth=2)
# グラフの設定
plt.title('Z = Y3 - Y1 の確率密度関数 (シミュレーションと理論)', fontsize=14)
plt.xlabel('Z', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Z](期待値): 0.4992, 理論値: 0.5000
シミュレーションによる Var[Z](分散): 0.0500, 理論値: 0.0500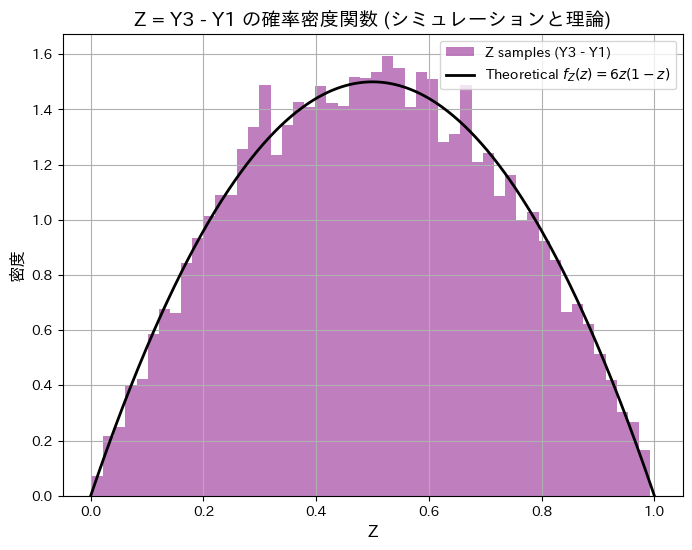
シミュレーションによる順序統計量Y3とY1の差の分布と期待値と分散が理論値と一致しました。
また興味深いことに、ZとY2は同じ分布になっていることが分かりました。
2018 Q5(2)
一様分布の3つの順序統計量のうち真ん中の確率密度関数と確率の計算をしました。
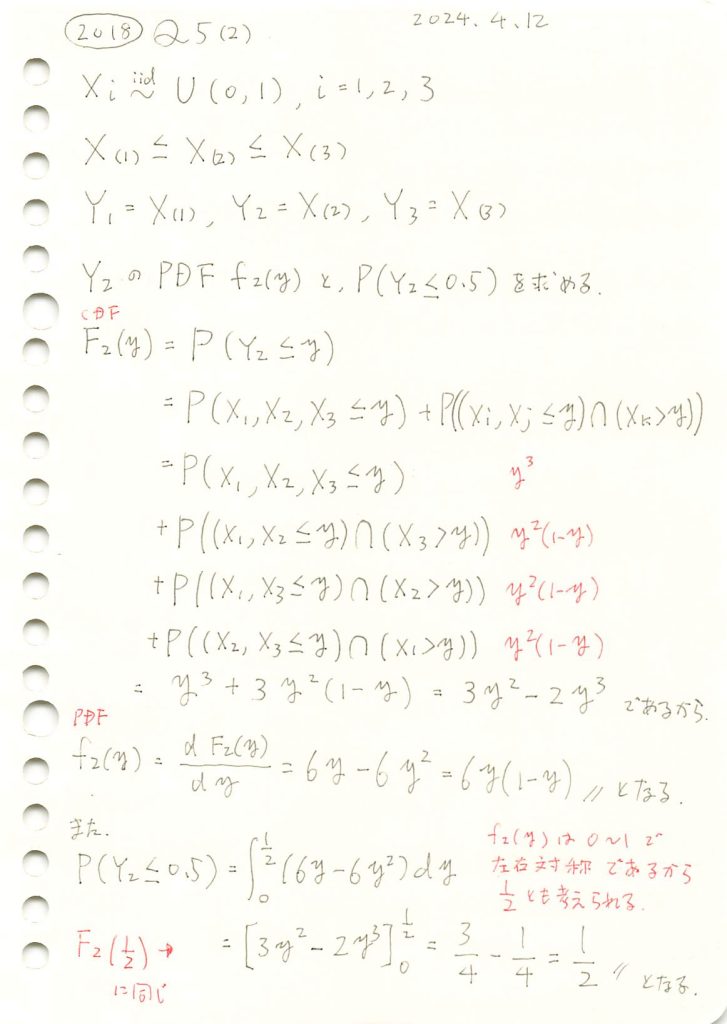
コード
シミュレーションにより順序統計量Y2の分布と期待値が理論値と一致するか確認します。
# 2018 Q5(2) 2024.10.22
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数 f2(y) の定義
f2_y = 6 * y_values * (1 - y_values)
# シミュレーションの設定
n_samples = 10000 # サンプル数
# 一様分布から3つの変数をサンプリング
samples = np.random.uniform(0, 1, (n_samples, 3))
# 順序統計量の第2要素を抽出 (Y2)
Y2_samples = np.median(samples, axis=1) # 中央値
# 期待値の計算
expected_Y2 = np.mean(Y2_samples)
# 理論値との比較
theoretical_Y2 = 0.5 # 中央値
# 期待値を表示
print(f"シミュレーションによる E[Y2](中間値の期待値): {expected_Y2:.4f}, 理論値: {theoretical_Y2:.4f}")
# ヒストグラムの作成
plt.figure(figsize=(8, 6))
# 理論密度関数 f2(y) のプロット
plt.plot(y_values, f2_y, label='$f_2(y) = 6y(1-y)$', color='red')
# サンプルのヒストグラムを追加 (確率密度として正規化)
plt.hist(Y2_samples, bins=50, density=True, alpha=0.5, color='red', label='Y2 samples (median)')
# グラフの設定
plt.title('確率密度関数 $f_2(y)$ とヒストグラム (シミュレーションと理論)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Y2](中間値の期待値): 0.5006, 理論値: 0.5000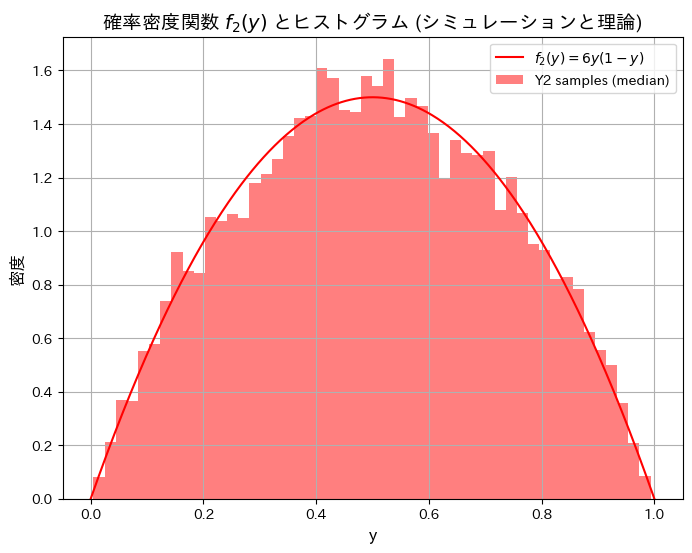
シミュレーションによる順序統計量Y1とY3の分布と期待値が理論値と一致しました。
次に、Y1~Y3の確率密度関数と累積分布関数を重ねて見てみます。
# 2018 Q5(2) 2024.10.22
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数の定義
f1_y = 3 * (1 - y_values) ** 2
f2_y = 6 * y_values * (1 - y_values)
f3_y = 3 * y_values ** 2
# CDF (累積分布関数) の計算
cdf1_y = np.cumsum(f1_y) * (y_values[1] - y_values[0])
cdf2_y = np.cumsum(f2_y) * (y_values[1] - y_values[0])
cdf3_y = np.cumsum(f3_y) * (y_values[1] - y_values[0])
# グラフの作成
plt.figure(figsize=(10, 8))
# 確率密度関数 (PDF) のプロット
plt.subplot(2, 1, 1)
plt.plot(y_values, f1_y, label='$f_1(y)$', color='blue')
plt.plot(y_values, f2_y, label='$f_2(y)$', color='red')
plt.plot(y_values, f3_y, label='$f_3(y)$', color='green')
plt.title('確率密度関数 (PDF)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# 累積分布関数 (CDF) のプロット
plt.subplot(2, 1, 2)
plt.plot(y_values, cdf1_y, label='$F_1(y)$', color='blue')
plt.plot(y_values, cdf2_y, label='$F_2(y)$', color='red')
plt.plot(y_values, cdf3_y, label='$F_3(y)$', color='green')
plt.title('累積分布関数 (CDF)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('累積確率', fontsize=12)
plt.legend(loc='lower right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.tight_layout()
plt.show()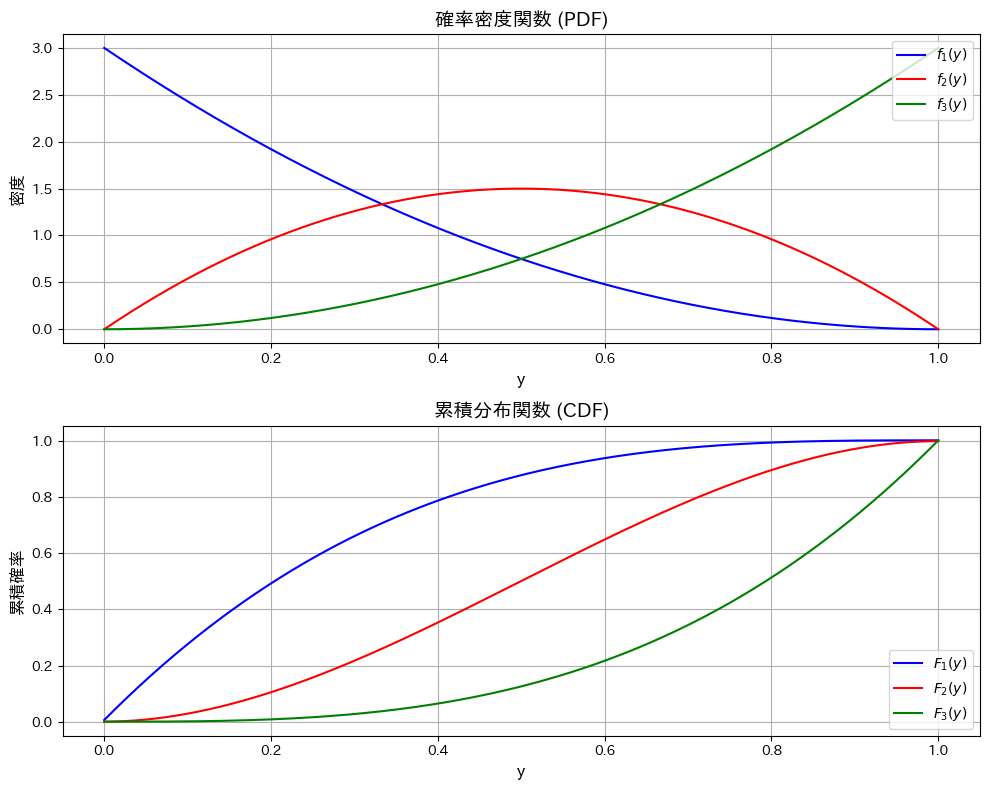
Y1は左寄り、Y2は中央寄り、Y3は右寄りになっていて、順序統計量の性質を直感的に表されています。Y2の確率密度関数は左右対称なので期待値が0.5になることも分かります。Y2の累積分布関数が直線でないことも面白いです。
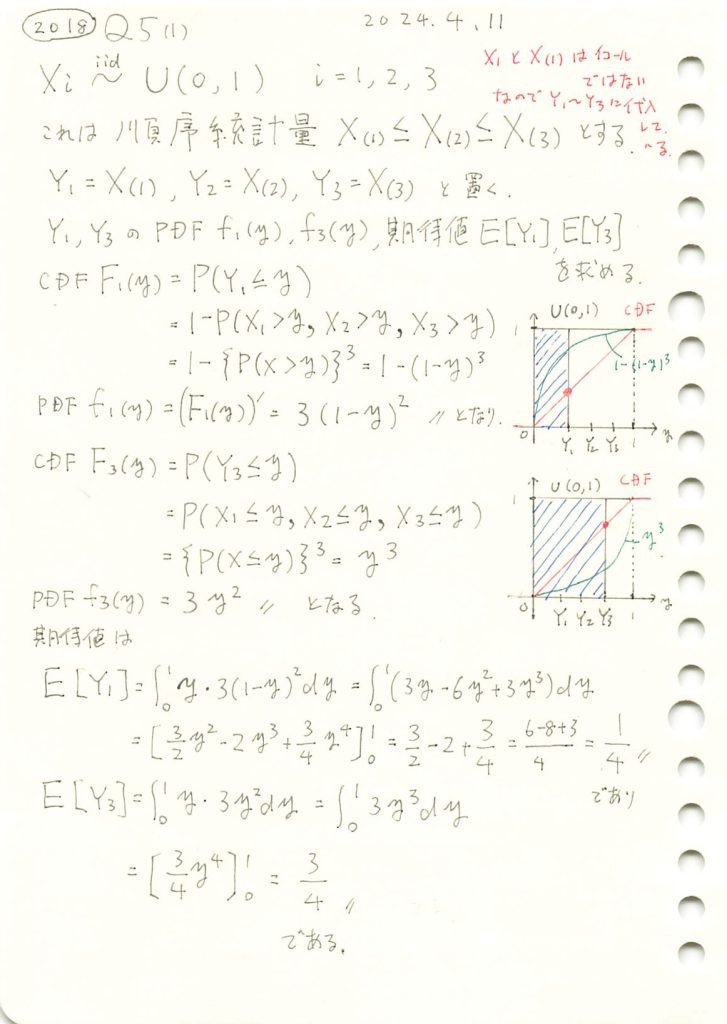
2018 Q5(1)
一様分布の順序統計量の確率密度関数と期待値を求めました。
コード
シミュレーションにより順序統計量Y1とY3の分布と期待値が理論値と一致するか確認します。
# 2018 Q5(1) 2024.10.21
import numpy as np
import matplotlib.pyplot as plt
# 定義域
y_values = np.linspace(0, 1, 500)
# 確率密度関数の定義
f1_y = 3 * (1 - y_values) ** 2
f3_y = 3 * y_values ** 2
# シミュレーションの設定
n_samples = 10000 # サンプル数
# 一様分布から3つの変数をサンプリング
samples = np.random.uniform(0, 1, (n_samples, 3))
# 順序統計量を求める
Y1_samples = np.min(samples, axis=1) # 最小値
Y3_samples = np.max(samples, axis=1) # 最大値
# 期待値の計算
expected_Y1 = np.mean(Y1_samples)
expected_Y3 = np.mean(Y3_samples)
# 理論値との比較
theoretical_Y1 = 1/4
theoretical_Y3 = 3/4
# 期待値を表示
print(f"シミュレーションによる E[Y1](最小値の期待値): {expected_Y1:.4f}, 理論値: {theoretical_Y1:.4f}")
print(f"シミュレーションによる E[Y3](最大値の期待値): {expected_Y3:.4f}, 理論値: {theoretical_Y3:.4f}")
# ヒストグラムの作成
plt.figure(figsize=(8, 6))
# 理論密度関数のプロット
plt.plot(y_values, f1_y, label='$f_1(y) = 3(1-y)^2$', color='blue')
plt.plot(y_values, f3_y, label='$f_3(y) = 3y^2$', color='green')
# サンプルのヒストグラムを追加 (確率密度として正規化)
plt.hist(Y1_samples, bins=50, density=True, alpha=0.5, color='blue', label='Y1 samples (min)')
plt.hist(Y3_samples, bins=50, density=True, alpha=0.5, color='green', label='Y3 samples (max)')
# グラフの設定
plt.title('確率密度関数 $f_1(y)$ と $f_3(y)$ (シミュレーションと理論)', fontsize=14)
plt.xlabel('y', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend(loc='upper right', fontsize=10)
plt.grid(True)
# グラフの表示
plt.show()シミュレーションによる E[Y1](最小値の期待値): 0.2499, 理論値: 0.2500
シミュレーションによる E[Y3](最大値の期待値): 0.7487, 理論値: 0.7500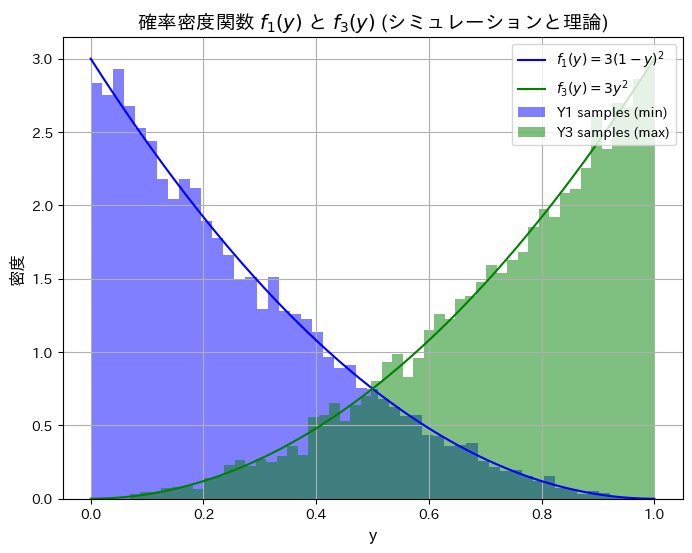
シミュレーションによる順序統計量Y1とY3の分布と期待値が理論値と一致しました。