ホーム » コードあり (ページ 6)
「コードあり」カテゴリーアーカイブ
2016 Q5(2)
2水準の一元分散分析で総変動と群間変動の分散比が、群間変動と郡内変動の分散比を使って表せることを確かめました。

コード
二つの![]() が等価であるかシミュレーションによって検証してみます。
が等価であるかシミュレーションによって検証してみます。
# 2016 Q5(2) 2024.11.28
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ設定
n = 100 # 全体のサンプル数
repeats = 10000 # シミュレーションの繰り返し回数
# シミュレーション結果を格納するリスト
d2_direct_simulations = []
d2_simplified_simulations = []
# シミュレーションを実行
np.random.seed(42) # 再現性のため乱数の種を固定
for _ in range(repeats):
# 群間平方和 (SSB), 群内平方和 (SSW) を正の値でランダム生成
SSB = np.random.uniform(0.1, 10)
SSW = np.random.uniform(0.1, 10)
# SST = SSB + SSW の関係を利用
SST = SSB + SSW
# F値を計算
F = SSB / (SSW / (n - 2))
# d^2 の直接計算
d2_direct = SSB / (SST / (n - 1))
d2_direct_simulations.append(d2_direct)
# d^2 の簡略化された式による計算
d2_simplified = (n - 1) * F / (n - 2 + F)
d2_simplified_simulations.append(d2_simplified)
# 平均絶対差を計算
mean_absolute_difference = np.mean(np.abs(np.array(d2_direct_simulations) - np.array(d2_simplified_simulations)))
# 結果を出力
print(f"シミュレーションによる d^2 の平均絶対差: {mean_absolute_difference:.2e}")
# 数式を含む散布図をプロット
plt.figure(figsize=(8, 6))
plt.scatter(d2_direct_simulations, d2_simplified_simulations, alpha=0.5, s=10, label="シミュレーション結果")
plt.plot([min(d2_direct_simulations), max(d2_direct_simulations)],
[min(d2_direct_simulations), max(d2_direct_simulations)], 'r--', label="$y=x$") # y=xの基準線
plt.title("$d^2$ の二式の比較", fontsize=14)
plt.xlabel(r"$d^2 = \frac{\mathrm{SSB}}{\mathrm{SST} / (n-1)}$", fontsize=12)
plt.ylabel(r"$d^2 = \frac{(n-1)F}{n-2+F}$", fontsize=12)
plt.legend(fontsize=12) # 凡例を追加
plt.grid(alpha=0.3) # グリッドを薄く表示
plt.show()シミュレーションによる d^2 の平均絶対差: 3.97e-15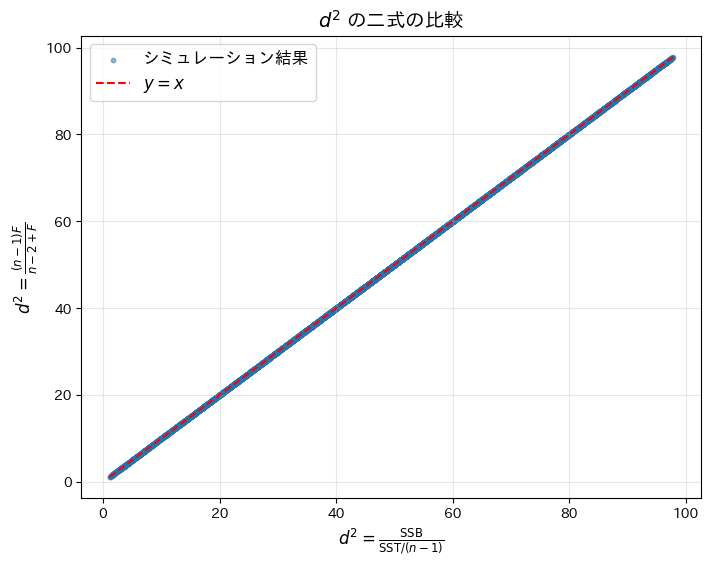
二つの![]() が等価であることがシミュレーションによって確認されました。なお、平均絶対差が僅かに生じたのは、浮動小数点演算による誤差であると考えられます。
が等価であることがシミュレーションによって確認されました。なお、平均絶対差が僅かに生じたのは、浮動小数点演算による誤差であると考えられます。
2016 Q5(1)
MCAR性の検定統計量が与式になることを示しました。
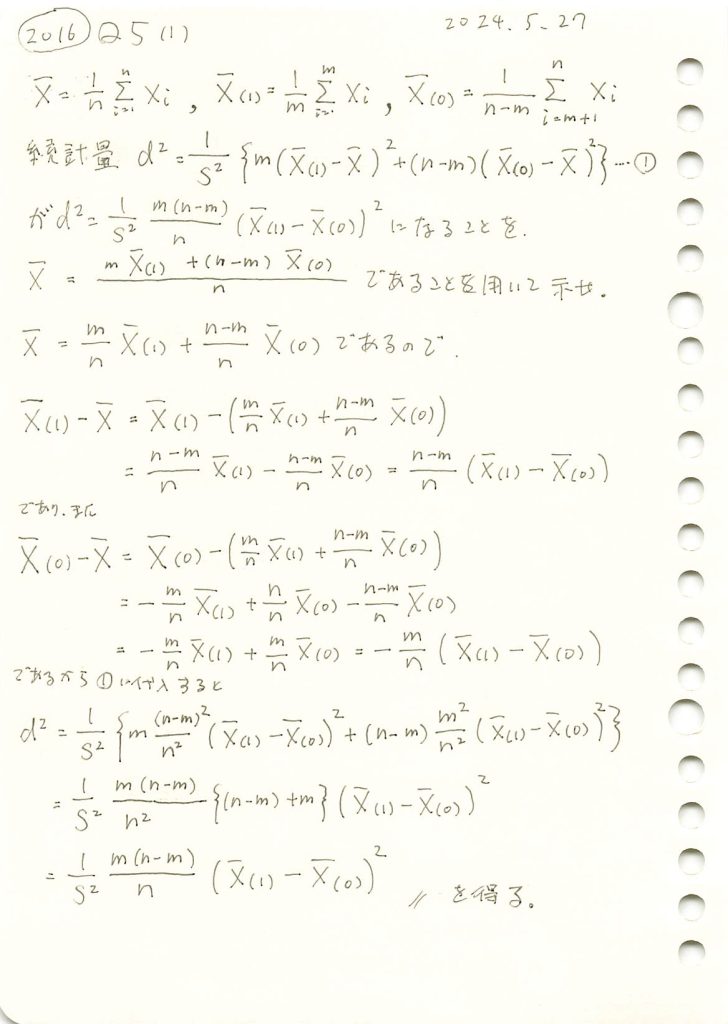
コード
二つの![]() が等価であるかシミュレーションによって検証してみます。
が等価であるかシミュレーションによって検証してみます。
# 2016 Q5(1) 2024.11.27
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 100 # 全体のサンプル数
m = 60 # 観測可能なデータのペア数
repeats = 10000 # シミュレーションの繰り返し回数
# Xのデータを正規分布に従ってランダムに生成
np.random.seed(42) # 乱数の再現性を確保
X = np.random.normal(loc=0, scale=1, size=n)
# データの欠損をシミュレート
X1 = X[:m] # 観測可能なXの値
X0 = X[m:] # Yが欠損しているXの値
# 理論的なd^2値を計算
S2 = np.var(X, ddof=1) # Xの標本不偏分散
X1_bar = np.mean(X1) # 観測可能なXの標本平均
X0_bar = np.mean(X0) # 欠損部分のXの標本平均
X_bar = np.mean(X) # 全体のXの標本平均
# d^2の直接計算
d2_direct = (1 / S2) * (m * (X1_bar - X_bar)**2 + (n - m) * (X0_bar - X_bar)**2)
# d^2の簡略化された計算
d2_simplified = (1 / S2) * (m * (n - m) / n) * (X1_bar - X0_bar)**2
# シミュレーションを実行して比較
d2_direct_simulations = []
d2_simplified_simulations = []
for _ in range(repeats):
# Xを再生成してランダムサンプリングをシミュレート
X = np.random.normal(loc=0, scale=1, size=n)
X1 = X[:m]
X0 = X[m:]
# 各種統計量を再計算
S2 = np.var(X, ddof=1)
X1_bar = np.mean(X1)
X0_bar = np.mean(X0)
X_bar = np.mean(X)
# d^2値を計算してリストに格納
d2_direct_simulations.append((1 / S2) * (m * (X1_bar - X_bar)**2 + (n - m) * (X0_bar - X_bar)**2))
d2_simplified_simulations.append((1 / S2) * (m * (n - m) / n) * (X1_bar - X0_bar)**2)
# 平均絶対差を計算
mean_absolute_difference = np.mean(np.abs(np.array(d2_direct_simulations) - np.array(d2_simplified_simulations)))
# 計算結果を出力
print(f"シミュレーションによるd^2 の平均絶対差: {mean_absolute_difference:.2e}")
# 数式を含む散布図をプロット
plt.figure(figsize=(8, 6))
plt.scatter(d2_direct_simulations, d2_simplified_simulations, alpha=0.5, s=10, label="シミュレーション結果")
plt.plot([min(d2_direct_simulations), max(d2_direct_simulations)],
[min(d2_direct_simulations), max(d2_direct_simulations)], 'r--', label="$y=x$") # y=xの基準線
plt.title("$d^2$ の二式の比較", fontsize=14)
plt.xlabel(r"$d^2 = \frac{1}{S^2} \left[ m(\overline{X}_{(1)} - \overline{X})^2 + (n-m)(\overline{X}_{(0)} - \overline{X})^2 \right]$", fontsize=12)
plt.ylabel(r"$d^2 = \frac{1}{S^2} \cdot \frac{m(n-m)}{n} \cdot (\overline{X}_{(1)} - \overline{X}_{(0)})^2$", fontsize=12)
plt.legend(fontsize=12) # 凡例を追加
plt.grid(alpha=0.3) # グリッドを薄く表示
plt.show()シミュレーションによるd^2 の平均絶対差: 1.26e-16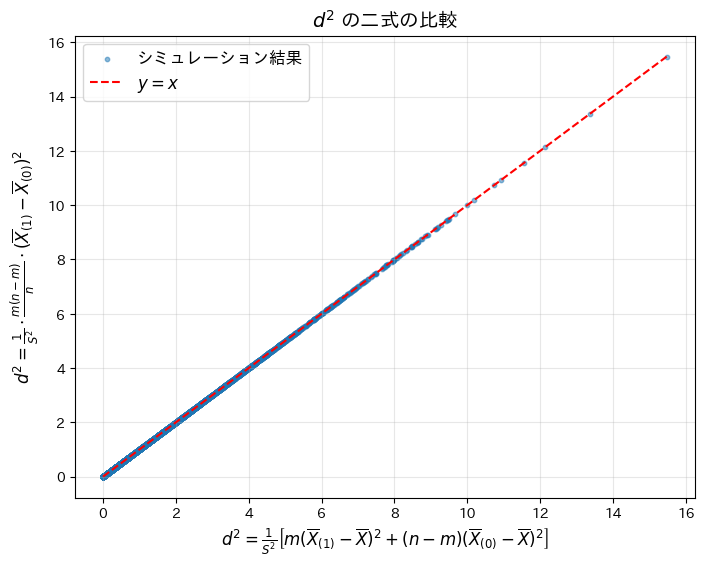
二つの![]() が等価であることがシミュレーションによって確認されました。なお、平均絶対差が僅かに生じたのは、浮動小数点演算による誤差であると考えられます。
が等価であることがシミュレーションによって確認されました。なお、平均絶対差が僅かに生じたのは、浮動小数点演算による誤差であると考えられます。
2016 Q4(4)
標準正規分布に従う乱数が0以上1以下となる確率の3つ推定量の分散が同じになるためのサンプル数を求めました。
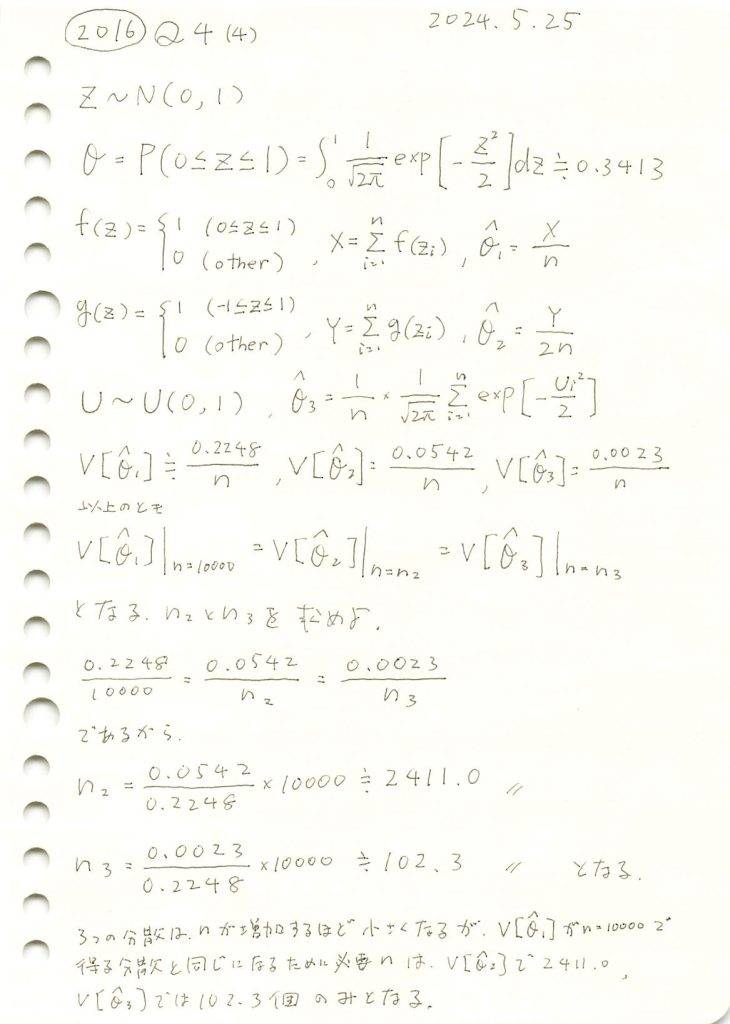
コード
θの三つの推定量![]() ,
,![]() ,
,![]() の分布と分散を視覚化し比較します。まずn1=n2=n3=10000としてシミュレーションを行います。
の分布と分散を視覚化し比較します。まずn1=n2=n3=10000としてシミュレーションを行います。
# 2016 Q4(4) 2024.11.26
# n を同じ値に設定して三つの推定量を比較する
# 必要なライブラリをインポート
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n_common = 10000 # n を全ての推定量で共通に設定
n_trials = 1000 # シミュレーション試行回数
# 推定量のリストを作成
theta_hat_1_values = []
theta_hat_2_values = []
theta_hat_3_values = []
# シミュレーション実行
for _ in range(n_trials):
# 推定量 θ̂1
samples_1 = np.random.normal(0, 1, n_common)
X = np.sum((samples_1 >= 0) & (samples_1 <= 1))
theta_hat_1_values.append(X / n_common)
# 推定量 θ̂2
samples_2 = np.random.normal(0, 1, n_common)
Y = np.sum(np.abs(samples_2) <= 1)
theta_hat_2_values.append(Y / (2 * n_common))
# 推定量 θ̂3
U = np.random.uniform(0, 1, n_common)
theta_hat_3 = np.mean((1 / np.sqrt(2 * np.pi)) * np.exp(-U**2 / 2))
theta_hat_3_values.append(theta_hat_3)
# 各推定量の分散を計算
var_theta_hat_1 = np.var(theta_hat_1_values)
var_theta_hat_2 = np.var(theta_hat_2_values)
var_theta_hat_3 = np.var(theta_hat_3_values)
# グラフ描画
fig = plt.figure(figsize=(12, 8)) # 全体の図を作成
gs = fig.add_gridspec(3, 2, width_ratios=[3, 1]) # ヒストグラムとバーグラフの比率を指定
# 共通の横軸レンジ
x_min, x_max = 0.325, 0.355
# ヒストグラム: θ̂1
ax1 = fig.add_subplot(gs[0, 0])
ax1.hist(theta_hat_1_values, bins=20, density=True, color='blue', alpha=0.7, label='$\\hat{\\theta}_1$')
ax1.axvline(theta, color='red', linestyle='--', label='理論値 $\\theta$')
ax1.set_xlim(x_min, x_max)
ax1.set_title('$\\hat{\\theta}_1$ の分布 (n = 1,000)', fontsize=12)
ax1.set_ylabel('確率密度', fontsize=10)
ax1.legend(fontsize=10)
ax1.grid(alpha=0.3)
# ヒストグラム: θ̂2
ax2 = fig.add_subplot(gs[1, 0])
ax2.hist(theta_hat_2_values, bins=20, density=True, color='green', alpha=0.7, label='$\\hat{\\theta}_2$')
ax2.axvline(theta, color='red', linestyle='--', label='理論値 $\\theta$')
ax2.set_xlim(x_min, x_max)
ax2.set_title('$\\hat{\\theta}_2$ の分布 (n = 1,000)', fontsize=12)
ax2.set_ylabel('確率密度', fontsize=10)
ax2.legend(fontsize=10)
ax2.grid(alpha=0.3)
# ヒストグラム: θ̂3
ax3 = fig.add_subplot(gs[2, 0])
ax3.hist(theta_hat_3_values, bins=20, density=True, color='orange', alpha=0.7, label='$\\hat{\\theta}_3$')
ax3.axvline(theta, color='red', linestyle='--', label='理論値 $\\theta$')
ax3.set_xlim(x_min, x_max)
ax3.set_title('$\\hat{\\theta}_3$ の分布 (n = 1,000)', fontsize=12)
ax3.set_xlabel('推定値', fontsize=10)
ax3.set_ylabel('確率密度', fontsize=10)
ax3.legend(fontsize=10)
ax3.grid(alpha=0.3)
# バーグラフ
ax_bar = fig.add_subplot(gs[:, 1]) # 全行を使う
labels = ['$\\hat{\\theta}_1$', '$\\hat{\\theta}_2$', '$\\hat{\\theta}_3$']
variances = [var_theta_hat_1, var_theta_hat_2, var_theta_hat_3]
colors = ['blue', 'green', 'orange']
ax_bar.bar(labels, variances, color=colors, alpha=0.7)
ax_bar.set_title('各推定量の分散 (n = 1,000)', fontsize=12)
ax_bar.set_ylabel('分散', fontsize=10)
ax_bar.grid(axis='y', alpha=0.3)
# 全体の調整
plt.tight_layout()
plt.show()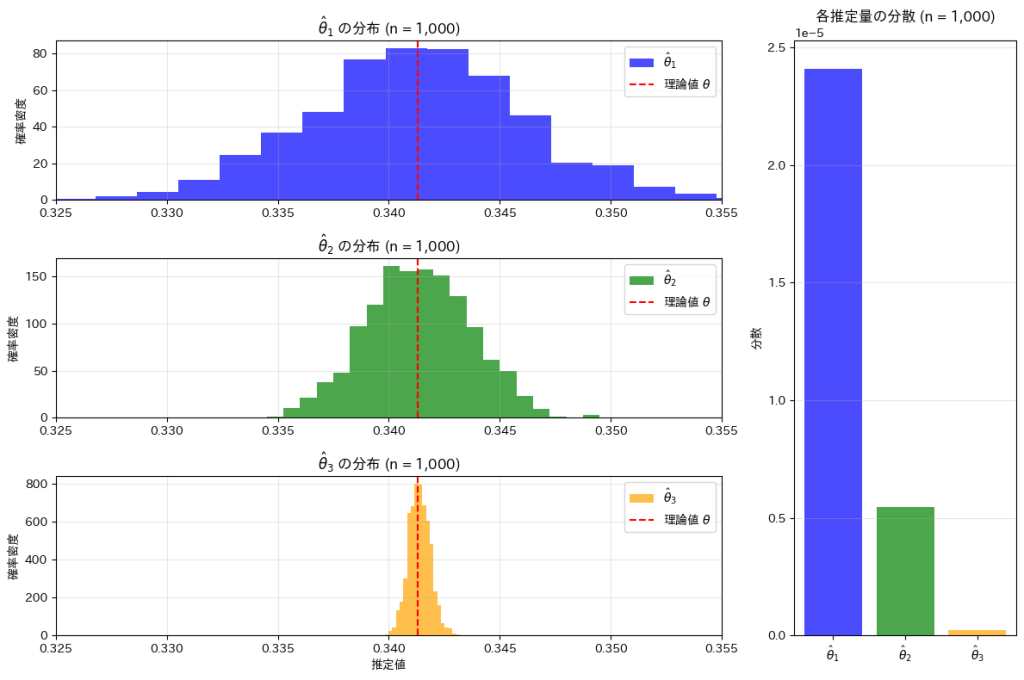
![]() <
<![]() <
<![]() の順にバラつきが小さくなり、分散も同様に小さくなっていることが確認できました。
の順にバラつきが小さくなり、分散も同様に小さくなっていることが確認できました。
次に、n1=10000, n2=2411, n3 = 102に設定してシミュレーションを行います。
# 2016 Q4(4) 2024.11.26
# 必要なライブラリをインポート
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n1, n2, n3 = 10000, 2411, 102 # 各推定量のサンプルサイズ
theta = 0.3413 # 理論値
n_trials = 1000 # シミュレーション試行回数
# 推定量のリストを作成
theta_hat_1_values = []
theta_hat_2_values = []
theta_hat_3_values = []
# シミュレーション実行
for _ in range(n_trials):
# 推定量 θ̂1
samples_1 = np.random.normal(0, 1, n1)
X = np.sum((samples_1 >= 0) & (samples_1 <= 1))
theta_hat_1_values.append(X / n1)
# 推定量 θ̂2
samples_2 = np.random.normal(0, 1, n2)
Y = np.sum(np.abs(samples_2) <= 1)
theta_hat_2_values.append(Y / (2 * n2))
# 推定量 θ̂3
U = np.random.uniform(0, 1, n3)
theta_hat_3 = np.mean((1 / np.sqrt(2 * np.pi)) * np.exp(-U**2 / 2))
theta_hat_3_values.append(theta_hat_3)
# 各推定量の分散を計算
var_theta_hat_1 = np.var(theta_hat_1_values)
var_theta_hat_2 = np.var(theta_hat_2_values)
var_theta_hat_3 = np.var(theta_hat_3_values)
# グラフ描画
fig = plt.figure(figsize=(12, 8)) # 全体の図を作成
gs = fig.add_gridspec(3, 2, width_ratios=[3, 1]) # ヒストグラムとバーグラフの比率を指定
# 共通の横軸レンジ
x_min, x_max = 0.325, 0.355
# ヒストグラム: θ̂1
ax1 = fig.add_subplot(gs[0, 0])
ax1.hist(theta_hat_1_values, bins=20, density=True, color='blue', alpha=0.7, label='$\\hat{\\theta}_1$')
ax1.axvline(theta, color='red', linestyle='--', label='理論値 $\\theta$')
ax1.set_xlim(x_min, x_max)
ax1.set_title('$\\hat{\\theta}_1$ の分布 (n = 10,000)', fontsize=12)
ax1.set_ylabel('確率密度', fontsize=10)
ax1.legend(fontsize=10)
ax1.grid(alpha=0.3)
# ヒストグラム: θ̂2
ax2 = fig.add_subplot(gs[1, 0])
ax2.hist(theta_hat_2_values, bins=20, density=True, color='green', alpha=0.7, label='$\\hat{\\theta}_2$')
ax2.axvline(theta, color='red', linestyle='--', label='理論値 $\\theta$')
ax2.set_xlim(x_min, x_max)
ax2.set_title('$\\hat{\\theta}_2$ の分布 (n = 2,411)', fontsize=12)
ax2.set_ylabel('確率密度', fontsize=10)
ax2.legend(fontsize=10)
ax2.grid(alpha=0.3)
# ヒストグラム: θ̂3
ax3 = fig.add_subplot(gs[2, 0])
ax3.hist(theta_hat_3_values, bins=20, density=True, color='orange', alpha=0.7, label='$\\hat{\\theta}_3$')
ax3.axvline(theta, color='red', linestyle='--', label='理論値 $\\theta$')
ax3.set_xlim(x_min, x_max)
ax3.set_title('$\\hat{\\theta}_3$ の分布 (n = 102)', fontsize=12)
ax3.set_xlabel('推定値', fontsize=10)
ax3.set_ylabel('確率密度', fontsize=10)
ax3.legend(fontsize=10)
ax3.grid(alpha=0.3)
# バーグラフ
ax_bar = fig.add_subplot(gs[:, 1]) # 全行を使う
labels = ['$\\hat{\\theta}_1$', '$\\hat{\\theta}_2$', '$\\hat{\\theta}_3$']
variances = [var_theta_hat_1, var_theta_hat_2, var_theta_hat_3]
colors = ['blue', 'green', 'orange']
ax_bar.bar(labels, variances, color=colors, alpha=0.7)
ax_bar.set_title('各推定量の分散', fontsize=12)
ax_bar.set_ylabel('分散', fontsize=10)
ax_bar.grid(axis='y', alpha=0.3)
# 全体の調整
plt.tight_layout()
plt.show()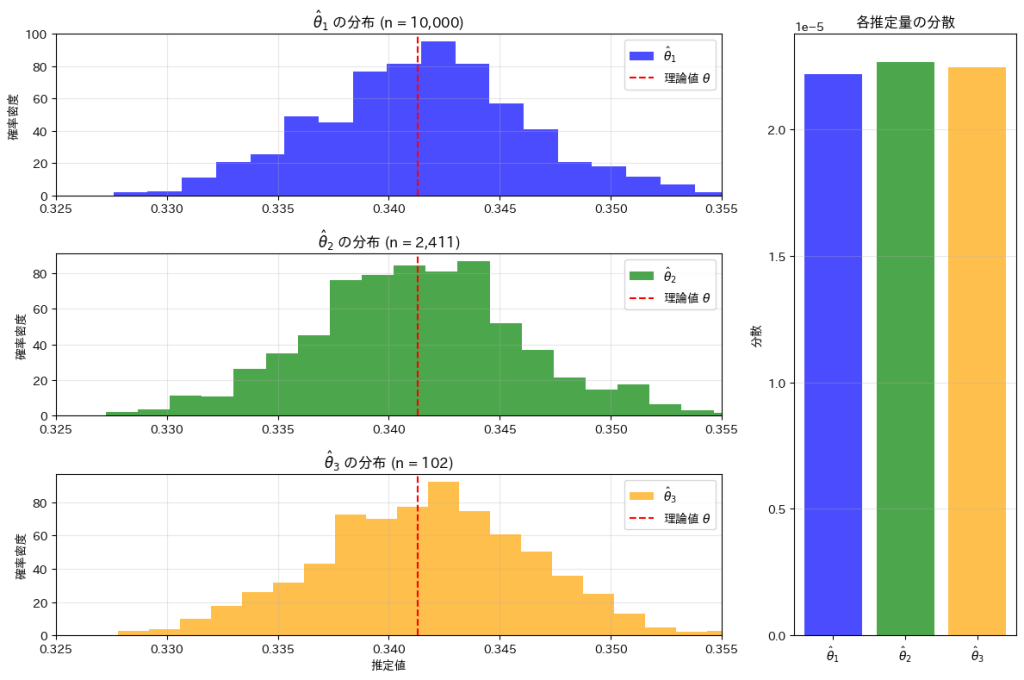
n1=10000, n2=2411, n3 = 102に設定することで、![]() ,
,![]() ,
,![]() のバラつきと分散がそれぞれほぼ等しくなっていることが確認できました。
のバラつきと分散がそれぞれほぼ等しくなっていることが確認できました。
2016 Q4(3)
一様分布に従う確率変数を標準正規分布の確率密度関数に与え、その標本平均の分散を求めました。
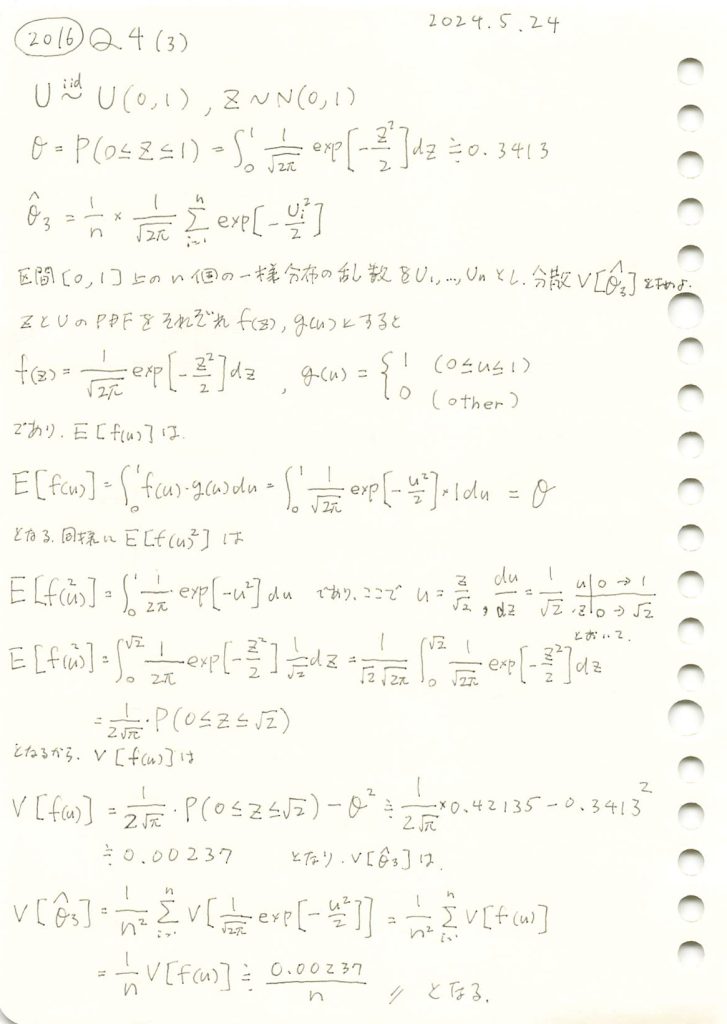
コード
θの三つの推定量![]() ,
,![]() ,
,![]() についてシミュレーションを行い、それぞれの分布を確認します。(
についてシミュレーションを行い、それぞれの分布を確認します。(![]() ,
,![]() については前問参照https://statistics.blue/2016-q41/,https://statistics.blue/2016-q42/)
については前問参照https://statistics.blue/2016-q41/,https://statistics.blue/2016-q42/)
# 2016 Q4(3) 2024.11.25
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# パラメータの設定
n = 100 # サンプルサイズ
n_trials = 1000 # シミュレーション試行回数
theta = 0.3413 # 真の成功確率
# 推定量 1: θ̂1 = X / n
theta_hat_1_values = []
for _ in range(n_trials):
samples = np.random.normal(0, 1, n)
X = np.sum((samples >= 0) & (samples <= 1)) # 0 <= Z <= 1 のカウント
theta_hat_1_values.append(X / n)
# 推定量 2: θ̂2 = Y / (2n)
theta_hat_2_values = []
for _ in range(n_trials):
samples = np.random.normal(0, 1, n)
Y = np.sum(np.abs(samples) <= 1) # |Z| <= 1 のカウント
theta_hat_2_values.append(Y / (2 * n))
# 推定量 3: θ̂3 = 平均
theta_hat_3_values = []
for _ in range(n_trials):
U = np.random.uniform(0, 1, n) # 一様分布 [0, 1]
theta_hat_3 = np.mean((1 / np.sqrt(2 * np.pi)) * np.exp(-U**2 / 2))
theta_hat_3_values.append(theta_hat_3)
# ヒストグラムのプロット
plt.figure(figsize=(10, 6))
# ヒストグラム: θ̂1
plt.hist(theta_hat_1_values, bins=30, density=True, alpha=0.5, label='$\\hat{\\theta}_1$', color='blue')
# ヒストグラム: θ̂2
plt.hist(theta_hat_2_values, bins=30, density=True, alpha=0.5, label='$\\hat{\\theta}_2$', color='green')
# ヒストグラム: θ̂3
plt.hist(theta_hat_3_values, bins=30, density=True, alpha=0.5, label='$\\hat{\\theta}_3$', color='orange')
# 理論分布 (正規分布) の線を重ねる
x = np.linspace(0.2, 0.5, 500)
std_theta_hat_1 = np.sqrt(theta * (1 - theta) / n)
std_theta_hat_2 = np.sqrt(2 * theta * (1 - 2 * theta) / (4 * n))
std_theta_hat_3 = np.sqrt(0.0023 / n)
plt.plot(x, norm.pdf(x, loc=theta, scale=std_theta_hat_1), 'b-', label='理論分布 ($\\hat{\\theta}_1$)')
plt.plot(x, norm.pdf(x, loc=theta, scale=std_theta_hat_2), 'g-', label='理論分布 ($\\hat{\\theta}_2$)')
plt.plot(x, norm.pdf(x, loc=theta, scale=std_theta_hat_3), 'r-', label='理論分布 ($\\hat{\\theta}_3$)')
# プロットの設定
plt.title('三つの推定量の分布と理論分布', fontsize=14)
plt.xlabel('推定値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフの表示
plt.show()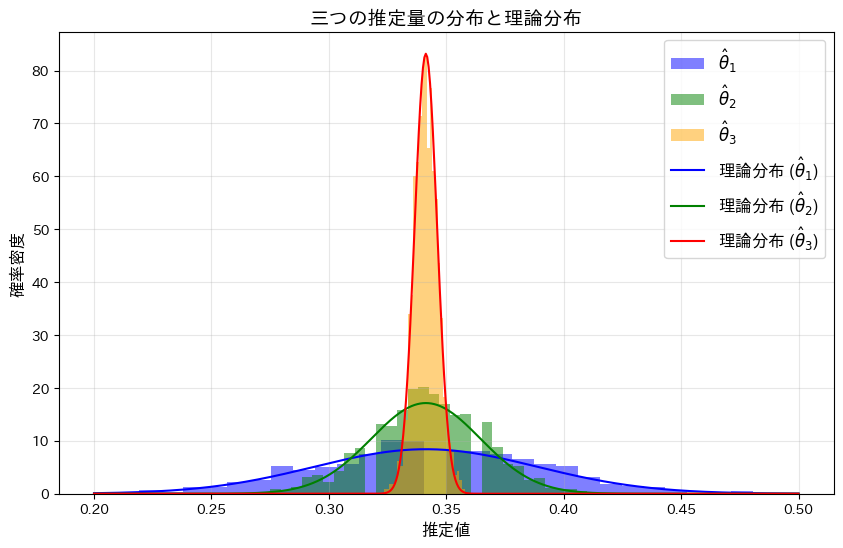
![]() <
<![]() <
<![]() の順にバラつきが小さくなり、分散が最も小さい
の順にバラつきが小さくなり、分散が最も小さい![]() がこの中で最も優れた推定量であることが分かりました。
がこの中で最も優れた推定量であることが分かりました。
2016 Q4(2)
n個の標準正規分布に従う乱数が-1以上1以下となる個数が従う分布を求めました。また乱数が0以上1以下となる確率の推定値の分散を求めました。

コード
この実験では、標準正規分布N(0,1)と、n個の標準正規分布に従う乱数のうち-1以上1以下となる個数Yの分布、およびその確率を推定する量![]() の分布を確認します。
の分布を確認します。
# 2016 Q4(2) 2024.11.24
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, norm
# ---- グラフ 1: 標準正規分布 N(0,1) と範囲 (|Z| < 1) ----
# パラメータの設定
n_samples = 10000 # サンプル数
z_min, z_max = -1, 1 # 条件の範囲 (|Z| < 1)
# 標準正規分布 N(0,1) に従う乱数を生成します
samples = np.random.normal(0, 1, n_samples)
# 理論的な標準正規分布の確率密度関数を計算します
x1 = np.linspace(-4, 4, 500)
pdf_theoretical = norm.pdf(x1, loc=0, scale=1)
# ---- グラフ 2: Y の分布(二項分布) ----
# シミュレーションの設定
n_trials = 1000 # シミュレーションの試行回数
n = 50 # サンプルサイズ (1試行あたりの乱数生成数)
theta = 0.3413 # 真の成功確率 (0 < Z < 1)
# Y の分布を計算
Y_values = []
for _ in range(n_trials):
samples_trial = np.random.normal(0, 1, n)
Y = np.sum((samples_trial > z_min) & (samples_trial < z_max)) # 絶対値が1以下の個数
Y_values.append(Y)
# 理論的な二項分布
p_Y = 2 * theta # |Z| < 1 の確率
x2 = np.arange(0, n + 1)
binomial_pmf_Y = binom.pmf(x2, n, p_Y)
# ---- グラフ 3: θ̂2 の分布と理論分布 ----
# θ̂2 = Y / (2n) を計算
theta_hat_2_values = [Y / (2 * n) for Y in Y_values]
# 理論分布用のデータ
x3 = np.linspace(0, 1, 100)
binomial_pdf_theta_2 = norm.pdf(x3, loc=p_Y / 2, scale=np.sqrt(p_Y * (1 - p_Y) / (4 * n)))
# ---- 3つのグラフを描画 ----
plt.figure(figsize=(10, 12)) # グラフ全体のサイズを指定
# グラフ 1
plt.subplot(3, 1, 1)
plt.hist(samples, bins=50, density=True, alpha=0.5, label='全データ (N(0,1))', color='purple')
plt.axvspan(z_min, z_max, color='orange', alpha=0.3, label='|Z| < 1 の領域')
plt.plot(x1, pdf_theoretical, 'r-', label='理論分布 (N(0,1))', linewidth=2)
plt.title('N(0,1) に従う乱数のヒストグラムと領域', fontsize=14)
plt.xlabel('Z 値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフ 2
plt.subplot(3, 1, 2)
plt.hist(Y_values, bins=np.arange(0, n + 2) - 0.5, density=True, alpha=0.6, color='green', label='Y の分布 (シミュレーション)')
plt.plot(x2, binomial_pmf_Y, 'ro-', label='理論分布 (Binomial)', markersize=4)
plt.title('Y の分布と理論分布の比較', fontsize=14)
plt.xlabel('Y 値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフ 3
plt.subplot(3, 1, 3)
plt.hist(theta_hat_2_values, bins=10, density=True, alpha=0.6, color='blue', label='$\\hat{\\theta}_2$ の分布 (シミュレーション)')
plt.plot(x3, binomial_pdf_theta_2, 'r-', label='理論分布 $N(\\theta, V[\\hat{\\theta}_2])$', linewidth=2)
plt.title('$\\hat{\\theta}_2$ の分布と理論分布の比較', fontsize=14)
plt.xlabel('$\\hat{\\theta}_2$ 値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフを表示
plt.tight_layout() # 全体を整える
plt.show()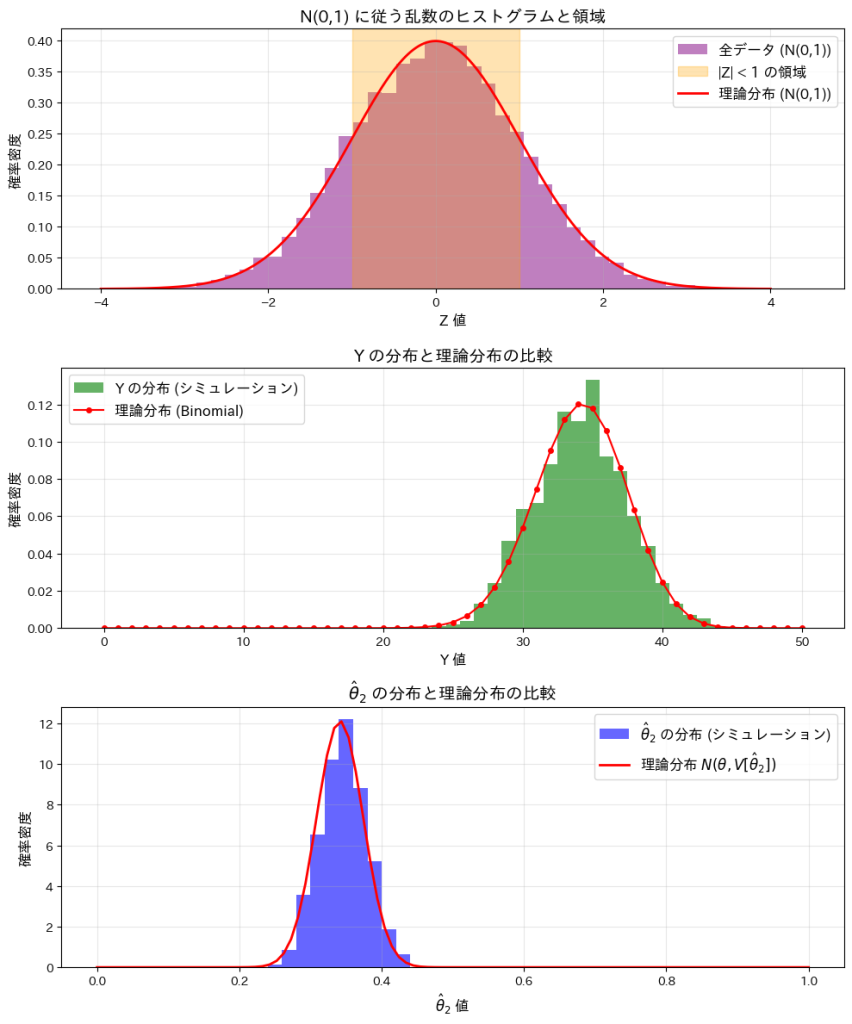
この実験によってYが二項分布B(n,2θ)に従うことと、![]() が正規分布
が正規分布![]() に従うことが確認できました。
に従うことが確認できました。
2016 Q4(1)
n個の標準正規分布に従う乱数が0以上1以下となる個数が従う分布を求めました。また乱数が0以上1以下となる確率の推定値の分散を求めました。

コード
この実験では、標準正規分布N(0,1)と、n個の標準正規分布に従う乱数のうち0以上1以下となる個数Xの分布、およびその確率を推定する量![]() の分布を確認します。
の分布を確認します。
# 2016 Q4(1) 2024.11.23
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom, norm
# ---- グラフ 1: 標準正規分布 N(0,1) と範囲 (0 < Z < 1) ----
# パラメータの設定
n_samples = 10000 # サンプル数
z_min, z_max = 0, 1 # 条件の範囲 (0 < Z < 1)
# 標準正規分布 N(0,1) に従う乱数を生成します
samples = np.random.normal(0, 1, n_samples)
# 理論的な標準正規分布の確率密度関数を計算します
x1 = np.linspace(-4, 4, 500)
pdf_theoretical = norm.pdf(x1, loc=0, scale=1)
# ---- グラフ 2: X の分布(二項分布) ----
# シミュレーションの設定
n_trials = 1000 # シミュレーションの試行回数
n = 50 # サンプルサイズ (1試行あたりの乱数生成数)
theta = 0.3413 # 真の成功確率 (0 < Z < 1)
# X の分布を計算
X_values = []
for _ in range(n_trials):
samples_trial = np.random.normal(0, 1, n)
X = np.sum((samples_trial > z_min) & (samples_trial < z_max))
X_values.append(X)
# 理論的な二項分布
x2 = np.arange(0, n + 1)
binomial_pmf = binom.pmf(x2, n, theta)
# ---- グラフ 3: θ̂1 の分布と理論分布 ----
# θ̂1 = X / n を計算
theta_hat_1_values = [X / n for X in X_values]
# 理論分布用のデータ
x3 = np.linspace(0, 1, 100)
binomial_pdf = norm.pdf(x3, loc=theta, scale=np.sqrt(theta * (1 - theta) / n))
# ---- 3つのグラフを描画 ----
plt.figure(figsize=(10, 10)) # グラフ全体のサイズを指定
# グラフ 1
plt.subplot(3, 1, 1)
plt.hist(samples, bins=50, density=True, alpha=0.5, label='全データ (N(0,1))', color='purple')
plt.axvspan(z_min, z_max, color='orange', alpha=0.3, label='0 < Z < 1 の領域')
plt.plot(x1, pdf_theoretical, 'r-', label='理論分布 (N(0,1))', linewidth=2)
plt.title('N(0,1) に従う乱数のヒストグラムと領域', fontsize=14)
plt.xlabel('Z 値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフ 2
plt.subplot(3, 1, 2)
plt.hist(X_values, bins=np.arange(0, n + 2) - 0.5, density=True, alpha=0.6, color='green', label='X の分布 (シミュレーション)')
plt.plot(x2, binomial_pmf, 'ro-', label='理論分布 (Binomial)', markersize=4)
plt.title('X の分布と理論分布の比較', fontsize=14)
plt.xlabel('X 値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフ 3
plt.subplot(3, 1, 3)
plt.hist(theta_hat_1_values, bins=10, density=True, alpha=0.6, color='blue', label='$\\hat{\\theta}_1$ の分布 (シミュレーション)')
plt.plot(x3, binomial_pdf, 'r-', label='理論分布 $N(\\theta, V[\\hat{\\theta}_1])$', linewidth=2)
plt.title('$\\hat{\\theta}_1$ の分布と理論分布の比較', fontsize=14)
plt.xlabel('$\\hat{\\theta}_1$ 値', fontsize=12)
plt.ylabel('確率密度', fontsize=12)
plt.legend(fontsize=12)
plt.grid(alpha=0.3)
# グラフを表示
plt.tight_layout() # 全体を整える
plt.show()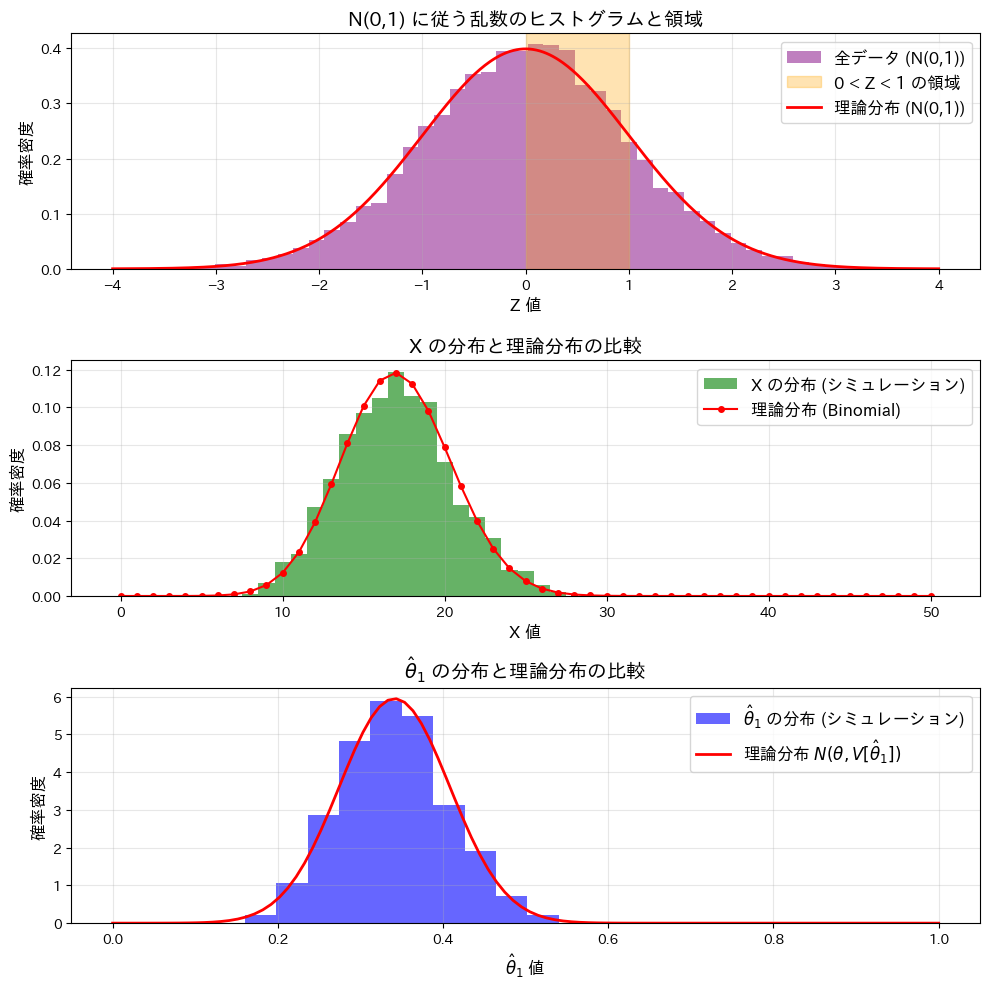
この実験によってXが二項分布B(n,θ)に従うことと、![]() が正規分布
が正規分布![]() に従うことが確認できました。
に従うことが確認できました。
2016 Q3(3)
線形モデルの未知の母数βの3つの不偏推定量の各分散の大小関係を求めました。
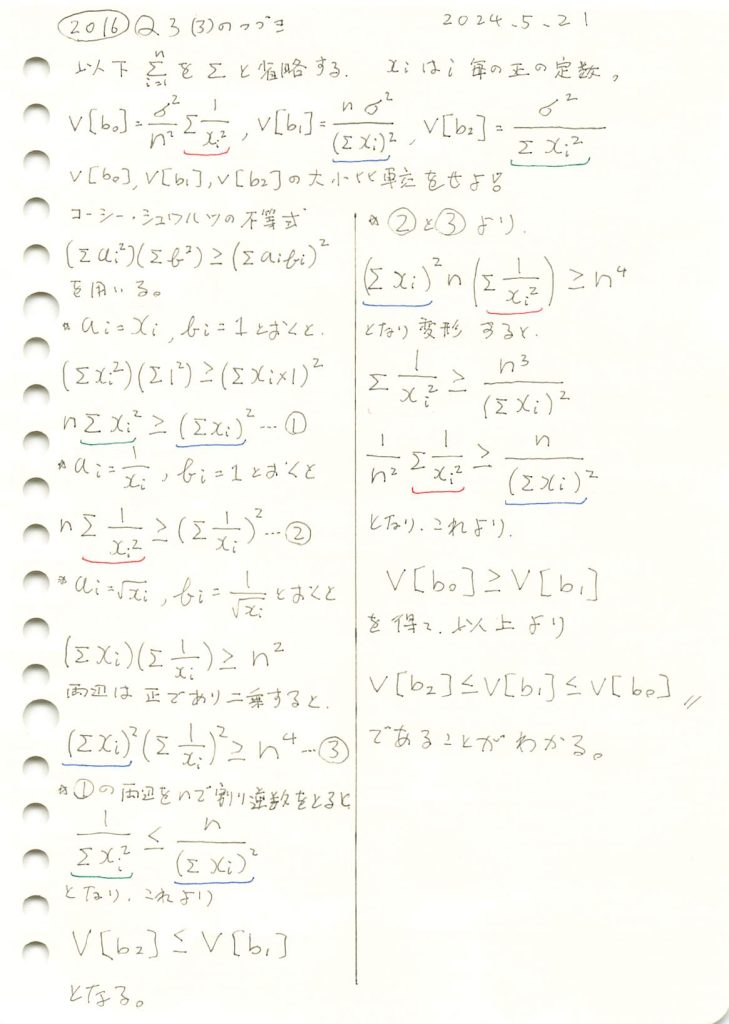
コード
線形モデルのパラメータβの推定量b0,b1,b2の分散の違いを理論式に基づいて確認します。説明変数xiには一様分布に従う値を与え、サンプル数nを変化させて、各推定量の分散の変化を視覚的に比較してみます。ここでは各推定量の違いが分かりやすいように、分散の代わりに標準偏差を視覚化しています。詳しくは前記事(https://statistics.blue/2016-q33/)を参照。
# 2016 Q3(3) 2024.11.22
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 1 # 誤差の標準偏差
true_beta = 2 # 真のβ
sample_sizes = np.arange(10, 101, 10) # サンプルサイズ n を 10 から 100 まで 10 刻みで変化
# 理論的な分散を格納するリスト
variances_b0 = []
variances_b1 = []
variances_b2 = []
# 各サンプルサイズ n に対して分散を計算
for n in sample_sizes:
xi = np.arange(1, n + 1) # 一様に分布した x_i を生成 (例: 1, 2, ..., n)
sum_xi = np.sum(xi)
sum_xi_squared = np.sum(xi**2)
sum_1_over_xi_squared = np.sum(1 / xi**2)
# 分散を理論式で計算
V_b0 = (sigma**2 / n**2) * sum_1_over_xi_squared
V_b1 = (sigma**2 * n) / (sum_xi**2)
V_b2 = sigma**2 / sum_xi_squared
variances_b0.append(V_b0)
variances_b1.append(V_b1)
variances_b2.append(V_b2)
# 理論値からの標準偏差として各分散の平方根を計算
std_b0 = np.sqrt(variances_b0)
std_b1 = np.sqrt(variances_b1)
std_b2 = np.sqrt(variances_b2)
# グラフ作成
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, std_b0, label='$|b_0 - \\beta|$ (標準偏差)', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, std_b1, label='$|b_1 - \\beta|$ (標準偏差)', marker='x', linestyle='dashed', color='orange')
plt.plot(sample_sizes, std_b2, label='$|b_2 - \\beta|$ (標準偏差)', marker='s', linestyle='dashed', color='purple')
plt.axhline(y=0, color='green', linestyle='solid', label='真の値 $\\beta = 2$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('真の値からの標準偏差')
plt.title('推定量 $b_0, b_1, b_2$ の真の値からのずれ(標準偏差)')
plt.legend()
plt.grid(True)
plt.show()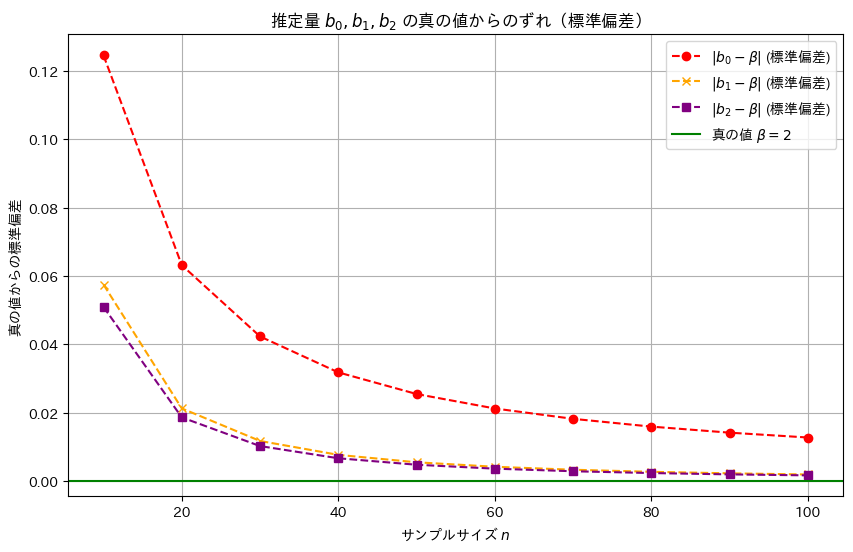
推定量b2,b1,b0の順に標準誤差は小さく、分散も同様の順序で小さくなることが確認できました。この結果から、最小二乗推定量b2が最も効率的であり、推定の安定性が高いことが再確認できました。
2016 Q3(3)
線形モデルの未知の母数βの3つの不偏推定量の各分散を求めました。
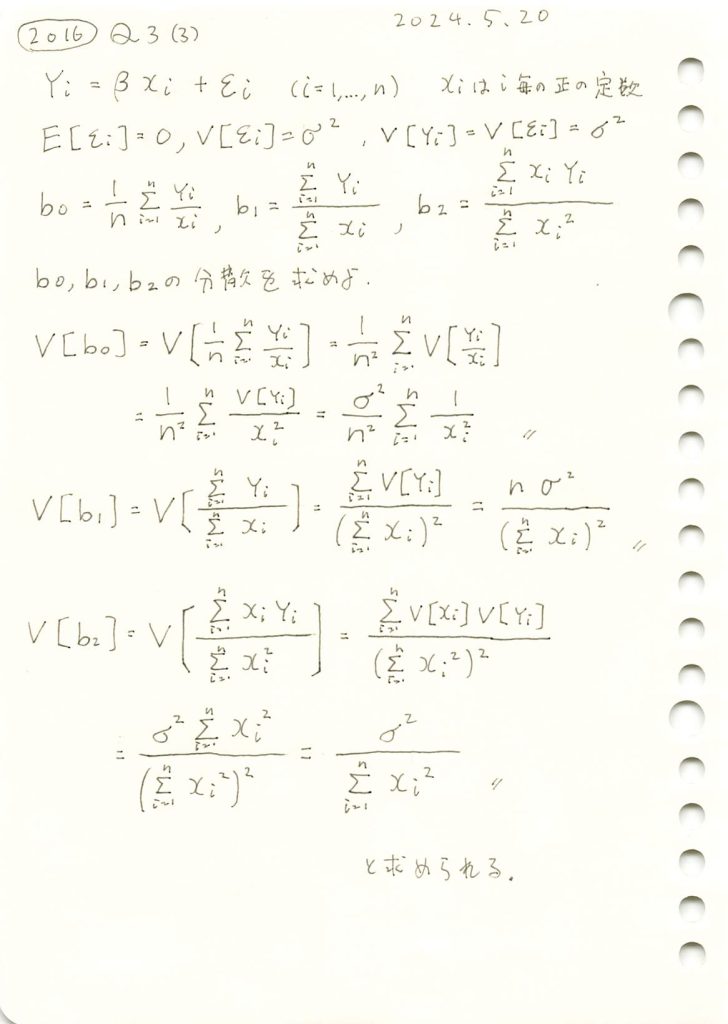
コード
線形モデルのパラメータβの推定量b0,b1,b2の分散の違いを理論式に基づいて確認します。説明変数xiには一様分布に従う値を与え、サンプル数nを変化させて、各推定量の分散の変化を視覚的に比較してみます。
# 2016 Q3(3) 2024.11.22
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 1 # 誤差の標準偏差
sample_sizes = np.arange(10, 101, 10) # サンプルサイズ n を 10 から 100 まで 10 刻みで変化
# 理論的な分散を格納するリスト
variances_b0 = []
variances_b1 = []
variances_b2 = []
# 各サンプルサイズ n に対して分散を計算
for n in sample_sizes:
xi = np.arange(1, n + 1) # 一様に分布した x_i を生成 (例: 1, 2, ..., n)
sum_xi = np.sum(xi)
sum_xi_squared = np.sum(xi**2)
sum_1_over_xi_squared = np.sum(1 / xi**2)
# 分散を理論式で計算
V_b0 = (sigma**2 / n**2) * sum_1_over_xi_squared
V_b1 = (sigma**2 * n) / (sum_xi**2)
V_b2 = sigma**2 / sum_xi_squared
variances_b0.append(V_b0)
variances_b1.append(V_b1)
variances_b2.append(V_b2)
# グラフ作成
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, variances_b0, label='$V[b_0]$', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, variances_b1, label='$V[b_1]$', marker='x', linestyle='dashed', color='orange')
plt.plot(sample_sizes, variances_b2, label='$V[b_2]$', marker='s', linestyle='dashed', color='purple')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('分散')
plt.title('推定量 $b_0$, $b_1$, $b_2$ の理論的分散')
plt.legend()
plt.grid(True)
plt.show()
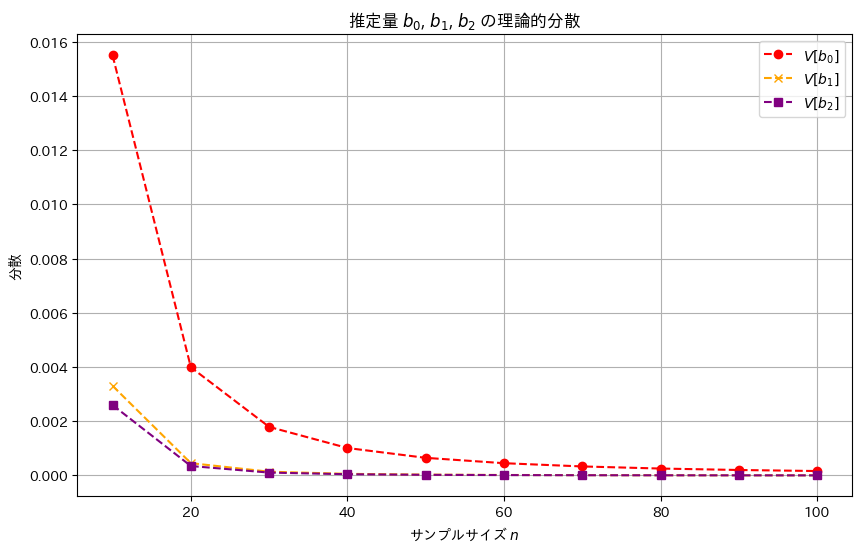
推定量b2,b1,b0の順に分散は小さく見え、b2,b1,b0の順により安定した推定量であることが確認できました。
推定量b1,b2が重なっていて見えづらいため、標準誤差でも視覚化してみます。
# 2016 Q3(3) 2024.11.22
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 1 # 誤差の標準偏差
true_beta = 2 # 真のβ
sample_sizes = np.arange(10, 101, 10) # サンプルサイズ n を 10 から 100 まで 10 刻みで変化
# 理論的な分散を格納するリスト
variances_b0 = []
variances_b1 = []
variances_b2 = []
# 各サンプルサイズ n に対して分散を計算
for n in sample_sizes:
xi = np.arange(1, n + 1) # 一様に分布した x_i を生成 (例: 1, 2, ..., n)
sum_xi = np.sum(xi)
sum_xi_squared = np.sum(xi**2)
sum_1_over_xi_squared = np.sum(1 / xi**2)
# 分散を理論式で計算
V_b0 = (sigma**2 / n**2) * sum_1_over_xi_squared
V_b1 = (sigma**2 * n) / (sum_xi**2)
V_b2 = sigma**2 / sum_xi_squared
variances_b0.append(V_b0)
variances_b1.append(V_b1)
variances_b2.append(V_b2)
# 理論値からの標準偏差として各分散の平方根を計算
std_b0 = np.sqrt(variances_b0)
std_b1 = np.sqrt(variances_b1)
std_b2 = np.sqrt(variances_b2)
# グラフ作成
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, std_b0, label='$|b_0 - \\beta|$ (標準偏差)', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, std_b1, label='$|b_1 - \\beta|$ (標準偏差)', marker='x', linestyle='dashed', color='orange')
plt.plot(sample_sizes, std_b2, label='$|b_2 - \\beta|$ (標準偏差)', marker='s', linestyle='dashed', color='purple')
plt.axhline(y=0, color='green', linestyle='solid', label='真の値 $\\beta = 2$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('真の値からの標準偏差')
plt.title('推定量 $b_0, b_1, b_2$ の真の値からのずれ(標準偏差)')
plt.legend()
plt.grid(True)
plt.show()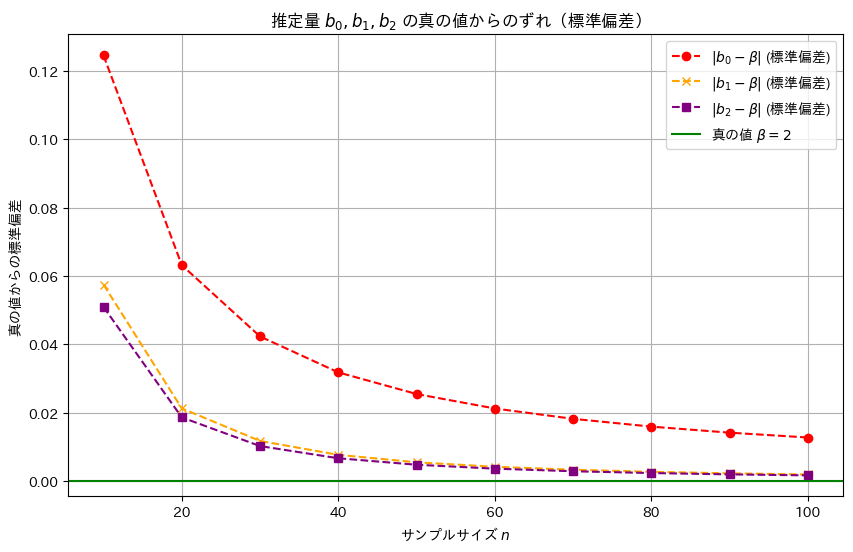
推定量b2,b1,b0の順に標準誤差は小さく、分散も同様の順序で小さくなることが確認できました。この結果から、最小二乗推定量b2が最も効率的であり、推定の安定性が高いことが再確認できました。
2016 Q3(2)
線形モデルの未知の母数βの最小二乗推定量を求め、それが不偏推定量であることを確認しました。
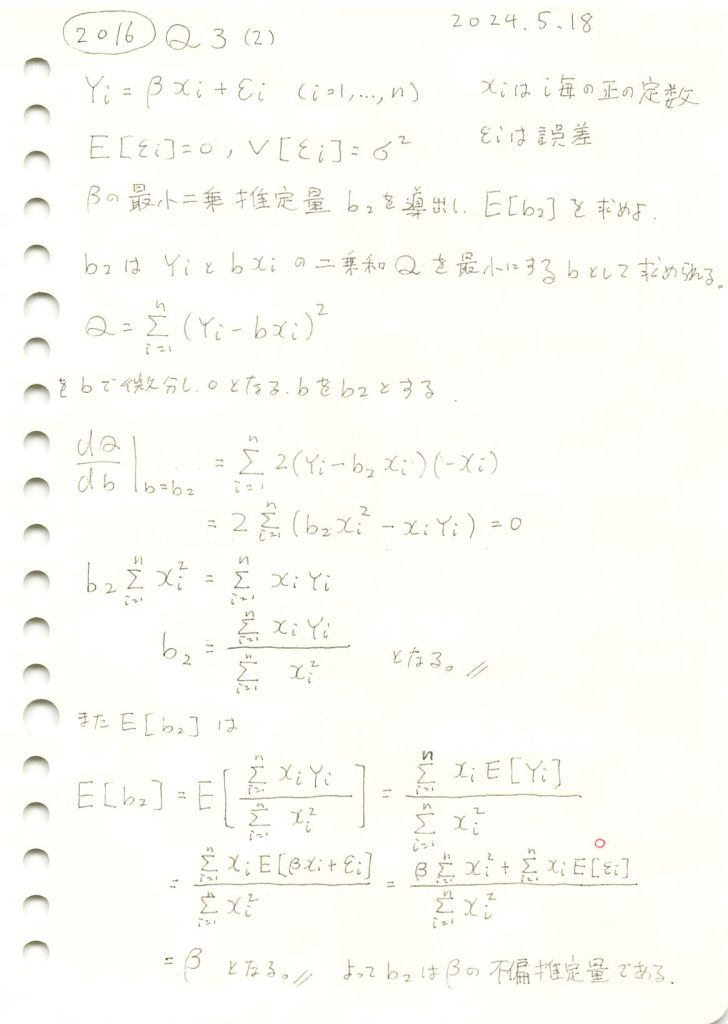
コード
乱数を発生させて線形モデルのパラメータβの推定量b0,b1,b2をそれぞれ計算し、観測データとともにプロットしてみます。推定された直線と真の直線がどのように異なるか視覚的に確認してみます。(b0,b1は前問参照)
# 2016 Q3(2) 2024.11.21
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 10 # サンプルサイズ
true_beta = 2 # 真のβ
sigma = 5 # 誤差の標準偏差
# 1. xi を一様分布から生成
xi = np.random.uniform(1, 10, n)
# 2. εi を正規分布から生成
epsilon_i = np.random.normal(0, sigma, n)
# 3. Yi を計算
Yi = true_beta * xi + epsilon_i
# 4. 推定量 b0, b1 を計算
b0 = np.mean(Yi / xi)
b1 = np.sum(Yi) / np.sum(xi)
# 5. 最小二乗推定量 b2 を計算
b2 = np.sum(xi * Yi) / np.sum(xi**2)
# プロット
plt.figure(figsize=(10, 6))
plt.scatter(xi, Yi, label='観測データ ($Y_i$)', color='blue', marker='x') # マーカーを 'x' に変更
plt.plot(np.sort(xi), true_beta * np.sort(xi), label=f'真の直線 ($\\beta={true_beta}$)', color='green', linestyle='dashed')
plt.plot(np.sort(xi), b0 * np.sort(xi), label=f'推定直線 ($b_0={b0:.2f}$)', color='red')
plt.plot(np.sort(xi), b1 * np.sort(xi), label=f'推定直線 ($b_1={b1:.2f}$)', color='orange')
plt.plot(np.sort(xi), b2 * np.sort(xi), label=f'推定直線 ($b_2={b2:.2f}$)', color='purple')
plt.xlabel('$x_i$')
plt.ylabel('$Y_i$')
plt.title('線形モデルの推定')
plt.legend()
plt.grid(True)
plt.show()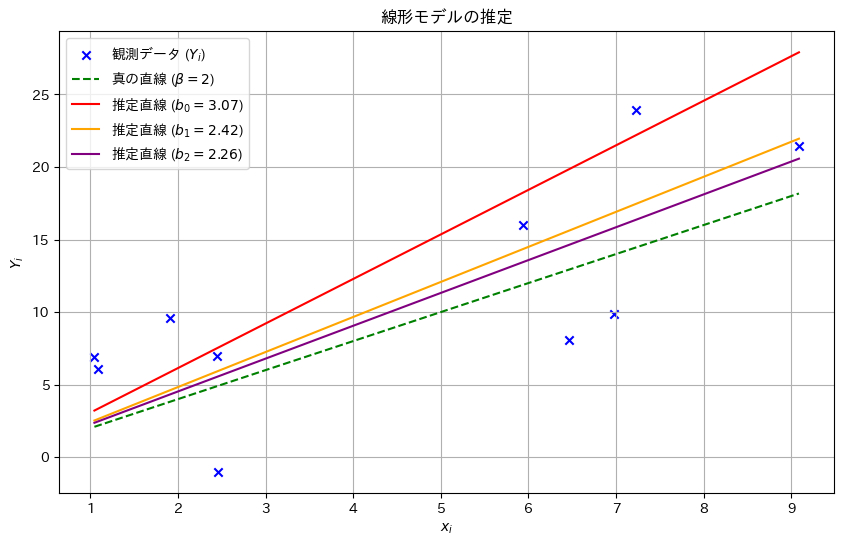
推定量b2,b1,b0の順に真のβに近い値を取りました。
次に、サンプル数nを変化させて、推定量b0,b1,b2がどのように変化するのか観察します
# 2016 Q3(2) 2024.11.21
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma = 5 # 誤差の標準偏差
true_beta = 2 # 真のβ
sample_sizes = np.arange(5, 101, 5) # n を 5 から 100 まで 5 刻みで変化
simulations = 1000 # 各 n に対してのシミュレーション回数
b0_means = []
b1_means = []
b2_means = [] # b2 の期待値を記録
# 各サンプルサイズ n に対してシミュレーションを実行
for n in sample_sizes:
b0_samples = []
b1_samples = []
b2_samples = [] # b2 を記録
for _ in range(simulations):
xi = np.random.uniform(1, 10, n)
epsilon_i = np.random.normal(0, sigma, n)
Yi = true_beta * xi + epsilon_i
b0_samples.append(np.mean(Yi / xi))
b1_samples.append(np.sum(Yi) / np.sum(xi))
b2_samples.append(np.sum(xi * Yi) / np.sum(xi**2)) # b2 を計算
b0_means.append(np.mean(b0_samples))
b1_means.append(np.mean(b1_samples))
b2_means.append(np.mean(b2_samples)) # b2 の期待値を記録
# 結果をプロット
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, b0_means, label='$b_0$の期待値', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, b1_means, label='$b_1$の期待値', marker='x', linestyle='dashed', color='orange')
plt.plot(sample_sizes, b2_means, label='$b_2$の期待値', marker='s', linestyle='dashed', color='purple') # b2 を追加
plt.axhline(y=true_beta, color='green', linestyle='solid', label='真の値 $\\beta=2$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('推定量の期待値')
plt.title('推定量 $b_0, b_1, b_2$ の期待値とサンプルサイズの関係')
plt.legend()
plt.grid(True)
plt.show()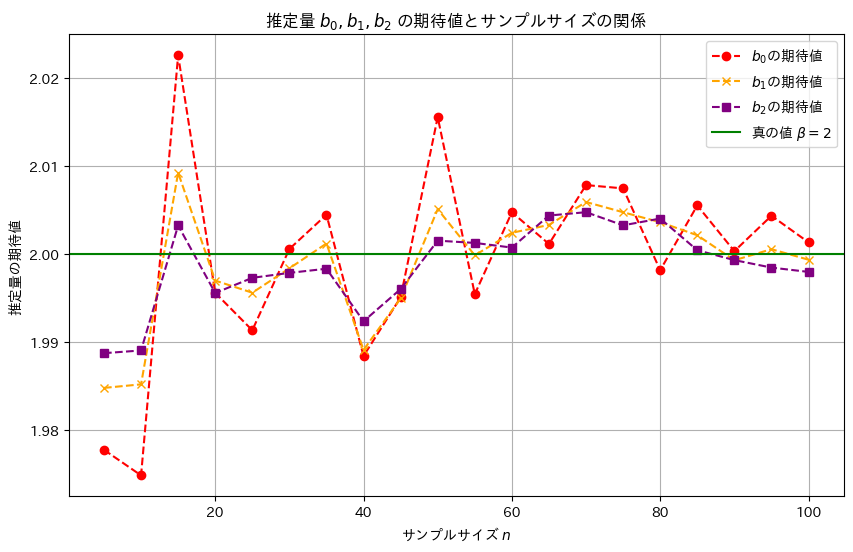
サンプルサイズnが大きくなるほど、推定量b0,b1,b2は真の値βに近づくことが確認できました。また、推定量b2,b1,b0の順に分散は小さく見え、b2,b1,b0の順により安定した推定量のようです。
次に、推定量b0,b1,b2の分布を確認してみます。それぞれのヒストグラムを重ねて表示してみます。
# 2016 Q3(2) 2024.11.21
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 100 # サンプルサイズ
true_beta = 2 # 真のβ
sigma = 1 # 誤差の標準偏差
simulations = 10000 # シミュレーション回数
b0_samples = []
b1_samples = []
b2_samples = [] # b2 の分布を記録
# シミュレーションを実施
for _ in range(simulations):
xi = np.random.uniform(1, 10, n)
epsilon_i = np.random.normal(0, sigma, n)
Yi = true_beta * xi + epsilon_i
b0_samples.append(np.mean(Yi / xi))
b1_samples.append(np.sum(Yi) / np.sum(xi))
b2_samples.append(np.sum(xi * Yi) / np.sum(xi**2)) # b2 を計算
# b0, b1, b2 の分布を重ねてプロット
plt.figure(figsize=(10, 6))
plt.hist(b0_samples, bins=30, density=True, color='red', alpha=0.5, label='$b_0$')
plt.hist(b1_samples, bins=30, density=True, color='orange', alpha=0.5, label='$b_1$')
plt.hist(b2_samples, bins=30, density=True, color='purple', alpha=0.5, label='$b_2$') # b2 を追加
plt.axvline(x=true_beta, color='green', linestyle='dashed', label='真の値 $\\beta=2$')
plt.title('$b_0$, $b_1$, $b_2$ の分布 (n=100)')
plt.xlabel('推定値')
plt.ylabel('頻度')
plt.legend()
plt.grid(True)
plt.show()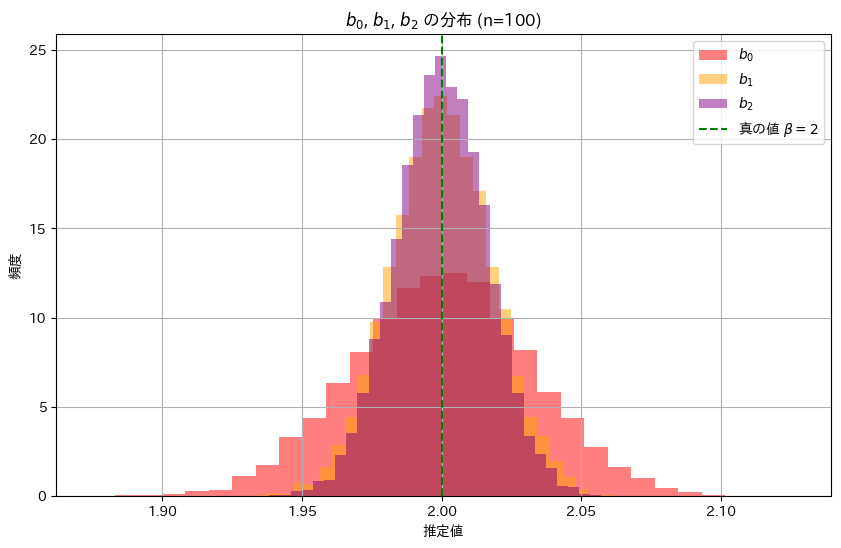
推定量b2,b1,b0の順に幅が狭く、分散が小さいことが確認できました。これにより推定量b2,b1,b0の順に安定した推定であることが分かりました。
2016 Q3(1)
線形モデルの未知の母数βの2つの推定量が不偏推定量であることを確認しました。

コード
乱数を発生させて線形モデルのパラメータβの推定量b0,b1をそれぞれ求め、観測データとともにプロットしてみます。推定された直線と真の直線がどのように異なるか視覚的に確認してみます。
# 2016 Q3(1) 2024.11.20
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 50 # サンプルサイズ
true_beta = 2 # 真のβ
sigma = 5 # 誤差の標準偏差
# 1. xi を一様分布から生成
xi = np.random.uniform(1, 10, n)
# 2. εi を正規分布から生成
epsilon_i = np.random.normal(0, sigma, n)
# 3. Yi を計算
Yi = true_beta * xi + epsilon_i
# 4. 推定量 b0, b1 を計算
b0 = np.mean(Yi / xi)
b1 = np.sum(Yi) / np.sum(xi)
# プロット
plt.figure(figsize=(10, 6))
plt.scatter(xi, Yi, label='観測データ ($Y_i$)', color='blue', marker='x')
plt.plot(np.sort(xi), true_beta * np.sort(xi), label=f'真の直線 ($\\beta={true_beta}$)', color='green', linestyle='dashed')
plt.plot(np.sort(xi), b0 * np.sort(xi), label=f'推定直線 ($b_0={b0:.2f}$)', color='red')
plt.plot(np.sort(xi), b1 * np.sort(xi), label=f'推定直線 ($b_1={b1:.2f}$)', color='orange')
plt.xlabel('$x_i$')
plt.ylabel('$Y_i$')
plt.title('線形モデルの推定')
plt.legend()
plt.grid(True)
plt.show()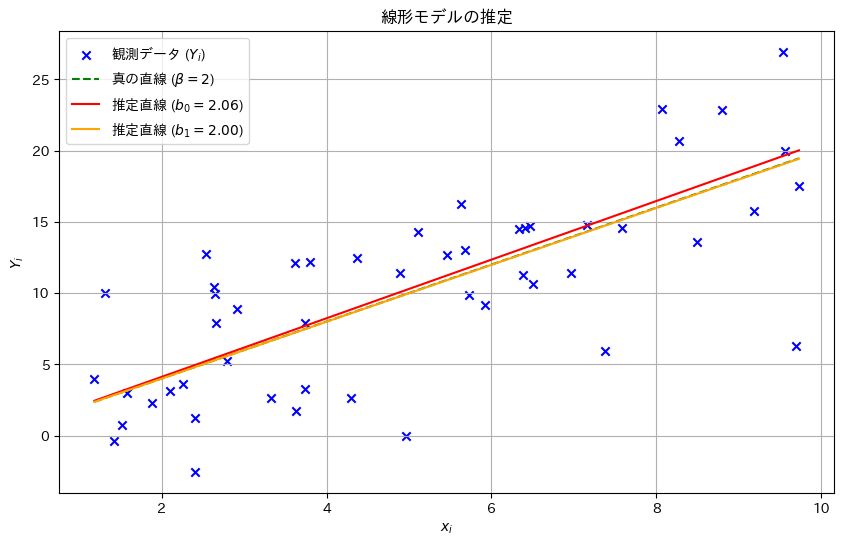
b0とb1は真のβに近い値を取り、直線は概ね一致しました。
次に、サンプル数nを変化させて、推定量b0,b1がどのように変化するのか観察します
# 2016 Q3(1) 2024.11.20
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 50 # サンプルサイズ
true_beta = 2 # 真のβ
sigma = 5 # 誤差の標準偏差
# サンプルサイズを変化させて b0, b1 の期待値を検証
sample_sizes = np.arange(5, 101, 5) # n を 5 から 100 まで 5 刻みで変化
true_beta = 2 # 真のβ
simulations = 1000 # 各 n に対してのシミュレーション回数
b0_means = []
b1_means = []
# 各サンプルサイズ n に対してシミュレーションを実行
for n in sample_sizes:
b0_samples = []
b1_samples = []
for _ in range(simulations):
xi = np.random.uniform(1, 10, n)
epsilon_i = np.random.normal(0, sigma, n)
Yi = true_beta * xi + epsilon_i
b0_samples.append(np.mean(Yi / xi))
b1_samples.append(np.sum(Yi) / np.sum(xi))
b0_means.append(np.mean(b0_samples))
b1_means.append(np.mean(b1_samples))
# 結果をプロット
plt.figure(figsize=(10, 6))
plt.plot(sample_sizes, b0_means, label='$b_0$の期待値', marker='o', linestyle='dashed', color='red')
plt.plot(sample_sizes, b1_means, label='$b_1$の期待値', marker='x', linestyle='dashed', color='orange')
plt.axhline(y=true_beta, color='green', linestyle='solid', label='真の値 $\\beta=2$')
plt.xlabel('サンプルサイズ $n$')
plt.ylabel('推定量の期待値')
plt.title('推定量 $b_0, b_1$ の期待値とサンプルサイズの関係')
plt.legend()
plt.grid(True)
plt.show()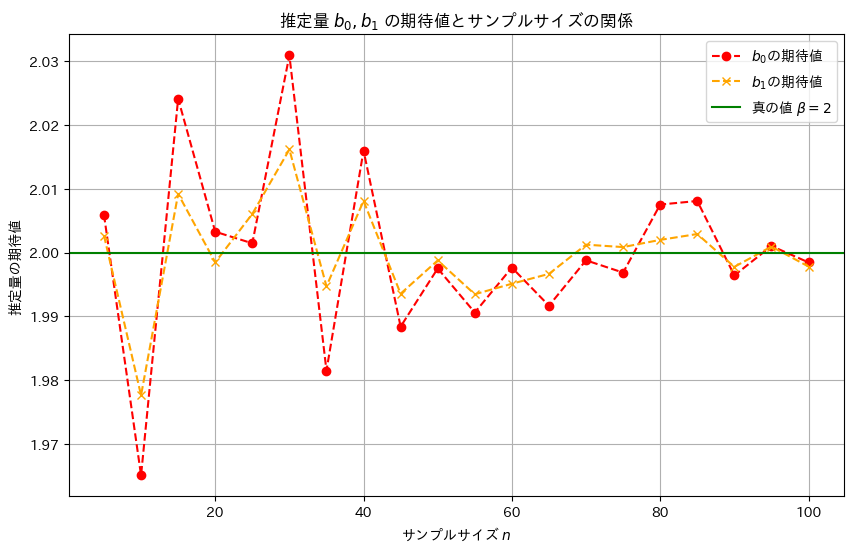
サンプルサイズnが大きくなるほど、推定量b0,b1は真の値βに近づくことが確認できました。また、b1の分散はb0の分散より小さく見え、b1はb0より安定した推定量のようです。
次に、推定量b0,b1の分布を確認してみます。それぞれのヒストグラムを重ねて表示してみます。
# 2016 Q3(1) 2024.11.20
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 100 # サンプルサイズ
true_beta = 2 # 真のβ
sigma = 1 # 誤差の標準偏差
simulations = 10000 # シミュレーション回数
b0_samples = []
b1_samples = []
# シミュレーションを実施
for _ in range(simulations):
xi = np.random.uniform(1, 10, n)
epsilon_i = np.random.normal(0, sigma, n)
Yi = true_beta * xi + epsilon_i
b0_samples.append(np.mean(Yi / xi))
b1_samples.append(np.sum(Yi) / np.sum(xi))
# b0 と b1 の分布を重ねてプロット
plt.figure(figsize=(10, 6))
plt.hist(b0_samples, bins=30, density=True, color='red', alpha=0.5, label='$b_0$')
plt.hist(b1_samples, bins=30, density=True, color='orange', alpha=0.5, label='$b_1$')
plt.axvline(x=true_beta, color='green', linestyle='dashed', label='真の値 $\\beta=2$')
plt.title('$b_0$ と $b_1$ の分布 (n=100)')
plt.xlabel('推定値')
plt.ylabel('頻度')
plt.legend()
plt.grid(True)
plt.show()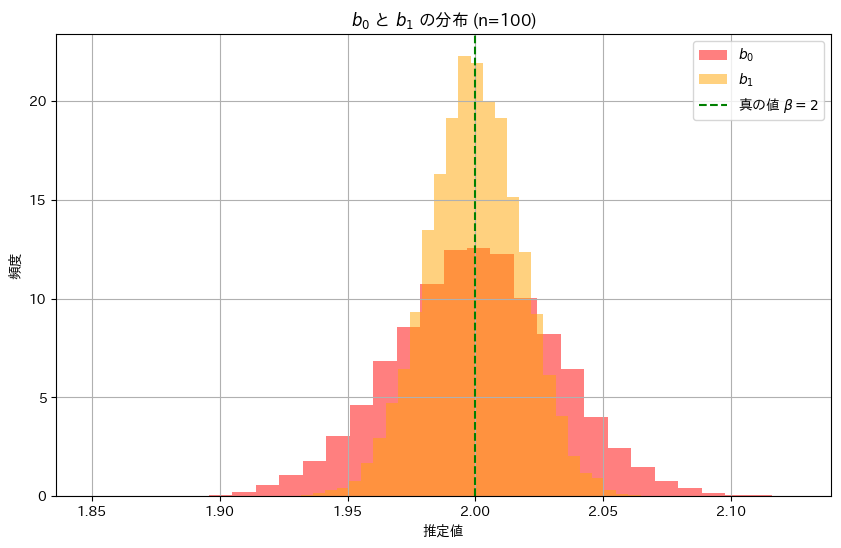
推定量b1の分布は、推定量b0の分布に比べて幅が狭く、b1の分散のほうがb0よりも小さく、安定した推定であることが分かりました。