ホーム » コードあり (ページ 14)
「コードあり」カテゴリーアーカイブ
2019 Q2(1)
独立な指数分布に従う2変数の和の期待値を求めました。
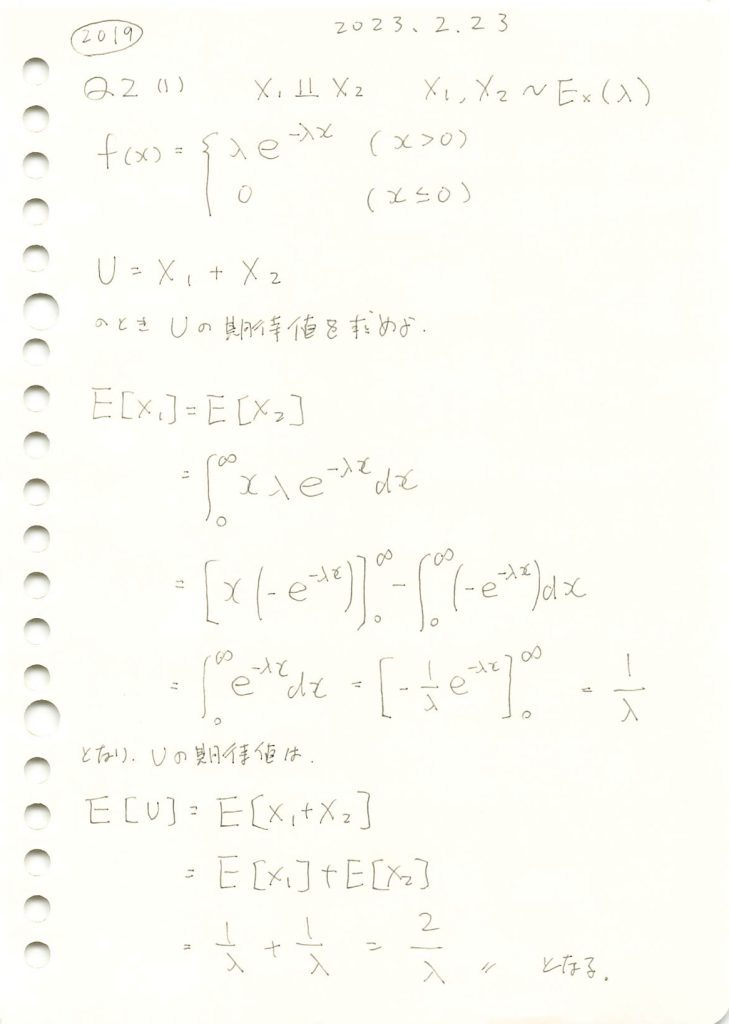
コード
数式を使ってUの期待値を求めます
import sympy as sp
# 変数の定義
x = sp.Symbol('x', positive=True)
lambda_value = sp.Symbol('lambda', positive=True)
# 指数分布の確率密度関数 (PDF)
f_x = lambda_value * sp.exp(-lambda_value * x)
# 期待値の式を計算 (積分)
E_X1 = sp.integrate(x * f_x, (x, 0, sp.oo))
# 期待値
E_X1_simplified = sp.simplify(E_X1)
# X1 + X2 の場合 (独立性より)
E_U = 2 * E_X1_simplified
# 結果の表示
display(E_U)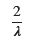
手計算と一致します
次にUに従う乱数を生成し分布を確認します。また形状パラメータ2のガンマ分布と重ねて描画します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # 例としてλ=2
num_samples = 1000 # サンプルの数
# 指数分布に従う乱数の生成
X1 = np.random.exponential(scale=1/lambda_value, size=num_samples)
X2 = np.random.exponential(scale=1/lambda_value, size=num_samples)
# U = X1 + X2 の計算
U = X1 + X2
# 理論的な期待値
expected_value = 2 / lambda_value
# シミュレーション結果のヒストグラムのプロット (確率密度にスケール)
plt.hist(U, bins=30, density=True, alpha=0.7, label='シミュレーション結果')
# ガンマ分布 (形状パラメータ k=2, スケールパラメータ θ=1/λ) の確率密度関数 (PDF) を計算
k = 2 # 形状パラメータ (k = 2)
theta = 1 / lambda_value # スケールパラメータ (θ = 1/λ)
# ガンマ分布に基づくx軸の範囲
x = np.linspace(0, max(U), 1000)
# ガンマ分布の確率密度関数 (PDF) を計算
gamma_pdf = gamma.pdf(x, a=k, scale=theta)
# ガンマ分布の折れ線グラフをプロット
plt.plot(x, gamma_pdf, 'r-', label=f'ガンマ分布 (k={k}, θ={theta:.2f})')
# グラフの装飾
plt.axvline(expected_value, color='g', linestyle='--', label=f'理論値 = {expected_value:.2f}')
plt.xlabel('U = X1 + X2')
plt.ylabel('確率密度')
plt.title('Uの分布とガンマ分布の比較')
plt.legend()
plt.show()
# 実際のサンプル平均値と理論的期待値の比較
print(f'理論的な期待値: {expected_value}')
print(f'シミュレーションからの平均値: {np.mean(U)}')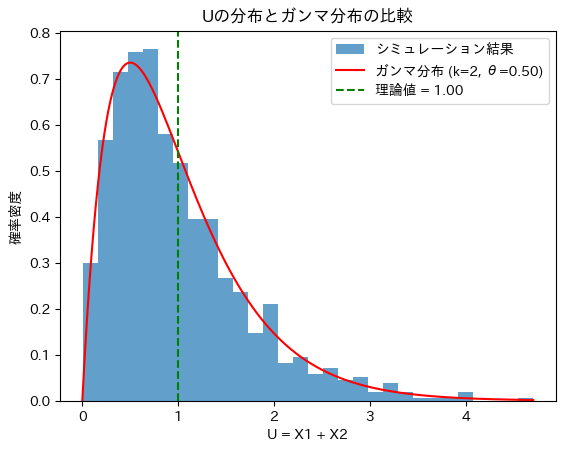
理論的な期待値: 1.0
シミュレーションからの平均値: 0.9902440726761544Uの分布と形状パラメータ2のガンマ分布は重なりました。Uはガンマ分布に従うことが分かります。
2021 Q3(1)
ポアソン分布のモーメント母関数を求めました。
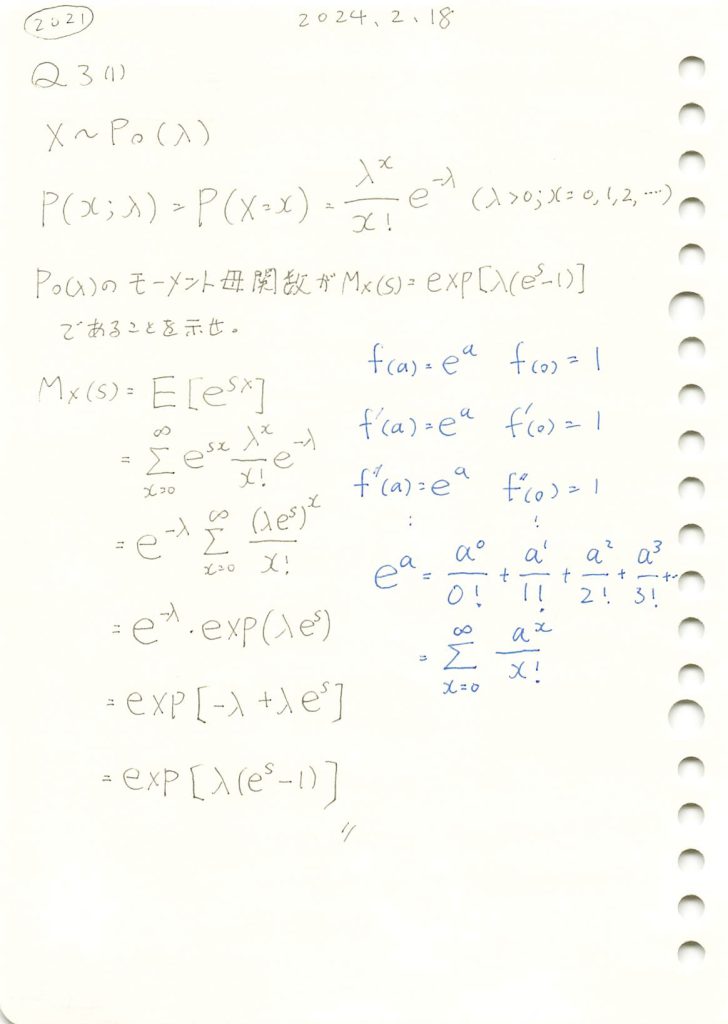
コード
数式を使った計算
# 2021 Q3(1) 2024.8.25
import sympy as sp
# 変数の定義
s, x, lambda_ = sp.symbols('s x lambda_', real=True, positive=True)
# ポアソン分布の確率質量関数 (PMF)
poisson_pmf = (lambda_**x * sp.exp(-lambda_)) / sp.factorial(x)
# モーメント母関数 M_X(s) の定義
M_X = sp.summation(sp.exp(s*x) * poisson_pmf, (x, 0, sp.oo))
# 結果を簡略化
M_X_simplified = sp.simplify(M_X)
# 結果を表示
M_X_simplified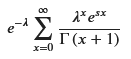
無限級数がe^xの形に変換されないようです。
exp(s) を t に置き換えて、最後に戻してみます。
# 2021 Q3(1) 2024.8.25
import sympy as sp
# 変数の定義
s, x, lambda_, t = sp.symbols('s x lambda_ t', real=True, positive=True)
# exp(s) を t に置き換え
summand = (lambda_ * t)**x / sp.factorial(x)
# モーメント母関数 M_X(s) の定義
M_X = sp.exp(-lambda_) * sp.summation(summand, (x, 0, sp.oo))
# 簡略化
M_X_simplified = sp.simplify(M_X)
# 最後に t を exp(s) に戻す
M_X_final = M_X_simplified.subs(t, sp.exp(s))
# 結果を表示
M_X_final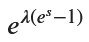
手計算と同じ形になりました。
モーメント母関数を使って期待値と分散を求めます。
import sympy as sp
# 変数の定義
s, lambda_ = sp.symbols('s lambda_', real=True, positive=True)
# モーメント母関数 M_X(s) の定義
M_X = sp.exp(lambda_ * (sp.exp(s) - 1))
# 1次モーメント(期待値)の計算
M_X_prime = sp.diff(M_X, s)
expectation = M_X_prime.subs(s, 0)
# 2次モーメントの計算
M_X_double_prime = sp.diff(M_X_prime, s)
second_moment = M_X_double_prime.subs(s, 0)
# 分散の計算
variance = second_moment - expectation**2
# 結果を表示
display(expectation, variance)
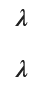
2021 Q2(4)
事前分布と尤度から事後確率が最大となるパラメータの推定値を求めました。

コード
数式を使った計算
# 2021 Q2(4) 2024.8.24
import numpy as np
from scipy.special import comb
# 事前分布 P(N_A)
def prior(NA):
return NA + 1
# 尤度関数 P(X = 4 | N_A)
def likelihood(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# 事後分布 P(N_A | X = 4) (正規化定数は省略)
def posterior(NA):
return prior(NA) * likelihood(NA)
# N_A の範囲
NA_values = np.arange(4, 90)
# 事後分布の計算
posterior_values = [posterior(NA) for NA in NA_values]
# 最大値を取る N_A (事後モード) を探索
NA_mode = NA_values[np.argmax(posterior_values)]
NA_mode30プロット
# 2021 Q2(4) 2024.8.24
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
# 事前分布 P(N_A)
def prior(NA):
return NA + 1
# 正規化定数
C = 1 / 5151
# 尤度関数 P(X = 4 | N_A)
def likelihood(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# 事後分布 P(N_A | X = 4)
def posterior(NA):
return prior(NA) * likelihood(NA)
# N_A の範囲を0から100まで(事前分布用)
NA_values_full = np.arange(0, 101)
# 事前分布を計算(0から100まで)
prior_values_full = [C * prior(NA) for NA in NA_values_full]
# N_A の範囲を4から89まで(事後分布用)
NA_values = np.arange(4, 90)
# 事後分布の計算
posterior_values = [posterior(NA) for NA in NA_values]
# 事後分布の正規化
posterior_sum = sum(posterior_values)
posterior_values_normalized = [value / posterior_sum for value in posterior_values]
# 事前分布が存在しない場合の事後分布(尤度のみを正規化)
likelihood_values = [likelihood(NA) for NA in NA_values]
likelihood_sum = sum(likelihood_values)
likelihood_values_normalized = [value / likelihood_sum for value in likelihood_values]
# 3つの分布を重ねて表示
plt.figure(figsize=(10, 6))
# 事前分布のプロット(0から100まで)
plt.plot(NA_values_full, prior_values_full, 'g-', label=r'事前分布 $P(N_A)$', markersize=5)
# 事後分布のプロット(4から89まで)
plt.plot(NA_values, posterior_values_normalized, 'bo-', label=r'事後分布 $P(N_A | X = 4)$', markersize=5)
# 事前分布が存在しない場合の事後分布(尤度のみ)
plt.plot(NA_values, likelihood_values_normalized, 'r-', label=r'事前分布なし $P(N_A | X = 4)$', markersize=5)
# 事後モードのプロット
NA_mode = NA_values[np.argmax(posterior_values_normalized)]
plt.axvline(NA_mode, color='blue', linestyle='--', label=f'事後モード: {NA_mode}')
# 事前分布なしの場合の最尤推定値のプロット
NA_mode_likelihood = NA_values[np.argmax(likelihood_values_normalized)]
plt.axvline(NA_mode_likelihood, color='red', linestyle=':', label=f'最尤推定値 (事前分布なし): {NA_mode_likelihood}')
# グラフの設定
plt.xlabel(r'$N_A$')
plt.ylabel(r'確率')
plt.title(r'事前分布ありとなしの比較')
plt.grid(True)
plt.legend()
plt.show()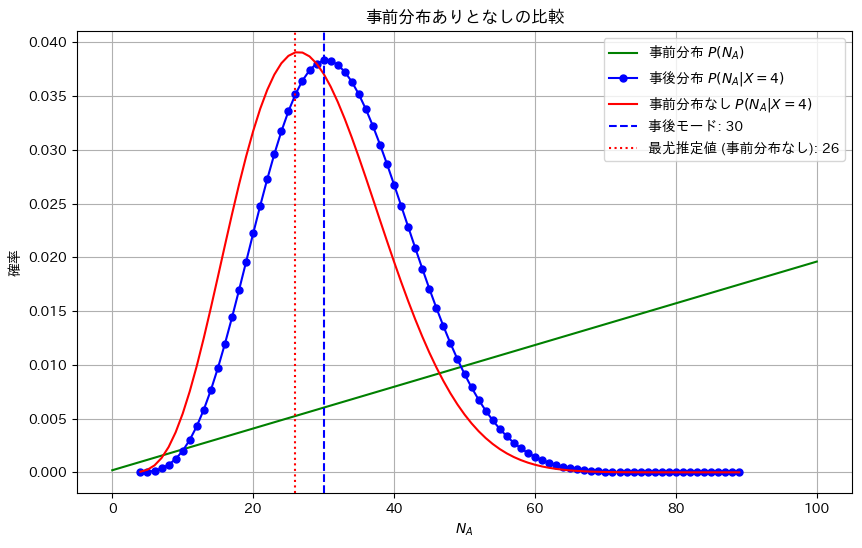
2021 Q2(3)
離散型確率分布の正規化定数を計算しました。

コード
数式を使った計算
# 2021 Q2(3) 2024.8.23
from sympy import symbols, summation, Eq, solve
# 記号の定義
n = symbols('n', integer=True)
C = symbols('C', real=True)
# 和を計算
sum_expr = summation(C * (n + 1), (n, 0, 100))
# 正規化条件を設定
normalization_condition = Eq(sum_expr, 1)
# C を解く
C_value = solve(normalization_condition, C)[0]
C_value
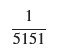
P(N_A = n)のプロット
# 2021 Q2(3) 2024.8.23
import matplotlib.pyplot as plt
import numpy as np
# 正規化定数 C
C_value = 1 / 5151
# n の範囲
n_values = np.arange(0, 101)
# 確率質量関数 P(N_A = n)
pmf_values = C_value * (n_values + 1)
# グラフの描画
plt.figure(figsize=(10, 6))
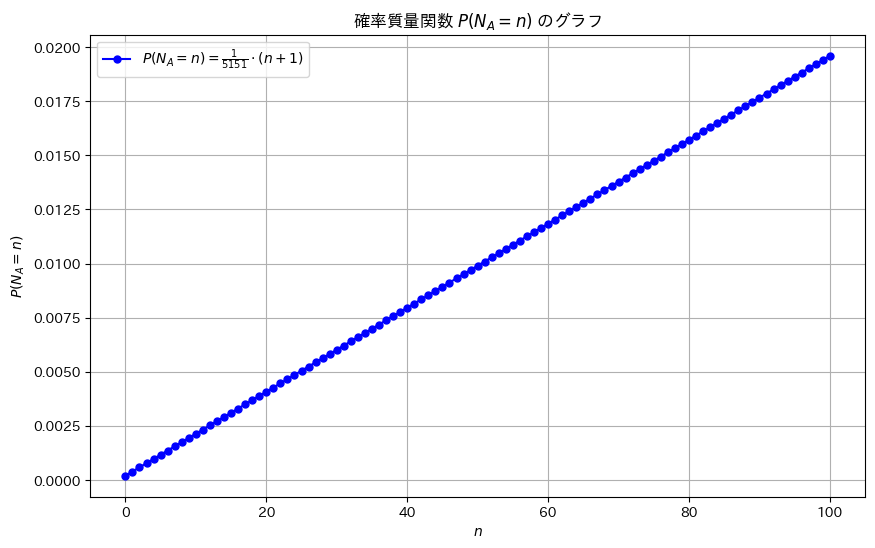
plt.plot(n_values, pmf_values, 'bo-', label=r'$P(N_A = n) = \frac{1}{5151} \cdot (n + 1)$', markersize=5)
plt.xlabel(r'$n$')
plt.ylabel(r'$P(N_A = n)$')
plt.title(r'確率質量関数 $P(N_A = n)$ のグラフ')
plt.grid(True)
plt.legend()
plt.show()
2021 Q2(2)
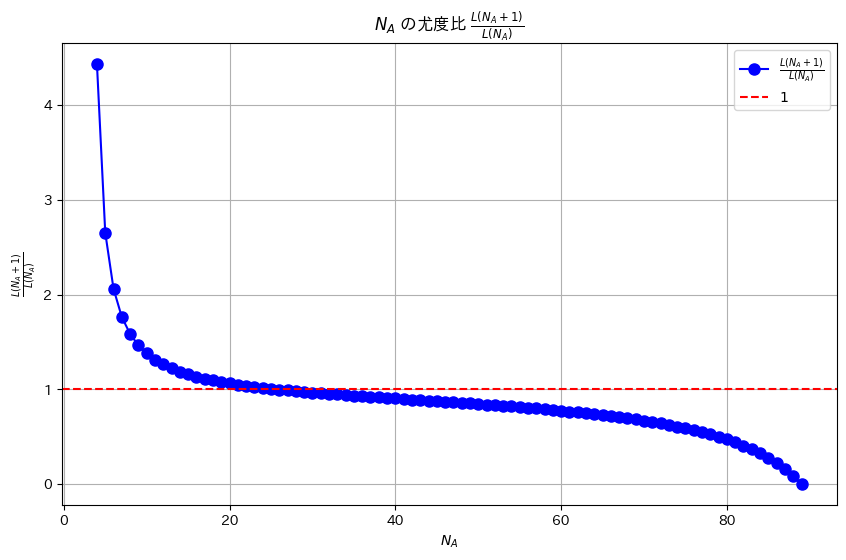
超幾何分布の当たりの数の推定値を尤度比を使って求めました。

コード
シミュレーションによる計算
# 2021 Q2(2) 2024.8.22
import numpy as np
from scipy.special import comb
# 尤度関数 L(N_A) を定義
def L(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# L(N_A + 1) / L(N_A) を計算し、条件を満たす最小の N_A を探索
# max(0, N_A - 85) ≤ 4 ≤ min(15, N_A) の式に基づき、取り出した豆Aが4粒の場合の N_A の範囲を設定 (4 ≤ N_A ≤ 89)
NA_values = np.arange(4, 90)
ratios = [(L(NA + 1) / L(NA)) for NA in NA_values]
NA_optimal = NA_values[np.where(np.array(ratios) < 1)[0][0]]
print(f"L(N_A + 1) / L(N_A) < 1 となる最小の N_A は {NA_optimal} です。")
L(N_A + 1) / L(N_A) < 1 となる最小の N_A は 26 です。プロット
# 2021 Q2(2) 2024.8.22
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
# 尤度関数 L(N_A) を定義
def L(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# N_A の範囲を設定
NA_values = np.arange(4, 90)
ratios = [(L(NA + 1) / L(NA)) for NA in NA_values]
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(NA_values, ratios, 'bo-', label=r'$\frac{L(N_A + 1)}{L(N_A)}$', markersize=8)
plt.axhline(y=1, color='red', linestyle='--', label=r'$1$')
plt.xlabel(r'$N_A$')
plt.ylabel(r'$\frac{L(N_A + 1)}{L(N_A)}$')
plt.title(r'$N_A$ の尤度比 $\frac{L(N_A + 1)}{L(N_A)}$')
plt.legend()
plt.grid(True)
plt.show()
プロット(NA=26付近をズーム)
# 2021 Q2(2) 2024.8.22
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
# 尤度関数 L(N_A) を定義
def L(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# N_A の範囲を設定
NA_values = np.arange(4, 90)
ratios = [(L(NA + 1) / L(NA)) for NA in NA_values]
# 26付近のズームしたグラフを描画
plt.figure(figsize=(10, 6))
plt.plot(NA_values, ratios, 'bo-', label=r'$\frac{L(N_A + 1)}{L(N_A)}$', markersize=8)
plt.axhline(y=1, color='red', linestyle='--', label=r'$1$')
plt.xlabel(r'$N_A$')
plt.ylabel(r'$\frac{L(N_A + 1)}{L(N_A)}$')
plt.title(r'$N_A$ の尤度比 $\frac{L(N_A + 1)}{L(N_A)}$ (25 < $N_A$ < 30)')
plt.xlim(25, 30) # N_A = 26 付近をズーム
plt.ylim(0.95, 1.05) # y軸もズームして見やすく
plt.legend()
plt.grid(True)
plt.show()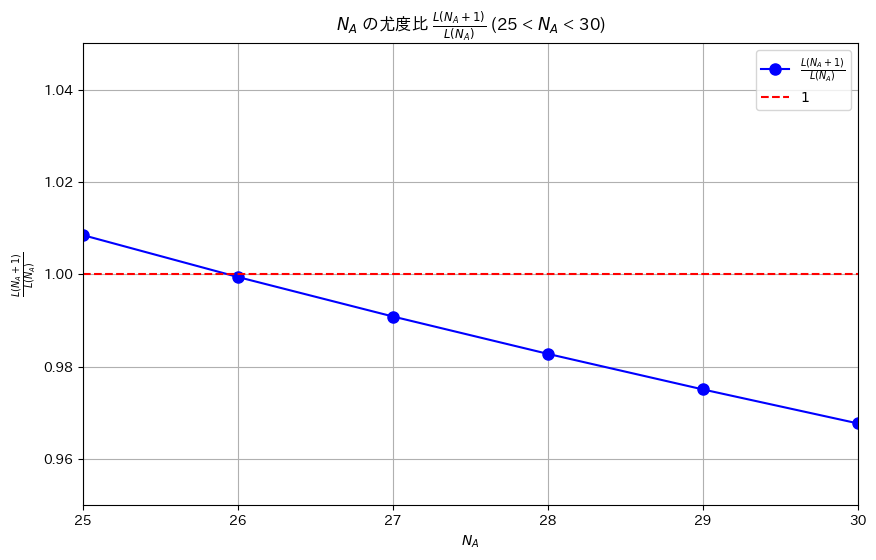
2021 Q2(1)
超幾何分布の問題をやりました。

コード
シミュレーションによる計算
# 2021 Q2(1) 2024.8.21
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import hypergeom
# パラメータの設定
M = 100 # 全体の豆の数
N_A = 30 # 豆Aの数
n = 15 # 抽出する豆の数
x_values = np.arange(0, n+1) # 可能な豆Aの数
# 理論的な超幾何分布のPMFを計算
rv = hypergeom(M, N_A, n)
pmf_theoretical = rv.pmf(x_values)
# 数値シミュレーションの設定
n_simulations = 10000 # シミュレーション回数
simulated_counts = []
# シミュレーションの実行
for _ in range(n_simulations):
# 袋の中の豆を表すリスト(1が豆A、0が豆B)
bag = np.array([1]*N_A + [0]*(M - N_A))
# 無作為に15個抽出
sample = np.random.choice(bag, size=n, replace=False)
# 抽出した中の豆Aの数をカウント
count_A = np.sum(sample)
simulated_counts.append(count_A)
# シミュレーションから得られたPMFを計算
pmf_simulated, bins = np.histogram(simulated_counts, bins=np.arange(-0.5, n+1.5, 1), density=True)
# グラフの描画
plt.figure(figsize=(10, 6))
# 理論的なPMFの描画
plt.plot(x_values, pmf_theoretical, 'bo-', label='理論的PMF', markersize=8)
# シミュレーション結果をヒストグラムとして描画
plt.hist(simulated_counts, bins=np.arange(-0.5, n+1.5, 1), density=True, alpha=0.5, color='red', label='シミュレーション結果')
# グラフの設定
plt.xlabel('豆Aの数')
plt.ylabel('確率')
plt.title('超幾何分布のPMF: 理論とシミュレーションの比較')
plt.legend()
plt.grid(True)
plt.show()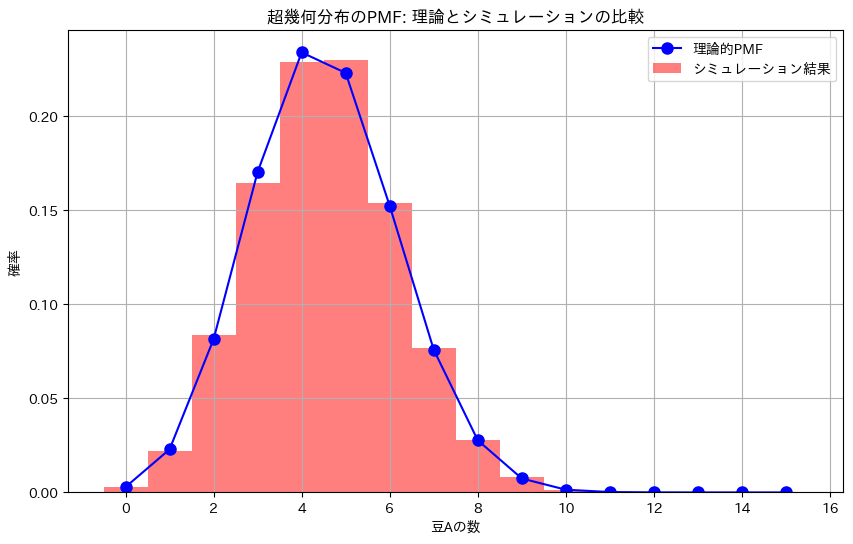
2021 Q1(4)
独立ではない2つの確率変数の積の期待値を求めました。

コード
数式を使った計算
# 2021 Q1(4) 2024.8.20
import sympy as sp
# シンボリック変数の定義
x, y = sp.symbols('x y')
# h(x) の導出
h_x = sp.integrate(sp.exp(-x), (x, 0, x))
# XY の期待値の計算
# h(x) = 1 - exp(-x) を使って E[X * h(X)] を計算する
integral_part1 = sp.integrate(x * h_x * sp.exp(-x), (x, 0, sp.oo))
E_XY_simplified = sp.simplify(integral_part1)
# 結果の表示
display(sp.Eq(sp.Symbol('h(x)'), h_x))
display(sp.Eq(sp.Symbol('E[XY]'), E_XY_simplified))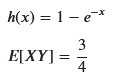
指数分布に従う乱数Xを生成し、Y=h(X)Yが一様分布に従うか確認
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
num_samples = 100000 # サンプル数
# 指数分布に従う乱数 X を生成
X_samples = np.random.exponential(scale=1.0, size=num_samples)
# 関数 Y = h(X) = 1 - exp(-X) を適用して Y を計算
Y_samples = 1 - np.exp(-X_samples)
# ヒストグラムのプロット
plt.figure(figsize=(8, 5))
plt.hist(Y_samples, bins=50, density=True, alpha=0.6, color='g', label='シミュレーションされた Y=h(X)')
plt.xlabel('y')
plt.ylabel('密度')
plt.title('Y = h(X) の分布 (シミュレーション結果)')
plt.legend()
plt.grid(True)
plt.show()
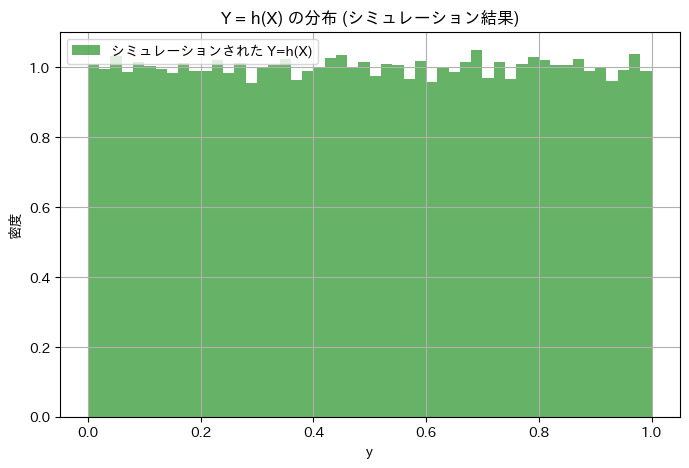
シミュレーションによるE[XY]の計算
import numpy as np
# シミュレーションの設定
num_samples = 100000 # サンプル数
# 指数分布に従う乱数 X を生成
X_samples = np.random.exponential(scale=1.0, size=num_samples)
# 関数 Y = h(X) = 1 - exp(-X) を適用して Y を計算
Y_samples = 1 - np.exp(-X_samples)
# XY の期待値を計算
XY_samples = X_samples * Y_samples
E_XY_simulation = np.mean(XY_samples)
# 結果の表示
print(f"シミュレーションによる E[XY] = {E_XY_simulation}")
print(f"理論値 E[XY] = 3/4 = {3/4}")シミュレーションによる E[XY] = 0.7473462073557277
理論値 E[XY] = 3/4 = 0.75