ホーム » コードあり (ページ 10)
「コードあり」カテゴリーアーカイブ
2018 Q4(3)
マルコフ連鎖する条件付き正規分布の任意のtに対する分布の証明をやりました。

コード
![]() の条件付き分布が
の条件付き分布が![]() に従うのかシミュレーションをしてみます。
に従うのかシミュレーションをしてみます。
# 2018 Q4(3) 2024.10.20
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
t_max = 50 # 時間 t の最大値
n_simulations = 10000 # シミュレーション回数
rho = 0.7 # ρの値
x_0 = 1.0 # X_0 の初期値
# シミュレーション結果を格納するリスト
X_t_samples = np.zeros((t_max, n_simulations))
X_t_samples[0, :] = x_0 # X_0 = x_0
# マルコフプロセスをシミュレーション
for t in range(1, t_max):
# X_t を次のステップで生成
mean = rho**2 * X_t_samples[t-1, :]
variance = 1 - rho**4
X_t_samples[t, :] = np.random.normal(loc=mean, scale=np.sqrt(variance), size=n_simulations)
# シミュレーション結果の平均と分散を計算
simulated_means = np.mean(X_t_samples, axis=1)
simulated_variances = np.var(X_t_samples, axis=1)
# 理論値の期待値と分散を計算
theoretical_means = rho**(2 * np.arange(t_max)) * x_0
theoretical_variances = 1 - rho**(4 * np.arange(t_max))
# グラフを描画
plt.figure(figsize=(10, 6))
# 期待値のプロット
plt.subplot(2, 1, 1)
plt.plot(np.arange(t_max), simulated_means, label="シミュレーション期待値", color='blue', linestyle='--')
plt.plot(np.arange(t_max), theoretical_means, label="理論期待値", color='red')
plt.title("期待値の推移")
plt.xlabel("時間 t")
plt.ylabel("期待値 E[X_t]")
plt.legend()
plt.grid(True)
# 分散のプロット
plt.subplot(2, 1, 2)
plt.plot(np.arange(t_max), simulated_variances, label="シミュレーション分散", color='blue', linestyle='--')
plt.plot(np.arange(t_max), theoretical_variances, label="理論分散", color='red')
plt.title("分散の推移")
plt.xlabel("時間 t")
plt.ylabel("分散 Var[X_t]")
plt.legend()
plt.grid(True)
# グラフを表示
plt.tight_layout()
plt.show()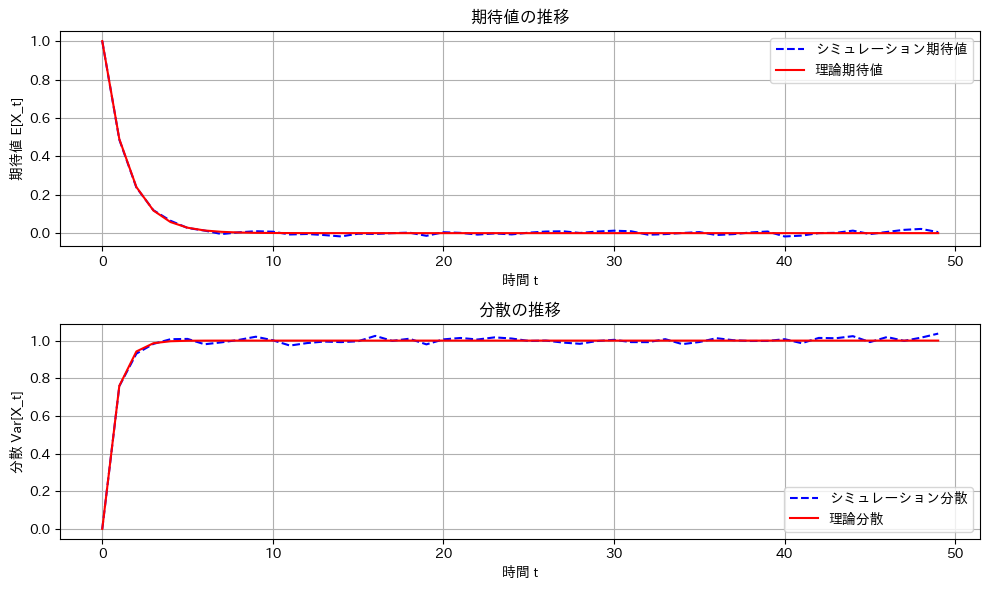
シミュレーションと理論値は一致しました。
2018 Q4(2)-2
マルコフ連鎖する条件付き正規分布の分散の問題をやりました。
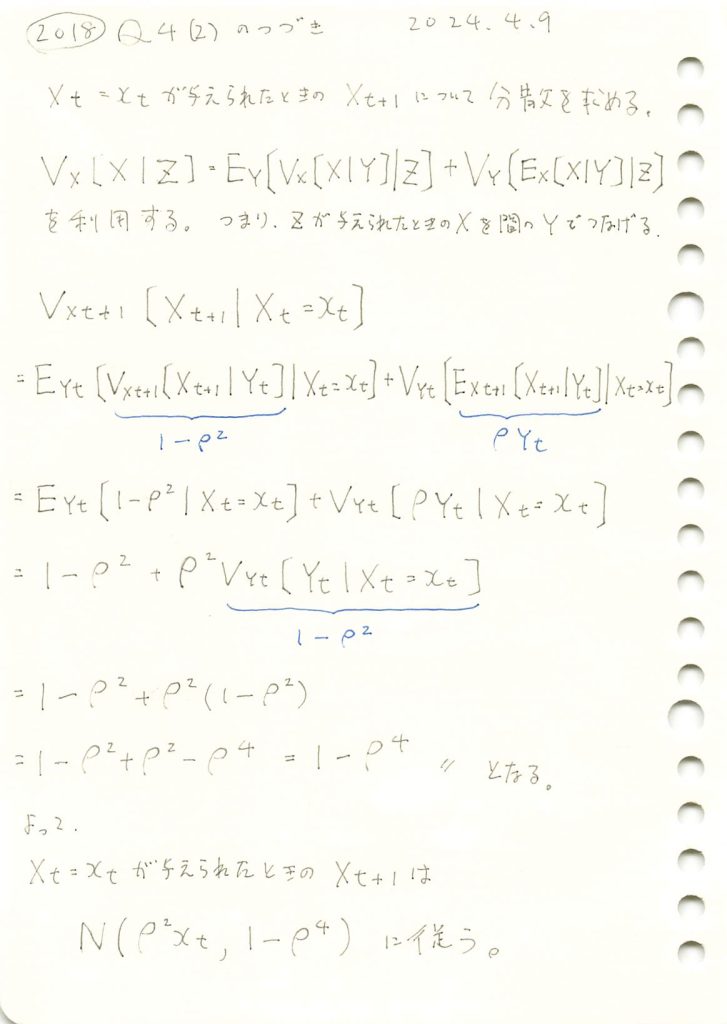
コード
![]() をシミュレーションしてみます。
をシミュレーションしてみます。
#2018 Q4(2) 2024.10.19
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n_simulations = 100000 # シミュレーション回数
rho = 0.7 # ρの値
x_t = 1.0 # X_t の初期値
# シミュレーション結果を格納するリスト
X_t1_samples = []
for _ in range(n_simulations):
# 1. X_t -> Y_t のステップ
y_t = np.random.normal(loc=rho * x_t, scale=np.sqrt(1 - rho**2))
# 2. Y_t -> X_{t+1} のステップ
x_t1 = np.random.normal(loc=rho * y_t, scale=np.sqrt(1 - rho**2))
# 結果をリストに追加
X_t1_samples.append(x_t1)
# シミュレーション結果を配列に変換
X_t1_samples = np.array(X_t1_samples)
# シミュレーション結果の期待値と分散を計算
simulated_mean = np.mean(X_t1_samples)
simulated_variance = np.var(X_t1_samples)
# 理論値の期待値と分散
expected_mean = rho**2 * x_t # 理論上の期待値
expected_variance = 1 - rho**4 # 理論上の分散
# 結果の表示
print(f"理論上の期待値: {expected_mean}, シミュレーションによる期待値: {simulated_mean}")
print(f"理論上の分散: {expected_variance}, シミュレーションによる分散: {simulated_variance}")
# ヒストグラムの表示
plt.hist(X_t1_samples, bins=50, density=True, alpha=0.6, color='g', edgecolor='black', label='シミュレーション')
plt.axvline(expected_mean, color='r', linestyle='--', label=f'理論上の期待値: {expected_mean:.3f}')
plt.title(r"$X_{t+1}$ のシミュレーション (マルコフ性)")
plt.xlabel(r"$X_{t+1}$ の値")
plt.ylabel("頻度")
plt.legend()
plt.grid(True)
plt.show()理論上の期待値: 0.48999999999999994, シミュレーションによる期待値: 0.4909842816275996
理論上の分散: 0.7599, シミュレーションによる分散: 0.7608618418358614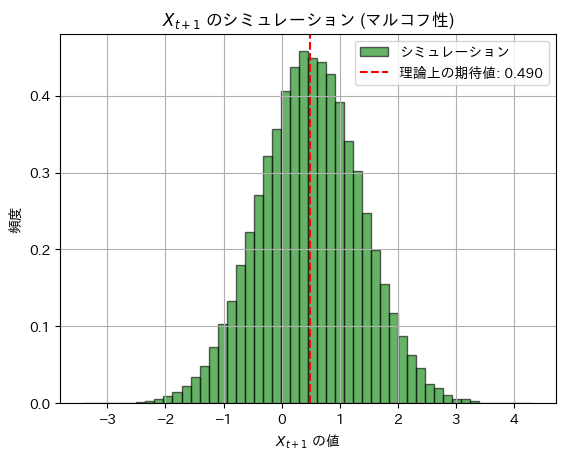
シミュレーション結果は理論値に一致しました。
2018 Q4(2)-1
マルコフ連鎖する条件付き正規分布の期待値の問題をやりました。
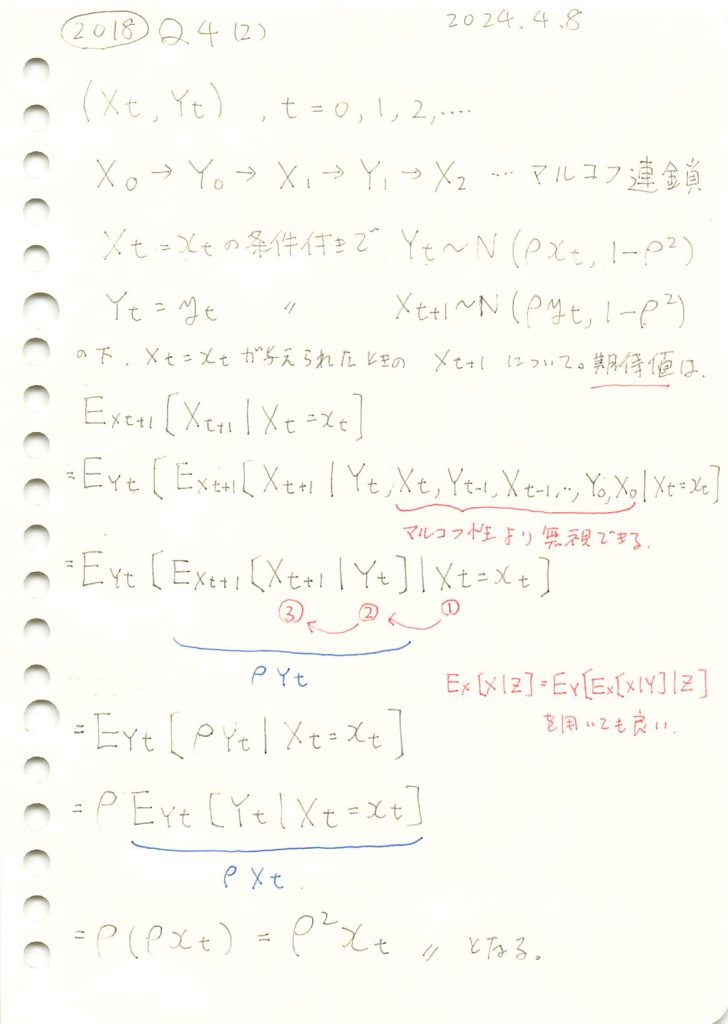
コード
![]() をシミュレーションしてみます。
をシミュレーションしてみます。
#2018 Q4(2) 2024.10.19
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n_simulations = 100000 # シミュレーション回数
rho = 0.7 # ρの値
x_t = 1.0 # X_t の初期値
# シミュレーション結果を格納するリスト
X_t1_samples = []
for _ in range(n_simulations):
# 1. X_t -> Y_t のステップ
y_t = np.random.normal(loc=rho * x_t, scale=np.sqrt(1 - rho**2))
# 2. Y_t -> X_{t+1} のステップ
x_t1 = np.random.normal(loc=rho * y_t, scale=np.sqrt(1 - rho**2))
# 結果をリストに追加
X_t1_samples.append(x_t1)
# シミュレーション結果を配列に変換
X_t1_samples = np.array(X_t1_samples)
# シミュレーション結果の期待値と分散を計算
simulated_mean = np.mean(X_t1_samples)
simulated_variance = np.var(X_t1_samples)
# 理論値の期待値と分散
expected_mean = rho**2 * x_t # 理論上の期待値
expected_variance = 1 - rho**4 # 理論上の分散
# 結果の表示
print(f"理論上の期待値: {expected_mean}, シミュレーションによる期待値: {simulated_mean}")
print(f"理論上の分散: {expected_variance}, シミュレーションによる分散: {simulated_variance}")
# ヒストグラムの表示
plt.hist(X_t1_samples, bins=50, density=True, alpha=0.6, color='g', edgecolor='black', label='シミュレーション')
plt.axvline(expected_mean, color='r', linestyle='--', label=f'理論上の期待値: {expected_mean:.3f}')
plt.title(r"$X_{t+1}$ のシミュレーション (マルコフ性)")
plt.xlabel(r"$X_{t+1}$ の値")
plt.ylabel("頻度")
plt.legend()
plt.grid(True)
plt.show()理論上の期待値: 0.48999999999999994, シミュレーションによる期待値: 0.4909842816275996
理論上の分散: 0.7599, シミュレーションによる分散: 0.7608618418358614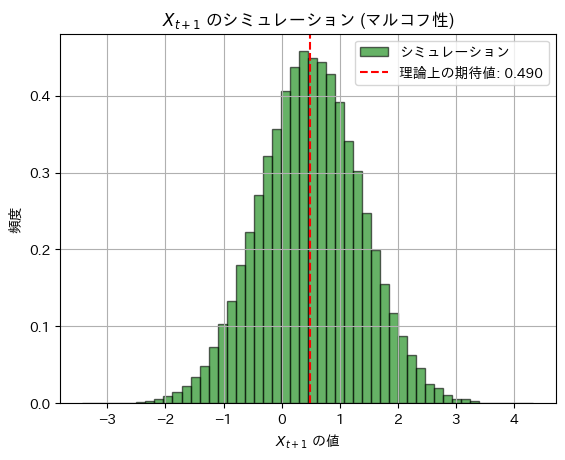
シミュレーション結果は理論値に一致しました。
2018 Q4(1)
条件付きの正規分布の周辺確率密度関数を求めました。

コード
条件付き分布Y|X=x を生成し、Yの周辺分布が標準正規分布に従うかシミュレーションしてみます。
# 2018 Q4(1) 2024.10.18
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# パラメータ設定
rho = 0.7 # 相関係数
# サンプルサイズ
n_samples = 10000
#Xを標準正規分布からサンプル
X = np.random.normal(0, 1, n_samples)
#Y|X=x に基づいてYを生成
Y = np.random.normal(rho * X, np.sqrt(1 - rho**2))
#Yのヒストグラムを描画
plt.hist(Y, bins=50, density=True, alpha=0.6, color='g', label='シミュレーションされた Y')
# 理論的な標準正規分布N(0,1)の曲線を重ねる
x_vals = np.linspace(-4, 4, 1000)
plt.plot(x_vals, norm.pdf(x_vals, 0, 1), 'r-', lw=2, label='理論分布 N(0,1)')
# ラベルを描画
plt.title('シミュレーションされた Y と理論分布 N(0,1) の比較')
plt.xlabel('Y')
plt.ylabel('確率密度')
plt.legend()
# グラフを表示
plt.show()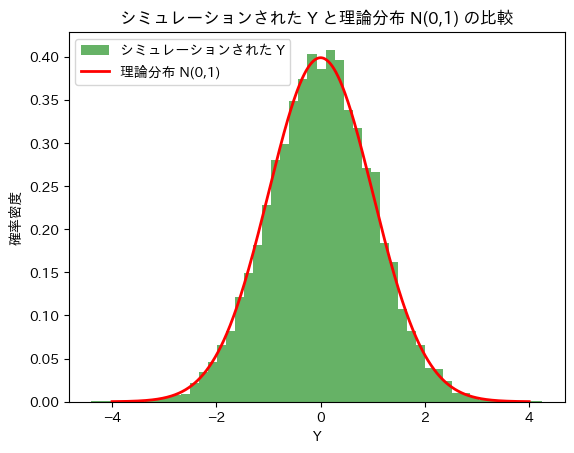
Yは標準正規分布に従うことが確認できました。
2018 Q3(5)
二項分布の条件付き確率質量関数のパラメータの最尤推定の問題をやりました。

コード
![]() として、
として、 ![]() より
より![]() を求めます。まずはfsolveを使用してモーメント法による推定値を求めてみます。
を求めます。まずはfsolveを使用してモーメント法による推定値を求めてみます。
# 2018 Q3(5) 2024.10.17
from scipy.optimize import fsolve
# パラメータ設定
n = 8 # 試行回数
observed_mean = 3.5 # 仮定した標本平均
# モーメント法の方程式
def moment_eq(theta, observed_mean, n):
return observed_mean - (n * theta) / (1 - (1 - theta)**n)
# 数値的に方程式を解く
theta_hat = fsolve(moment_eq, 0.1, args=(observed_mean, n))[0]
# 結果を表示
print(f"θ ハット: {theta_hat}")θ ハット: 0.4328142334547646求まりました。
次に反復計算で解いてみます。
# 2018 Q3(5) 2024.10.17
import numpy as np
# パラメータ設定
n = 8 # 試行回数
observed_mean = 3.5 # 仮定された標本平均
max_iterations = 100 # 最大反復回数
tolerance = 1e-6 # 収束判定の閾値
# 初期推定値
theta_hat = observed_mean / n
# 反復計算
for iteration in range(max_iterations):
new_theta_hat = (observed_mean / n) * (1 - (1 - theta_hat) ** n)
# 収束判定
if abs(new_theta_hat - theta_hat) < tolerance:
break
theta_hat = new_theta_hat
# 結果の表示
print(f"θ ハット: {theta_hat}")θ ハット: 0.432814320144486同じ値になりました。
次は単純にθを0.01から0.99まで変化させて![]() が1になるθを見つけます。
が1になるθを見つけます。
# 2018 Q3(5) 2024.10.17
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 8 # 試行回数
observed_mean = 3.5 # 仮定した標本平均
theta_values = np.linspace(0.01, 0.99, 100) # θを0.01から0.99まで100点で変化させる
# f(θ) の定義
def f_theta(theta, n, observed_mean):
return (n * theta) / (observed_mean * (1 - (1 - theta) ** n))
# f(θ) を計算
f_values = f_theta(theta_values, n, observed_mean)
# f(θ) = 1 となる交点を見つける
intersection_index = np.argmin(np.abs(f_values - 1))
theta_hat = theta_values[intersection_index]
# 交点の θ ハットの値を表示
print(f"θ ハット: {theta_hat}")
# グラフの描画
plt.plot(theta_values, f_values, label='f(θ)', color='blue')
plt.axhline(y=1, color='red', linestyle='--', label='y = 1')
plt.xlabel("θ", fontsize=12)
plt.ylabel("f(θ)", fontsize=12)
plt.title("f(θ) のグラフ (左辺 / 右辺の比)", fontsize=14)
plt.legend()
plt.grid(True)
# グラフの表示
plt.show()θ ハット: 0.43565656565656563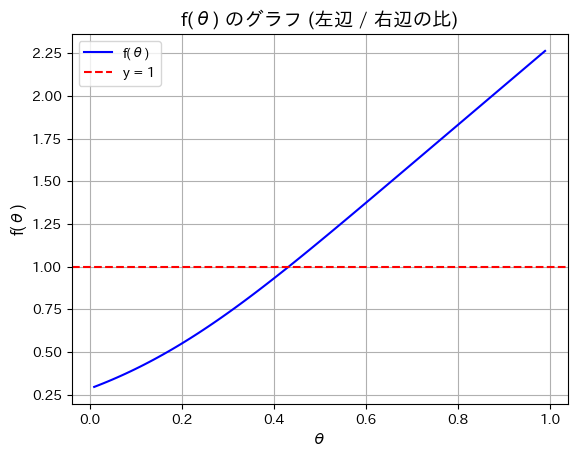
概ね同じ値になりました。
2018 Q3(4)
二項分布の期待値と条件付き期待値との比が2倍になるパラメータを求めました。

コード
n=8に固定しθを変化させて、η(θ)、E[X]、2E[X]の理論値をプロットしてみます。
# 2018 Q3(4) 2024.10.16
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 8 # 試行回数
theta_values = np.linspace(0.01, 0.2, 50) # θを0.01から0.2まで50点で変化
# 条件付き期待値 η(θ) と 条件なしの期待値 E[X] を計算
eta_values = n * theta_values / (1 - (1 - theta_values) ** n) # η(θ)
EX_values = n * theta_values # E[X]
# 二倍のE[X]をプロットするための値
double_EX_values = 2 * EX_values
# グラフの描画
plt.plot(theta_values, eta_values, label='条件付き期待値 η(θ)', color='blue', linestyle='-', marker='o', markersize=4)
plt.plot(theta_values, EX_values, label='条件なし期待値 E[X]', color='green', linestyle='--')
plt.plot(theta_values, double_EX_values, label='2倍の E[X]', color='red', linestyle=':')
# 二倍の関係になるθの位置を求め、プロット
intersection_index = np.argmin(np.abs(eta_values - double_EX_values))
intersection_theta = theta_values[intersection_index]
intersection_eta = eta_values[intersection_index]
plt.scatter(intersection_theta, intersection_eta, color='black', zorder=5, label=f'η(θ) = 2E[X] (θ ≈ {intersection_theta:.3f})')
# キャプションの表示
plt.xlabel("θ", fontsize=12)
plt.ylabel("期待値", fontsize=12)
plt.title("θ に対する η(θ) と E[X] の比較 (理論値)", fontsize=14)
plt.legend()
plt.grid(True)
# グラフの表示
plt.show()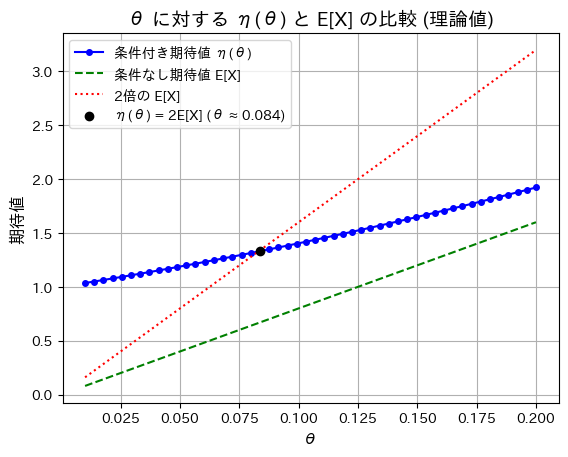
θ=0.083辺りで、η(θ)=2E[X]となることが確認できました。
次に、シミュレーションし同様に描画してみます。
# 2018 Q3(4) 2024.10.16
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 8 # 試行回数
theta_values = np.linspace(0.01, 0.2, 50) # θを0.01から0.2まで50点で変化
num_simulations = 100000 # シミュレーション回数
# シミュレーションによる条件付き期待値 η(θ) と 条件なし期待値 E[X] を計算
eta_values = []
EX_values = []
for theta in theta_values:
# 二項分布のサンプリング
binom_samples = np.random.binomial(n, theta, num_simulations)
# 条件付きサンプル (X >= 1)
samples_X_geq_1 = binom_samples[binom_samples >= 1]
# 条件付き期待値 η(θ)
eta = np.mean(samples_X_geq_1)
eta_values.append(eta)
# 条件なし期待値 E[X]
EX = np.mean(binom_samples)
EX_values.append(EX)
# 2倍のE[X]を計算
double_EX_values = 2 * np.array(EX_values)
# グラフの描画
plt.plot(theta_values, eta_values, label='条件付き期待値 η(θ)', color='blue', linestyle='-', marker='o', markersize=4)
plt.plot(theta_values, EX_values, label='条件なし期待値 E[X]', color='green', linestyle='--')
plt.plot(theta_values, double_EX_values, label='2倍の E[X]', color='red', linestyle=':')
# 二倍の関係になるθの位置を求め、プロット
intersection_index = np.argmin(np.abs(np.array(eta_values) - double_EX_values))
intersection_theta = theta_values[intersection_index]
intersection_eta = eta_values[intersection_index]
plt.scatter(intersection_theta, intersection_eta, color='black', zorder=5, label=f'η(θ) = 2E[X] (θ ≈ {intersection_theta:.3f})')
# キャプションの表示
plt.xlabel("θ", fontsize=12)
plt.ylabel("期待値", fontsize=12)
plt.title("θ に対する η(θ) と E[X] の比較 (シミュレーション)", fontsize=14)
plt.legend()
plt.grid(True)
# グラフの表示
plt.show()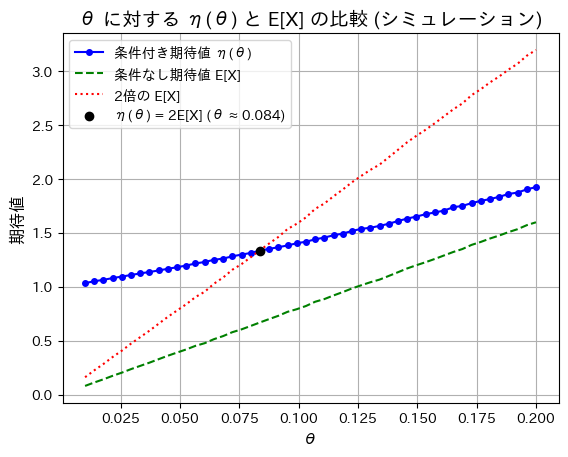
シミュレーションも同じ結果になりました。
2018 Q3(3)
二項分布の条件付き期待値と分散を求めました。

コード
条件付きと条件がついていない場合でシミュレーションし期待値と分散がどのように異なるのか確認します。まずn=10とします。
# 2018 Q3(3) 2024.10.15
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 10 # 試行回数
theta = 0.5 # 成功確率
num_simulations = 100000 # シミュレーション回数
# 二項分布のサンプリング
binom_samples = np.random.binomial(n, theta, num_simulations)
# 条件 X >= 1 を満たすサンプルを抽出
samples_X_geq_1 = binom_samples[binom_samples >= 1]
# 条件付き期待値と条件付き分散のシミュレーションによる計算
simulated_mean = np.mean(samples_X_geq_1)
simulated_variance = np.var(samples_X_geq_1)
# 条件なしの期待値と分散のシミュレーションによる計算
unconditional_simulated_mean = np.mean(binom_samples)
unconditional_simulated_variance = np.var(binom_samples)
# 理論値の計算
theoretical_mean = n * theta / (1 - (1 - theta) ** n)
theoretical_variance = (
(n * theta * (1 - theta)) / (1 - (1 - theta) ** n)
- (n ** 2 * theta ** 2 * (1 - theta) ** n) / (1 - (1 - theta) ** n) ** 2
)
# 条件なしの理論期待値と分散
unconditional_theoretical_mean = n * theta
unconditional_theoretical_variance = n * theta * (1 - theta)
# 結果を表示
print(f"シミュレーションによる条件付き期待値: {simulated_mean}")
print(f"理論上の条件付き期待値: {theoretical_mean}")
print(f"シミュレーションによる条件付き分散: {simulated_variance}")
print(f"理論上の条件付き分散: {theoretical_variance}")
print(f"シミュレーションによる条件なし期待値: {unconditional_simulated_mean}")
print(f"理論上の条件なし期待値: {unconditional_theoretical_mean}")
print(f"シミュレーションによる条件なし分散: {unconditional_simulated_variance}")
print(f"理論上の条件なし分散: {unconditional_theoretical_variance}")
# ヒストグラムの描画
plt.hist(samples_X_geq_1, bins=np.arange(1, n + 2) - 0.5, density=True, alpha=0.6, color='blue', edgecolor='black', label='条件付き (X >= 1)')
plt.hist(binom_samples, bins=np.arange(0, n + 2) - 0.5, density=True, alpha=0.4, color='green', edgecolor='black', label='条件なし')
# 理論値を折れ線グラフで表示
x_values = np.arange(0, n + 1)
binom_pmf = np.array([np.math.comb(n, x) * theta**x * (1 - theta)**(n - x) for x in x_values])
conditional_pmf = binom_pmf[1:] / (1 - binom_pmf[0]) # 条件付きのPMF
plt.plot(x_values[1:], conditional_pmf, marker='x', linestyle='-', color='red', label='条件付き理論値')
plt.plot(x_values, binom_pmf, marker='o', linestyle='-', color='purple', label='条件なし理論値')
# グラフの描画
plt.xlabel("X の値", fontsize=12)
plt.ylabel("確率密度", fontsize=12)
plt.title("条件付きと条件なしの二項分布のシミュレーション", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()シミュレーションによる条件付き期待値: 5.00641686604667
理論上の条件付き期待値: 5.004887585532747
シミュレーションによる条件付き分散: 2.4896127535349235
理論上の条件付き分散: 2.4779819766102995
シミュレーションによる条件なし期待値: 5.00106
理論上の条件なし期待値: 5.0
シミュレーションによる条件なし分散: 2.5137388763999997
理論上の条件なし分散: 2.5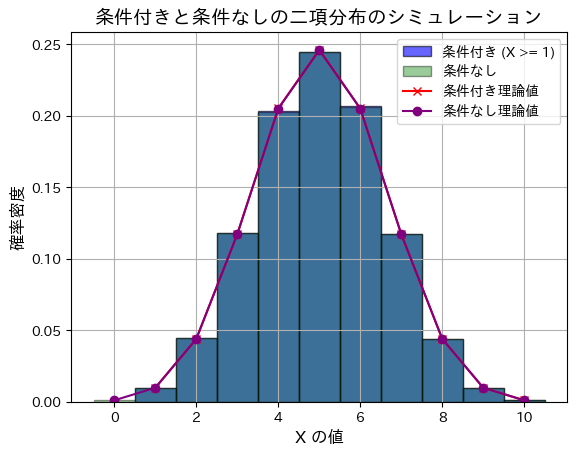
条件付きと条件がついていない場合では、分布はほとんど同じになります。
次に、n=4にすると
シミュレーションによる条件付き期待値: 2.130760208977503
理論上の条件付き期待値: 2.1333333333333333
シミュレーションによる条件付き分散: 0.7789354600394489
理論上の条件付き分散: 0.7822222222222222
シミュレーションによる条件なし期待値: 1.99844
理論上の条件なし期待値: 2.0
シミュレーションによる条件なし分散: 0.9949975664
理論上の条件なし分散: 1.0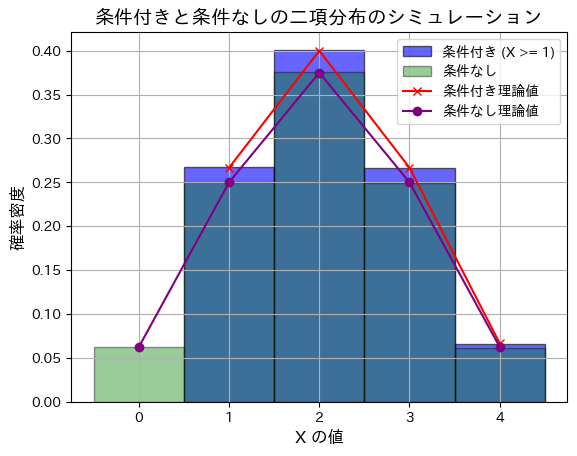
条件付きと条件がついていない場合で、分布の違いが見えてきました。
次に、n=を1から10に変化させて、条件付きと条件がついていない場合の期待値を見てみます。
# 2018 Q3(3) 2024.10.15
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta = 0.5 # 成功確率(固定)
n_values = np.arange(1, 11, 1) # nの値を1から10まで1刻みで変化させる
num_simulations = 100000 # シミュレーション回数
simulated_means = [] # 条件付き期待値のシミュレーション結果
theoretical_means = [] # 条件付き理論期待値
unconditional_means_sim = [] # 条件なしの期待値のシミュレーション結果
unconditional_means_theory = [] # 条件なしの理論期待値
# nを変化させてシミュレーション
for n in n_values:
# 二項分布のサンプリング
binom_samples = np.random.binomial(n, theta, num_simulations)
samples_X_geq_1 = binom_samples[binom_samples >= 1] # X >= 1 の条件に絞る
# シミュレーションによる条件付き期待値
simulated_mean = np.mean(samples_X_geq_1)
simulated_means.append(simulated_mean)
# 条件付き理論期待値
theoretical_mean = n * theta / (1 - (1 - theta) ** n)
theoretical_means.append(theoretical_mean)
# 条件なしの期待値のシミュレーション結果
unconditional_mean_sim = np.mean(binom_samples)
unconditional_means_sim.append(unconditional_mean_sim)
# 条件なしの理論期待値
unconditional_mean_theory = n * theta
unconditional_means_theory.append(unconditional_mean_theory)
# シミュレーション結果と理論値をプロット
plt.plot(n_values, simulated_means, label="条件付きシミュレーション", marker='o', linestyle='--', color='blue')
plt.plot(n_values, theoretical_means, label="条件付き理論値", marker='x', linestyle='-', color='red')
plt.plot(n_values, unconditional_means_sim, label="条件なしシミュレーション", marker='^', linestyle='--', color='purple')
plt.plot(n_values, unconditional_means_theory, label="条件なし理論値", marker='s', linestyle='-', color='green')
# グラフの描画
plt.xlabel("試行回数 n", fontsize=12)
plt.ylabel("期待値 E[X]", fontsize=12)
plt.title("n の変化に対する期待値の比較 (θ = 0.5)", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()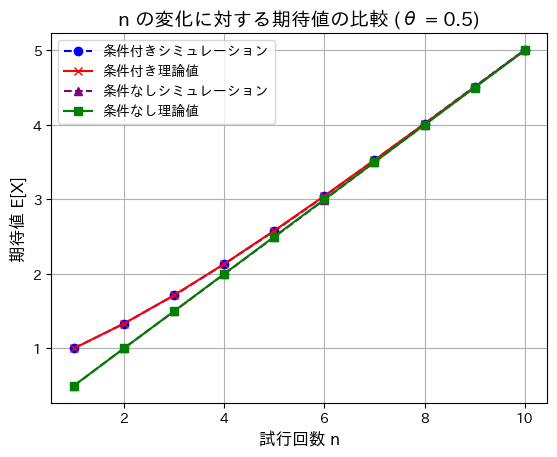
nが増加するほど、条件付きと条件がついていない場合の期待値の差は小さくなります。
分散も同様に確認します。
# 2018 Q3(3) 2024.10.15
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta = 0.5 # 成功確率(固定)
n_values = np.arange(1, 11, 1) # nの値を1から10まで1刻みで変化させる
num_simulations = 100000 # シミュレーション回数
simulated_variances = [] # 条件付き分散のシミュレーション結果
theoretical_variances = [] # 条件付き理論分散
unconditional_variances_sim = [] # 条件なしの分散のシミュレーション結果
unconditional_variances_theory = [] # 条件なしの理論分散
# nを変化させてシミュレーション
for n in n_values:
# 二項分布のサンプリング
binom_samples = np.random.binomial(n, theta, num_simulations)
samples_X_geq_1 = binom_samples[binom_samples >= 1] # X >= 1 の条件に絞る
# シミュレーションによる条件付き分散
simulated_variance = np.var(samples_X_geq_1)
simulated_variances.append(simulated_variance)
# 条件付き理論分散
theoretical_variance = (
(n * theta * (1 - theta)) / (1 - (1 - theta) ** n)
- (n ** 2 * theta ** 2 * (1 - theta) ** n) / (1 - (1 - theta) ** n) ** 2
)
theoretical_variances.append(theoretical_variance)
# 条件なしの分散のシミュレーション結果
unconditional_variance_sim = np.var(binom_samples)
unconditional_variances_sim.append(unconditional_variance_sim)
# 条件なしの理論分散
unconditional_variance_theory = n * theta * (1 - theta)
unconditional_variances_theory.append(unconditional_variance_theory)
# シミュレーション結果と理論値をプロット
plt.plot(n_values, simulated_variances, label="条件付きシミュレーション", marker='o', linestyle='--', color='blue')
plt.plot(n_values, theoretical_variances, label="条件付き理論値", marker='x', linestyle='-', color='red')
plt.plot(n_values, unconditional_variances_sim, label="条件なしシミュレーション", marker='^', linestyle='--', color='purple')
plt.plot(n_values, unconditional_variances_theory, label="条件なし理論値", marker='s', linestyle='-', color='green')
# グラフの描画
plt.xlabel("試行回数 n", fontsize=12)
plt.ylabel("分散 V[X]", fontsize=12)
plt.title("n の変化に対する分散の比較 (θ = 0.5)", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()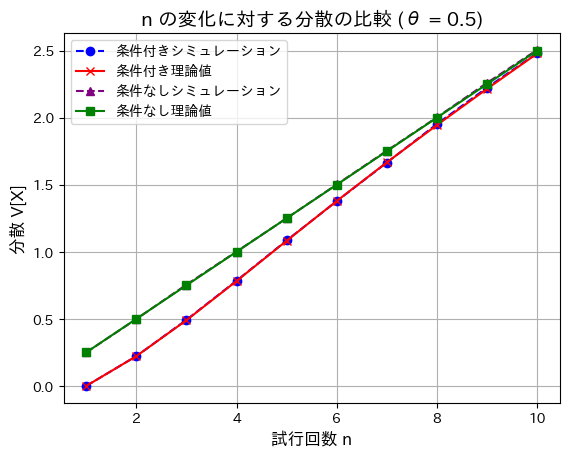
分散も同様に、nが増加するほど差は小さくなりました。
2018 Q3(2)
二項分布の条件付き確率質量関数を求めました。

コード
条件付き二項分布のシミュレーションを行い理論値と一致するか確認します。
# 2018 Q3(2) 2024.10.12
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
n = 10 # 試行回数
theta = 0.5 # 成功確率
num_simulations = 10000 # シミュレーション回数
# 二項分布に従うランダム変数を生成
binom_samples = np.random.binomial(n, theta, num_simulations)
# X >= 1 の条件を満たすサンプルを抽出
samples_X_geq_1 = binom_samples[binom_samples >= 1]
# X = x の回数を数える
counts, _ = np.histogram(samples_X_geq_1, bins=np.arange(n+2))
# シミュレーションによる条件付き確率(X = 1 から n の範囲で計算)
simulated_probabilities = counts[1:] / np.sum(counts)
# 理論上の条件付き確率 h(x)
x_values = np.arange(1, n+1)
binom_pmf = np.array([np.math.comb(n, x) * theta**x * (1-theta)**(n-x) for x in x_values])
theoretical_probabilities = binom_pmf / (1 - (1 - theta)**n)
# シミュレーション結果をヒストグラムで表示
plt.bar(x_values, simulated_probabilities, color='blue', alpha=0.6, label="シミュレーション")
plt.plot(x_values, theoretical_probabilities, label="理論値", marker='x', linestyle='-', color='red')
# グラフの描画
plt.xlabel("X の値", fontsize=12)
plt.ylabel("条件付き確率 P(X = x | X >= 1)", fontsize=12)
plt.title(f"条件付き確率のシミュレーションと理論値の比較 (n={n}, θ={theta})", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()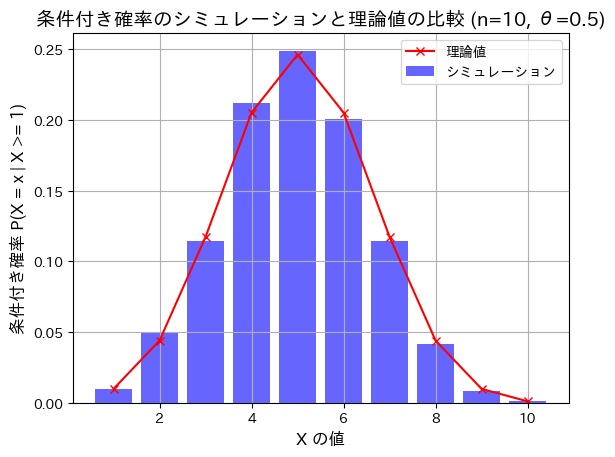
シミュレーションによる結果と理論値が一致しました。
2018 Q3(1)
二項分布の期待値と分散を求めました。
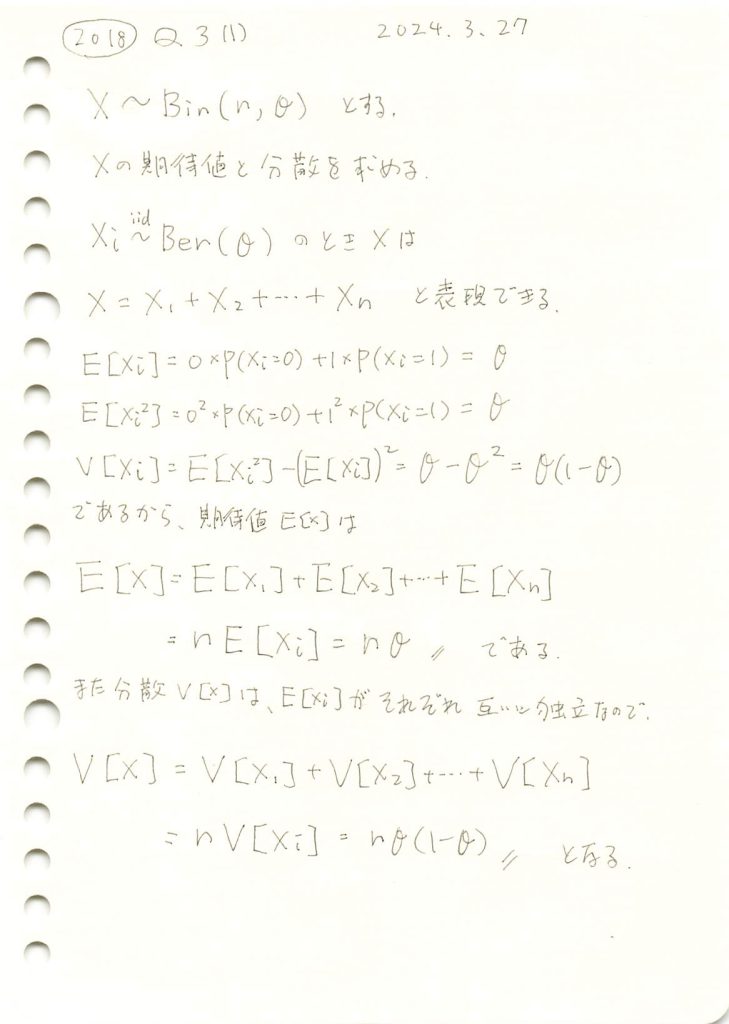
コード
ベルヌーイ試行による二項分布のシミュレーションを行い二項分布の期待値と分散を求めます。
# 2018 Q3(1) 2024.10.11
import numpy as np
import matplotlib.pyplot as plt
# パラメータ
n = 10 # 試行回数
theta = 0.5 # 成功確率
num_simulations = 10000 # シミュレーションの回数
# シミュレーションを実行
bernoulli_trials = np.random.binomial(1, theta, (num_simulations, n))
# 各シミュレーションでの X = X1 + X2 + ... + Xn を計算
X_values = np.sum(bernoulli_trials, axis=1)
# 期待値と分散を計算
simulated_mean = np.mean(X_values)
simulated_variance = np.var(X_values)
# 理論値
theoretical_mean = n * theta
theoretical_variance = n * theta * (1 - theta)
# 結果を表示
print(f"シミュレーションによる期待値: {simulated_mean}")
print(f"理論上の期待値: {theoretical_mean}")
print(f"シミュレーションによる分散: {simulated_variance}")
print(f"理論上の分散: {theoretical_variance}")
# ヒストグラムを描画
plt.hist(X_values, bins=np.arange(n+2)-0.5, density=True, alpha=0.75, color='blue', edgecolor='black')
plt.title("ベルヌーイ試行による二項分布のシミュレーション")
plt.xlabel("Xの値 (成功回数)")
plt.ylabel("確率")
plt.show()シミュレーションによる期待値: 4.9827
理論上の期待値: 5.0
シミュレーションによる分散: 2.54300071
理論上の分散: 2.5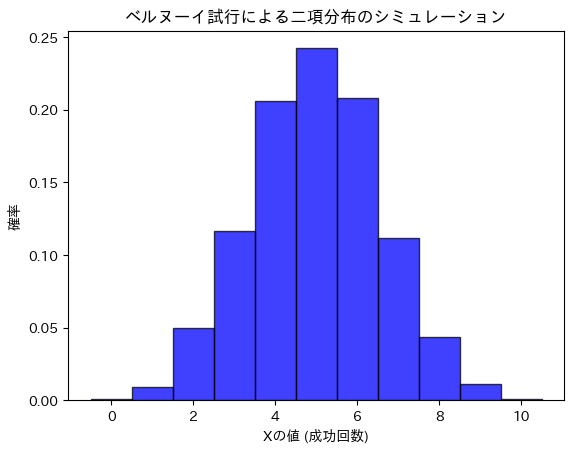
シミュレーションによる結果と理論値が一致しました。
2018 Q2(5)-2
漸近分散の相対標準偏差を求める問題をやりました。

コード
NとMを変化させてシミュレーションし![]() の分布を描画しました。
の分布を描画しました。![]() を求め、理論値と一致するか確認してみます。
を求め、理論値と一致するか確認してみます。
# 2018 Q2(5)-2 2024.10.10
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
N_true = 1000 # 真の青球の数 N (これを推定する)
K_values = [100, 300, 500] # 赤球の数 K のバリエーション
n_values = [100, 200, 300] # 抽出する回数 n のバリエーション
n_trials = 10000 # シミュレーションの試行回数
# グラフレイアウト設定
fig, axes = plt.subplots(len(K_values), len(n_values), figsize=(15, 12))
axes = axes.flatten()
plot_idx = 0
# 各 K, n の組み合わせに対してシミュレーションを実行
for K in K_values:
for n in n_values:
N_hat_values = []
for _ in range(n_trials):
# 青球 N 個 + 赤球 K 個のボールを作成
balls = [0] * N_true + [1] * K # 0が青球、1が赤球
drawn_balls = np.random.choice(balls, size=n, replace=False) # 非復元抽出
X = np.sum(drawn_balls) # 抽出された赤球の個数
# X を使って N の推定量 N_hat を計算
if X > 0: # Xが0でない場合
N_hat = K * (n - X) / X
N_hat_values.append(N_hat)
# シミュレーション結果から N_hat の分散を計算
N_hat_var = np.var(N_hat_values)
# 理論値 ε の計算
epsilon_theory = np.sqrt((N_true + K) * (N_true + K - n) / (n * N_true * K))
# シミュレーションから求めた ε の計算
epsilon_simulation = np.sqrt(N_hat_var) / N_true
# 推定量 N_hat の分布をヒストグラムで表示
ax = axes[plot_idx]
ax.hist(N_hat_values, bins=100, density=True, alpha=0.7, color='b', edgecolor='black')
ax.axvline(x=N_true, color='r', linestyle='--') # 真の N を破線で表示
ax.set_title(f'K={K}, n={n}')
ax.set_xlabel('推定量 N_hat')
ax.set_ylabel('確率密度')
# εの値と真のNをまとめて表示
ax.text(0.95, 0.95, f'真の N = {N_true}\nε (理論) = {epsilon_theory:.4f}\nε (シミュ) = {epsilon_simulation:.4f}',
transform=ax.transAxes, verticalalignment='top', horizontalalignment='right',
bbox=dict(facecolor='white', alpha=0.7), fontsize=10)
ax.grid(True)
plot_idx += 1
# グラフ全体の調整
plt.tight_layout()
plt.show()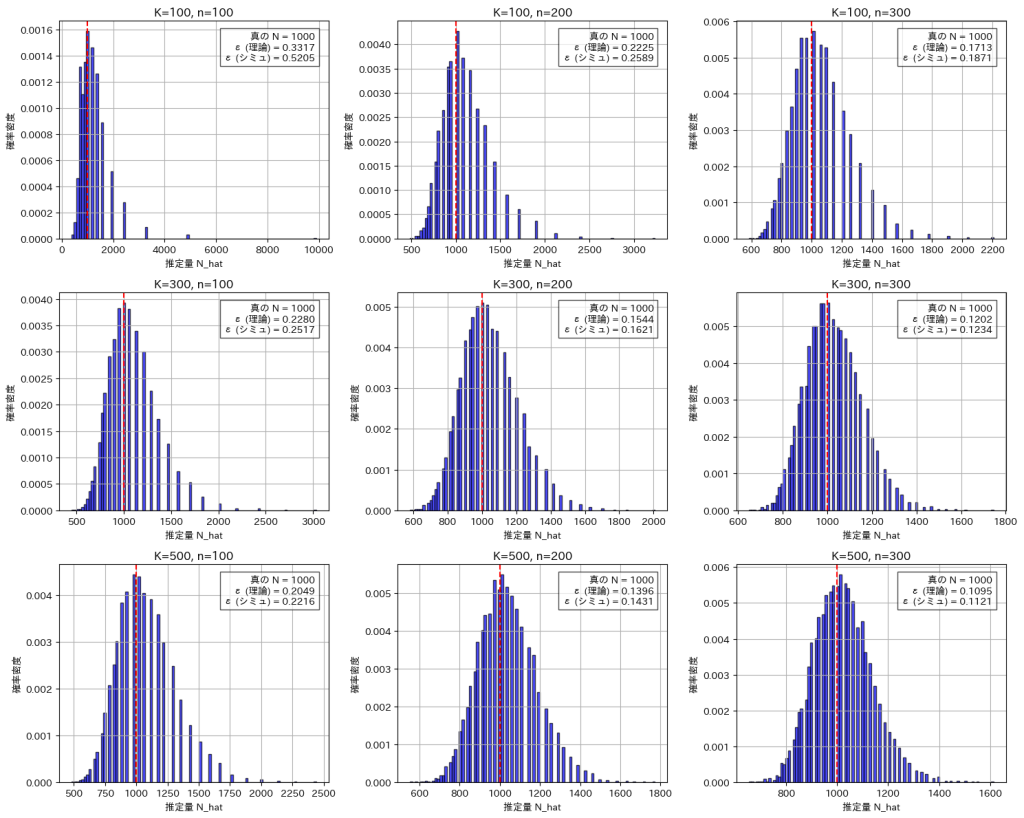
シミュレーションによる結果は理論値と概ね一致しました。