ホーム » チェビシェフの不等式
「チェビシェフの不等式」カテゴリーアーカイブ
2015 Q1(4)
不偏分散が母分散の一致推定量であることを確認しました。

コード
![]() が
が![]() の一致推定量であるか確認するため、
の一致推定量であるか確認するため、![]() をシミュレーションし、理論値とともにグラフで確認してみます。
をシミュレーションし、理論値とともにグラフで確認してみます。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
mu = 0 # 母平均
sigma2 = 4 # 母分散
sigma = np.sqrt(sigma2) # 母標準偏差
n_values = [10, 20, 50, 100, 200] # 標本サイズ
num_simulations = 1000 # シミュレーション回数
# 不偏分散の分散をシミュレーションで計算
simulated_variances = []
theoretical_variances = []
for n in n_values:
sample_variances = []
for _ in range(num_simulations):
sample = np.random.normal(mu, sigma, n)
unbiased_variance = np.var(sample, ddof=1) # 不偏分散
sample_variances.append(unbiased_variance)
# サンプル分散の分散を計算
var_of_sample_variance = np.var(sample_variances)
simulated_variances.append(var_of_sample_variance)
# 理論値を計算
theoretical_variance = 2 * sigma2**2 / (n - 1)
theoretical_variances.append(theoretical_variance)
# グラフの作成
plt.figure(figsize=(10, 6))
plt.plot(n_values, simulated_variances, marker='o', linestyle='-', color='blue', label="シミュレーション値")
plt.plot(n_values, theoretical_variances, marker='o', linestyle='--', color='orange', label="理論値")
# グラフの装飾
plt.title("不偏分散の分散の収束 (シミュレーション vs 理論)")
plt.xlabel("標本サイズ n")
plt.ylabel("分散 (Var[$S^2$])")
plt.grid()
plt.legend()
plt.tight_layout()
plt.show()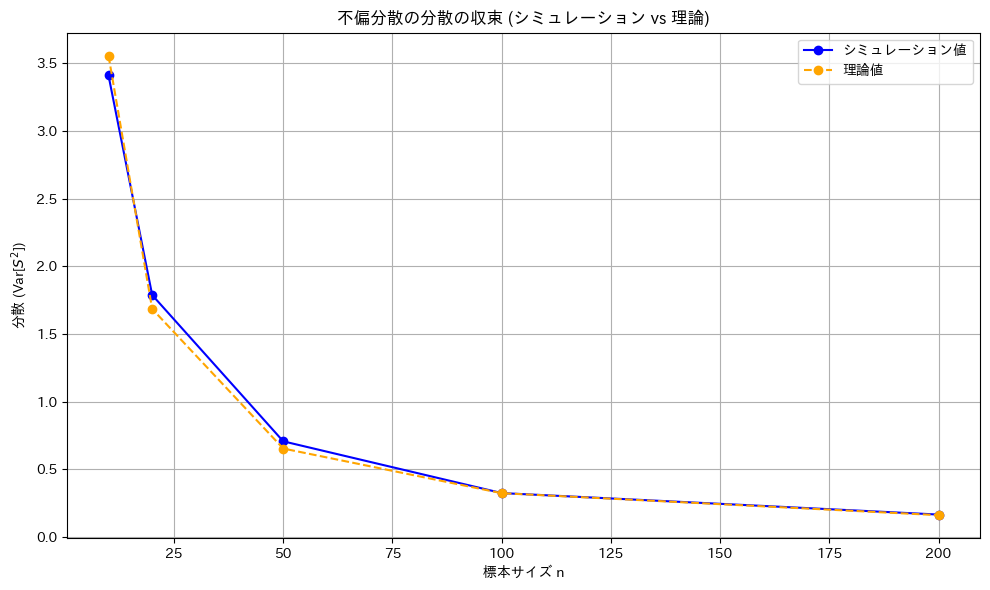
![]() のシミュレーション結果は、理論値
のシミュレーション結果は、理論値![]() とよく一致しました。また、nが増加すると分散が0に近づき、
とよく一致しました。また、nが増加すると分散が0に近づき、![]() が
が![]() の一致推定量であることが確認できました。
の一致推定量であることが確認できました。