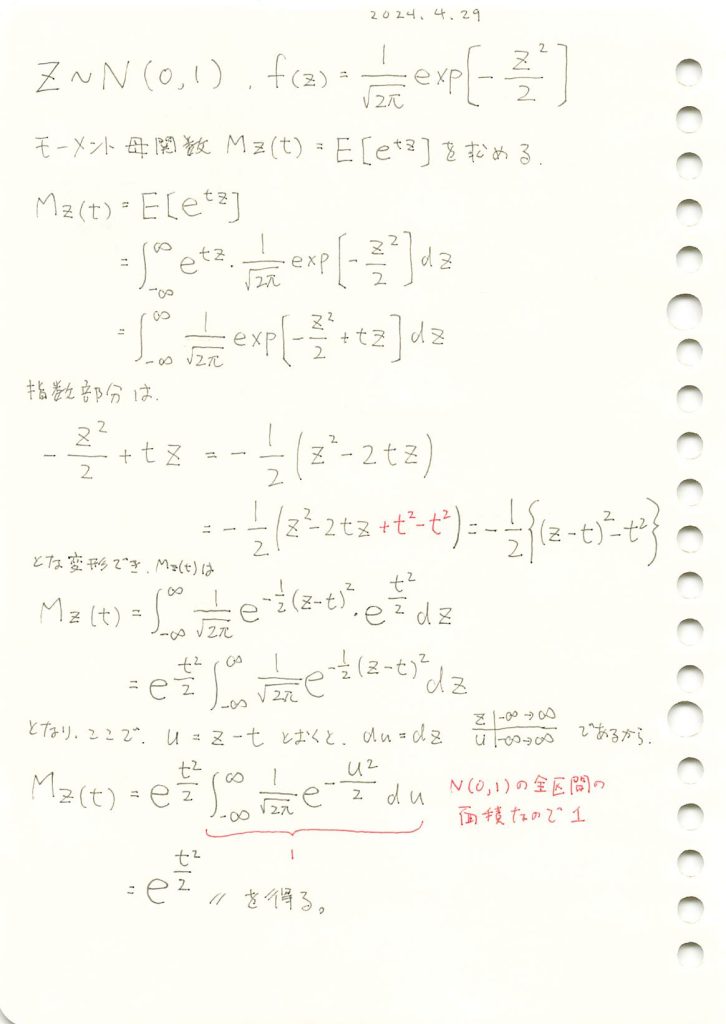2016 Q1(1)
正規分布の母平均μに対してθ=exp(μ)をパラメータとする最尤推定を行いました。
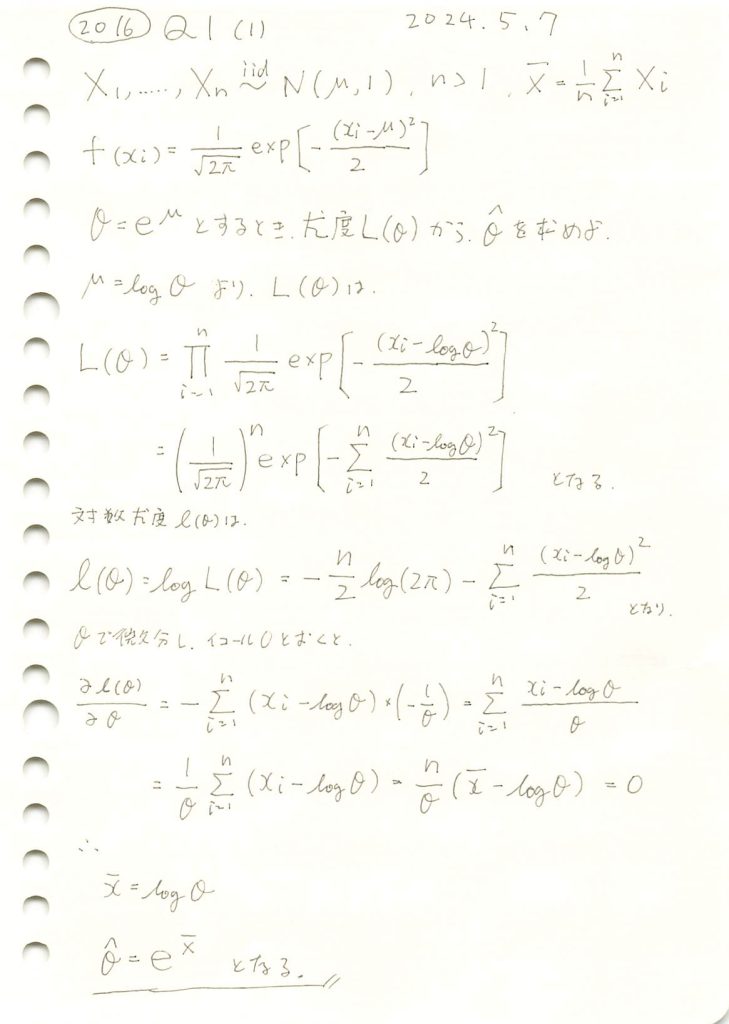
コード
![]() が真のθに近づくか確認するためシミュレーションを行います。まずはサンプルサイズn=5でやってみます。
が真のθに近づくか確認するためシミュレーションを行います。まずはサンプルサイズn=5でやってみます。
# 2016 Q1(1) 2024.11.11
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
mu_true = 1.0 # 真の平均 (mu)
theta_true = np.exp(mu_true) # 真の theta = e^mu
n_samples = 5 # サンプル数
n_trials = 100000 # シミュレーション試行回数
# 乱数生成と最尤推定量の計算
theta_estimates = []
for _ in range(n_trials):
sample = np.random.normal(loc=mu_true, scale=1, size=n_samples) # 正規分布からサンプルを生成
mu_hat = np.mean(sample) # 平均値を計算 (muの最尤推定量)
theta_hat = np.exp(mu_hat) # theta = e^mu の推定値
theta_estimates.append(theta_hat)
# 真の値とシミュレーションの平均を計算
theta_hat_mean = np.mean(theta_estimates)
# 真の値と推定量の平均値を表示
print(f"真の θ: {theta_true:.4f}")
print(f"θハットの平均値 (シミュレーション): {theta_hat_mean:.4f}")
# グラフの描画
plt.hist(theta_estimates, bins=100, density=True, alpha=0.6, color='blue', label='シミュレーションによる$\hat{\\theta}$')
plt.axvline(theta_true, color='red', linestyle='dashed', linewidth=2, label=f'真の$\\theta$: {theta_true:.2f}')
plt.axvline(theta_hat_mean, color='green', linestyle='dashed', linewidth=2, label=f'$\\hat{{\\theta}}$平均: {theta_hat_mean:.2f}')
plt.title('$\\hat{\\theta}$の分布(最尤推定量)')
plt.xlabel('$\\theta$')
plt.ylabel('密度')
plt.legend()
plt.grid(True)
plt.show()
真の θ: 2.7183
θハットの平均値 (シミュレーション): 3.0120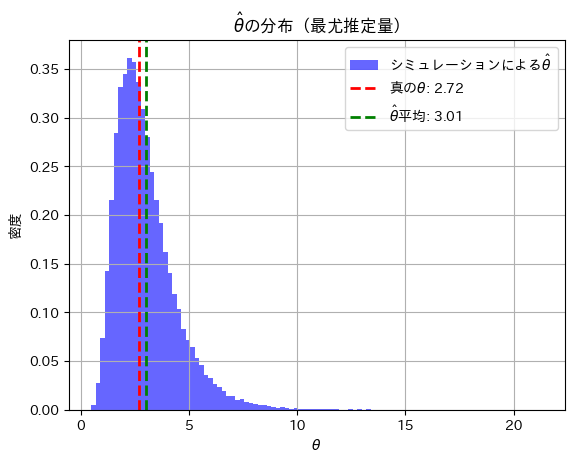
![]() と真のθの間に少し乖離が見られます。サンプルサイズnが小さいことが起因しているかもしれません。
と真のθの間に少し乖離が見られます。サンプルサイズnが小さいことが起因しているかもしれません。
次に、サンプルサイズn=5, 10, 20, 50と変化させて、この乖離がどのように変わるかを確認してみます。
# 2016 Q1(1) 2024.11.11
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションのパラメータ
mu_true = 1.0 # 真の平均 (mu)
theta_true = np.exp(mu_true) # 真の theta = e^mu
n_trials = 100000 # シミュレーション試行回数
sample_sizes = [5, 10, 20, 50] # サンプルサイズのリスト
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.ravel() # 2x2 の配列を平坦化
for i, n_samples in enumerate(sample_sizes):
theta_estimates = []
for _ in range(n_trials):
sample = np.random.normal(loc=mu_true, scale=1, size=n_samples)
mu_hat = np.mean(sample)
theta_hat = np.exp(mu_hat)
theta_estimates.append(theta_hat)
theta_hat_mean = np.mean(theta_estimates)
# ヒストグラムのプロット
axes[i].hist(theta_estimates, bins=100, density=True, alpha=0.6, color='blue', label='シミュレーションによる$\hat{\\theta}$')
axes[i].axvline(theta_true, color='red', linestyle='dashed', linewidth=2, label=f'真の$\\theta$: {theta_true:.2f}')
axes[i].axvline(theta_hat_mean, color='green', linestyle='dashed', linewidth=2, label=f'$\\hat{{\\theta}}$平均: {theta_hat_mean:.2f}')
axes[i].set_title(f'サンプルサイズ n={n_samples}')
axes[i].set_xlabel('$\\theta$')
axes[i].set_ylabel('密度')
axes[i].legend()
axes[i].grid(True)
plt.suptitle('$\\hat{\\theta}$の分布(最尤推定量)', fontsize=16)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()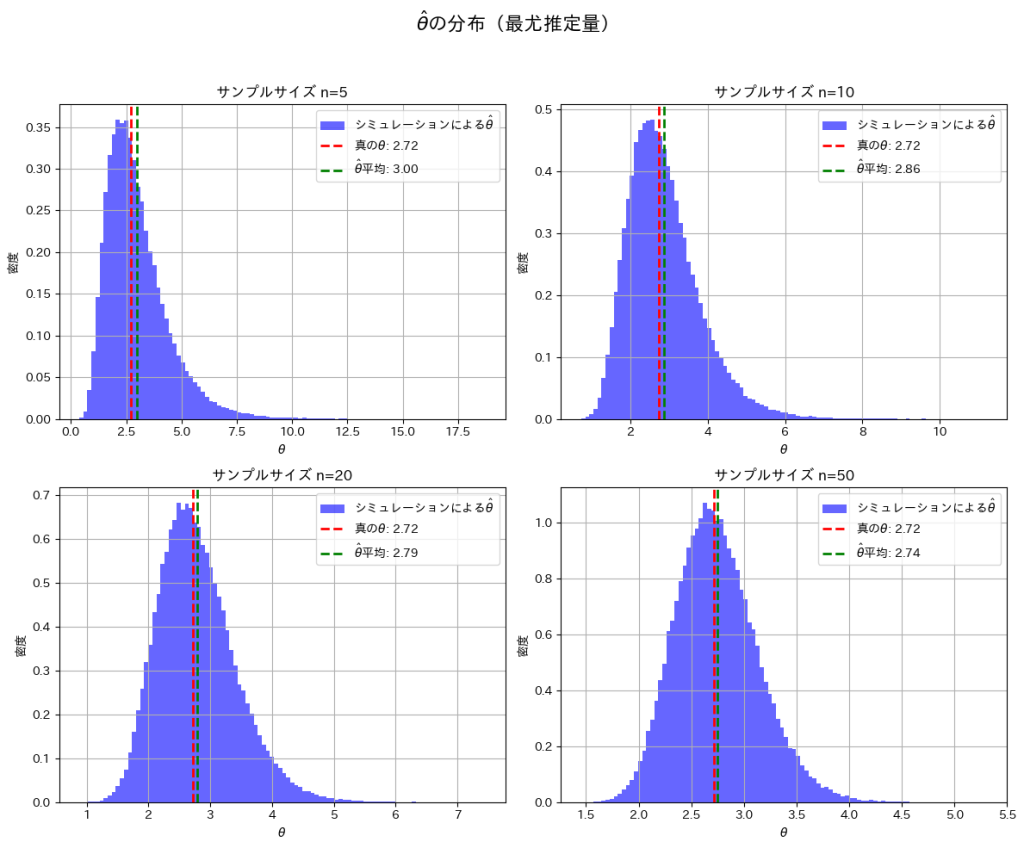
nを大きくすることで、![]() と真のθの間の乖離が小さくなることを確認できました。
と真のθの間の乖離が小さくなることを確認できました。
2017 Q5(3)
独立した二つの自由度1のカイ二乗分布の差を幾何平均と2でスケールした式の確率密度関数を導出しました。

コード
Tについてシミュレーションし、確率密度関数![]() と一致するか確認をします。
と一致するか確認をします。
# 2017 Q5(3) 2024.11.10
import numpy as np
import matplotlib.pyplot as plt
# サンプルサイズ
n_samples = 100000
# 自由度1のカイ二乗分布からサンプルを生成
X = np.random.chisquare(df=1, size=n_samples)
Y = np.random.chisquare(df=1, size=n_samples)
# 確率変数 T = (X - Y) / (2 * sqrt(X * Y)) の計算
T = (X - Y) / (2 * np.sqrt(X * Y))
# 理論的な確率密度関数 h(t) の定義
def theoretical_h(t):
return 1 / (np.pi * (1 + t**2))
# x 軸の範囲を設定し、h(t) を計算
x = np.linspace(-10, 10, 100)
h_t = theoretical_h(x)
# グラフの描画
plt.hist(T, bins=200, density=True, alpha=0.5, range=(-10, 10), label='シミュレーションによる $T$')
plt.plot(x, h_t, 'r-', label='理論的な $h(t) = \\frac{1}{\\pi(1+t^2)}$')
plt.xlabel('$T$')
plt.ylabel('密度')
plt.legend()
plt.title('確率変数 $T$ のシミュレーションと理論密度関数')
plt.show()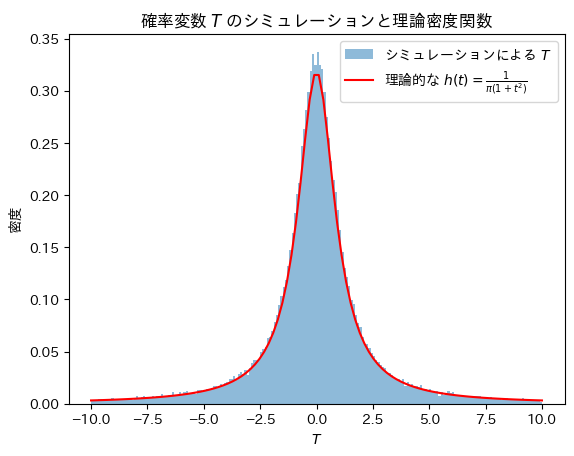
Tの分布は確率密度関数![]() と一致することが確認できました。
と一致することが確認できました。
なお、Tの分布は標準コーシー分布と呼ばれます。
2017 Q5(2)
独立した二つの自由度1のカイ二乗分布の比の確率密度関数を導出し、F(1,1)分布と同じであることを確認しました。

コード
Sについてシミュレーションし、確率密度関数![]() と一致するか確認をします。
と一致するか確認をします。
# 2017 Q5(2) 2024.11.9
import numpy as np
import matplotlib.pyplot as plt
# サンプルサイズ
n_samples = 100000
# 自由度1のカイ二乗分布からサンプルを生成
X = np.random.chisquare(df=1, size=n_samples)
Y = np.random.chisquare(df=1, size=n_samples)
# 確率変数 S = X / Y の計算
S = X / Y
# 理論的な確率密度関数 g(s) の定義
def theoretical_g(s):
return (1 / (np.pi * np.sqrt(s) * (1 + s)))
# x 軸の範囲を設定し、g(s) を計算
x = np.linspace(0.01, 10, 100) # 0.01から10の範囲に制限
g_s = theoretical_g(x)
# ヒストグラムの描画
plt.hist(S, bins=200, density=True, alpha=0.5, range=(0, 10), label='シミュレーションによる $S=X/Y$')
plt.plot(x, g_s, 'r-', label='理論的な $g(s) = \\frac{1}{\\pi \\sqrt{s}} \\cdot \\frac{1}{1+s}$')
plt.xlabel('$S$')
plt.ylabel('密度')
plt.legend()
plt.title('確率変数 $S=X/Y$ のシミュレーションと理論密度関数')
plt.show()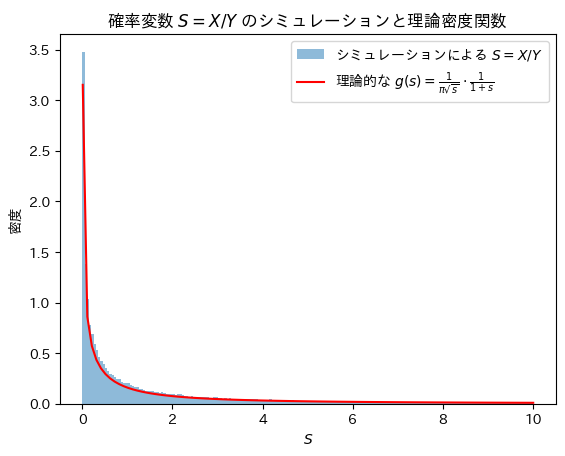
Sの分布は確率密度関数![]() と一致することが確認できました。
と一致することが確認できました。
2017 Q5(1)
標準正規分布から自由度1のカイ二乗分布の確率密度関数を導出しました。
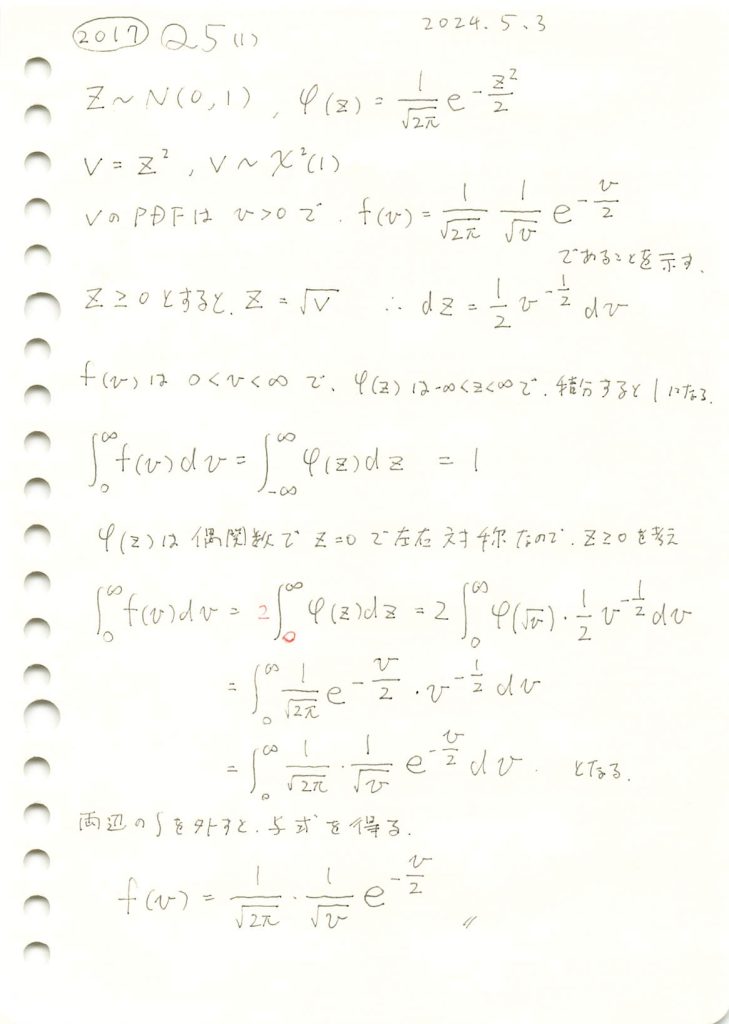
コード
Vについてシミュレーションし、確率密度関数![]() と一致するか確認をします。
と一致するか確認をします。
# 2017 Q5(1) 2024.11.8
import numpy as np
import matplotlib.pyplot as plt
# サンプルサイズ
n_samples = 10000
# 標準正規分布 N(0, 1) からサンプルを生成
Z = np.random.normal(0, 1, n_samples)
# Z を二乗して V を計算
V = Z**2
# 導いた理論的な確率密度関数 f(v) の定義
def theoretical_pdf(v):
return (1 / np.sqrt(2 * np.pi)) * (1 / np.sqrt(v)) * np.exp(-v / 2)
# x 軸の範囲を設定し、f(v) を計算
x = np.linspace(0.01, 10, 100) # 0に近い値での計算エラーを避けるため0.01から
f_v = theoretical_pdf(x)
# ヒストグラムの描画
plt.hist(V, bins=200, density=True, alpha=0.5, label='シミュレーションによる $V=Z^2$')
plt.plot(x, f_v, 'r-', label='理論的な $f(v) = \\frac{1}{\\sqrt{2\\pi}} \\cdot \\frac{1}{\\sqrt{v}} e^{-v/2}$')
plt.xlabel('$V$')
plt.ylabel('密度')
plt.legend()
plt.title('自由度1のカイ二乗分布に従う $V=Z^2$ のシミュレーションと理論密度関数')
plt.show()
Vの分布は確率密度関数![]() と一致することが確認できました。
と一致することが確認できました。
2017 Q4(4)
線形関係のある確率変数の条件付き確率分布を求めました。

コード
X|Z=zが![]() に従うかシミュレーションし確かめます。
に従うかシミュレーションし確かめます。
# 2017 Q4(4) 2024.11.7
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 定数の設定
a = 1
k = 2
num_samples = 1000000
z_fixed = 3 # 条件として与える Z の値
# シミュレーション
Y = np.random.normal(0, 1, num_samples)
X = np.random.normal(0, 1, num_samples)
Z = a + k * X + Y
# Z = z_fixed に条件を付けた X の分布を抽出
X_given_Z = (X[np.abs(Z - z_fixed) < 0.05])
# 理論値の計算
mean_conditional = (k / (k**2 + 1)) * (z_fixed - a)
std_dev_conditional = np.sqrt(1 / (k**2 + 1))
# シミュレーションによる値の計算
mean_simulation = np.mean(X_given_Z)
std_dev_simulation = np.std(X_given_Z)
# 理論値とシミュレーション値を出力
print(f"理論上の期待値 (X | Z = {z_fixed}): {mean_conditional}")
print(f"シミュレーションによる期待値: {mean_simulation}")
print(f"理論上の標準偏差: {std_dev_conditional}")
print(f"シミュレーションによる標準偏差: {std_dev_simulation}")
# 条件付き分布のヒストグラム
plt.hist(X_given_Z, bins=50, density=True, alpha=0.6, color='b', label=f"シミュレーション X | Z = {z_fixed}")
# 理論分布をプロット
x_vals = np.linspace(min(X_given_Z), max(X_given_Z), 100)
plt.plot(x_vals, norm.pdf(x_vals, mean_conditional, std_dev_conditional), 'r', label="理論分布")
# グラフの装飾
plt.title(f"条件付き分布 X | Z = {z_fixed}")
plt.xlabel("X の値")
plt.ylabel("密度")
plt.legend()
plt.show()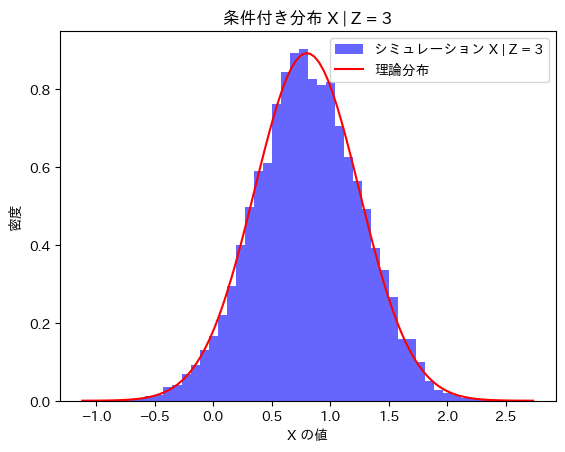
X|Z=zは![]() に従うことが確認できました。
に従うことが確認できました。
2017 Q4(1)(2)(3)
線形関係のある確率変数との相関係数や条件付き確率分布を求めました。

コード
(1) Zが![]() に従うかシミュレーションし確かめます。
に従うかシミュレーションし確かめます。
# 2017 Q4(1) 2024.11.6
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 定数の設定
a = 1
k = 2
num_samples = 10000
# シミュレーション
X = np.random.normal(0, 1, num_samples)
Y = np.random.normal(0, 1, num_samples)
Z = a + k * X + Y
# 理論値の計算
mean_theory = a
std_dev_theory = np.sqrt(k**2 + 1)
# シミュレーションによる値の計算
mean_simulation = np.mean(Z)
std_dev_simulation = np.std(Z)
# 理論値とシミュレーションによる値の表示
print(f"理論上の期待値: {mean_theory}")
print(f"シミュレーションによる期待値: {mean_simulation}")
print(f"理論上の標準偏差: {std_dev_theory}")
print(f"シミュレーションによる標準偏差: {std_dev_simulation}")
# ヒストグラムのプロット
plt.hist(Z, bins=50, density=True, alpha=0.6, color='b', label="シミュレーションによる Z の分布")
# 理論分布のプロット
x_vals = np.linspace(min(Z), max(Z), 100)
plt.plot(x_vals, norm.pdf(x_vals, mean_theory, std_dev_theory), 'r', label="理論分布 N(a, k^2 + 1)")
# グラフのラベル
plt.title("Z の分布")
plt.xlabel("Z の値")
plt.ylabel("密度")
plt.legend()
plt.show()理論上の期待値: 1
シミュレーションによる期待値: 0.9814460670948696
理論上の標準偏差: 2.23606797749979
シミュレーションによる標準偏差: 2.2474915102454482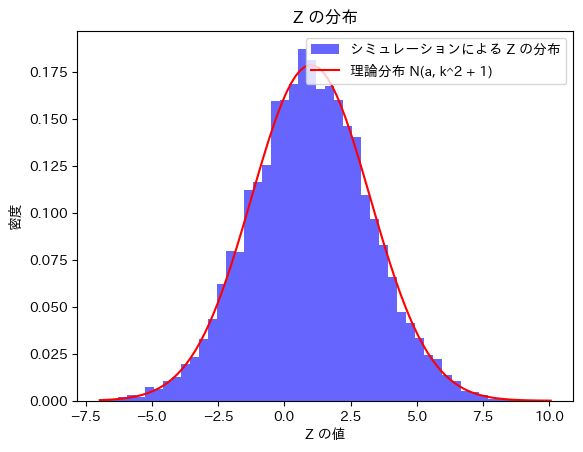
Zは![]() に従うことが確認できました。
に従うことが確認できました。
(2) 次に、XとZの相関係数をシミュレーションにより求めます。
# 2017 Q4(2) 2024.11.6
import numpy as np
import matplotlib.pyplot as plt
# 定数の設定
a = 1
k = 2
num_samples = 10000
# シミュレーション
X = np.random.normal(0, 1, num_samples)
Y = np.random.normal(0, 1, num_samples)
Z = a + k * X + Y
# 理論的な相関係数の計算
correlation_theory = k / np.sqrt(k**2 + 1)
# シミュレーションによる相関係数の計算
correlation_simulated = np.corrcoef(X, Z)[0, 1]
# 理論値とシミュレーションによる相関係数の表示
print(f"理論上の相関係数: {correlation_theory}")
print(f"シミュレーションによる相関係数: {correlation_simulated}")
# 相関係数の視覚化のための散布図のプロット
plt.figure(figsize=(8, 6))
plt.scatter(X, Z, alpha=0.5, s=10, label="X と Z の散布図")
plt.title("X と Z の相関関係")
plt.xlabel("X の値")
plt.ylabel("Z の値")
plt.legend()
plt.show()理論上の相関係数: 0.8944271909999159
シミュレーションによる相関係数: 0.8943931884333798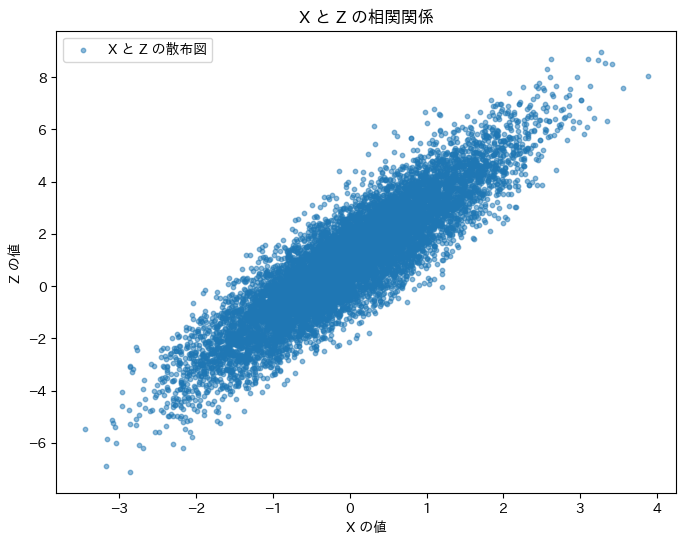
XとZの相関係数は理論値と一致しました。
(3) 次に、Z|X=xがN(a+kx,1)に従うかシミュレーションし確かめます。
# 2017 Q4(3) 2024.11.6
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 定数の設定
a = 1
k = 2
num_samples = 10000
x_fixed = 0.5 # 条件として与える X の値
# シミュレーション
Z_given_X = a + k * x_fixed + np.random.normal(0, 1, num_samples)
# 理論値の計算
mean_conditional = a + k * x_fixed
std_dev_conditional = 1 # 分散が 1 であるため
# シミュレーションによる値の計算
mean_simulation = np.mean(Z_given_X)
std_dev_simulation = np.std(Z_given_X)
# 理論値とシミュレーションによる値の表示
print(f"理論上の期待値 (Z | X = {x_fixed}): {mean_conditional}")
print(f"シミュレーションによる期待値: {mean_simulation}")
print(f"理論上の標準偏差: {std_dev_conditional}")
print(f"シミュレーションによる標準偏差: {std_dev_simulation}")
# 条件付き分布のヒストグラムのプロット
plt.hist(Z_given_X, bins=50, density=True, alpha=0.6, color='g', label=f"シミュレーションによる Z | X = {x_fixed} の分布")
# 理論分布のプロット
z_vals = np.linspace(min(Z_given_X), max(Z_given_X), 100)
plt.plot(z_vals, norm.pdf(z_vals, mean_conditional, std_dev_conditional), 'r', label="理論分布 N(a + kx, 1)")
# グラフの装飾
plt.title(f"条件付き分布 Z | X = {x_fixed}")
plt.xlabel("Z の値")
plt.ylabel("密度")
plt.legend()
plt.show()理論上の期待値 (Z | X = 0.5): 2.0
シミュレーションによる期待値: 1.978029240745398
理論上の標準偏差: 1
シミュレーションによる標準偏差: 1.0089203051741882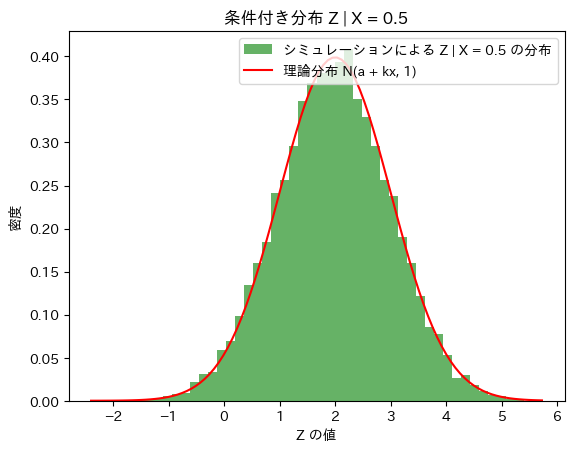
Z|X=xはN(a+kx,1)に従うことが確認できました。
2017 Q3(4)
標準化されたポアソン分布はパラメータλを∞に近づけると標準正規分布に収束することを示しました。
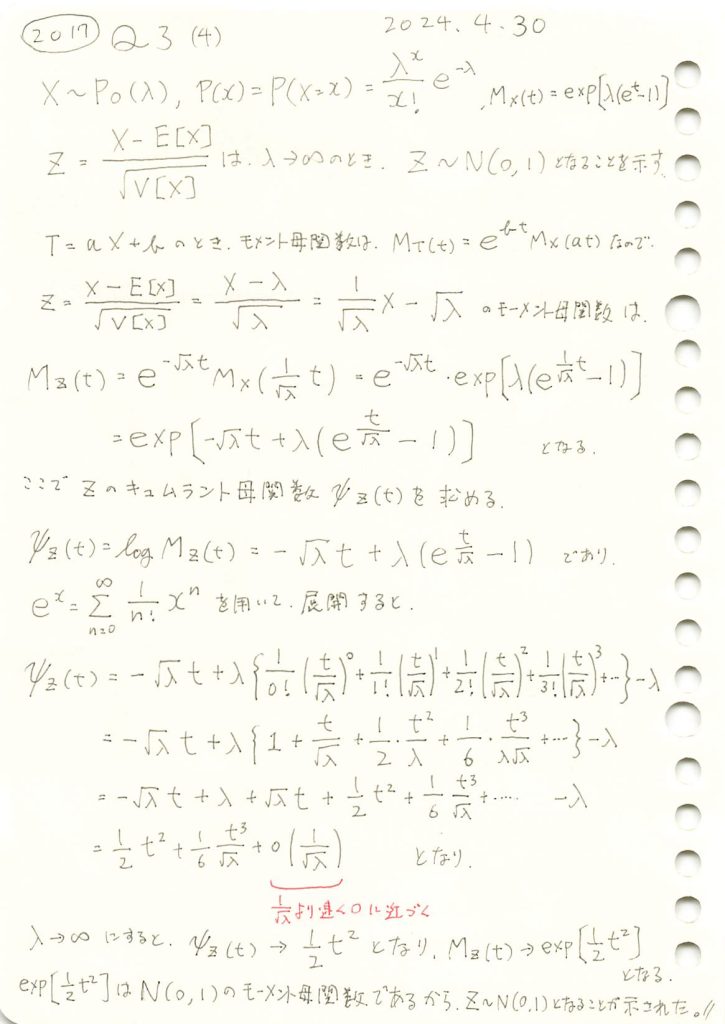
コード
λを変化させて標準化されたポアソン分布Zの分布をシミュレーションにより確認してみます。
# 2017 Q3(4) 2024.11.05
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# パラメータ設定
lambda_values = [10, 20, 50, 100]
sample_size = 10000 # サンプルサイズ
# 標準正規分布の理論値
z_values = np.linspace(-4, 4, 100)
normal_pdf = norm.pdf(z_values, 0, 1)
# 2x2 のグリッドでプロット
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
axes = axes.ravel()
# 各 λ に対してヒストグラムをプロット
for i, lambda_val in enumerate(lambda_values):
# ポアソン分布からサンプルを生成し、標準化
X_samples = np.random.poisson(lambda_val, sample_size)
Z_samples = (X_samples - lambda_val) / np.sqrt(lambda_val)
# 各 λ に対応するサブプロットでヒストグラムを描画
axes[i].hist(Z_samples, bins=100, density=True, alpha=0.5, color='orange', label=f"λ = {lambda_val}")
axes[i].plot(z_values, normal_pdf, color="red", linestyle="--", label="標準正規分布 N(0, 1)")
# グラフのカスタマイズ
axes[i].set_ylim(0, 1.8)
axes[i].set_xlabel("標準化変量 Z")
axes[i].set_ylabel("確率密度")
axes[i].set_title(f"標準化されたポアソン分布 (λ = {lambda_val})")
axes[i].legend()
axes[i].grid(True)
# レイアウト調整
plt.tight_layout()
plt.show()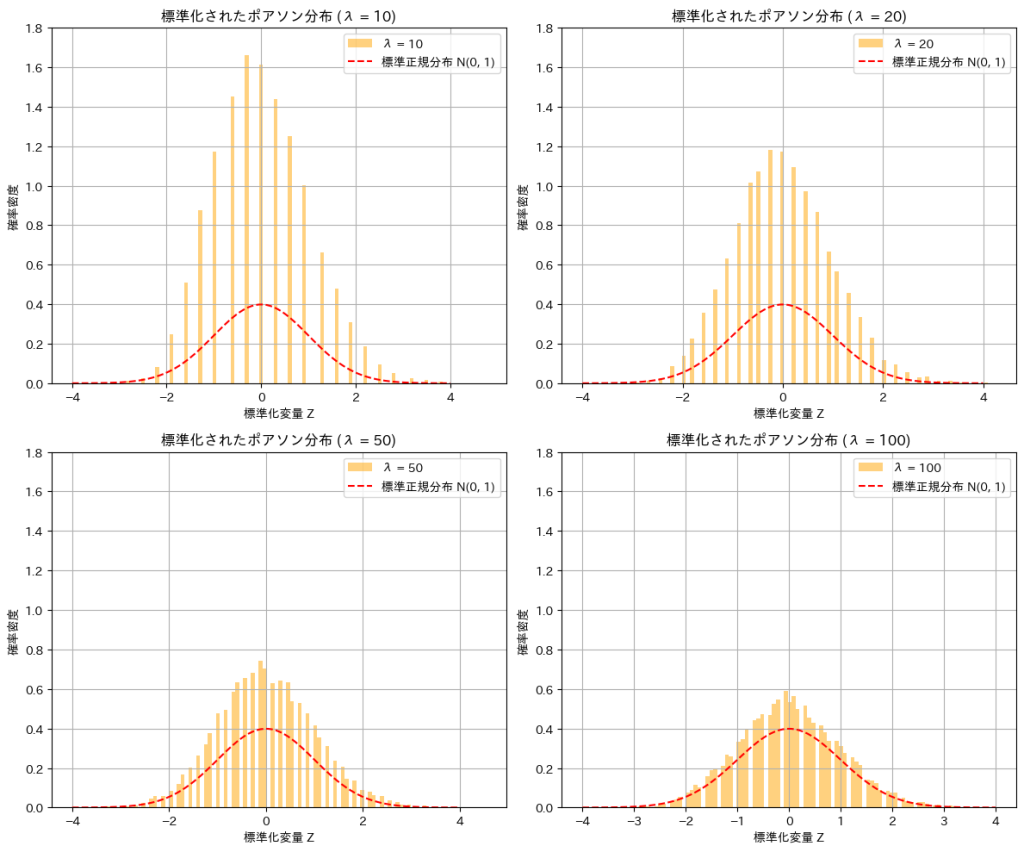
λ が増加するにつれて、標準化されたポアソン分布 Z の分布が標準正規分布に近づくことが確認できました。