2015 Q3(3)
重回帰モデルの重みの推定量の分散を求め、説明変数間の相関がそれにどのように影響するか確認しました。
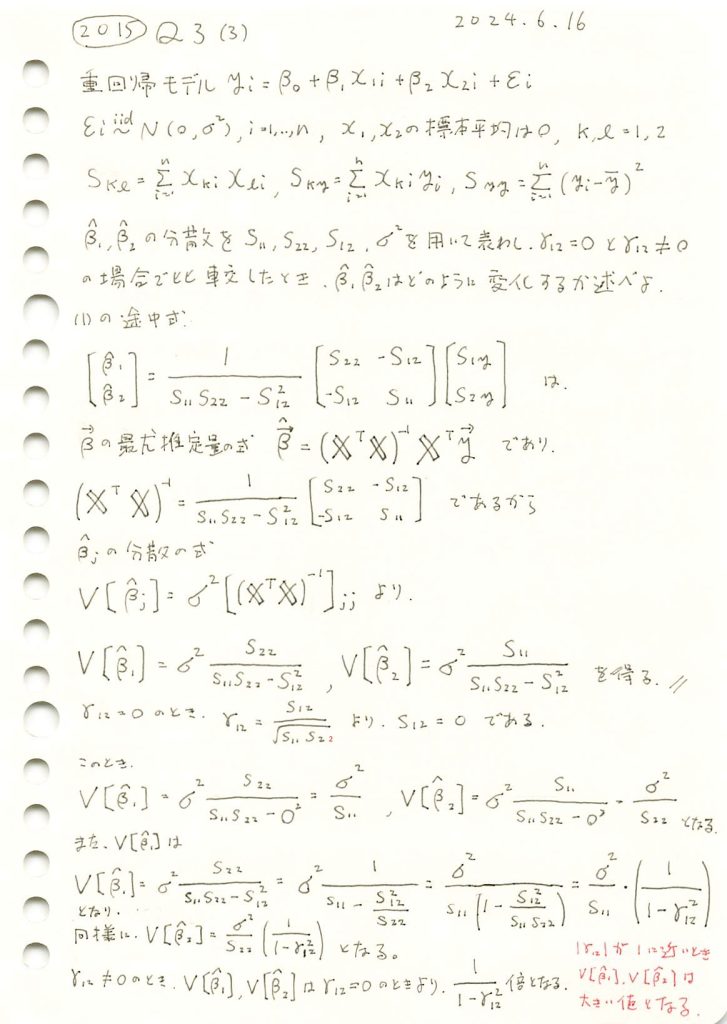
コード
![]() の変化が
の変化が![]() と
と![]() に与える影響を、グラフで描画して確認します。
に与える影響を、グラフで描画して確認します。
# 2015 Q3(3) 2024.12.14
import numpy as np
import matplotlib.pyplot as plt
# 1. パラメータ設定
r12_vals = np.linspace(-0.99, 0.99, 200) # r12の値(-0.99から0.99まで)
sigma2 = 1 # 分散 σ^2
S11 = 10 # S11の仮定値
S22 = 15 # S22の仮定値
# 2. 分散の計算
Var_beta1 = (sigma2 / S11) * (1 / (1 - r12_vals**2)) # Var(β1)
Var_beta2 = (sigma2 / S22) * (1 / (1 - r12_vals**2)) # Var(β2)
# 3. グラフのプロット
plt.figure(figsize=(10, 6))
plt.plot(r12_vals, Var_beta1, label=r'$\mathrm{Var}(\hat{\beta}_1)$', color='blue', linewidth=2)
plt.plot(r12_vals, Var_beta2, label=r'$\mathrm{Var}(\hat{\beta}_2)$', color='orange', linewidth=2)
plt.axhline(y=sigma2 / S11, color='blue', linestyle='--', label=r'$r_{12}=0$ の $\mathrm{Var}(\hat{\beta}_1)$')
plt.axhline(y=sigma2 / S22, color='orange', linestyle='--', label=r'$r_{12}=0$ の $\mathrm{Var}(\hat{\beta}_2)$')
# 軸ラベルとタイトル
plt.title(r'$\mathrm{Var}(\hat{\beta}_1)$ と $\mathrm{Var}(\hat{\beta}_2)$ の $r_{12}$ に対する変化', fontsize=14, fontweight='bold')
plt.xlabel(r'$r_{12}$($x_1$と$x_2$の相関)', fontsize=12)
plt.ylabel(r'分散', fontsize=12)
# 凡例とグリッド
plt.legend(fontsize=10, loc='upper right')
plt.grid(alpha=0.5)
# グラフ表示
plt.tight_layout()
plt.show()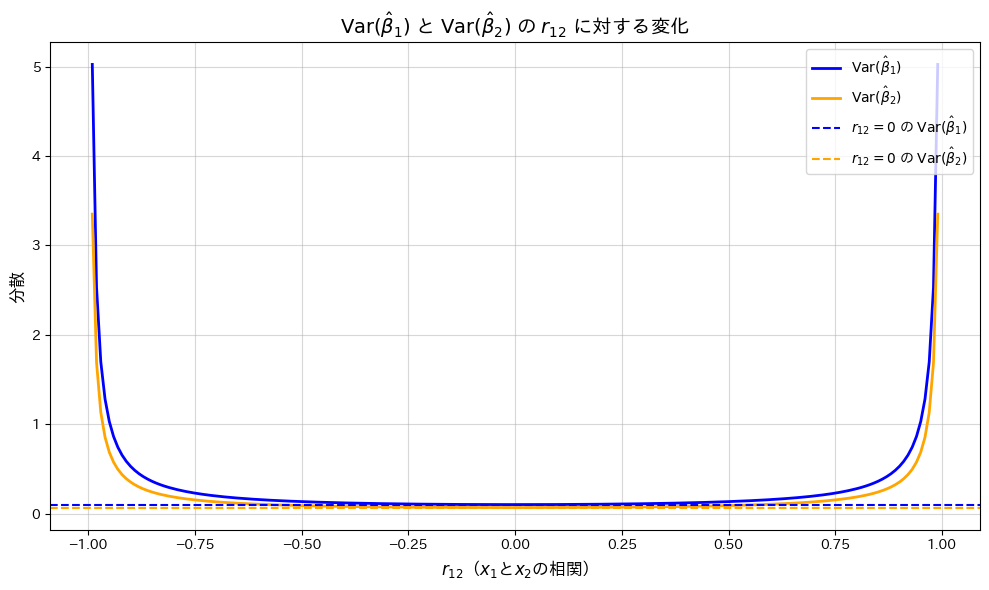
![]() が0に近いほど
が0に近いほど![]() と
と![]() は最小となり、相関が高まると分散が増加することが確認されました。
は最小となり、相関が高まると分散が増加することが確認されました。
2015 Q3(2)
重回帰モデルの重みβ1を3つの相関係数を使って表し、それが負になる必要十分条件を求めました。
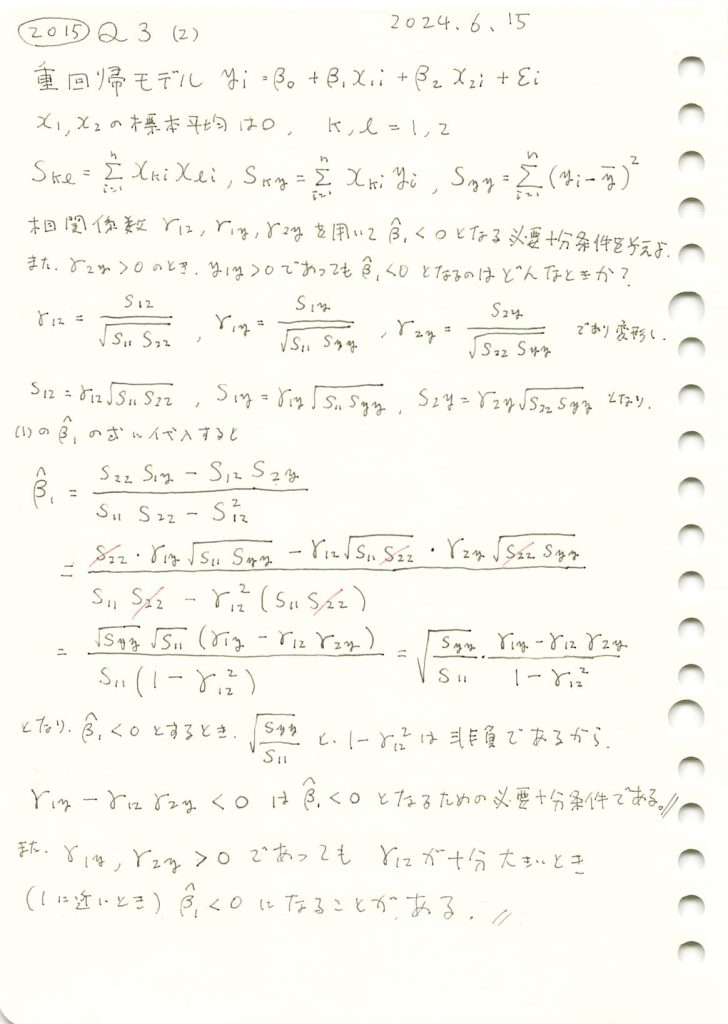
コード
![]() が大きな値をとる場合、
が大きな値をとる場合、![]() が負の値をとりやすくなることを確認するため、
が負の値をとりやすくなることを確認するため、![]() と
と![]() は、正の数に固定した上で、グラフで可視化します。
は、正の数に固定した上で、グラフで可視化します。
# 2015 Q3(2) 2024.12.13
import numpy as np
import matplotlib.pyplot as plt
# 1. パラメータの設定
n = 100 # サンプルサイズ
r12_vals = np.linspace(-0.99, 0.99, 100) # r12 を -0.99 から 0.99 まで変化させる
r1y = 0.5 # r1y を固定
r2y = 0.6 # r2y を固定
# 2. Beta1 の計算
beta1_vals = []
for r12 in r12_vals:
if abs(r12) >= 1:
beta1_vals.append(np.nan) # r12 = ±1 の場合は計算不能
continue
beta1 = (r1y - r12 * r2y) / (1 - r12**2) # 簡略化された Beta1 の符号条件
beta1_vals.append(beta1)
# 3. 結果の可視化
plt.figure(figsize=(8, 6))
plt.plot(r12_vals, beta1_vals, label=r'$\hat{\beta}_1$', color='blue')
plt.axhline(0, color='red', linestyle='--', label='ゼロライン (基準)')
plt.title(r'$\hat{\beta}_1$ と $r_{12}$ の関係', fontsize=14, fontweight='bold')
plt.xlabel(r'$r_{12}$($x_1$と$x_2$の相関)', fontsize=12)
plt.ylabel(r'$\hat{\beta}_1$', fontsize=12)
plt.legend(fontsize=10, loc='upper left')
plt.grid(alpha=0.7)
plt.tight_layout()
plt.show()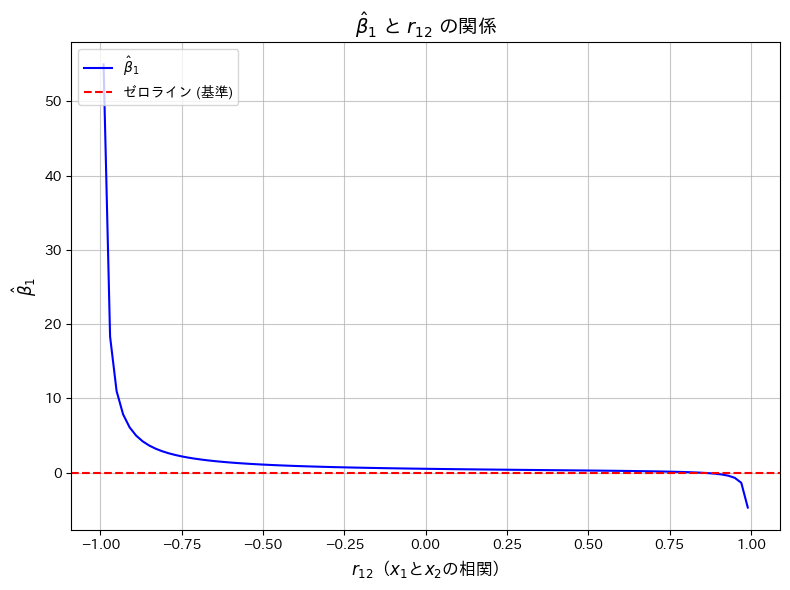
![]() が1に近い値をとると、
が1に近い値をとると、![]() が負の値をとる傾向があることが確認できました。
が負の値をとる傾向があることが確認できました。
2015 Q3(1)
重回帰モデルにおいて正規方程式を用い、各重みの最小二乗推定量を求めました。
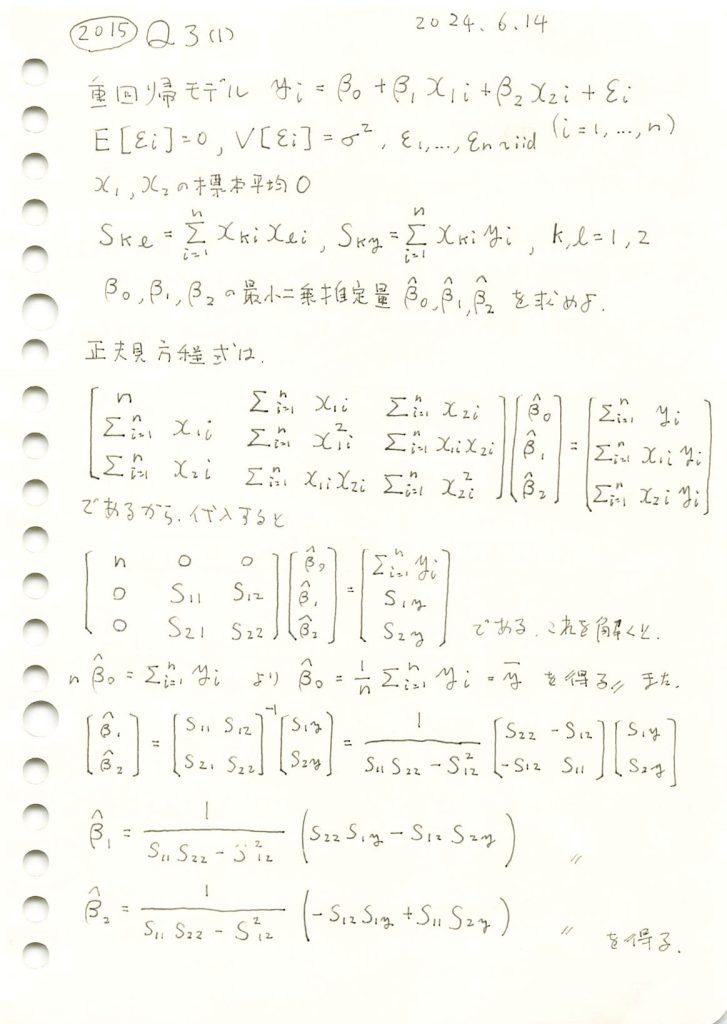
コード
重回帰モデルのシミュレーションを行い、パラメータβ0,β1,β2の推定量を計算し、真の値と比較します。
# 2015 Q3(1) 2024.12.12
import numpy as np
# 1. パラメータの設定 (再現性のため同じ設定を使用)
n = 100
beta_0, beta_1, beta_2 = 2.0, 1.0, -0.5
sigma = 1.0
# 2. 説明変数と誤差の生成
x1 = np.random.randn(n)
x2 = np.random.randn(n)
epsilon = np.random.randn(n) * sigma
# 3. 応答変数の生成
y = beta_0 + beta_1 * x1 + beta_2 * x2 + epsilon
# 4. S11, S22, S12, S1y, S2y を計算
S11 = np.sum(x1**2)
S22 = np.sum(x2**2)
S12 = np.sum(x1 * x2)
S1y = np.sum(x1 * y)
S2y = np.sum(x2 * y)
# 5. 推定値の計算 (導出した式に基づく)
denominator = S11 * S22 - S12**2
beta1_hat = (S22 * S1y - S12 * S2y) / denominator
beta2_hat = (S11 * S2y - S12 * S1y) / denominator
beta0_hat = np.mean(y) - beta1_hat * np.mean(x1) - beta2_hat * np.mean(x2)
# 推定値の表示
print(f"推定値 (導出した式):")
print(f" β0 = {beta0_hat:.3f}")
print(f" β1 = {beta1_hat:.3f}")
print(f" β2 = {beta2_hat:.3f}")
# 真の値と比較
print("\n真の値:")
print(f" β0 = {beta_0:.3f}")
print(f" β1 = {beta_1:.3f}")
print(f" β2 = {beta_2:.3f}")推定値 (導出した式):
β0 = 1.909
β1 = 0.863
β2 = -0.505
真の値:
β0 = 2.000
β1 = 1.000
β2 = -0.500シミュレーションの結果、パラメータβ0,β1,β2の推定量はわずかな誤差はあるものの、真の値に近い値を示しました。
2015 Q2(5)
前問の検定がネイマン-ピアソンの基本定理に基づき一様最強力検定であることを示しました。

コード
有意水準α=0.05のもと、検出力を理論値とシミュレーションで描画し比較します。
# 2015 Q2(5) 2024.12.11
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# シミュレーション設定
alpha = 0.05 # 有意水準
z_alpha = norm.ppf(1 - alpha) # 臨界値 z_alpha
num_simulations = 10000 # シミュレーション回数
n = 10 # 標本サイズ
mu_values = np.linspace(0, 2, 10) # 真の平均 μ の範囲
# 臨界値の計算
critical_value = z_alpha / np.sqrt(n) # 棄却域の閾値
# 検出力を計算する関数
def compute_power_for_mu(mu, n, z_alpha):
return 1 - norm.cdf(z_alpha - mu * np.sqrt(n))
# シミュレーションで検出力を計算
empirical_powers = []
for mu in mu_values:
samples = np.random.normal(mu, 1 / np.sqrt(n), num_simulations) # 標本生成
rejection_rate = np.mean(samples > critical_value) # 棄却割合
empirical_powers.append(rejection_rate)
# 理論的な検出力を計算
theoretical_powers = [compute_power_for_mu(mu, n, z_alpha) for mu in mu_values]
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(mu_values, theoretical_powers, label="理論的検出力", linestyle="--", color="blue")
plt.scatter(mu_values, empirical_powers, label="シミュレーションによる検出力", color="red", zorder=5)
plt.axhline(y=0.05, color="green", linestyle="--", label="有意水準 $\\alpha = 0.05$")
# グラフ設定
plt.xlabel("真の平均 $\\mu$", fontsize=12)
plt.ylabel("検出力 (Power)", fontsize=12)
plt.title("理論値とシミュレーションによる検出力の比較", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()
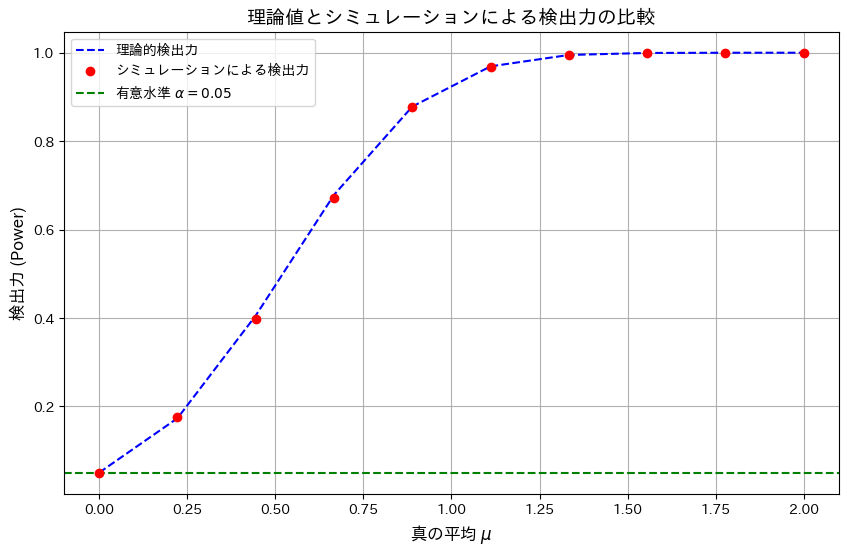
検出力は理論値とシミュレーションでよく一致し、検定が正しく機能していることを確認しました。また、真の平均μ>0に対して検出力が単調増加することが分かり、この検定が一様最強力検定の特徴を備えていることが確認できました。
2015 Q2(4)
標本平均の片側検定での検出力を特定の値以上にするために必要なサンプル数を求めました。
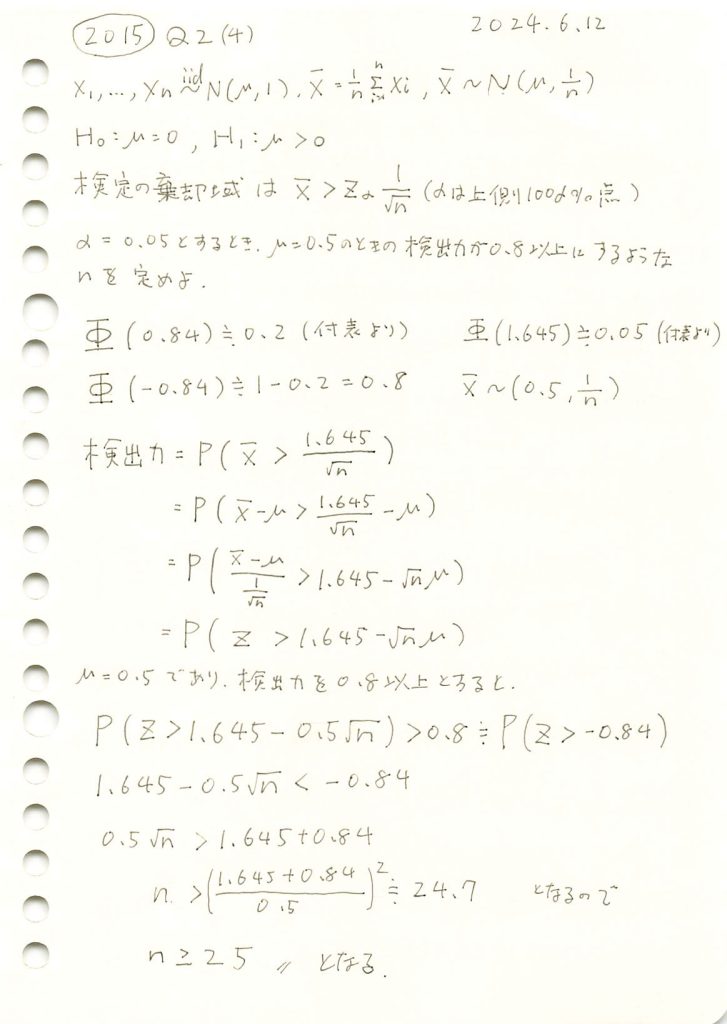
コード
有意水準α=0.05において、標本サイズnと検出力の関係を理論値とシミュレーションで比較し、目標の検出力0.8を達成するために必要な標本サイズnを調べます。
# 2015 Q2(4) 2024.12.10
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 設定
alpha = 0.05 # 有意水準
target_power = 0.8 # 目標検出力
mu = 0.5 # 真の平均
z_alpha = norm.ppf(1 - alpha) # 臨界値 z_alpha
z_power = norm.ppf(target_power) # 検出力に対応する Z 値
# 理論的な検出力の計算
n_values = np.arange(1, 51, 1) # 標本の大きさ n = 1, 2, ..., 50
powers_theoretical = [1 - norm.cdf(z_alpha - mu * np.sqrt(n)) for n in n_values]
# 実際の検出力を乱数シミュレーションで計算
num_simulations = 10000 # シミュレーション回数
n_sim_values = np.arange(5, 51, 5) # n = 5, 10, ..., 50
powers_simulated = []
for n in n_sim_values:
# 標本平均を生成
samples = np.random.normal(mu, 1 / np.sqrt(n), num_simulations)
# 標本平均が臨界値を超えた割合を計算
rejection_rate = np.mean(samples > z_alpha / np.sqrt(n))
powers_simulated.append(rejection_rate)
# グラフの描画
plt.figure(figsize=(10, 6))
# 理論的な検出力の曲線
plt.plot(n_values, powers_theoretical, label="理論的な検出力 (Power)", color="blue")
# シミュレーションによる検出力
plt.scatter(n_sim_values, powers_simulated, color="red", label="シミュレーションによる検出力", zorder=5)
# 検出力の目標ラインと必要な標本サイズライン
plt.axhline(y=target_power, color="red", linestyle="--", label=f"目標検出力 Power = {target_power}")
plt.axvline(x=25, color="green", linestyle="--", label="必要な標本数 n = 25")
# グラフの設定
plt.xlabel("標本の大きさ $n$", fontsize=12)
plt.ylabel("検出力 (Power)", fontsize=12)
plt.title("理論値とシミュレーションによる検出力の比較", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()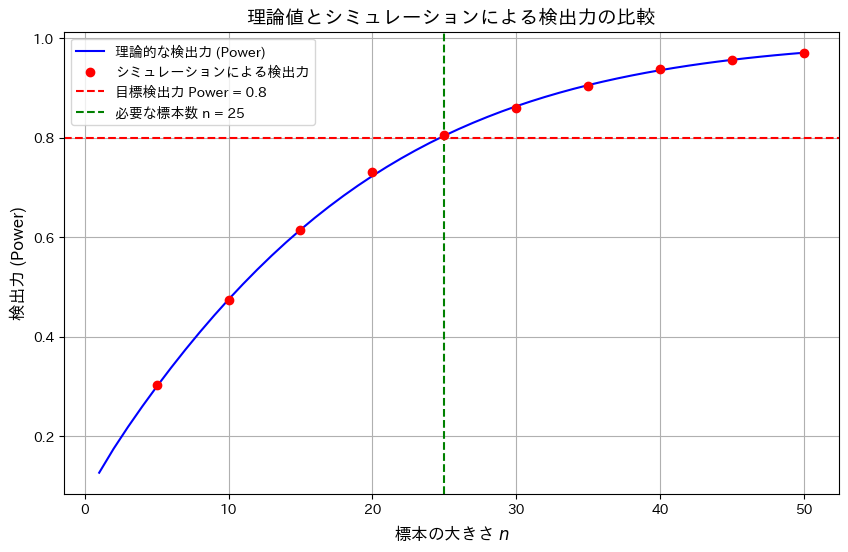
標本サイズnの増加が検出力の向上に寄与することを確認しました。また理論とシミュレーション結果が一致し、目標の検出力0.8を達成するためにはn=25が必要であることが確認できました。
2015 Q2(3)
標本平均の片側検定での検出力を求め、母平均と検出力の関係を描きました。

コード
有意水準 α=0.05、サンプルサイズ n=9およびn=16の場合における検出力を真の平均 μを変化させて視覚化します。また、μ=0.4,0.8での検出力を計算します。
# 2015 Q2(3) 2024.12.9
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 定義
alpha = 0.05 # 有意水準
z_alpha = norm.ppf(1 - alpha) # 臨界値 z_alpha
sample_sizes = [9, 16] # n = 9, 16
true_means = [0.4, 0.8] # 真の平均 μ = 0.4, 0.8
# 検出力の計算関数
def compute_power(mu, n, z_alpha):
z_value = z_alpha - mu * np.sqrt(n)
power = 1 - norm.cdf(z_value)
return power
# 検出力を計算
mu_values = np.linspace(0, 1.5, 100) # 真の平均 μ の範囲
powers_n9 = [compute_power(mu, n=9, z_alpha=z_alpha) for mu in mu_values]
powers_n16 = [compute_power(mu, n=16, z_alpha=z_alpha) for mu in mu_values]
# 指定された μ = 0.4, 0.8 の検出力を計算
specific_powers = {
(n, mu): compute_power(mu, n, z_alpha)
for n in sample_sizes
for mu in true_means
}
# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(mu_values, powers_n9, label="検出力 (n=9)", linestyle="--", color="blue")
plt.plot(mu_values, powers_n16, label="検出力 (n=16)", linestyle="-", color="green")
# μ = 0.4, 0.8 の場合の検出力をプロット
for (n, mu), power in specific_powers.items():
plt.scatter(mu, power, label=f"n={n}, μ={mu}, Power={power:.2f}", zorder=5)
# グラフの設定
plt.xlabel("真の平均 $\\mu$", fontsize=12)
plt.ylabel("検出力 (Power)", fontsize=12)
plt.title("検出力の挙動 ($n=9$ および $n=16$ の場合)", fontsize=14)
plt.axhline(y=alpha, color="red", linestyle=":", label=f"有意水準 α={alpha}")
plt.legend()
plt.grid(True)
plt.show()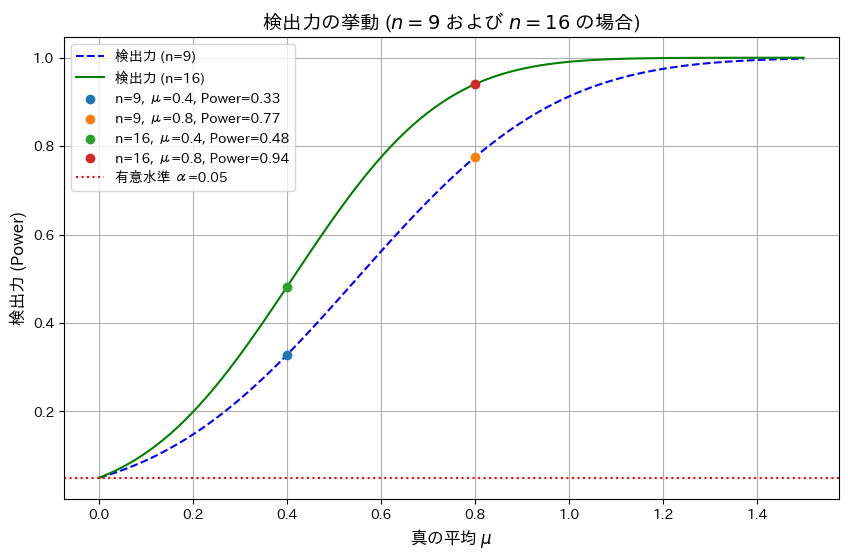
シミュレーションの結果、サンプルサイズnが増加することで検出力が向上することと、真の平均μが大きくなるほど検出力が1に近づくことが分かりました。
2015 Q2(2)
P値が有意水準より小さくなることと、観測値が棄却域より大きくなることが同等である事を示しました。

コード
標本平均![]() が棄却域に入る条件と、P値が有意水準 α以下となる条件が一致することをシミュレーションで確認します。
が棄却域に入る条件と、P値が有意水準 α以下となる条件が一致することをシミュレーションで確認します。
# 2015 Q2(2) 2024.12.8
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# シミュレーション設定
n = 10 # 標本サイズ
mu_0 = 0 # 帰無仮説の平均
sigma = 1 # 標準偏差
alpha = 0.05 # 有意水準
num_simulations = 10000 # シミュレーション回数
# z_alpha (有意水準に対応する臨界値)
z_alpha = norm.ppf(1 - alpha)
threshold = z_alpha / np.sqrt(n) # 棄却域の閾値
# シミュレーションで標本平均を生成
samples = np.random.normal(mu_0, sigma, (num_simulations, n))
x_bar = np.mean(samples, axis=1)
# 棄却域に入るかどうかを確認
in_rejection_region = x_bar > threshold
# P値の計算
p_values = 1 - norm.cdf(x_bar * np.sqrt(n) / sigma)
# P値が有意水準以下かどうかを確認
p_value_condition = p_values <= alpha
# 棄却域とP値の条件が一致する割合を計算
agreement_rate = np.mean(in_rejection_region == p_value_condition)
# 棄却域に落ちる割合とP値がα以下になる割合の比較
rejection_rate = np.mean(in_rejection_region)
p_value_rate = np.mean(p_value_condition)
# 結果の出力
print(f"シミュレーション回数: {num_simulations}")
print(f"有意水準 α: {alpha}")
print(f"棄却域条件とP値条件の一致率: {agreement_rate:.3f}")
print(f"棄却域に落ちる割合: {rejection_rate:.3f}")
print(f"P値がα以下になる割合: {p_value_rate:.3f}")
# グラフの描画
plt.figure(figsize=(12, 6))
# 標本平均 x̄ の分布
plt.hist(x_bar, bins=50, color="skyblue", alpha=0.7, edgecolor="black", label="標本平均 $\\bar{X}$ の分布")
plt.axvline(threshold, color="red", linestyle="--", label=f"棄却域の閾値 $z_{{\\alpha}}/\\sqrt{{n}} = {threshold:.3f}$")
plt.fill_betweenx([0, plt.gca().get_ylim()[1]], threshold, plt.gca().get_xlim()[1], color="red", alpha=0.2, label="棄却域")
plt.xlabel("標本平均 $\\bar{X}$", fontsize=12)
plt.ylabel("度数", fontsize=12)
plt.title("標本平均 $\\bar{X}$ の分布と棄却域", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()
# P値の分布
plt.figure(figsize=(12, 6))
plt.hist(p_values, bins=50, color="lightgreen", alpha=0.7, edgecolor="black", label="P値の分布")
plt.axvline(alpha, color="blue", linestyle="--", label=f"有意水準 $\\alpha = {alpha}$")
plt.fill_betweenx([0, plt.gca().get_ylim()[1]], 0, alpha, color="blue", alpha=0.2, label="P値が $\\leq \\alpha$ の領域")
plt.xlabel("P値", fontsize=12)
plt.ylabel("度数", fontsize=12)
plt.title("P値の分布と有意水準", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()
シミュレーション回数: 10000
有意水準 α: 0.05
棄却域条件とP値条件の一致率: 1.000
棄却域に落ちる割合: 0.052
P値がα以下になる割合: 0.052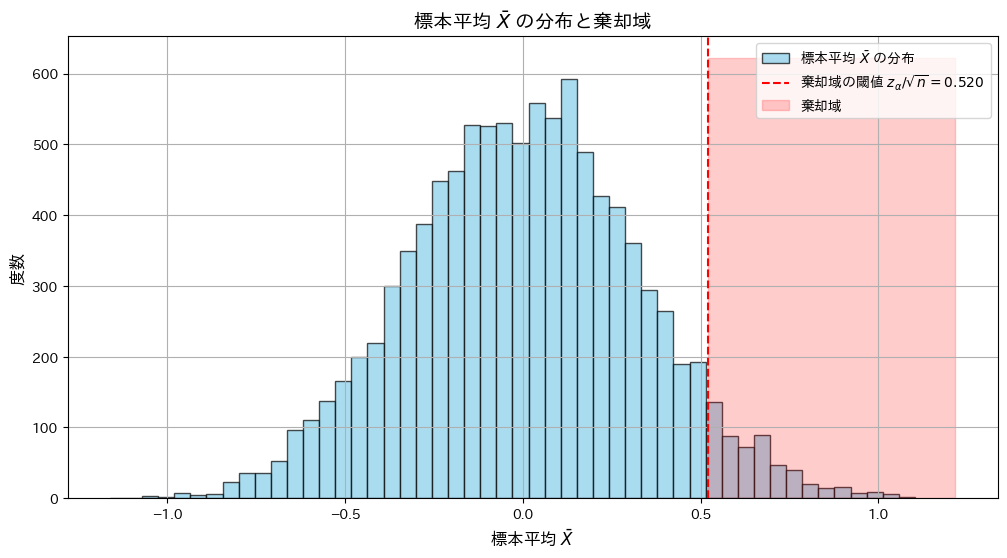
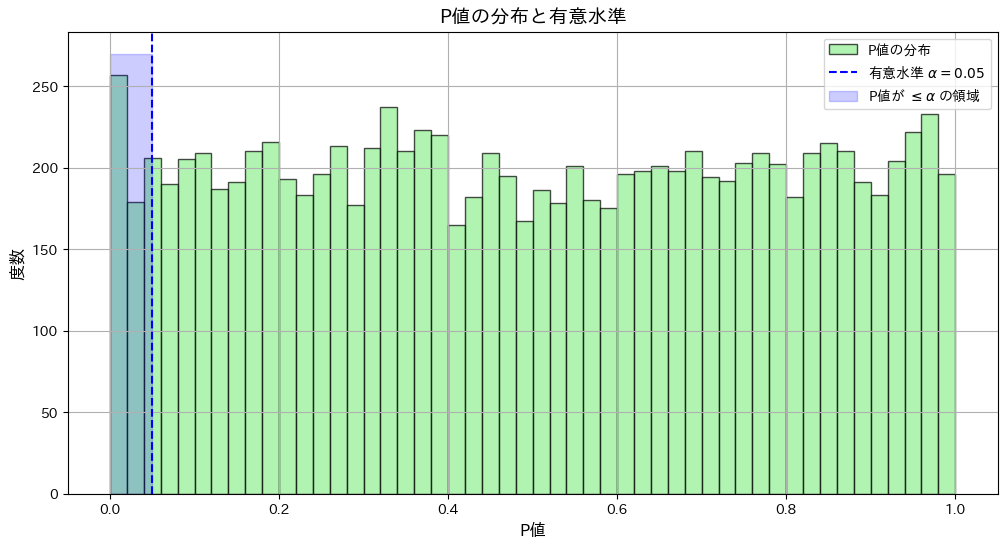
シミュレーションの結果、標本平均![]() が棄却域に入る条件と、P値が有意水準 α以下となる条件が一致しました。
が棄却域に入る条件と、P値が有意水準 α以下となる条件が一致しました。
2015 Q2(1)
標本平均とP値の関係をグラフで描きました。

コード
n=10のときの標本平均![]() とP値の関係をグラフで示します。また
とP値の関係をグラフで示します。また![]() のP値を計算します。
のP値を計算します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 問題の設定
n = 10 # サンプルサイズ
mu_0 = 0 # 帰無仮説の平均
sigma = 1 # 分散1なので標準偏差は1
alpha = 0.05 # 有意水準
critical_value = norm.ppf(1 - alpha) # 上側確率100α%点
threshold = critical_value / np.sqrt(n) # 棄却域の閾値
# 標本平均の値
x_bar_values = np.linspace(0, 1, 100) # 標本平均の範囲
p_values = 1 - norm.cdf((x_bar_values - mu_0) * np.sqrt(n)) # P値を計算
# 指定された x̄ = 0.3, 0.6 の場合の P値
x_bar_special = [0.3, 0.6]
p_values_special = 1 - norm.cdf((np.array(x_bar_special) - mu_0) * np.sqrt(n))
# 結果出力
print("指定された標本平均 x̄ に対応する P値:")
for x, p in zip(x_bar_special, p_values_special):
print(f" 標本平均 x̄ = {x:.1f} の場合の P値: {p:.3f}")
# グラフの描画
plt.figure(figsize=(8, 5))
plt.plot(x_bar_values, p_values, label="P値の挙動", color="orange")
plt.axhline(y=alpha, color="red", linestyle="--", label=f"有意水準 α={alpha}")
plt.scatter(x_bar_special, p_values_special, color="blue", label="指定点 (0.3, 0.6)")
for x, p in zip(x_bar_special, p_values_special):
plt.text(x, p, f"({x:.1f}, {p:.3f})", fontsize=10, color="blue")
plt.xlabel("標本平均 $\\bar{x}$", fontsize=12)
plt.ylabel("P値", fontsize=12)
plt.title("P値の挙動 (標本平均 $\\bar{x}$ の範囲)", fontsize=14)
plt.legend()
plt.grid(True)
plt.show()指定された標本平均 x̄ に対応する P値:
標本平均 x̄ = 0.3 の場合の P値: 0.171
標本平均 x̄ = 0.6 の場合の P値: 0.029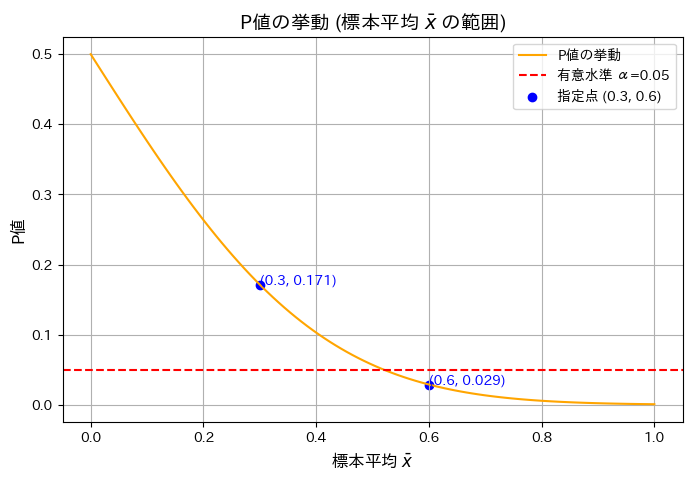
グラフの概形が描けました。標本平均![]() が大きくなるにつれてP値が減少することを確認しました。
が大きくなるにつれてP値が減少することを確認しました。
2015 Q1(5)
不偏分散の定数C倍を母分散の推定量とし平均二乗誤差を最小とするCを求めました。
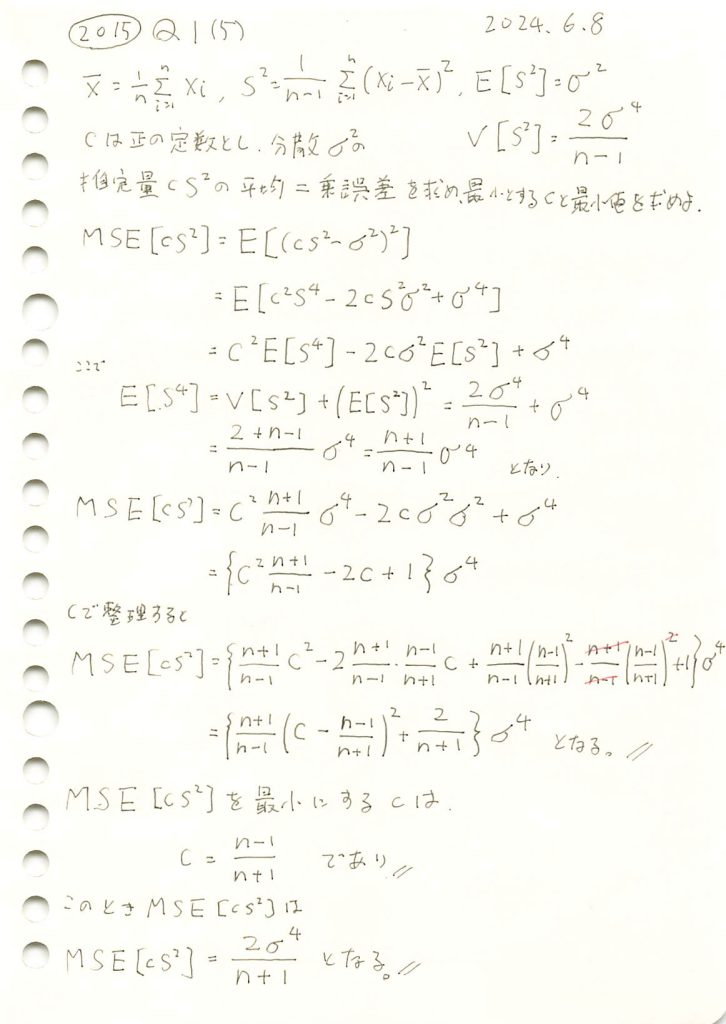
コード
![]() を最小にするcが
を最小にするcが![]() であるか確認するため、シミュレーションを行います。n=20の場合において、c≒0.9がMSEの最小になることを検証します。
であるか確認するため、シミュレーションを行います。n=20の場合において、c≒0.9がMSEの最小になることを検証します。
# 2015 Q1(5) 2024.12.6
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
sigma2 = 4 # 母分散
sigma = np.sqrt(sigma2) # 母標準偏差
n = 20 # 標本サイズ
num_simulations = 1000 # シミュレーション回数
# 理論値計算
c_theoretical = (n - 1) / (n + 1) # 理論的に最適な c
mse_theoretical_min = sigma2**2 * (2 / (n + 1)) # 最小 MSE の理論値
# シミュレーションで MSE を計算
c_values = np.linspace(0.5, 1.5, 100) # c をいろいろ変化させる
mse_simulated = []
for c in c_values:
simulated_errors = []
for _ in range(num_simulations):
sample = np.random.normal(0, sigma, n)
s2 = np.var(sample, ddof=1) # 不偏分散
error = (c * s2 - sigma2) ** 2 # 誤差の二乗
simulated_errors.append(error)
mse_simulated.append(np.mean(simulated_errors))
# グラフを描画
plt.figure(figsize=(10, 6))
plt.plot(c_values, mse_simulated, label="シミュレーションによる MSE", color='blue')
plt.axvline(c_theoretical, color='orange', linestyle='--', label=f"理論的な c={c_theoretical:.2f}")
plt.axhline(mse_theoretical_min, color='green', linestyle='--', label=f"最小理論 MSE={mse_theoretical_min:.2f}")
plt.title("MSE のシミュレーションと理論値")
plt.xlabel("c の値")
plt.ylabel("MSE")
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()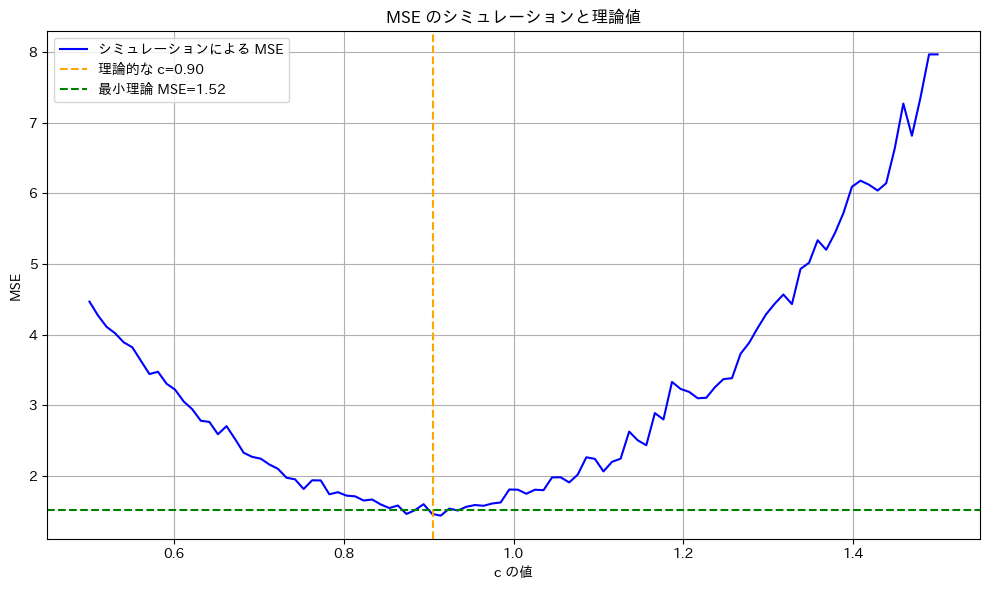
![]() は、n=20の場合において、理論通りc≒0.9のとき最小になることが確認されました。
は、n=20の場合において、理論通りc≒0.9のとき最小になることが確認されました。
2015 Q1(4)
不偏分散が母分散の一致推定量であることを確認しました。

コード
![]() が
が![]() の一致推定量であるか確認するため、
の一致推定量であるか確認するため、![]() をシミュレーションし、理論値とともにグラフで確認してみます。
をシミュレーションし、理論値とともにグラフで確認してみます。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
mu = 0 # 母平均
sigma2 = 4 # 母分散
sigma = np.sqrt(sigma2) # 母標準偏差
n_values = [10, 20, 50, 100, 200] # 標本サイズ
num_simulations = 1000 # シミュレーション回数
# 不偏分散の分散をシミュレーションで計算
simulated_variances = []
theoretical_variances = []
for n in n_values:
sample_variances = []
for _ in range(num_simulations):
sample = np.random.normal(mu, sigma, n)
unbiased_variance = np.var(sample, ddof=1) # 不偏分散
sample_variances.append(unbiased_variance)
# サンプル分散の分散を計算
var_of_sample_variance = np.var(sample_variances)
simulated_variances.append(var_of_sample_variance)
# 理論値を計算
theoretical_variance = 2 * sigma2**2 / (n - 1)
theoretical_variances.append(theoretical_variance)
# グラフの作成
plt.figure(figsize=(10, 6))
plt.plot(n_values, simulated_variances, marker='o', linestyle='-', color='blue', label="シミュレーション値")
plt.plot(n_values, theoretical_variances, marker='o', linestyle='--', color='orange', label="理論値")
# グラフの装飾
plt.title("不偏分散の分散の収束 (シミュレーション vs 理論)")
plt.xlabel("標本サイズ n")
plt.ylabel("分散 (Var[$S^2$])")
plt.grid()
plt.legend()
plt.tight_layout()
plt.show()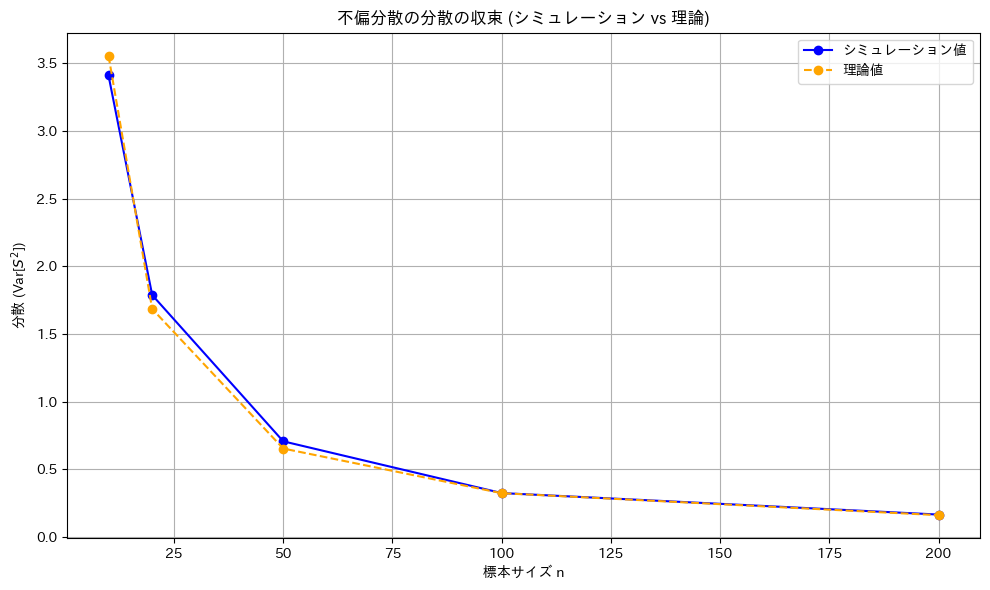
![]() のシミュレーション結果は、理論値
のシミュレーション結果は、理論値![]() とよく一致しました。また、nが増加すると分散が0に近づき、
とよく一致しました。また、nが増加すると分散が0に近づき、![]() が
が![]() の一致推定量であることが確認できました。
の一致推定量であることが確認できました。