2015 Q5(3)
2つに分けられた組標本のそれぞれ平均と不偏分散の具体的な値から、全体の平均と不偏分散および相関係数を計算しました。
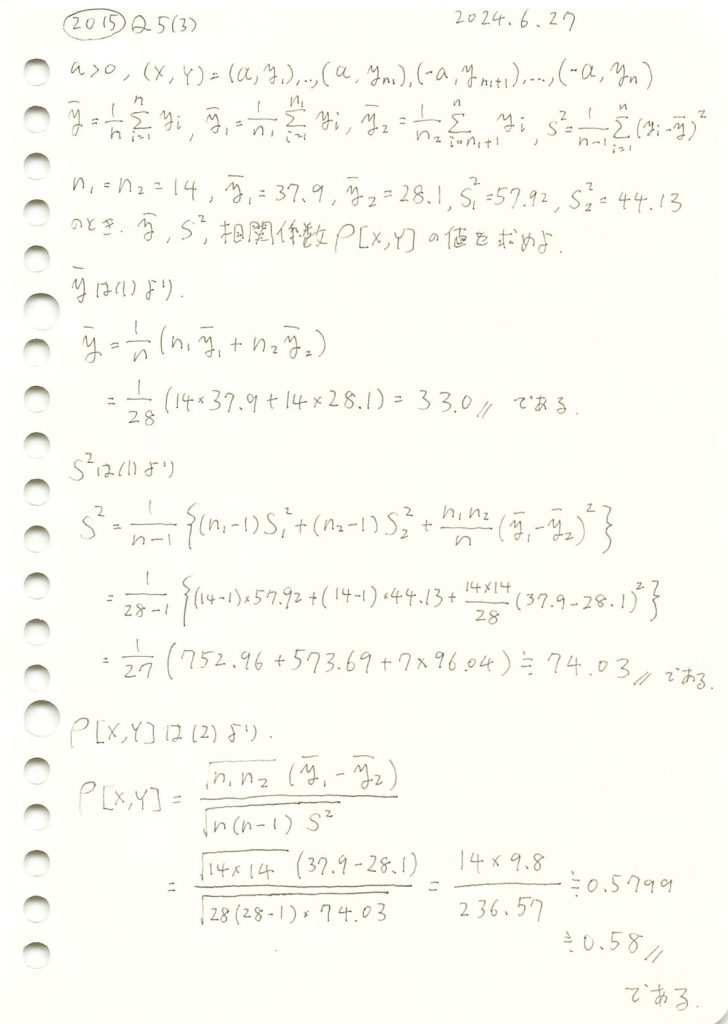
コード
与えられたデータを基に、全体の平均と分散を計算し、相関係数を求めます。
# 2015 Q5(3) 2024.12.24
# 与えられたデータ
n1 = n2 = 14
n = n1 + n2
y1_bar = 37.9
y2_bar = 28.1
s1_sq = 57.92
s2_sq = 44.13
# 全体の平均
y_bar = (n1 * y1_bar + n2 * y2_bar) / n
# 全体の分散
s_sq = (
((n1 - 1) * s1_sq + (n2 - 1) * s2_sq) / (n - 1)
+ (n1 * n2 / n) * ((y1_bar - y2_bar) ** 2) / (n - 1)
)
# 相関係数
numerator = (n1 * n2) ** 0.5 * (y1_bar - y2_bar)
denominator = (n * (n - 1) * s_sq) ** 0.5
r = numerator / denominator
# 結果出力
print("全体の平均 (y_bar):", y_bar)
print("全体の分散 (s^2):", s_sq)
print("相関係数 (r):", r)全体の平均 (y_bar): 33.0
全体の分散 (s^2): 74.03444444444443
相関係数 (r): 0.5799309710329085与えられたデータを基に、全体の平均と分散を計算し、相関係数を求め、解答と一致することを確認しました。
2015 Q5(2)
組標本の相関係数を、2つに分けられた組標本のそれぞれ平均と全体の不偏分散で表現しました。

コード
与えられた式を用いて計算した相関系数と、通常の定義式を用いて計算した相関係数が一致するかシミュレーションで確認をします。
# 2015 Q5(2) 2024.12.23
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータ
n1 = 30 # グループ1のサンプル数
n2 = 20 # グループ2のサンプル数
n = n1 + n2 # 全体のサンプル数
simulations = 1000 # シミュレーションの回数
# 結果を格納するリスト
custom_r_values = [] # 式で計算した相関係数
standard_r_values = [] # 通常の相関係数
for _ in range(simulations):
# y の生成 (正規分布)
y1 = np.random.normal(0, 1, n1)
y2 = np.random.normal(0, 1, n2)
y = np.concatenate([y1, y2])
# a の生成
a_values = np.concatenate([np.full(n1, 1), np.full(n2, -1)])
# 平均と分散
y_bar = np.mean(y)
s_sq_y = np.var(y, ddof=1)
# 共分散
covariance_manual = np.mean((y - y_bar) * (a_values - np.mean(a_values)))
# 通常の相関係数
standard_r = covariance_manual / np.sqrt(s_sq_y * np.var(a_values, ddof=1))
standard_r_values.append(standard_r)
# 式での相関係数
y1_bar = np.mean(y1)
y2_bar = np.mean(y2)
numerator_custom = np.sqrt(n1 * n2) * (y1_bar - y2_bar)
denominator_custom = np.sqrt(n * (n - 1) * s_sq_y)
custom_r = numerator_custom / denominator_custom
custom_r_values.append(custom_r)
# グラフの描画
plt.figure(figsize=(8, 8))
plt.scatter(custom_r_values, standard_r_values, alpha=0.5, color='blue', label=r"$r = \frac{\sqrt{n_1 n_2} (\bar{y}_1 - \bar{y}_2)}{\sqrt{n(n-1)s^2}}$")
plt.plot([min(custom_r_values), max(custom_r_values)], [min(custom_r_values), max(custom_r_values)], color='red', linestyle='--', label=r"$r = \frac{\mathrm{Cov}(X, Y)}{\sqrt{\mathrm{Var}(X)\mathrm{Var}(Y)}}$")
plt.title("相関係数の比較", fontsize=14)
plt.xlabel("式による相関係数", fontsize=12)
plt.ylabel("通常の相関係数", fontsize=12)
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()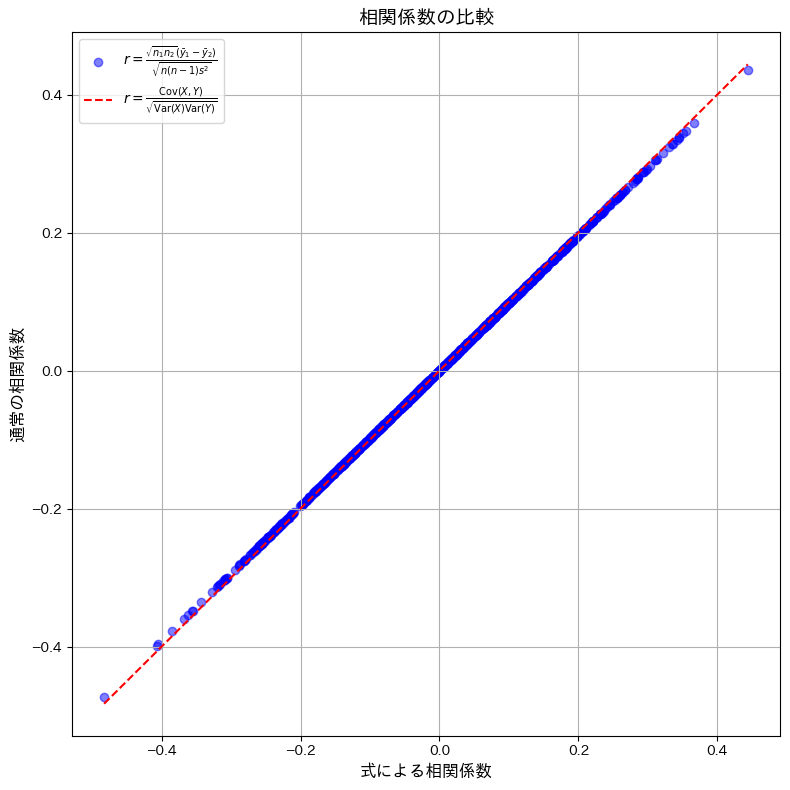
与えられた式を用いて計算した相関系数と、通常の定義式を用いて計算した相関係数が一致しました。わずかに観測された誤差は、浮動小数点演算による丸め誤差であると考えられます。
2015 Q5(1)
2つに分けられた標本それぞれの平均と不偏分散を用い、元の平均と不偏分散を式で表しました。

コード
直接アプローチと間接アプローチで求めた![]() と
と![]() が一致するか確認をします。
が一致するか確認をします。
# 2015 Q5(1) 2024.12.22
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータ
n1 = 30 # グループ1のサンプル数
n2 = 20 # グループ2のサンプル数
n = n1 + n2 # 全体のサンプル数
simulations = 10000 # シミュレーションの回数
# 結果を格納するリスト
y_split = [] # 分割アプローチで計算した平均
y_direct = [] # 直接アプローチで計算した平均
s2_split = [] # 分割アプローチで計算した分散
s2_direct = [] # 直接アプローチで計算した分散
for _ in range(simulations):
# ランダムサンプル生成 (正規分布 N(0, 1) を仮定)
group1 = np.random.normal(0, 1, n1)
group2 = np.random.normal(0, 1, n2)
# グループごとの平均と分散
y1_bar = np.mean(group1)
y2_bar = np.mean(group2)
s1_sq = np.var(group1, ddof=1) # 分散 (不偏推定)
s2_sq = np.var(group2, ddof=1)
# 分割アプローチの平均と分散
y_bar_split = (n1 * y1_bar + n2 * y2_bar) / n
s_sq_split = (
((n1 - 1) * s1_sq + (n2 - 1) * s2_sq) / (n - 1)
+ (n1 * n2 / n) * (y1_bar - y2_bar) ** 2 / (n - 1)
)
# 直接アプローチの平均と分散
all_data = np.concatenate([group1, group2])
y_bar_direct = np.mean(all_data)
s_sq_direct = np.var(all_data, ddof=1)
# データを格納
y_split.append(y_bar_split)
y_direct.append(y_bar_direct)
s2_split.append(s_sq_split)
s2_direct.append(s_sq_direct)
# グラフの描画
fig, axes = plt.subplots(1, 2, figsize=(16, 8))
# 平均の比較
axes[0].scatter(y_split, y_direct, alpha=0.5, color='blue', label=r"分割アプローチ: $\bar{y} = \frac{1}{n}(n_1\bar{y}_1 + n_2\bar{y}_2)$")
axes[0].plot([min(y_split), max(y_split)], [min(y_split), max(y_split)], color='red', linestyle='--', label=r"直接アプローチ: $\bar{y} = \frac{1}{n} \sum_{i=1}^n y_i$")
axes[0].set_xlabel('分割アプローチ (平均)', fontsize=12)
axes[0].set_ylabel('直接アプローチ (平均)', fontsize=12)
axes[0].set_title('平均の比較: 分割 vs 直接', fontsize=14)
axes[0].legend()
axes[0].grid(True)
# 分散の比較
axes[1].scatter(s2_split, s2_direct, alpha=0.5, color='green', label=r"分割アプローチ: $s^2 = \frac{1}{n-1} \left\{(n_1-1)s_1^2 + (n_2-1)s_2^2 + \frac{n_1n_2}{n}(\bar{y}_1 - \bar{y}_2)^2 \right\}$")
axes[1].plot([min(s2_split), max(s2_split)], [min(s2_split), max(s2_split)], color='red', linestyle='--', label=r"直接アプローチ: $s^2 = \frac{1}{n-1}\sum_{i=1}^n (y_i - \bar{y})^2$")
axes[1].set_xlabel('分割アプローチ (分散)', fontsize=12)
axes[1].set_ylabel('直接アプローチ (分散)', fontsize=12)
axes[1].set_title('分散の比較: 分割 vs 直接', fontsize=14)
axes[1].legend()
axes[1].grid(True)
# グラフの表示
plt.tight_layout()
plt.show()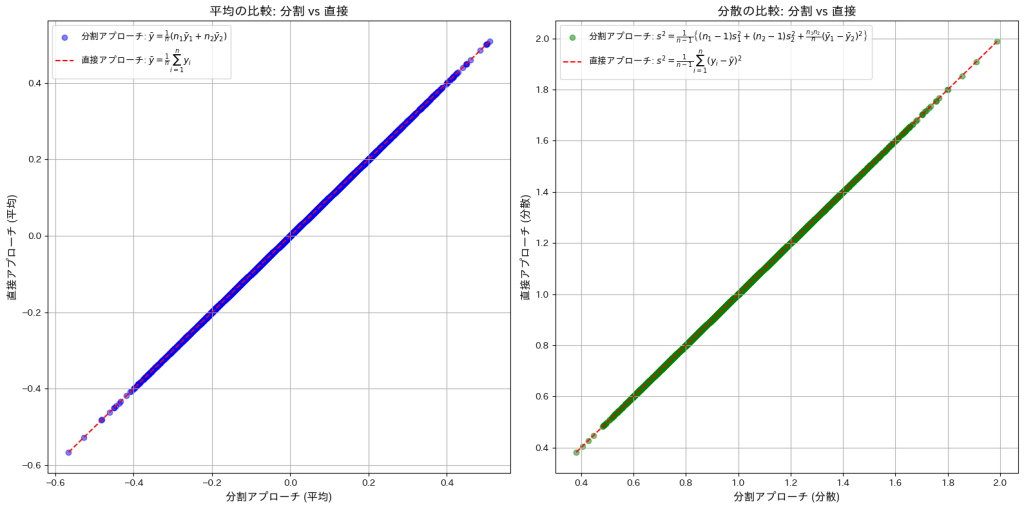
直接アプローチと間接アプローチで求めた![]() と
と![]() が一致しました。
が一致しました。
2015 Q4(5)
確率行列が対称行列であるとき、ある新しいパラメータ行列も対称であるか示し、更にその逆が成り立つかも調べました。

コード
セル確率![]() の対称性が成り立つ場合にパラメータ
の対称性が成り立つ場合にパラメータ![]() が対称性
が対称性![]() を持つことを確認します。
を持つことを確認します。
# 2015 Q4(5) 2024.12.21
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# 1. データ生成
np.random.seed(42) # 再現性のためのシード値
I = 4 # 行列のサイズ
p_matrix_sym = np.random.rand(I, I) # 対称性を持たないランダムな確率行列
p_matrix_sym = (p_matrix_sym + p_matrix_sym.T) / 2 # 対称性を強制
# 対称性が成り立たない確率行列
p_matrix_asym = np.random.rand(I, I)
p_matrix_asym = p_matrix_asym / np.sum(p_matrix_asym) # 正規化
# 正規化して確率にする
p_matrix_sym = p_matrix_sym / np.sum(p_matrix_sym)
# 2. λ_ij の計算関数
def calculate_lambda(p_matrix):
I = p_matrix.shape[0]
lambdas = np.zeros((I, I))
for i in range(1, I):
for j in range(1, I):
lambdas[i, j] = np.log(p_matrix[i, j] * p_matrix[0, 0] / (p_matrix[i, 0] * p_matrix[0, j]))
return lambdas
# 対称性の仮説が成り立つ場合の λ_ij
lambda_sym = calculate_lambda(p_matrix_sym)
# 対称性の仮説が成り立たない場合の λ_ij
lambda_asym = calculate_lambda(p_matrix_asym)
# 3. 可視化: ヒートマップをプロット
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
# 対称性が成り立つ確率行列
sns.heatmap(p_matrix_sym, annot=True, fmt=".3f", cmap="Blues", ax=axes[0, 0])
axes[0, 0].set_title("対称性が成り立つ確率行列 $p_{ij}$")
# 対称性が成り立つ λ_ij 行列
sns.heatmap(lambda_sym, annot=True, fmt=".3f", cmap="Greens", ax=axes[0, 1])
axes[0, 1].set_title("対称性が成り立つ場合の $\lambda_{ij}$")
# 対称性が成り立たない確率行列
sns.heatmap(p_matrix_asym, annot=True, fmt=".3f", cmap="Reds", ax=axes[1, 0])
axes[1, 0].set_title("対称性が成り立たない確率行列 $p_{ij}$")
# 対称性が成り立たない λ_ij 行列
sns.heatmap(lambda_asym, annot=True, fmt=".3f", cmap="Purples", ax=axes[1, 1])
axes[1, 1].set_title("対称性が成り立たない場合の $\lambda_{ij}$")
plt.tight_layout()
plt.show()
# 4. λ_ij = λ_ji の確認
print("対称性が成り立つ場合:")
print("λ_ij == λ_ji:", np.allclose(lambda_sym, lambda_sym.T))
print("\n対称性が成り立たない場合:")
print("λ_ij == λ_ji:", np.allclose(lambda_asym, lambda_asym.T))
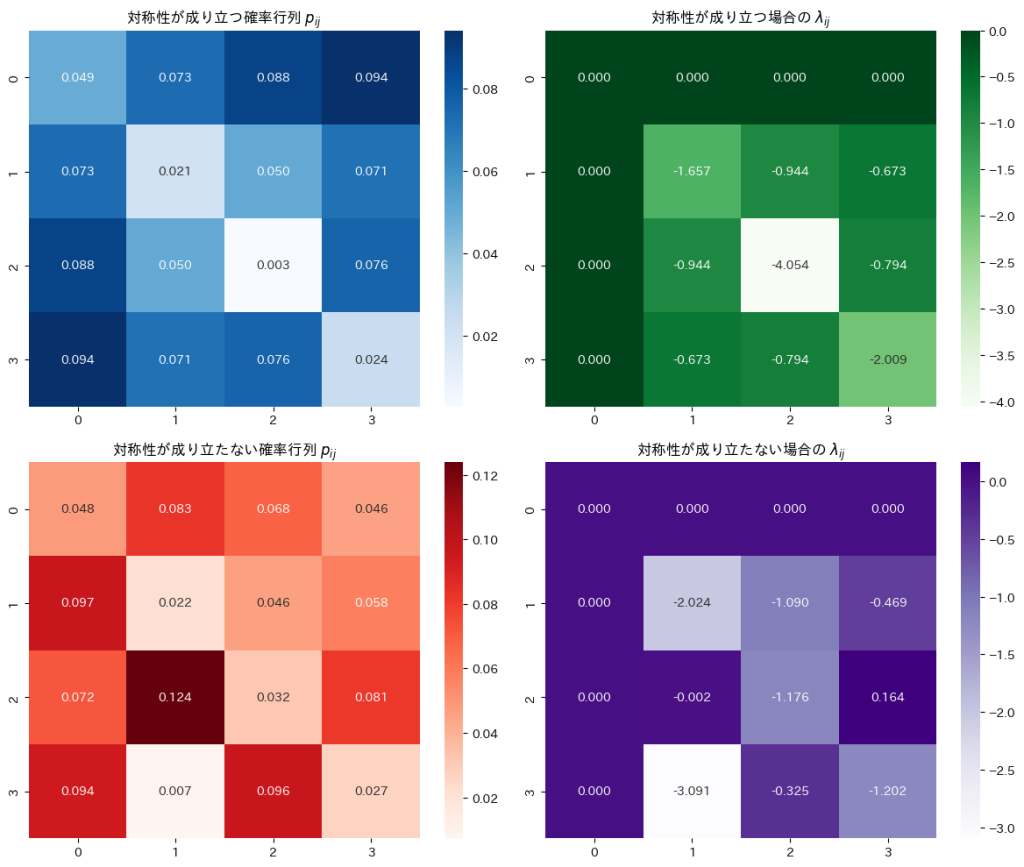
セル確率![]() の対称性が成り立つ場合に、パラメータ
の対称性が成り立つ場合に、パラメータ![]() が対称性
が対称性![]() を持つことを確認しました。
を持つことを確認しました。
2015 Q4(4)
確率の正方行列と新しいパラメータが相互に変換可で一対一であることを確認しました。

コード
セル確率![]() を新しいパラメータ
を新しいパラメータ![]() に変換し、その逆変換を用いて元の
に変換し、その逆変換を用いて元の![]() を再構成することで、変換が一対一であることを確認します。
を再構成することで、変換が一対一であることを確認します。
import numpy as np
# セル確率 p_ij を与える (例として 3x3 の行列を使用)
p_ij = np.array([[0.2, 0.1, 0.05],
[0.15, 0.25, 0.05],
[0.05, 0.05, 0.1]])
I = p_ij.shape[0]
# 1. 与えられた p_ij から θ_i, φ_j, λ_ij を計算
p_11 = p_ij[0, 0] # p_11 はセル (1, 1) の確率
theta_i = np.log(p_ij[1:, 0] / p_11) # θ_i = log(p_i1 / p_11), i = 2, ..., I
phi_j = np.log(p_ij[0, 1:] / p_11) # φ_j = log(p_1j / p_11), j = 2, ..., I
lambda_ij = np.zeros((I - 1, I - 1)) # λ_ij を初期化
for i in range(1, I):
for j in range(1, I):
lambda_ij[i - 1, j - 1] = np.log(p_ij[i, j] * p_11 / (p_ij[i, 0] * p_ij[0, j]))
# 2. θ_i, φ_j, λ_ij から p_ij を再構成
p_ij_reconstructed = np.zeros_like(p_ij)
p_ij_reconstructed[0, 0] = 1 / (
1 +
np.sum(np.exp(theta_i)) +
np.sum(np.exp(phi_j)) +
np.sum(np.exp(theta_i[:, None] + phi_j[None, :] + lambda_ij))
)
# 再構成した確率の計算
for i in range(I):
for j in range(I):
if i == 0 and j > 0: # p_1j
p_ij_reconstructed[i, j] = p_ij_reconstructed[0, 0] * np.exp(phi_j[j - 1])
elif j == 0 and i > 0: # p_i1
p_ij_reconstructed[i, j] = p_ij_reconstructed[0, 0] * np.exp(theta_i[i - 1])
elif i > 0 and j > 0: # p_ij
p_ij_reconstructed[i, j] = p_ij_reconstructed[0, 0] * np.exp(
theta_i[i - 1] + phi_j[j - 1] + lambda_ij[i - 1, j - 1]
)
# 3. 結果を確認
print("元の p_ij:")
print(p_ij)
print("\n再構成した p_ij:")
print(p_ij_reconstructed)
# 一致を確認
if np.allclose(p_ij, p_ij_reconstructed, atol=1e-10):
print("\n与えられた p_ij と再構成した p_ij は一致しました!変換は一対一です。")
else:
print("\n再構成した p_ij が元の p_ij と一致しません。")元の p_ij:
[[0.2 0.1 0.05]
[0.15 0.25 0.05]
[0.05 0.05 0.1 ]]
再構成した p_ij:
[[0.2 0.1 0.05]
[0.15 0.25 0.05]
[0.05 0.05 0.1 ]]
与えられた p_ij と再構成した p_ij は一致しました!変換は一対一です。与えられたセル確率![]() と、再構成したセル確率
と、再構成したセル確率![]() は一致しました。このことから、変換が一対一であることが確認されました。
は一致しました。このことから、変換が一対一であることが確認されました。
2015 Q4(3)
確率の分割表に対称性があるという仮説の下での尤度比検定を行いp値が0.01より小さいか判定しました。

コード
![]() が成り立つかを確認するために、尤度比検定量
が成り立つかを確認するために、尤度比検定量![]() を求め、尤度比検定を行います。
を求め、尤度比検定を行います。
# 2015 Q4(3) 2024.12.19
import numpy as np
from scipy.stats import chi2
# 観測度数表
observed_counts = np.array([[1520, 266, 124, 66],
[234, 1512, 432, 78],
[117, 362, 1772, 205],
[36, 82, 179, 492]])
I = observed_counts.shape[0] # 行・列のサイズ
# 尤度比統計量 G^2 の計算 (対角要素を除外)
G2 = 2 * sum(
observed_counts[i, j] * np.log(2 * observed_counts[i, j] / (observed_counts[i, j] + observed_counts[j, i]))
for i in range(I) for j in range(I) if i != j
)
# 自由度の計算 (非対角要素の数: I(I-1)/2)
df = (I * (I - 1)) // 2
# P値の計算
p_value = 1 - chi2.cdf(G2, df)
# 結果の表示
print(f"尤度比統計量 G^2: {G2:.4f}")
print(f"自由度: {df}")
print(f"P値: {p_value:.10f}")
# 帰無仮説の判定
if p_value < 0.01:
print("P値は0.01より小さいため、帰無仮説 H_0 は棄却されます。")
else:
print("P値は0.01以上のため、帰無仮説 H_0 は棄却されません。")
尤度比統計量 G^2: 19.2492
自由度: 6
P値: 0.0037628518
P値は0.01より小さいため、帰無仮説 H_0 は棄却されます。P値は0.01より小さいため、帰無仮説 ![]() は棄却されました。
は棄却されました。
2015 Q4(2)
確率の分割表に対称性があるという仮説の下での期待度数の最尤推定を行いました。
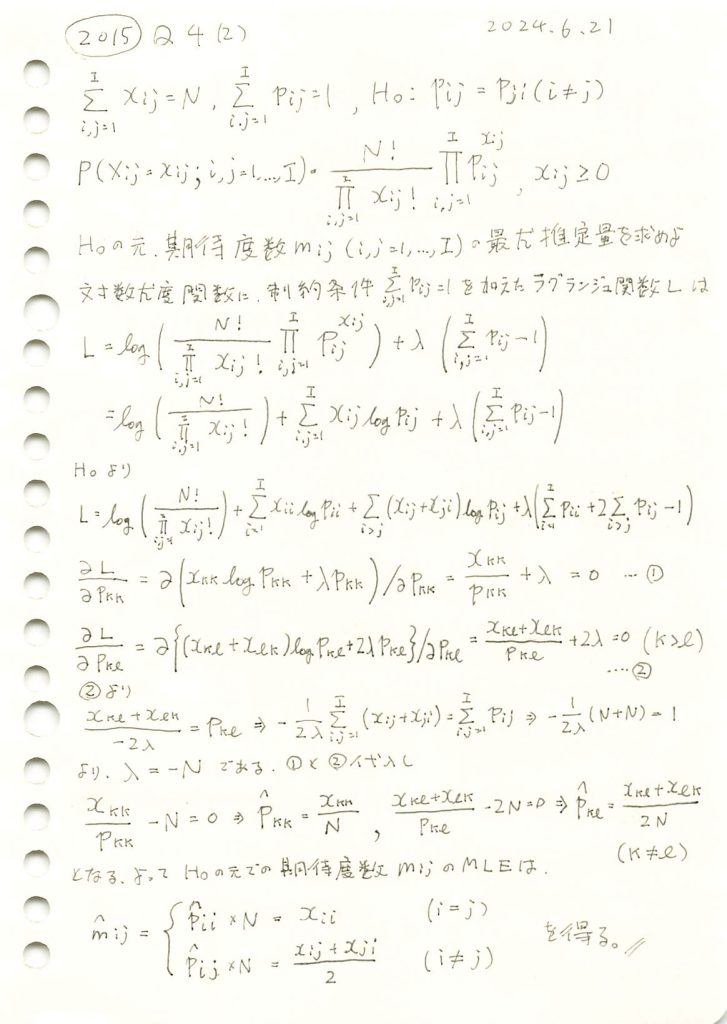
与えられた観測度数表から![]() に基づき期待度数を求めます。
に基づき期待度数を求めます。
# 2015 Q4(2) 2024.12.18
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 1. 観測度数表
observed_counts = np.array([[1520, 266, 124, 66],
[234, 1512, 432, 78],
[117, 362, 1772, 205],
[36, 82, 179, 492]])
# 2. 総サンプルサイズ N
N = observed_counts.sum()
# 3. 期待度数 m_ij の計算 (対称性の仮説)
m_ij = np.zeros_like(observed_counts, dtype=float)
I = observed_counts.shape[0]
for i in range(I):
for j in range(I):
if i == j: # 対角要素
m_ij[i, j] = observed_counts[i, j]
else: # 非対角要素
m_ij[i, j] = (observed_counts[i, j] + observed_counts[j, i]) / 2
# 4. 観測度数と期待度数をDataFrameにまとめる
row_labels = col_labels = ["Highest", "Second", "Third", "Lowest"]
df_observed = pd.DataFrame(observed_counts, index=row_labels, columns=col_labels)
df_expected = pd.DataFrame(np.round(m_ij, 2), index=row_labels, columns=col_labels)
# 5. 観測度数と期待度数のヒートマップを作成
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
# 観測度数のヒートマップ
sns.heatmap(df_observed, annot=True, fmt=".0f", cmap="Blues", ax=axes[0])
axes[0].set_title("観測度数表 $x_{ij}$")
# 期待度数のヒートマップ
sns.heatmap(df_expected, annot=True, fmt=".2f", cmap="Greens", ax=axes[1])
axes[1].set_title("期待度数表 $\hat{m}_{ij}$ (対称性の仮説)")
plt.tight_layout()
plt.show()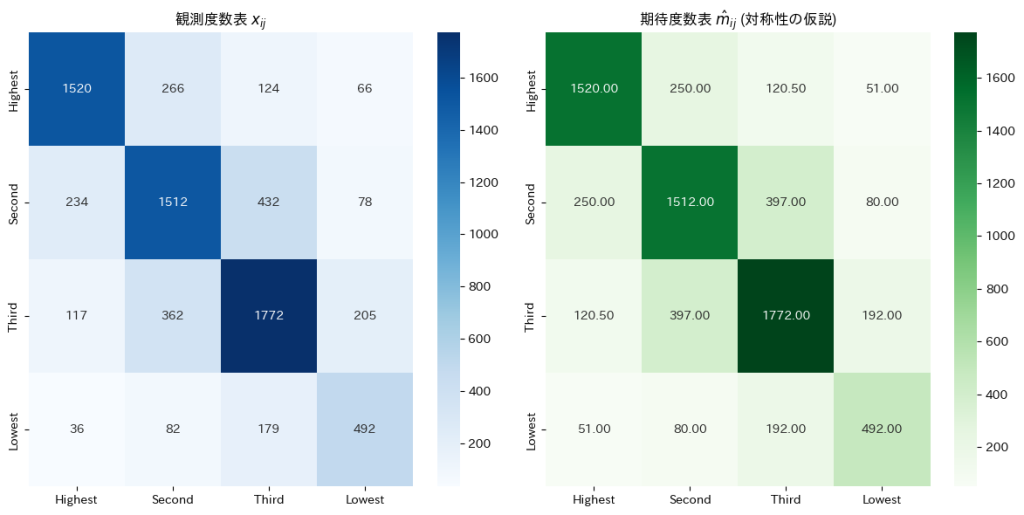
与えられた観測度数表から![]() に基づいて期待度数を求めると、非対角要素は対応する2つの観測度数の平均として表され、対角要素は観測度数そのものが期待度数となりました。
に基づいて期待度数を求めると、非対角要素は対応する2つの観測度数の平均として表され、対角要素は観測度数そのものが期待度数となりました。
2015 Q4(1)
観測度数と確率の分割表から、そうなり得る確率を求めました。

コード
与えられた観測度数表から仮にセル確率を計算し、その観測度数が多項分布に基づいて得られる確率を計算をします。
# 2015 Q4(1) 2024.12.17
import numpy as np
import pandas as pd
from scipy.stats import multinomial
# 観測度数表 (与えられたデータ)
observed_counts = np.array([[1520, 266, 124, 66],
[234, 1512, 432, 78],
[117, 362, 1772, 205],
[36, 82, 179, 492]])
# 総サンプルサイズ N の計算
N = observed_counts.sum()
# セル確率 pij の計算 (観測度数を総数で割る)
p_ij = observed_counts / N
# 観測度数とセル確率
row_labels = ["Highest", "Second", "Third", "Lowest"]
col_labels = ["Highest", "Second", "Third", "Lowest"]
# 観測度数
df_counts = pd.DataFrame(observed_counts, columns=col_labels, index=row_labels)
# セル確率
df_probs = pd.DataFrame(np.round(p_ij, 6), columns=col_labels, index=row_labels)
print("観測度数表 (x_ij):")
print(df_counts)
print("\nセル確率表 (p_ij):")
print(df_probs)
# 観測度数が得られる確率を計算
x_flat = observed_counts.flatten()
p_flat = p_ij.flatten()
# 多項分布の確率を計算
prob = multinomial.pmf(x_flat, n=N, p=p_flat)
print(f"\nこの観測度数表が得られる確率: {prob:.10e}")観測度数表 (x_ij):
Highest Second Third Lowest
Highest 1520 266 124 66
Second 234 1512 432 78
Third 117 362 1772 205
Lowest 36 82 179 492
セル確率表 (p_ij):
Highest Second Third Lowest
Highest 0.203290 0.035576 0.016584 0.008827
Second 0.031296 0.202220 0.057777 0.010432
Third 0.015648 0.048415 0.236993 0.027417
Lowest 0.004815 0.010967 0.023940 0.065802
この観測度数表が得られる確率: 7.0375704386e-24得られた確率はとても小さな数字になりました。これは、特定の具体的な度数の組み合わせが発生する確率であるため小さくなります。
2015 Q3(4)
重回帰モデルの重みの2種類の推定量のMSEを求め比較しました。

コード
![]() を
を ![]() と
と ![]() の変化に対してプロットし、その符号の変化を確認します。
の変化に対してプロットし、その符号の変化を確認します。
# 2015 Q3(4) 2024.12.16
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
r12_squared_vals = np.linspace(0, 0.99, 50) # r12^2の値(0から0.99まで)
beta2_squared_vals = np.linspace(0, 1.5, 50) # β2^2の値(0から1.5まで)
sigma2 = 1 # 誤差分散 σ^2
S11 = 10 # S11の仮定値
S12 = 5 # S12の仮定値
S22 = 15 # S22の仮定値
# グリッド生成
R12_squared, Beta2_squared = np.meshgrid(r12_squared_vals, beta2_squared_vals)
# MSEの差の計算
Var_beta2_hat = (sigma2 / S22) * (1 / (1 - R12_squared)) # Var(β2)
MSE_diff = (S12 / S11)**2 * (Var_beta2_hat - Beta2_squared) # MSEの差
# 3Dプロットの描画
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
# 3Dサーフェスプロット
surf = ax.plot_surface(R12_squared, Beta2_squared, MSE_diff, cmap='coolwarm', edgecolor='none')
# 軸ラベルとタイトル
ax.set_title(r'3Dプロット: $\mathrm{MSE}(\hat{\beta}_1) - \mathrm{MSE}(\tilde{\beta}_1)$ の符号反転', fontsize=14)
ax.set_xlabel(r'$r_{12}^2$ (相関係数の二乗)', fontsize=12)
ax.set_ylabel(r'$\beta_2^2$ (回帰係数の二乗)', fontsize=12)
ax.set_zlabel(r'$\mathrm{MSE}(\hat{\beta}_1) - \mathrm{MSE}(\tilde{\beta}_1)$', fontsize=12)
# カラーバーの追加
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=10, label='MSEの差')
plt.tight_layout()
plt.show()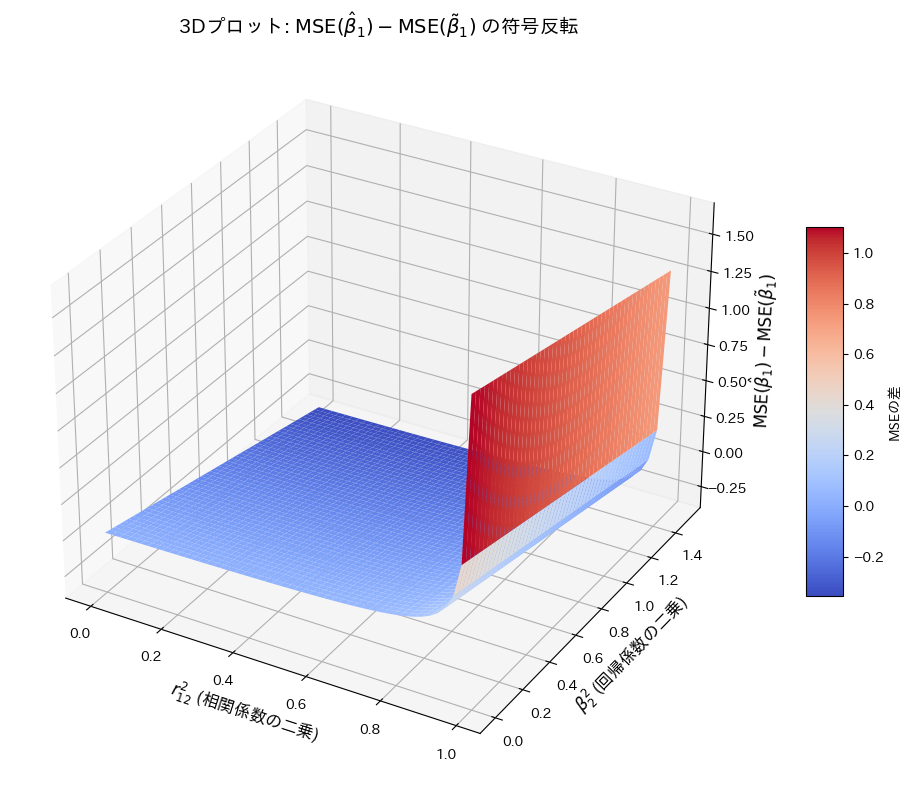
![]() の符号は
の符号は ![]() と
と ![]() の値に依存して変化することが確認できました。
の値に依存して変化することが確認できました。
2015 Q3(4)
重回帰モデルの重みの推定量の分散と、説明変数を減らした時のそれとの差を求め、説明変数間の相関係数によるどのような関数になるのか調べました。

コード
![]() の変化が
の変化が![]() と
と![]() に与える影響を、グラフで描画して確認します。
に与える影響を、グラフで描画して確認します。
# 2015 Q3(4) 2024.12.15
import numpy as np
import matplotlib.pyplot as plt
# 1. パラメータ設定
r12_vals = np.linspace(-0.99, 0.99, 200) # r12の値(-0.99から0.99まで)
sigma2 = 1 # 分散 σ^2
S11 = 10 # S11の仮定値
# 重回帰と単回帰の分散計算
Var_beta1_hat = (sigma2 / S11) * (1 / (1 - r12_vals**2)) # 重回帰(r12に依存)
Var_beta1_tilde = sigma2 / S11 # 単回帰(r12=0の分散)
# 2. グラフのプロット
plt.figure(figsize=(10, 6))
plt.plot(r12_vals, Var_beta1_hat, label=r'$\mathrm{Var}(\hat{\beta}_1)$ (重回帰)', color='blue', linewidth=2)
plt.axhline(y=Var_beta1_tilde, color='orange', linestyle='--', label=r'$\mathrm{Var}(\tilde{\beta}_1)$ (単回帰, $r_{12}=0$)')
# 軸ラベルとタイトル
plt.title(r'$\mathrm{Var}(\tilde{\beta}_1)$ と $\mathrm{Var}(\hat{\beta}_1)$ の比較', fontsize=14, fontweight='bold')
plt.xlabel(r'$r_{12}$($x_1$と$x_2$の相関)', fontsize=12)
plt.ylabel(r'分散', fontsize=12)
# 凡例とグリッド
plt.legend(fontsize=10, loc='upper right')
plt.grid(alpha=0.5)
# グラフ表示
plt.tight_layout()
plt.show()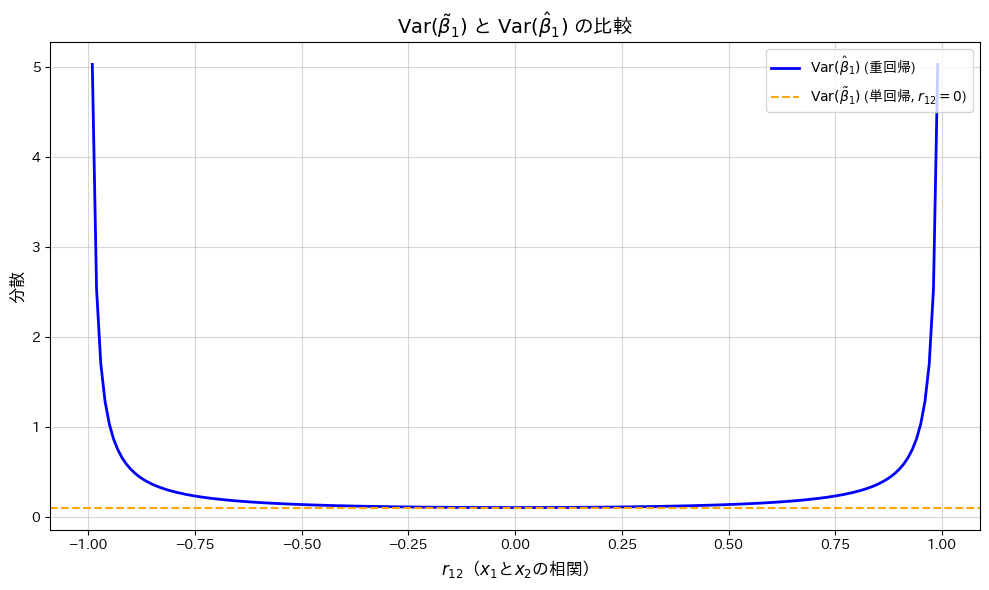
![]() が0に近いほど
が0に近いほど![]() は最小となり、相関が高まると分散が増加する一方で、
は最小となり、相関が高まると分散が増加する一方で、![]() は一定であることが確認されました。
は一定であることが確認されました。
次に、横軸を![]() として、
として、![]() と
と![]() の変化をプロットし、両者の差も併せて確認します。
の変化をプロットし、両者の差も併せて確認します。
# 2015 Q3(4) 2024.12.15
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
r12_vals = np.linspace(-0.99, 0.99, 200) # r12の値(-0.99から0.99まで)
sigma2 = 1 # 分散 σ^2
S11 = 10 # S11の仮定値
# r12^2 の計算
r12_squared_vals = r12_vals**2 # r12^2 の値
# 重回帰と単回帰の分散計算
Var_beta1_hat = (sigma2 / S11) * (1 / (1 - r12_squared_vals)) # 重回帰(r12に依存)
Var_beta1_tilde = sigma2 / S11 # 単回帰(r12=0の分散)
# 分散の差の計算
Var_diff = Var_beta1_hat - Var_beta1_tilde # 分散の差
# グラフのプロット
plt.figure(figsize=(10, 6))
# 分散のプロット
plt.plot(r12_squared_vals, Var_beta1_hat, label=r'$\mathrm{Var}(\hat{\beta}_1)$ (重回帰)', color='blue', linewidth=2)
plt.axhline(y=Var_beta1_tilde, color='orange', linestyle='--', label=r'$\mathrm{Var}(\tilde{\beta}_1)$ (単回帰, $r_{12}=0$)')
# 分散の差をプロット
plt.plot(r12_squared_vals, Var_diff, label=r'$\mathrm{Var}(\hat{\beta}_1) - \mathrm{Var}(\tilde{\beta}_1)$', color='green', linewidth=2, linestyle=':')
# 軸ラベルとタイトル
plt.title(r'$\mathrm{Var}(\tilde{\beta}_1)$, $\mathrm{Var}(\hat{\beta}_1)$ とその差の比較 ($r_{12}^2$)', fontsize=14, fontweight='bold')
plt.xlabel(r'$r_{12}^2$(相関係数の二乗)', fontsize=12)
plt.ylabel(r'分散 / 差', fontsize=12)
# 凡例とグリッド
plt.legend(fontsize=10, loc='upper right')
plt.grid(alpha=0.5)
# グラフ表示
plt.tight_layout()
plt.show()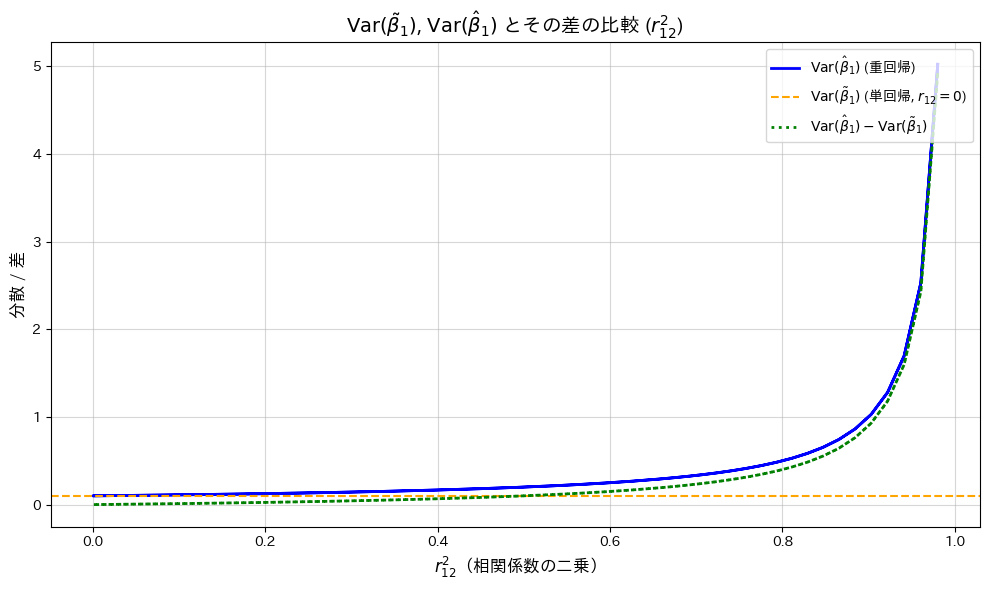
![]() が
が![]() の単調増加関数であることが確認されました。
の単調増加関数であることが確認されました。