2021 Q3(2)[2-2]
ポアソン分布に従う独立な変数の和はパラメータλの十分統計量であることを学びました。
コード
ポアソン分布に従う10個の乱数の和 Tの分布を見てみます。
# 2024 Q3(2)[2-2] 2024.8.27
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
lambda_value = 5 # 真のパラメータ
n = 10 # サンプル数
num_simulations = 1000000 # シミュレーション回数
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_value, (num_simulations, n))
# 和 T を計算
T = np.sum(samples, axis=1)
# 和 T のヒストグラムをプロット
plt.hist(T, bins=30, density=True, alpha=0.75, color='blue')
plt.title(f'Tの分布 (n 個のポアソン変数の和)')
plt.xlabel('T')
plt.ylabel('確率密度')
plt.grid(True)
plt.show()
T～Po(nλ)になっています。
つぎにT=50の条件下での確率変数X1の分布を見てます。
# 2024 Q3(2)[2-2] 2024.8.27
import numpy as np
import matplotlib.pyplot as plt
# 条件付き分布の確認
# 例えば、T = 50 の場合におけるサンプルの分布を確認
T_value = 50 # T の特定の値
samples_given_T = samples[np.sum(samples, axis=1) == T_value]
# 確率変数の1つ (X1) の分布をプロット
plt.hist(samples_given_T[:, 0], bins=15, density=True, alpha=0.75, color='green')
plt.title(f'T={T_value} の条件付き X1 の分布')
plt.xlabel('X1')
plt.ylabel('確率密度')
plt.grid(True)
plt.show()
二項分布に従っているようです。
異なるλに対して、和T=50の条件下でのX1の分布を重ねて見てます。
# 2024 Q3(2)[2-2] 2024.8.27
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
# パラメータ設定
lambda_values = [3, 5, 7] # 異なる λ の値
n = 10 # サンプル数
num_simulations = 1000000 # シミュレーション回数
T_value = 50 # T の特定の値
plt.figure(figsize=(12, 6))
for lambda_value in lambda_values:
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_value, (num_simulations, n))
# T = T_value のサンプルを抽出
samples_given_T = samples[np.sum(samples, axis=1) == T_value]
# X1 の分布をプロット
counts, bin_edges, _ = plt.hist(samples_given_T[:, 0], bins=15, density=True, alpha=0.5, label=f'λ = {lambda_value}')
# 理論二項分布を描画
x1_min, x1_max = np.min(samples_given_T[:, 0]), np.max(samples_given_T[:, 0])
x = np.arange(x1_min, x1_max + 1)
estimated_p = 1 / n # 二項分布の p は 1/n で推定
binom_pmf = binom.pmf(x, T_value, estimated_p)
plt.plot(x, binom_pmf, 'k--', label=f'理論二項分布 Bin(T={T_value}, p=1/{n})')
plt.title(f'X1の分布 (T={T_value} 条件付き) と理論二項分布')
plt.xlabel('X1')
plt.ylabel('確率密度')
plt.legend()
plt.grid(True)
plt.show()
λに依存せず同じ二項分布に従います。よって統計量Tはλに対する十分統計量であることが示されました。
なお、X1～Xnの組は多項分布に従うが、簡単のためX1のみの分布を確認しました。X1は二項分布に従います。
2021 Q3(2)[2-1]
ポアソン分布の再生性をモーメント母関数の積から示す問題をやりました。
コード
数式を使った計算
# 2021 Q3(2)[2-1] 2024.8.26
import sympy as sp
# 変数の定義
s, lambda_, n = sp.symbols('s lambda_ n', real=True, positive=True)
# 各 X_i のモーメント母関数
M_X = sp.exp(lambda_ * (sp.exp(s) - 1))
# 和 T のモーメント母関数 M_T(s)
M_T = M_X**n
# M_T(s) を簡略化
M_T_simplified = sp.simplify(M_T)
# 結果を表示
display(M_T_simplified)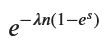
Po(nλ)のモーメント母関数に等しいです。
モーメント母関数を使って期待値と分散を求めます。
# 2021 Q3(2)[2-1] 2024.8.26
import sympy as sp
# 変数の定義
s, lambda_, n = sp.symbols('s lambda_ n', real=True, positive=True)
# モーメント母関数 M_T(s)
M_T = sp.exp(-lambda_ * n * (1 - sp.exp(s)))
# 1次モーメント（期待値）の計算
M_T_prime = sp.diff(M_T, s)
expectation = M_T_prime.subs(s, 0)
# 2次モーメントの計算
M_T_double_prime = sp.diff(M_T_prime, s)
second_moment = M_T_double_prime.subs(s, 0)
# 分散の計算
variance = second_moment - expectation**2
# 結果を表示
display(expectation, variance)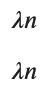
Po(nλ)の期待値と分散に一致します。