2021 Q5(2)
線形変換により得られた二つのベクトルが独立となる条件を求める問題をやりました。

コード
各行ベクトルが直交している行列LとMを生成します
# 2021 Q5(2) 2024.9.6
import numpy as np
# 乱数で4つの要素を持つ基準ベクトルを生成 (整数で0以外の値のみ)
def generate_random_integer_vector_4(n=4):
return np.random.randint(1, 10, size=n) # 1から9の範囲で整数を生成
# 生成した基準ベクトルを使って、並行するベクトルを生成
def generate_parallel_matrix_4(v, scale_factors):
L = np.array([scale * v for scale in scale_factors])
return L
# ベクトル v に直交するベクトルを生成する関数
# グラム・シュミット法を適用して、基準ベクトルに直交するベクトルを作る
def generate_orthogonal_vectors_4(v):
orthogonal_vectors = []
for _ in range(5):
candidate = np.random.randint(1, 10, size=v.shape) # 新たな候補ベクトル
# 直交条件:v と candidate の内積が 0 になるように調整
adjustment = np.dot(candidate, v) / np.dot(v, v)
orthogonal_vector = candidate - adjustment * v # 直交ベクトルにする
orthogonal_vectors.append(orthogonal_vector)
return np.array(orthogonal_vectors)
# 基準ベクトルを生成
v_base = generate_random_integer_vector_4()
# 基準ベクトルと並行するベクトルを5つ作る
scale_factors_5 = [1, 2, 3, 4, 5]
L_5x4 = generate_parallel_matrix_4(v_base, scale_factors_5)
# 基準ベクトルに直交するベクトルを5つ作る
M_5x4 = generate_orthogonal_vectors_4(v_base)
# 行列 L, M の表示とその積の確認
L_5x4, M_5x4, np.dot(L_5x4, M_5x4.T) # L, M, そしてその積を表示(array([[ 7, 1, 6, 8],
[14, 2, 12, 16],
[21, 3, 18, 24],
[28, 4, 24, 32],
[35, 5, 30, 40]]),
array([[-3.01333333, 8.42666667, -2.44 , 3.41333333],
[-1.68666667, 6.47333333, 3.84 , -2.21333333],
[ 1.28666667, 4.32666667, 0.96 , -2.38666667],
[ 1.14666667, 3.30666667, 2.84 , -3.54666667],
[-2.73333333, 4.46666667, -1.2 , 2.73333333]]),
array([[-7.10542736e-15, 7.10542736e-15, 0.00000000e+00,
-3.55271368e-15, 0.00000000e+00],
[-1.42108547e-14, 1.42108547e-14, 0.00000000e+00,
-7.10542736e-15, 0.00000000e+00],
[-2.13162821e-14, 2.13162821e-14, 7.10542736e-15,
0.00000000e+00, -7.10542736e-15],
[-2.84217094e-14, 2.84217094e-14, 0.00000000e+00,
-1.42108547e-14, 0.00000000e+00],
[-3.55271368e-14, 2.84217094e-14, 0.00000000e+00,
-2.84217094e-14, -7.10542736e-15]]))行列LとMを生成し、![]() を求めました。
を求めました。![]() はほぼゼロ行列になっています。
はほぼゼロ行列になっています。
LxとMxの共分散行列を求めます
# 2021 Q5(2) 2024.9.6
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# l, m, n を定義
l = 5 # Lの行数
m = 5 # Mの行数
n = 4 # LとMの列数 (xの次元)
# L と M を定義 (与えられた行列を使用)
L = np.array([[7, 1, 6, 8],
[14, 2, 12, 16],
[21, 3, 18, 24],
[28, 4, 24, 32],
[35, 5, 30, 40]])
M = np.array([[-3.01333333, 8.42666667, -2.44, 3.41333333],
[-1.68666667, 6.47333333, 3.84, -2.21333333],
[1.28666667, 4.32666667, 0.96, -2.38666667],
[1.14666667, 3.30666667, 2.84, -3.54666667],
[-2.73333333, 4.46666667, -1.2, 2.73333333]])
# N(0, 1) に従う乱数ベクトル x を生成 (サンプル数を10000000にする)
sample_size = 10000000
x = np.random.randn(n, sample_size)
# Lx と Mx を計算
Lx = np.dot(L, x) # lxサンプル数の行列
Mx = np.dot(M, x) # mxサンプル数の行列
# 共分散行列 Cov(Lx, Mx) を計算
cov_matrix = np.zeros((l, m))
for i in range(l):
for j in range(m):
cov_matrix[i, j] = np.cov(Lx[i, :], Mx[j, :])[0, 1]
# L * M^T の積を再計算
LM_T = np.dot(L, M.T)
# ヒートマップを描画
plt.figure(figsize=(12, 6))
# 共分散行列のヒートマップ
plt.subplot(1, 2, 1)
sns.heatmap(cov_matrix, cmap="coolwarm", annot=True, fmt=".2f", center=0, vmin=-1, vmax=1)
plt.title(f'共分散行列 Cov(Lx, Mx)')
# L * M^T のヒートマップ
plt.subplot(1, 2, 2)
sns.heatmap(LM_T, cmap="coolwarm", annot=True, fmt=".2f", center=0, vmin=-1, vmax=1)
plt.title(f'行列 L * M^T')
plt.tight_layout()
plt.show()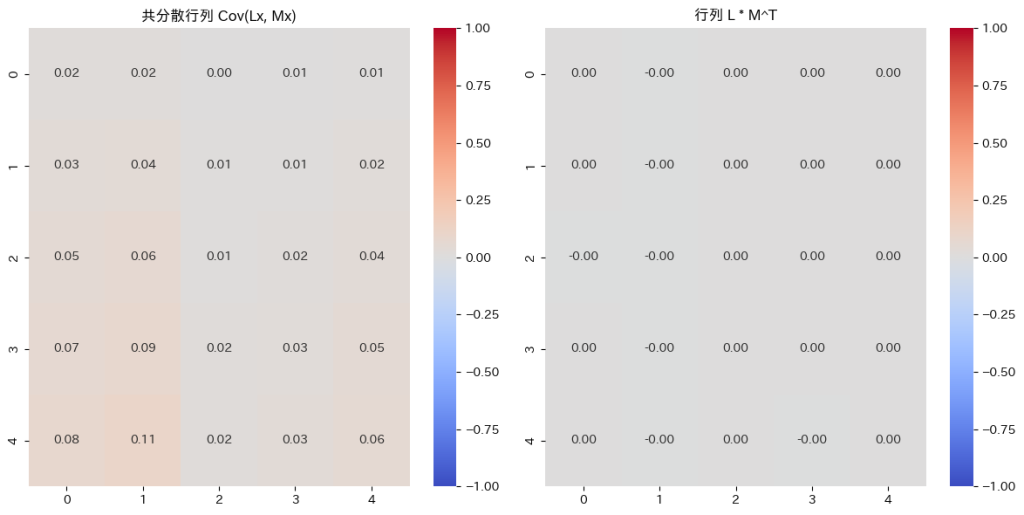
Cov(Lx,Mx)はゼロ行列に近づきます。その必要十分条件は![]() がゼロ行列になることです。
がゼロ行列になることです。
ここで注意が必要なのは、LxとMxは確率変数から成るベクトルであり、Cov(Lx,Mx)はLxとMxのそれぞれの確率変数同士の共分散を計算し、それを行列としてまとめたものです。
2021 Q5(1)
線形変換された確率変数ベクトルの分散共分散行列を求める問題をやりました。
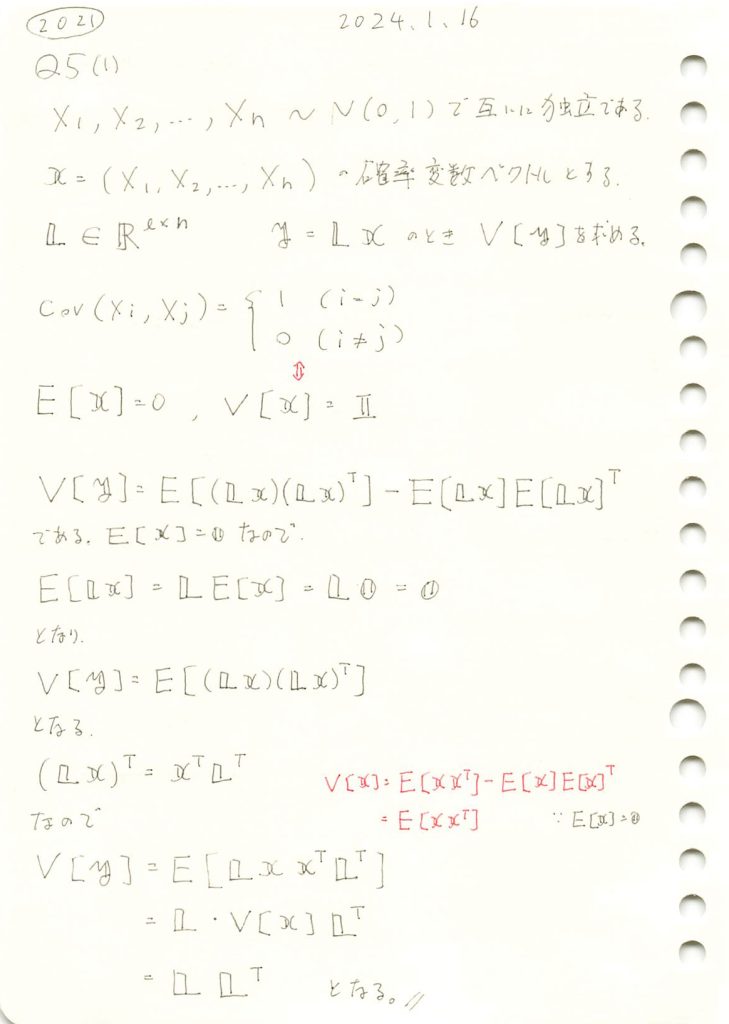
コード
シミュレーション
乱数による分散共分散行列と、![]() を比較します
を比較します
# 2021 Q5(1) 2024.9.4
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 標準正規分布からサンプルを生成
n = 1000 # サンプル数
d = 5 # 次元数
X = np.random.randn(d, n)
# 4x5の線形変換行列 L を定義
L = np.array([[9, 7, 8, 6, 5],
[6, 5, 4, 3, 2],
[3, 2, 1, 9, 8],
[8, 7, 6, 5, 0]])
# 線形変換を適用して y を計算
Y = np.dot(L, X)
# y のサンプルから分散共分散行列を推定
V_Y_estimated = np.cov(Y)
# 理論的な L・L^T と比較
V_Y_theoretical = np.dot(L, L.T)
# ヒートマップのプロット
plt.figure(figsize=(12, 6))
# 推定された分散共分散行列のヒートマップ
plt.subplot(1, 2, 1)
sns.heatmap(V_Y_estimated, annot=True, cmap="coolwarm", cbar=True)
plt.title("推定された分散共分散行列")
# 理論的な分散共分散行列のヒートマップ
plt.subplot(1, 2, 2)
sns.heatmap(V_Y_theoretical, annot=True, cmap="coolwarm", cbar=True)
plt.title("理論的な分散共分散行列")
plt.show()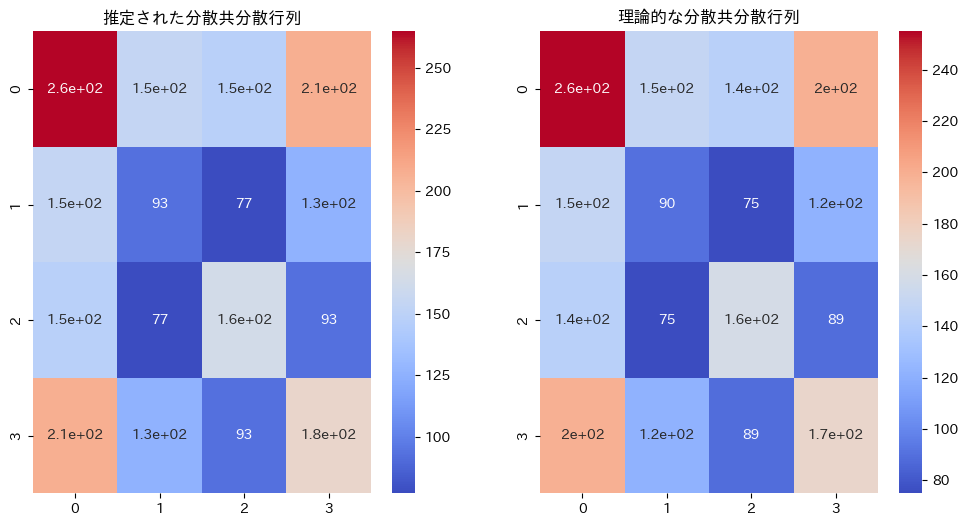
同じような行列になりました。違いは乱数によるものです。
2021 Q4(5)
τハットがτの不偏推定量になるための必要十分条件を求める問題を学びました。
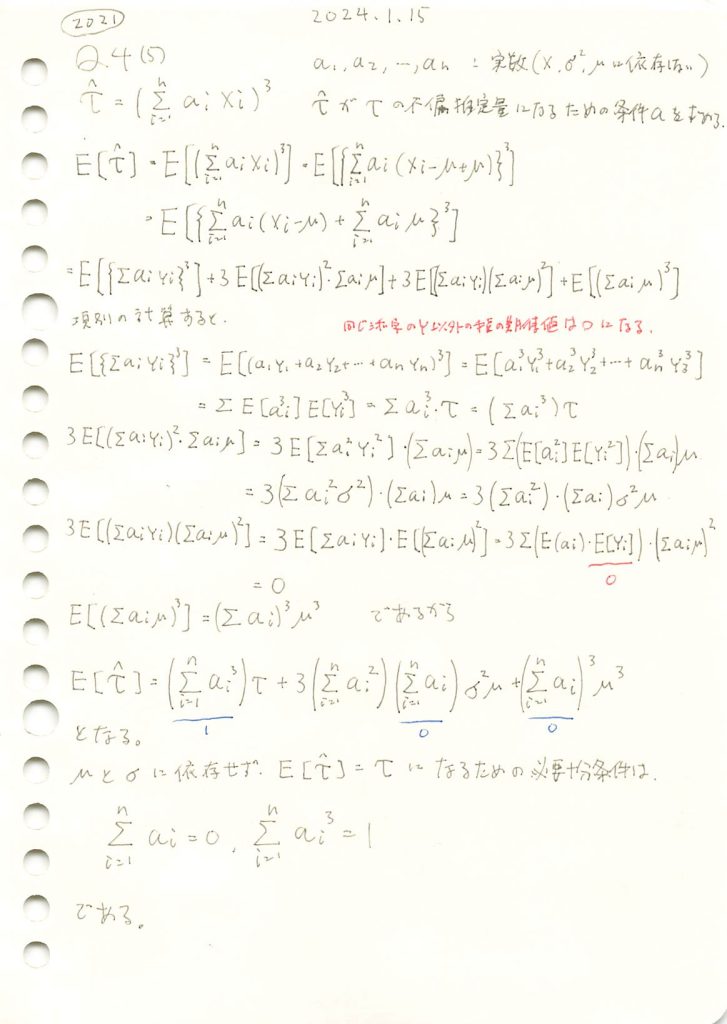
コード
![]() を満たすaiを見つける
を満たすaiを見つける
# 2021 Q4(5) 2024.9.3
import numpy as np
def find_ai_sequence(n, tolerance=1e-6):
while True:
# ランダムに n 個の値を生成
a = np.random.uniform(-1, 1, n)
# 正の数と負の数の個数を調整
neg_count = (n + 1) // 2 # 負の数を1つ多くする
pos_count = n - neg_count
a[:pos_count] = np.abs(a[:pos_count])
a[pos_count:] = -np.abs(a[pos_count:])
# 合計が0になるように調整
a -= np.mean(a)
# 条件をチェック
sum_ai = np.sum(a)
sum_ai_cubed = np.sum(a**3)
if np.abs(sum_ai) < tolerance and np.abs(sum_ai_cubed - 1) < tolerance:
return a
# パラメータの設定
n = 10 # サンプル数
# 条件を満たす a_i の数列を見つける
a = find_ai_sequence(n)
# 計算を確認
print(f"a_i の合計 (≒0): {a.sum()}")
print(f"a_i^3 の合計 (≒1): {np.sum(a ** 3)}")
# 条件を満たした a_i を表示
print("a_i の数列:")
print(a)a_i の合計 (≒0): 6.661338147750939e-16
a_i^3 の合計 (≒1): 1.0000001485058854
a_i の数列:
[ 0.13279542 1.05885499 0.24951311 0.83492921 0.13800083 -0.71178855
-0.38213634 -0.18394766 -0.55820111 -0.5780199 ]5分ほどで見つかった
見つかったaiと指数分布に従う乱数を使って![]() のシミュレーションしてみる
のシミュレーションしてみる
import numpy as np
import matplotlib.pyplot as plt
# すでに見つかった条件を満たす a_i を使用
a = np.array([ 0.13279542, 1.05885499, 0.24951311, 0.83492921, 0.13800083, -0.71178855,
-0.38213634, -0.18394766, -0.55820111, -0.5780199 ])
# パラメータの設定
n = len(a) # サンプル数(a_i の数と一致させる)
scale = 1.0 # 指数分布のスケールパラメータ
iterations = 10000 # シミュレーション回数
# シミュレーション結果を保存するリスト
tau_hat_values = []
# シミュレーションを実行
for _ in range(iterations):
# 指数分布に従う乱数を生成
X = np.random.exponential(scale=scale, size=n)
# \hat{\tau} の計算
tau_hat = np.sum(a * X) ** 3
tau_hat_values.append(tau_hat)
# 指数分布の三次中心モーメントを計算
tau = 2 * scale**3 # 指数分布における三次中心モーメント
# シミュレーション結果の平均
simulated_mean_tau_hat = np.mean(tau_hat_values)
# 結果を表示
print(f"理論値の τ: {tau}")
print(f"シミュレーションによる τ の推定値: {simulated_mean_tau_hat}")
# 視覚化
plt.figure(figsize=(10, 6))
plt.hist(tau_hat_values, bins=50, alpha=0.75, label='シミュレーション結果')
plt.axvline(simulated_mean_tau_hat, color='red', linestyle='dashed', linewidth=2, label=f'シミュレーション平均 = {simulated_mean_tau_hat:.2f}')
plt.axvline(tau, color='blue', linestyle='dashed', linewidth=2, label=f'理論値 = {tau:.2f}')
plt.xlabel('値')
plt.ylabel('頻度')
plt.title(r"$\hat{\tau} = \left(\sum_{i=1}^{n} a_i X_i\right)^3$ の分布 (指数分布)")
plt.legend()
plt.grid(True)
plt.show()理論値の τ: 2.0
シミュレーションによる τ の推定値: 2.0555706049874143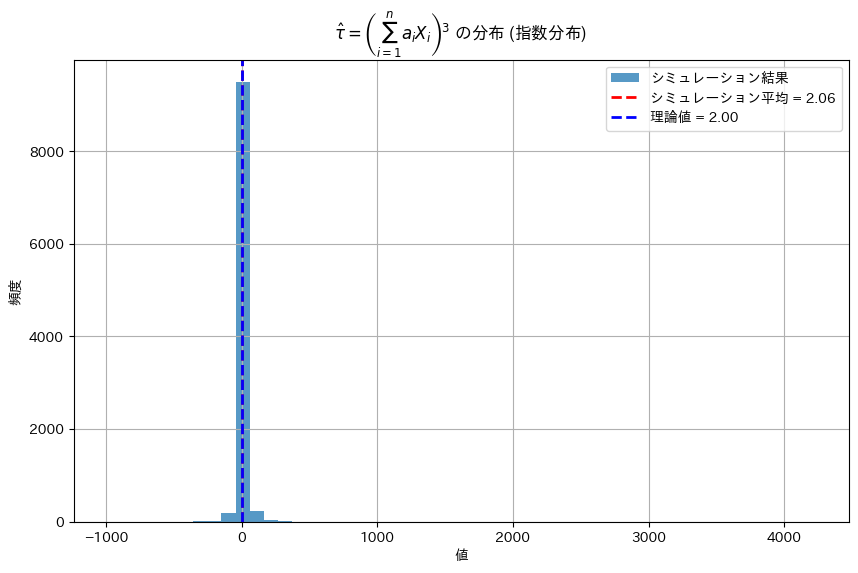
推定値は理論値と近い値をとった。ただし1.5~2.5付近で値が変動する。原因として、n=10が小さい、三次であるから乱数のばらつきに敏感、指数分布は大きな値をとる、が挙げられる。
2021 Q4(4)
標本平均との差の3乗の和の期待値を求める問題をやりました。
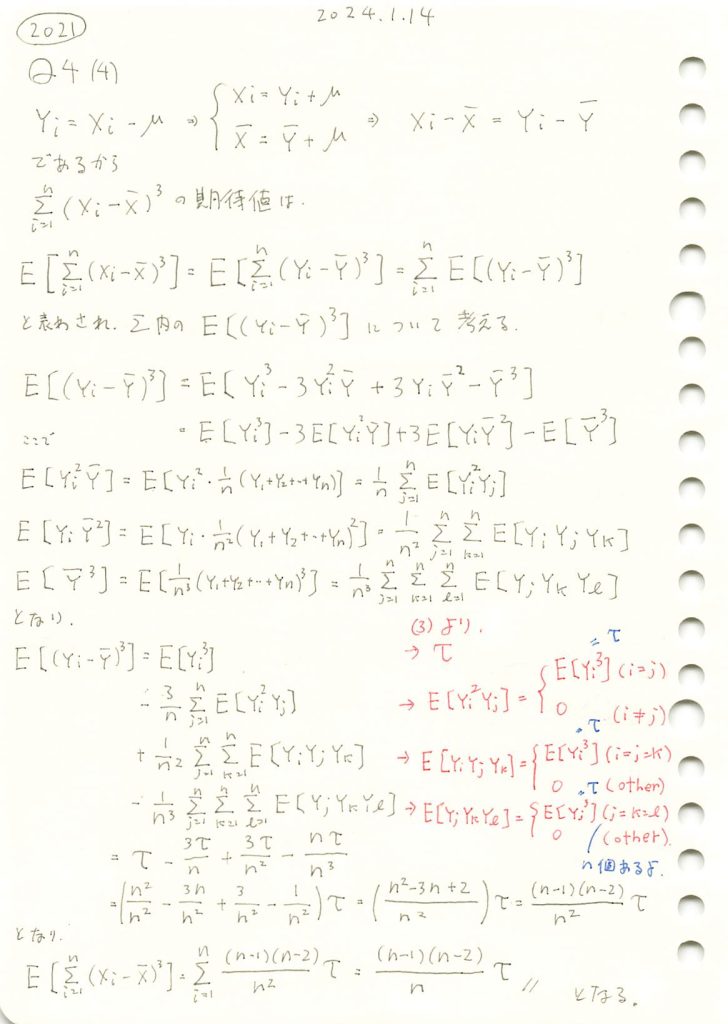
コード
シミュレーションをして理論値と比較します
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
n = 10 # サンプル数 (必要に応じて変更可能)
scale = 1.0 # 指数分布のスケールパラメータ(1/λ)
iterations = 10000 # シミュレーション回数
# シミュレーション結果を保存するリスト
sum_X_i_minus_X_bar_cubed_values = []
# シミュレーションを実行
for _ in range(iterations):
# 指数分布に従う乱数を生成
X = np.random.exponential(scale=scale, size=n)
# 標本平均を計算
X_bar = np.mean(X)
# (X_i - X_bar)^3 の合計を計算
sum_X_i_minus_X_bar_cubed = np.sum((X - X_bar)**3)
sum_X_i_minus_X_bar_cubed_values.append(sum_X_i_minus_X_bar_cubed)
# 指数分布の三次中心モーメントを計算
tau = 2 * scale**3 # 指数分布における三次中心モーメント
# 理論値の計算
theoretical_value = (n - 1) * (n - 2) * tau / n
# シミュレーション結果の平均
simulated_mean = np.mean(sum_X_i_minus_X_bar_cubed_values)
# 結果を表示
print(f"理論値: {theoretical_value}")
print(f"シミュレーションによる平均: {simulated_mean}")
# 視覚化
plt.figure(figsize=(10, 6))
plt.hist(sum_X_i_minus_X_bar_cubed_values, bins=50, alpha=0.75, label='シミュレーション結果')
plt.axvline(simulated_mean, color='red', linestyle='dashed', linewidth=2, label=f'シミュレーション平均 = {simulated_mean:.2f}')
plt.axvline(theoretical_value, color='blue', linestyle='dashed', linewidth=2, label=f'理論値 = {theoretical_value:.2f}')
plt.xlabel('値')
plt.ylabel('頻度')
plt.title(r"$\sum_{i=1}^{n} (X_i - \overline{X})^3$ の分布 (指数分布)")
plt.legend()
plt.grid(True)
plt.show()理論値: 14.4
シミュレーションによる平均: 14.499748799877718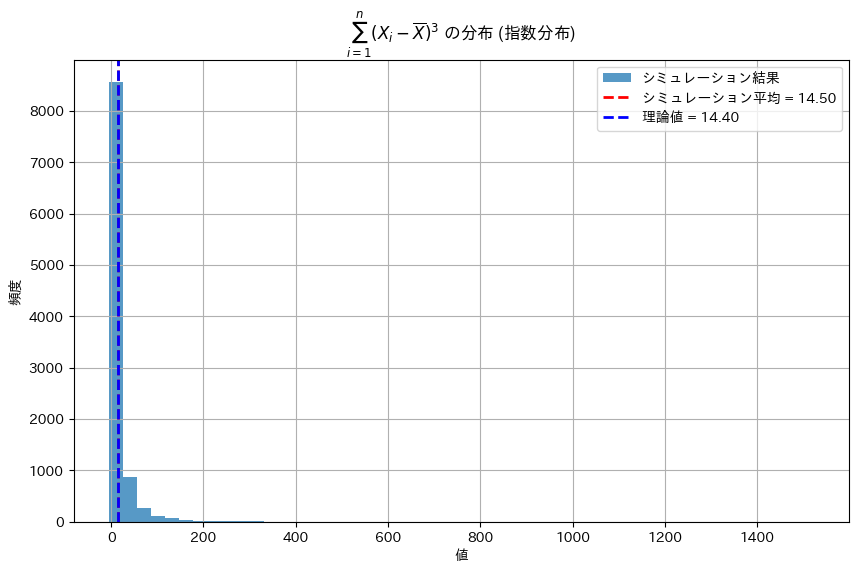
シミュレーションは理論値に近い値を示しました
コード中の三次中心モーメントの導出を下記に示します
指数分布の三次中心モーメント (=τ) の導出
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2021 Q4(3)
確率変数と母平均の差に関する期待値の計算をしました。
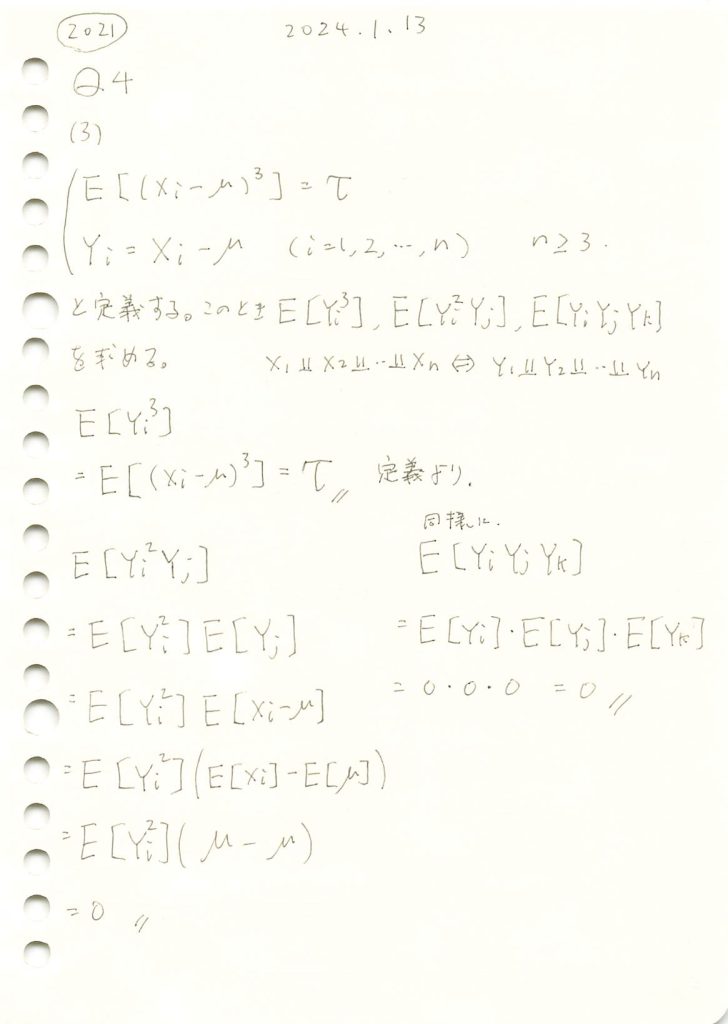
コード
Xiが正規分布(μ=0, σ=1)に従う場合
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
n = 1000 # サンプル数
mu, sigma = 0, 1 # 正規分布の平均と標準偏差
iterations = 10000 # シミュレーション回数
# シミュレーション結果を保存するリスト
Y_i_cubed_values = []
Y_i_squared_Y_j_values = []
Y_i_Y_j_Y_k_values = []
# シミュレーションを実行
for _ in range(iterations):
X_i = np.random.normal(mu, sigma, size=n)
X_j = np.random.normal(mu, sigma, size=n)
X_k = np.random.normal(mu, sigma, size=n)
Y_i = X_i - mu
Y_j = X_j - mu
Y_k = X_k - mu
Y_i_cubed_values.append(np.mean(Y_i**3))
Y_i_squared_Y_j_values.append(np.mean(Y_i**2 * Y_j))
Y_i_Y_j_Y_k_values.append(np.mean(Y_i * Y_j * Y_k))
# グラフを横に並べて表示
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# (1) E[Y_i^3] の分布
axes[0].hist(Y_i_cubed_values, bins=50, alpha=0.75)
axes[0].axvline(np.mean(Y_i_cubed_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[0].set_title(r"正規分布における $E[Y_i^3]$ の分布")
axes[0].set_xlabel('値')
axes[0].set_ylabel('頻度')
axes[0].legend()
# (2) E[Y_i^2 Y_j] の分布
axes[1].hist(Y_i_squared_Y_j_values, bins=50, alpha=0.75)
axes[1].axvline(np.mean(Y_i_squared_Y_j_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[1].set_title(r"正規分布における $E[Y_i^2 Y_j]$ の分布")
axes[1].set_xlabel('値')
axes[1].set_ylabel('頻度')
axes[1].legend()
# (3) E[Y_i Y_j Y_k] の分布
axes[2].hist(Y_i_Y_j_Y_k_values, bins=50, alpha=0.75)
axes[2].axvline(np.mean(Y_i_Y_j_Y_k_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[2].set_title(r"正規分布における $E[Y_i Y_j Y_k]$ の分布")
axes[2].set_xlabel('値')
axes[2].set_ylabel('頻度')
axes[2].legend()
# グラフを表示
plt.tight_layout()
plt.show()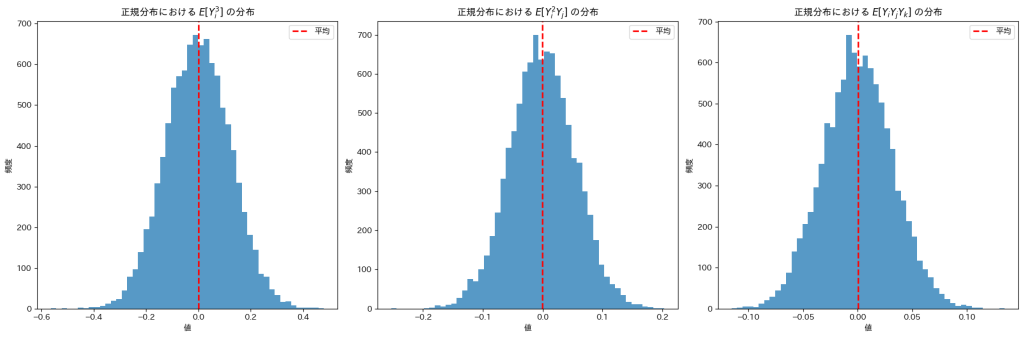
![]() は0になります
は0になります
Xiが指数分布(λ=1)に従う場合
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
n = 1000 # サンプル数
scale = 1.0 # 指数分布のスケールパラメータ(1/λ)
iterations = 10000 # シミュレーション回数
# シミュレーション結果を保存するリスト
Y_i_cubed_values = []
Y_i_squared_Y_j_values = []
Y_i_Y_j_Y_k_values = []
# シミュレーションを実行
for _ in range(iterations):
X_i = np.random.exponential(scale=scale, size=n)
X_j = np.random.exponential(scale=scale, size=n)
X_k = np.random.exponential(scale=scale, size=n)
Y_i = X_i - np.mean(X_i)
Y_j = X_j - np.mean(X_j)
Y_k = X_k - np.mean(X_k)
Y_i_cubed_values.append(np.mean(Y_i**3))
Y_i_squared_Y_j_values.append(np.mean(Y_i**2 * Y_j))
Y_i_Y_j_Y_k_values.append(np.mean(Y_i * Y_j * Y_k))
# グラフを横に並べて表示
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# (1) E[Y_i^3] の分布
axes[0].hist(Y_i_cubed_values, bins=50, alpha=0.75)
axes[0].axvline(np.mean(Y_i_cubed_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[0].set_title(r"指数分布における $E[Y_i^3]$ の分布")
axes[0].set_xlabel('値')
axes[0].set_ylabel('頻度')
axes[0].legend()
# (2) E[Y_i^2 Y_j] の分布
axes[1].hist(Y_i_squared_Y_j_values, bins=50, alpha=0.75)
axes[1].axvline(np.mean(Y_i_squared_Y_j_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[1].set_title(r"指数分布における $E[Y_i^2 Y_j]$ の分布")
axes[1].set_xlabel('値')
axes[1].set_ylabel('頻度')
axes[1].legend()
# (3) E[Y_i Y_j Y_k] の分布
axes[2].hist(Y_i_Y_j_Y_k_values, bins=50, alpha=0.75)
axes[2].axvline(np.mean(Y_i_Y_j_Y_k_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[2].set_title(r"指数分布における $E[Y_i Y_j Y_k]$ の分布")
axes[2].set_xlabel('値')
axes[2].set_ylabel('頻度')
axes[2].legend()
# グラフを表示
plt.tight_layout()
plt.show()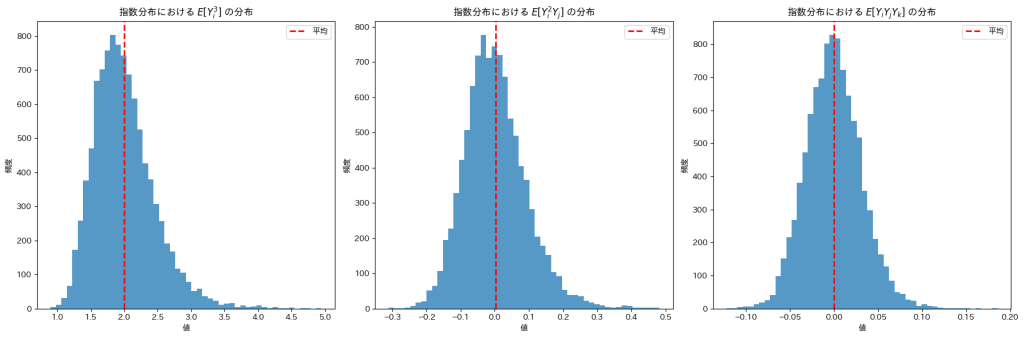
![]() は0になりますが、
は0になりますが、![]() は2付近の値をとっているようです。
は2付近の値をとっているようです。
Xiがガンマ分布(形状パラメータ=2, スケールパラメータ=2)に従う場合
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
n = 1000 # サンプル数
shape, scale = 2.0, 2.0 # ガンマ分布の形状パラメータとスケールパラメータ
iterations = 10000 # シミュレーション回数
# シミュレーション結果を保存するリスト
Y_i_cubed_values = []
Y_i_squared_Y_j_values = []
Y_i_Y_j_Y_k_values = []
# シミュレーションを実行
for _ in range(iterations):
X_i = np.random.gamma(shape, scale, size=n)
X_j = np.random.gamma(shape, scale, size=n)
X_k = np.random.gamma(shape, scale, size=n)
Y_i = X_i - np.mean(X_i)
Y_j = X_j - np.mean(X_j)
Y_k = X_k - np.mean(X_k)
Y_i_cubed_values.append(np.mean(Y_i**3))
Y_i_squared_Y_j_values.append(np.mean(Y_i**2 * Y_j))
Y_i_Y_j_Y_k_values.append(np.mean(Y_i * Y_j * Y_k))
# グラフを横に並べて表示
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# (1) E[Y_i^3] の分布
axes[0].hist(Y_i_cubed_values, bins=50, alpha=0.75)
axes[0].axvline(np.mean(Y_i_cubed_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[0].set_title(r"ガンマ分布における $E[Y_i^3]$ の分布")
axes[0].set_xlabel('値')
axes[0].set_ylabel('頻度')
axes[0].legend()
# (2) E[Y_i^2 Y_j] の分布
axes[1].hist(Y_i_squared_Y_j_values, bins=50, alpha=0.75)
axes[1].axvline(np.mean(Y_i_squared_Y_j_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[1].set_title(r"ガンマ分布における $E[Y_i^2 Y_j]$ の分布")
axes[1].set_xlabel('値')
axes[1].set_ylabel('頻度')
axes[1].legend()
# (3) E[Y_i Y_j Y_k] の分布
axes[2].hist(Y_i_Y_j_Y_k_values, bins=50, alpha=0.75)
axes[2].axvline(np.mean(Y_i_Y_j_Y_k_values), color='red', linestyle='dashed', linewidth=2, label='平均')
axes[2].set_title(r"ガンマ分布における $E[Y_i Y_j Y_k]$ の分布")
axes[2].set_xlabel('値')
axes[2].set_ylabel('頻度')
axes[2].legend()
# グラフを表示
plt.tight_layout()
plt.show()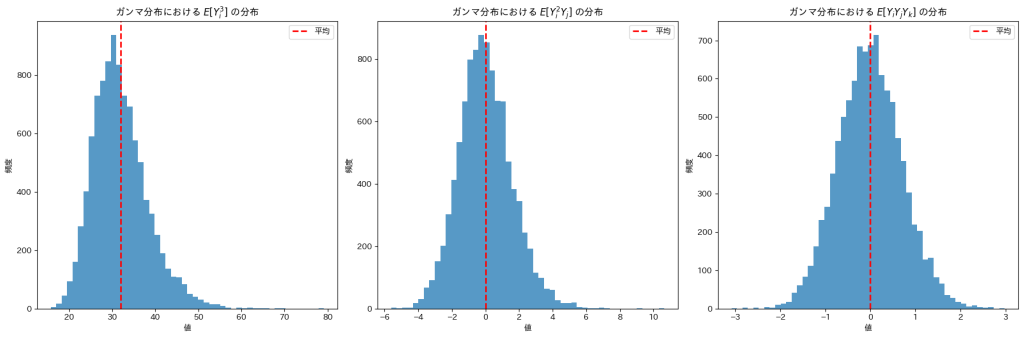
![]() は0になりますが、
は0になりますが、![]() は32付近の値をとっているようです。
は32付近の値をとっているようです。
2021 Q4(1)(2)
平均の分散と、同じ分布に従う2変数の差の3乗の期待値を求めました。

(1)標本平均の分散
# 2021 Q4(1) 2024.8.31
import numpy as np
# パラメータの設定
n = 100 # サンプル数
mu = 0 # 平均
sigma = 1 # 標準偏差
iterations = 10000 # シミュレーション回数
# 各シミュレーションで得た標本平均を格納するリスト
sample_means = []
for _ in range(iterations):
# 正規分布に従う乱数を生成
X = np.random.normal(loc=mu, scale=sigma, size=n)
# 標本平均を計算
X_bar = np.mean(X)
sample_means.append(X_bar)
# 標本平均の分散を計算
estimated_variance_of_sample_mean = np.var(sample_means)
# 理論的な分散
theoretical_variance = sigma**2 / n
print(f"理論的な分散: {theoretical_variance}")
print(f"推定された標本平均の分散: {estimated_variance_of_sample_mean}")
理論的な分散: 0.01
推定された標本平均の分散: 0.009838287336429174分布を見てみます
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
n = 100 # サンプル数
mu = 0 # 平均
sigma = 1 # 標準偏差
iterations = 10000 # シミュレーション回数
# 分散の推定値を格納するリスト
estimated_variances = []
for _ in range(iterations):
# 正規分布に従う乱数を生成
X = np.random.normal(loc=mu, scale=sigma, size=n)
# 標本平均の分散を計算
estimated_variance = np.var(X) / n
estimated_variances.append(estimated_variance)
# 理論的な分散
theoretical_variance = sigma**2 / n
# 視覚化
plt.figure(figsize=(10, 6))
plt.hist(estimated_variances, bins=100, alpha=0.75, label='推定された分散', range=(0.005, 0.015))
plt.axvline(theoretical_variance, color='red', linestyle='dashed', linewidth=2, label=f'理論的な分散 = {theoretical_variance}')
plt.xlabel('分散')
plt.ylabel('頻度')
plt.title(f'{iterations}回のシミュレーションにおける推定された分散の分布\n(サンプルサイズ = {n})')
plt.legend()
plt.grid(True)
plt.show()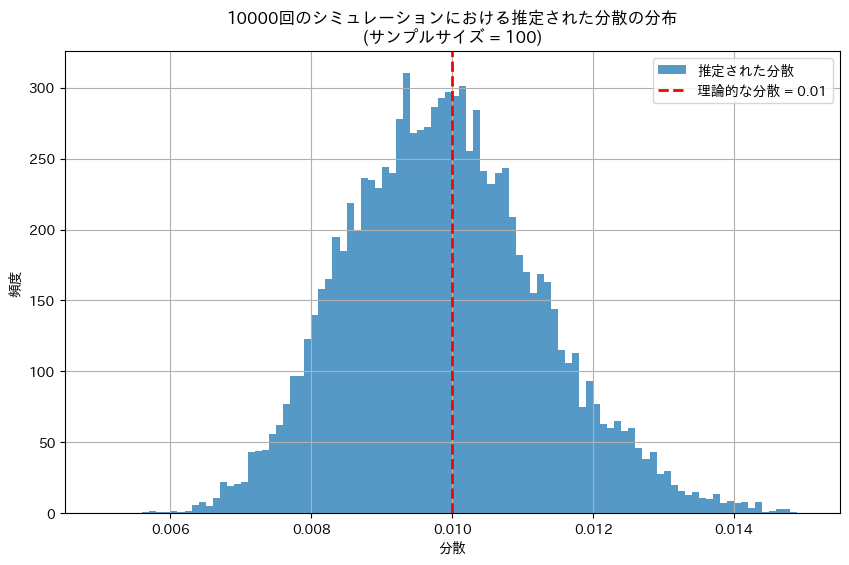
(2) 2変数の差の3乗の期待値
# 2021 Q4(1) 2024.8.31
import numpy as np
# パラメータの設定
n_simulations = 10000 # シミュレーション回数
mu = 0 # 平均
sigma = 1 # 標準偏差
# X1, X2を正規分布から生成
X1 = np.random.normal(loc=mu, scale=sigma, size=n_simulations)
X2 = np.random.normal(loc=mu, scale=sigma, size=n_simulations)
# (X1 - X2)^3を計算
expression = (X1 - X2)**3
# 期待値を計算
expected_value = np.mean(expression)
print(f"(X1 - X2)^3 の期待値: {expected_value}")(X1 - X2)^3 の期待値: 0.044962030052379295分布を見てみます
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
n = 10000 # シミュレーション回数
mu = 0 # 平均
sigma = 1 # 標準偏差
# (X1 - X2)^3 の推定値を格納するリスト
expected_values = []
for _ in range(n):
# 正規分布に従う X1, X2 を生成
X1 = np.random.normal(loc=mu, scale=sigma)
X2 = np.random.normal(loc=mu, scale=sigma)
# (X1 - X2)^3 を計算
value = (X1 - X2)**3
expected_values.append(value)
# 理論的な期待値
theoretical_expectation = 0
# 視覚化
plt.figure(figsize=(10, 6))
plt.hist(expected_values, bins=100, alpha=0.75, label='(X1 - X2)^3 の推定値', range=(-30, 30))
plt.axvline(theoretical_expectation, color='red', linestyle='dashed', linewidth=2, label=f'理論的な期待値 = {theoretical_expectation}')
plt.xlabel('値')
plt.ylabel('頻度')
plt.title(f'{n}回のシミュレーションにおける (X1 - X2)^3 の期待値の分布')
plt.legend()
plt.grid(True)
plt.show()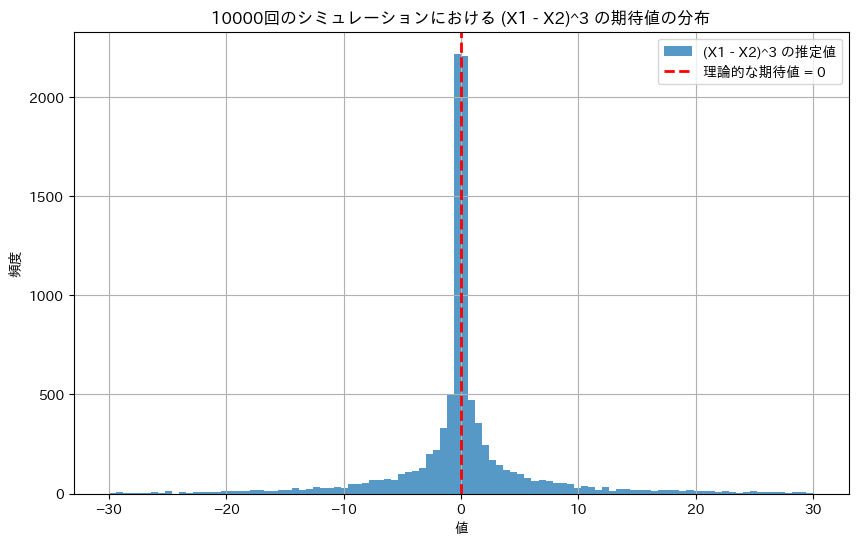
|X1-X2|が1より小さい場合は0付近に集中し、|X1-X2|が1より大きい場合は、三乗によって値が急激に増減する。分布は中心が尖って、左右対称になる。外れ値の影響を受けやすい。
2021 Q3(4)
ポアソン分布のパラメータλの区間推定の中点がその最尤推定値より大きくなることを学びました。面白い。

コード
ポアソン分布の確率質量関数にλに3,5,10を与えてプロットします
#2021 Q3(4) 2024.8.30
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# パラメータ設定
lambda_values = [3, 5, 10] # 異なる λ の値
max_x = 25 # x軸の最大値(PMFの表示範囲)
# プロットの設定
plt.figure(figsize=(12, 6))
# 各 λ について PMF を計算し、プロット
for lambda_value in lambda_values:
x = np.arange(0, max_x + 1) # x軸の範囲
pmf = poisson.pmf(x, lambda_value) # PMF を計算
plt.plot(x, pmf, marker='o', label=f'λ = {lambda_value}')
# グラフの装飾
plt.title('ポアソン分布の確率質量関数(PMF)の比較')
plt.xlabel('x')
plt.ylabel('P(X=x)')
plt.legend()
plt.grid(True)
plt.show()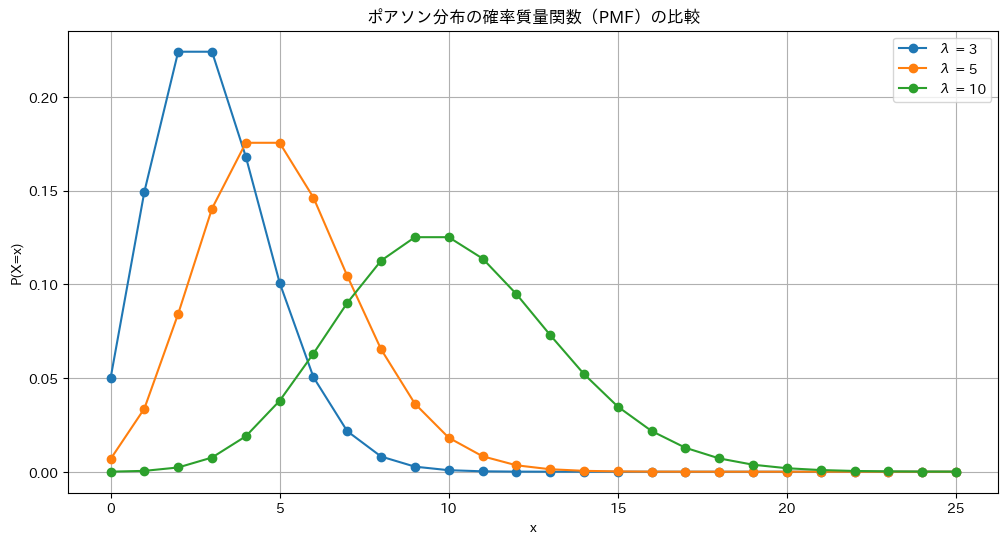
λが大きくなるほど分散も大きくなります
λの信頼区間と最尤推定値の関係を見てみます
#2021 Q3(4) 2024.8.30
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
lambda_true = 5 # 真の λ の値
n = 10 # サンプル数
num_simulations = 1000 # シミュレーション回数
# 信頼区間と最尤推定値の保存リスト
lambda_L_values = []
lambda_U_values = []
lambda_hat_values = []
# シミュレーション開始
for _ in range(num_simulations):
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_true, n)
T = np.sum(samples) # T を計算
# 最尤推定値を計算
lambda_hat = T / n
# 信頼区間の計算
lambda_L = (T - 2*np.sqrt(T + 1) + 2) / n
lambda_U = (T + 2*np.sqrt(T + 1) + 2) / n
# 結果を保存
lambda_L_values.append(lambda_L)
lambda_U_values.append(lambda_U)
lambda_hat_values.append(lambda_hat)
# 信頼区間の中点の計算
lambda_M_values = [(lambda_L_values[i] + lambda_U_values[i]) / 2 for i in range(num_simulations)]
lambda_M_mean = np.mean(lambda_M_values)
# 最尤推定値の平均を計算
lambda_hat_mean = np.mean(lambda_hat_values)
# 信頼区間のプロット
plt.figure(figsize=(12, 6))
for i in range(num_simulations):
plt.plot([lambda_L_values[i], lambda_U_values[i]], [i, i], color='blue')
plt.axvline(lambda_hat_mean, color='purple', linestyle='--', label='最尤推定値の平均')
plt.axvline(lambda_M_mean, color='orange', linestyle='-', label='信頼区間の中点の平均')
plt.title('信頼区間と最尤推定値の関係')
plt.xlabel('λ の値')
plt.ylabel('シミュレーション回数')
plt.legend()
plt.grid(True)
plt.show()
# 中点の平均値を表示
print(f'信頼区間の中点の平均: {lambda_M_mean:.4f}')
print(f'最尤推定値の平均: {lambda_hat_mean:.4f}')
print(f'真の λ: {lambda_true}')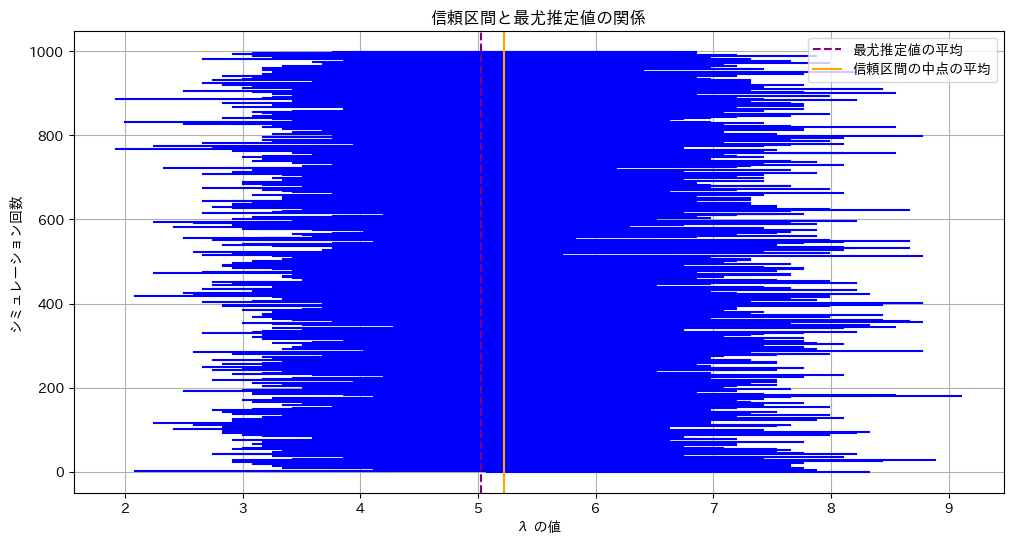
信頼区間の中点の平均: 5.2235
最尤推定値の平均: 5.0235
真の λ: 5λの信頼区間の中点は最尤推定値よりも右にずれます。λが大きくなると分散が大きくなるためです。
X=5に固定したポアソン分布の確率質量関数P(X=5|λ)のグラフを見てみます
#2021 Q3(4) 2024.8.30
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
# パラメータ設定
x_value = 5 # 固定された x の値
n = 10 # サンプル数(ここでは仮に10個の観測データがあると仮定)
T = x_value * n # 合計値 T は x * n として計算
# λの範囲を指定
lambda_range = np.linspace(1, 20, 200)
# λに対するPMFを計算
pmf_values = poisson.pmf(x_value, lambda_range)
# 最尤推定値(λ_hat)を計算
lambda_hat = T / n
# 信頼区間の計算
lambda_L = (T - 2*np.sqrt(T + 1) + 2) / n
lambda_U = (T + 2*np.sqrt(T + 1) + 2) / n
lambda_M = (lambda_L + lambda_U) / 2 # 信頼区間の中点
# グラフの描画
plt.figure(figsize=(12, 6))
plt.plot(lambda_range, pmf_values, label=f'P(X={x_value})')
# 最尤推定値、信頼区間の上下限、中点を表示
plt.axvline(lambda_hat, color='red', linestyle='--', label=f'最尤推定値 λ_hat = {lambda_hat:.2f}')
plt.axvline(lambda_L, color='blue', linestyle='--', label=f'信頼区間下限 λ_L = {lambda_L:.2f}')
plt.axvline(lambda_U, color='green', linestyle='--', label=f'信頼区間上限 λ_U = {lambda_U:.2f}')
plt.axvline(lambda_M, color='orange', linestyle='-', label=f'信頼区間中点 λ_M = {lambda_M:.2f}')
# グラフの装飾
plt.title(f'ポアソン分布のPMFと信頼区間の中点(x={x_value}固定)')
plt.xlabel('λ')
plt.ylabel(f'P(X={x_value})')
plt.grid(True)
plt.legend()
plt.show()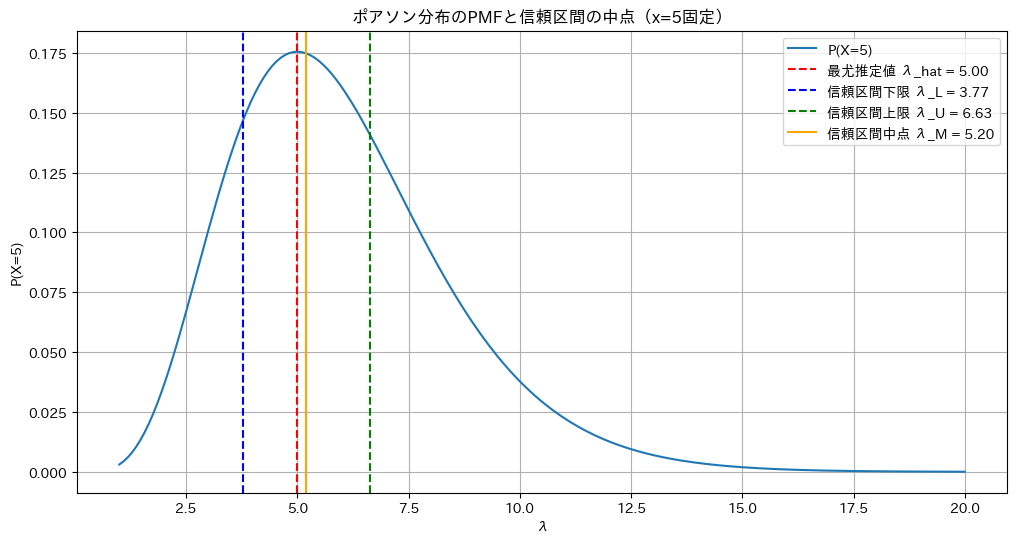
右に裾が長く、λの信頼区間の中点は最尤推定値よりも右にズレていることが分かります。
なお、このグラフは、ボソン分布の確率質量関数
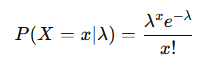
より
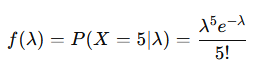
となります。これは、k=6 , θ=1 としたときガンマ分布に一致します
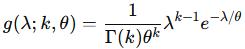
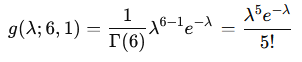
2021 Q3(3)
ポアソン分布に従う複数の確率変数の和が正規分布に近似するとした場合の信頼区間を求める問題を学びました。
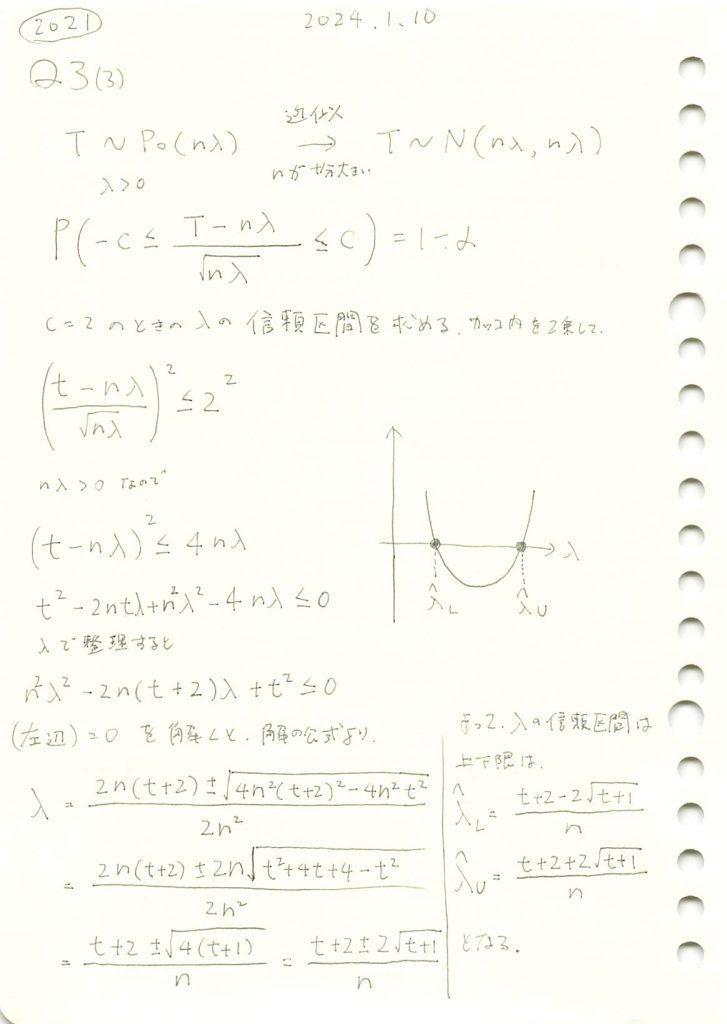
コード
二次方程式を解いて信頼区間を求めます
# 2021 Q3(3) 2024.8.29
import sympy as sp
# 変数の定義
n, lambda_, T = sp.symbols('n lambda_ T', real=True, positive=True)
c = 2
# 不等式を通常の方程式として変換
# まず、二次方程式の形を導出
lhs = sp.Eq((T - n*lambda_)**2, (c**2) * n * lambda_)
# λに関する二次方程式を解く
solutions = sp.solve(lhs, lambda_)
# 解の表示
lambda_L = solutions[0].simplify()
lambda_U = solutions[1].simplify()
# 結果の表示
display(lambda_L, lambda_U)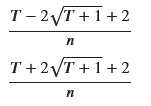
シミュレーションで、真のλが信頼区間に含まれる割合を求めます
# 2021 Q3(3) 2024.8.29
import numpy as np
# パラメータの設定
lambda_true = 5 # 真の λ の値
n = 10 # サンプル数
num_simulations = 1000 # シミュレーションの回数
# 結果を保存するカウンター
within_confidence = 0
# シミュレーション開始
for _ in range(num_simulations):
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_true, n)
T = np.sum(samples) # T を計算
# 信頼区間の計算
lambda_L = (T - 2*np.sqrt(T + 1) + 2) / n
lambda_U = (T + 2*np.sqrt(T + 1) + 2) / n
# 真のλが信頼区間内にあるか確認
if lambda_L <= lambda_true <= lambda_U:
within_confidence += 1
# 信頼区間内に真のλが含まれる割合を計算
coverage = within_confidence / num_simulations
# 結果の表示
print(f"{num_simulations}回のシミュレーションのうち、真のλが信頼区間内に含まれていた割合: {coverage:.4f}")1000回のシミュレーションのうち、真のλが信頼区間内に含まれていた割合: 0.9550c=2のとき信頼区間の信頼率は95.45%となり、シミュレーションと概ね一致します
上のシミュレーションを視覚化します
# 2021 Q3(3) 2024.8.29
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
lambda_true = 5 # 真の λ の値
n = 10 # サンプル数
num_simulations = 1000 # シミュレーションの回数
# 結果を保存するリスト
lower_limits = []
upper_limits = []
within_confidence = 0
# シミュレーション開始
for _ in range(num_simulations):
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_true, n)
T = np.sum(samples) # T を計算
# 信頼区間の計算
lambda_L = (T - 2*np.sqrt(T + 1) + 2) / n
lambda_U = (T + 2*np.sqrt(T + 1) + 2) / n
# 信頼区間の記録
lower_limits.append(lambda_L)
upper_limits.append(lambda_U)
# 真のλが信頼区間内にあるか確認
if lambda_L <= lambda_true <= lambda_U:
within_confidence += 1
# 信頼区間内に真のλが含まれる割合を計算
coverage = within_confidence / num_simulations
print(f"{num_simulations}回のシミュレーションのうち、真のλが信頼区間内に含まれていた割合: {coverage:.4f}")
# ヒストグラムのプロット
plt.figure(figsize=(12, 6))
plt.hist(lower_limits, bins=30, alpha=0.5, label='信頼区間の下限', color='blue')
plt.hist(upper_limits, bins=30, alpha=0.5, label='信頼区間の上限', color='red')
plt.axvline(lambda_true, color='green', linestyle='--', label='真の λ')
plt.title('信頼区間の分布')
plt.xlabel('λ の値')
plt.ylabel('頻度')
plt.legend()
plt.grid(True)
plt.show()
# 信頼区間のプロット
plt.figure(figsize=(12, 6))
for i in range(num_simulations):
plt.plot([lower_limits[i], upper_limits[i]], [i, i], color='blue')
plt.axvline(lambda_true, color='red', linestyle='--', label='真の λ')
plt.title('シミュレーションごとの信頼区間')
plt.xlabel('λ の値')
plt.ylabel('シミュレーション回数')
plt.legend()
plt.grid(True)
plt.show()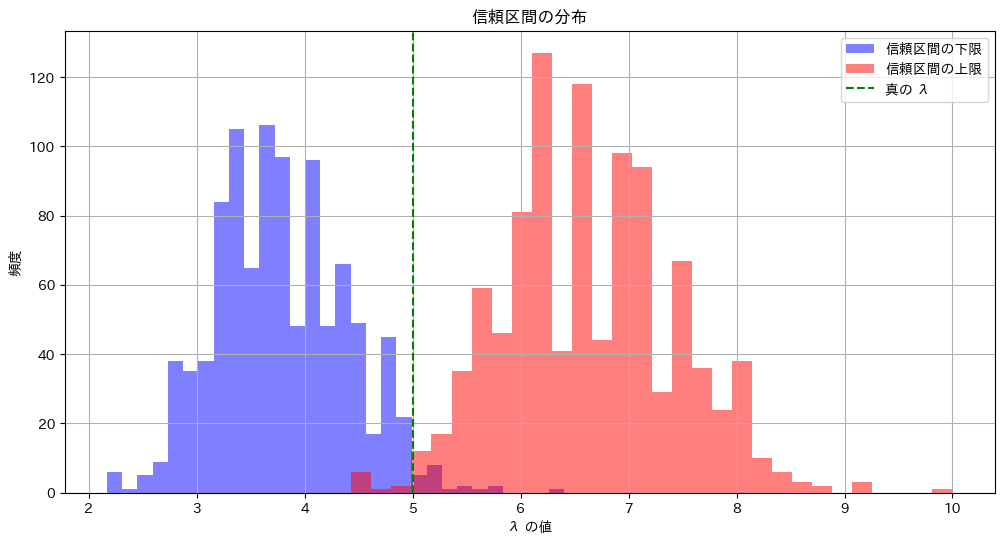
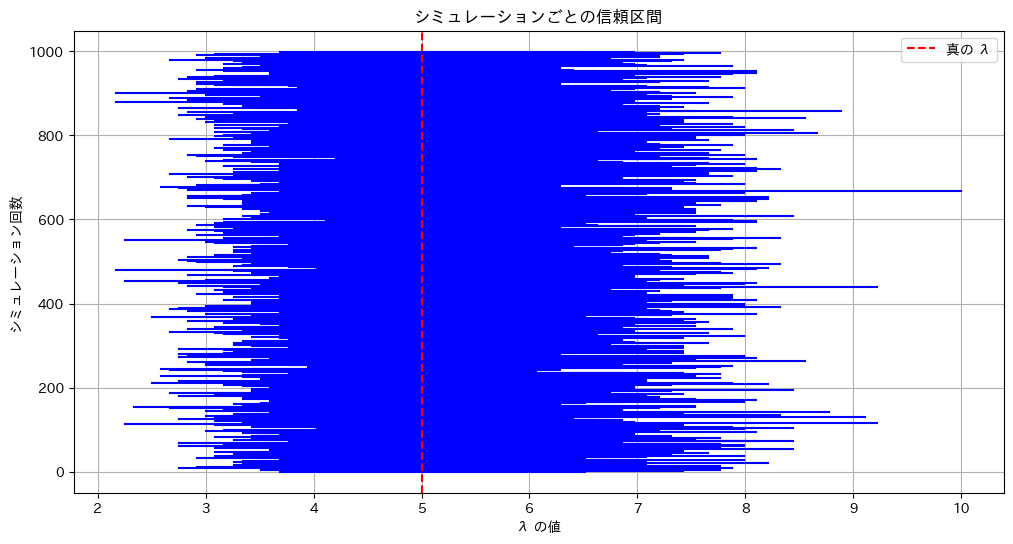
真のλが95.45%の確率で信頼区間内に含まれている様子が確認できました。
2021 Q3(2)[2-3]
ポアソン分布に従う確率変数の和Tからλの最尤推定量を求める問題をやりました。
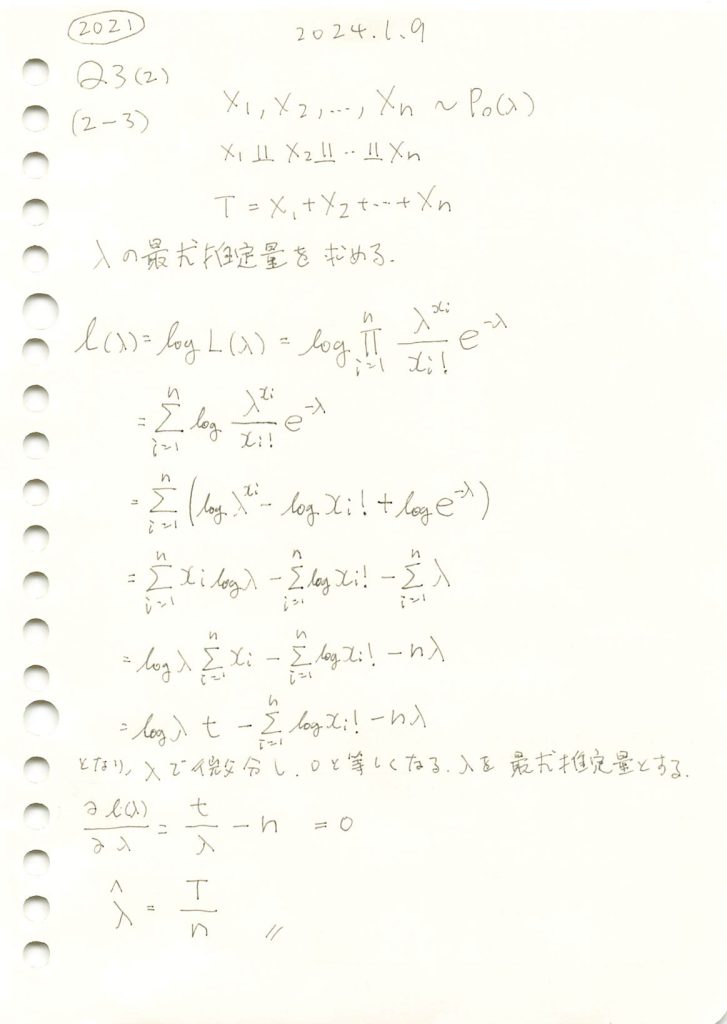
あとがき
![]() の式で計算すると簡単。
の式で計算すると簡単。
コード
scipyのminimizeで、最尤推定量を探索する。
# 2021 Q3(2)[2-3] 2024.8.28
import numpy as np
from scipy.optimize import minimize
from scipy.stats import poisson
# パラメータの設定
lambda_value = 5 # 真のパラメータ(実際のλ)
n = 10 # サンプル数
num_simulations = 1000 # シミュレーション回数
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_value, n)
# 尤度関数(負の対数尤度関数)
def negative_log_likelihood(lambda_hat, data):
# ポアソン分布に基づく対数尤度を計算。minimizeを用いるためマイナス符号をつける
return -np.sum(poisson.logpmf(data, lambda_hat))
# 最尤推定量の推定
initial_guess = np.mean(samples) # 初期値としてサンプルの平均を使用
result = minimize(negative_log_likelihood, x0=initial_guess, args=(samples,), bounds=[(0.001, None)])
lambda_mle = result.x[0]
# 結果を表示
print(f"実際のλ: {lambda_value}")
print(f"推定されたλの最尤推定値: {lambda_mle}")実際のλ: 5
推定されたλの最尤推定値: 4.9尤度関数のグラフを確認
# 2021 Q3(2)[2-3] 2024.8.28
import numpy as np
from scipy.stats import poisson
import matplotlib.pyplot as plt
# パラメータの設定
lambda_value = 5 # 真のパラメータ(実際のλ)
n = 10 # サンプル数
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_value, n)
# 尤度関数を定義
def likelihood(lambda_hat, data):
return np.prod(poisson.pmf(data, lambda_hat))
# 尤度関数と対数尤度関数の計算
lambda_range = np.linspace(0.1, 10, 500) # すべてのグラフで共通の範囲
likelihood_values = [likelihood(l, samples) for l in lambda_range]
log_likelihood_values = np.log(likelihood_values)
# 最大の尤度を与えるλを求める
max_likelihood_lambda = lambda_range[np.argmax(likelihood_values)]
# グラフのプロット
fig, ax = plt.subplots(2, 1, figsize=(10, 6))
# 尤度関数のプロット
ax[0].plot(lambda_range, likelihood_values, label='尤度', color='blue')
ax[0].axvline(x=max_likelihood_lambda, color='red', linestyle='--', label=f'最大尤度 λ = {max_likelihood_lambda:.2f}')
ax[0].set_title("尤度関数")
ax[0].set_xlabel("λ の値")
ax[0].set_ylabel("尤度")
ax[0].set_xlim(lambda_range[0], lambda_range[-1]) # 横軸を合わせる
ax[0].legend()
ax[0].grid(True)
# 対数尤度関数のプロット
ax[1].plot(lambda_range, log_likelihood_values, label='対数尤度', color='green')
ax[1].axvline(x=max_likelihood_lambda, color='red', linestyle='--', label=f'最大尤度 λ = {max_likelihood_lambda:.2f}')
ax[1].set_title("対数尤度関数")
ax[1].set_xlabel("λ の値")
ax[1].set_ylabel("対数尤度")
ax[1].set_xlim(lambda_range[0], lambda_range[-1]) # 横軸を合わせる
ax[1].legend()
ax[1].grid(True)
# グラフの表示
plt.tight_layout()
plt.show()
# 最終結果の表示
print(f"実際のλ: {lambda_value}")
print(f"推定されたλの最尤推定値: {max_likelihood_lambda}")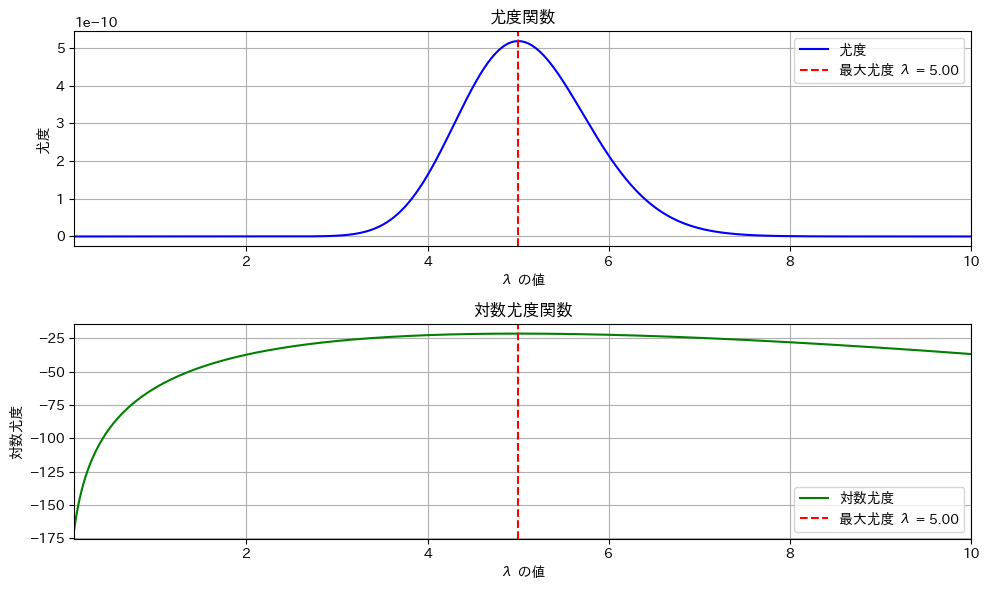
尤度関数でも対数尤度関数でも同じλでピークになる。
nが小さいとλの推定量の分散が大きくなるので誤差が大きくなる。上のグラフはたまたま5.00になった。n=100ぐらいにすると安定する。
シミュレーションによる計算
# 2021 Q3(2)[2-3] 2024.8.28
import numpy as np
# パラメータの設定
lambda_value = 5 # 真のパラメータ(実際のλ)
n = 10 # サンプル数
num_simulations = 1000 # シミュレーション回数
# ポアソン分布に従う n 個のサンプルを num_simulations 回生成
samples = np.random.poisson(lambda_value, (num_simulations, n))
# 各サンプルの和 T を計算
T = np.sum(samples, axis=1)
# λ の最尤推定量を計算
lambda_hat = T / n
# 結果を表示
print(f"実際のλ: {lambda_value}")
print(f"推定されたλの平均: {np.mean(lambda_hat)}")
print(f"推定されたλの分散: {np.var(lambda_hat)}")実際のλ: 5
推定されたλの平均: 5.0058
推定されたλの分散: 0.492926362021 Q3(2)[2-2]
ポアソン分布に従う独立な変数の和はパラメータλの十分統計量であることを学びました。
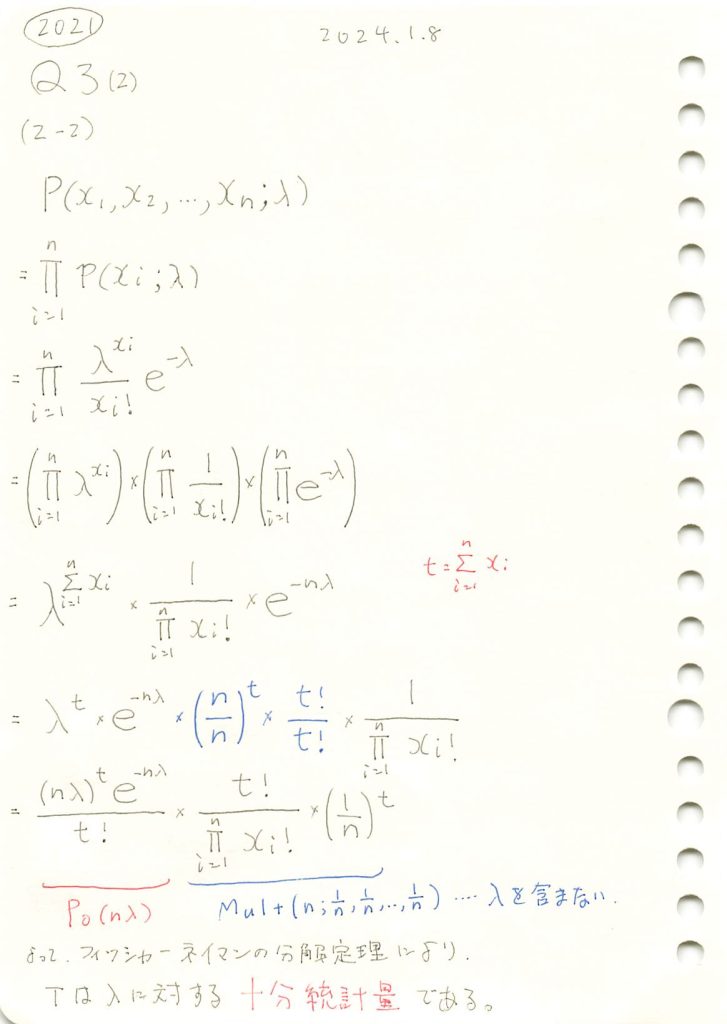
あとがき
![]() の式で示すと簡単。
の式で示すと簡単。
コード
ポアソン分布に従う10個の乱数の和 Tの分布を見てみます。
# 2024 Q3(2)[2-2] 2024.8.27
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
lambda_value = 5 # 真のパラメータ
n = 10 # サンプル数
num_simulations = 1000000 # シミュレーション回数
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_value, (num_simulations, n))
# 和 T を計算
T = np.sum(samples, axis=1)
# 和 T のヒストグラムをプロット
plt.hist(T, bins=30, density=True, alpha=0.75, color='blue')
plt.title(f'Tの分布 (n 個のポアソン変数の和)')
plt.xlabel('T')
plt.ylabel('確率密度')
plt.grid(True)
plt.show()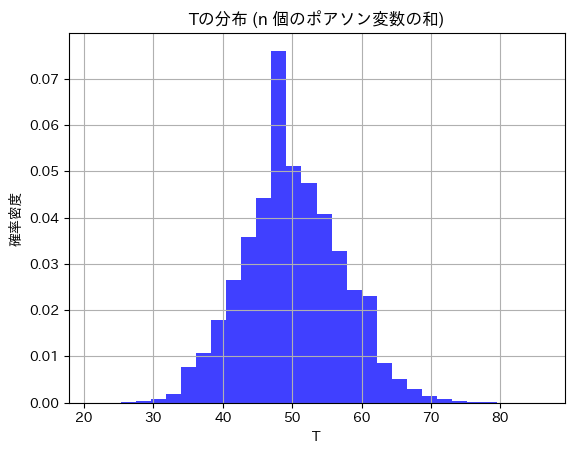
T~Po(nλ)になっています。
つぎにT=50の条件下での確率変数X1の分布を見てます。
# 2024 Q3(2)[2-2] 2024.8.27
import numpy as np
import matplotlib.pyplot as plt
# 条件付き分布の確認
# 例えば、T = 50 の場合におけるサンプルの分布を確認
T_value = 50 # T の特定の値
samples_given_T = samples[np.sum(samples, axis=1) == T_value]
# 確率変数の1つ (X1) の分布をプロット
plt.hist(samples_given_T[:, 0], bins=15, density=True, alpha=0.75, color='green')
plt.title(f'T={T_value} の条件付き X1 の分布')
plt.xlabel('X1')
plt.ylabel('確率密度')
plt.grid(True)
plt.show()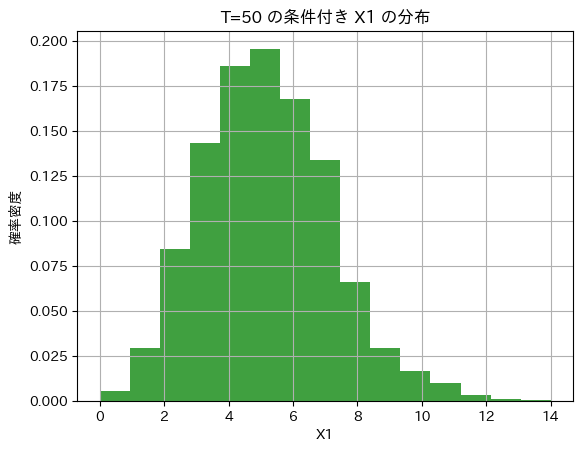
二項分布に従っているようです。
異なるλに対して、和T=50の条件下でのX1の分布を重ねて見てます。
# 2024 Q3(2)[2-2] 2024.8.27
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
# パラメータ設定
lambda_values = [3, 5, 7] # 異なる λ の値
n = 10 # サンプル数
num_simulations = 1000000 # シミュレーション回数
T_value = 50 # T の特定の値
plt.figure(figsize=(12, 6))
for lambda_value in lambda_values:
# ポアソン分布に従う n 個のサンプルを生成
samples = np.random.poisson(lambda_value, (num_simulations, n))
# T = T_value のサンプルを抽出
samples_given_T = samples[np.sum(samples, axis=1) == T_value]
# X1 の分布をプロット
counts, bin_edges, _ = plt.hist(samples_given_T[:, 0], bins=15, density=True, alpha=0.5, label=f'λ = {lambda_value}')
# 理論二項分布を描画
x1_min, x1_max = np.min(samples_given_T[:, 0]), np.max(samples_given_T[:, 0])
x = np.arange(x1_min, x1_max + 1)
estimated_p = 1 / n # 二項分布の p は 1/n で推定
binom_pmf = binom.pmf(x, T_value, estimated_p)
plt.plot(x, binom_pmf, 'k--', label=f'理論二項分布 Bin(T={T_value}, p=1/{n})')
plt.title(f'X1の分布 (T={T_value} 条件付き) と理論二項分布')
plt.xlabel('X1')
plt.ylabel('確率密度')
plt.legend()
plt.grid(True)
plt.show()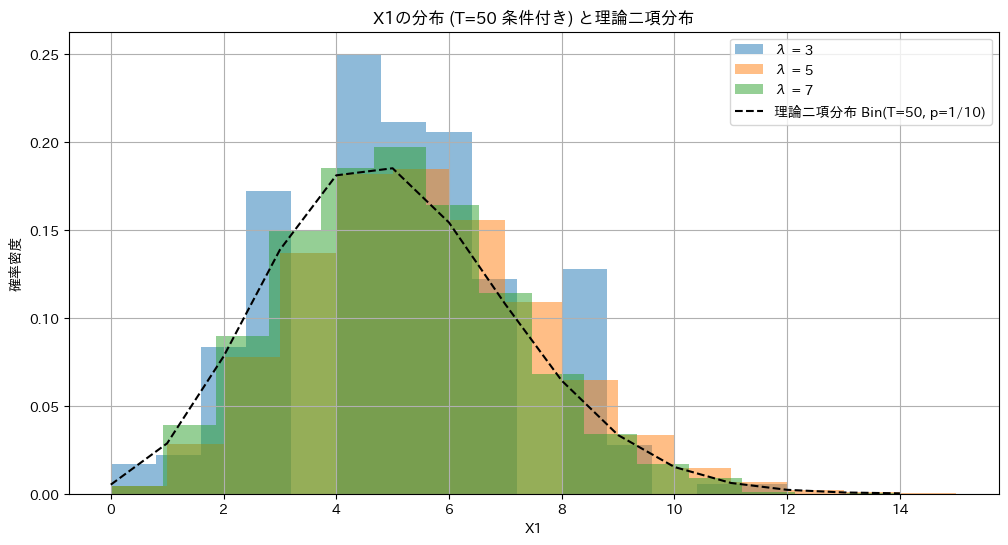
λに依存せず同じ二項分布に従います。よって統計量Tはλに対する十分統計量であることが示されました。
なお、X1~Xnの組は多項分布に従うが、簡単のためX1のみの分布を確認しました。X1は二項分布に従います。