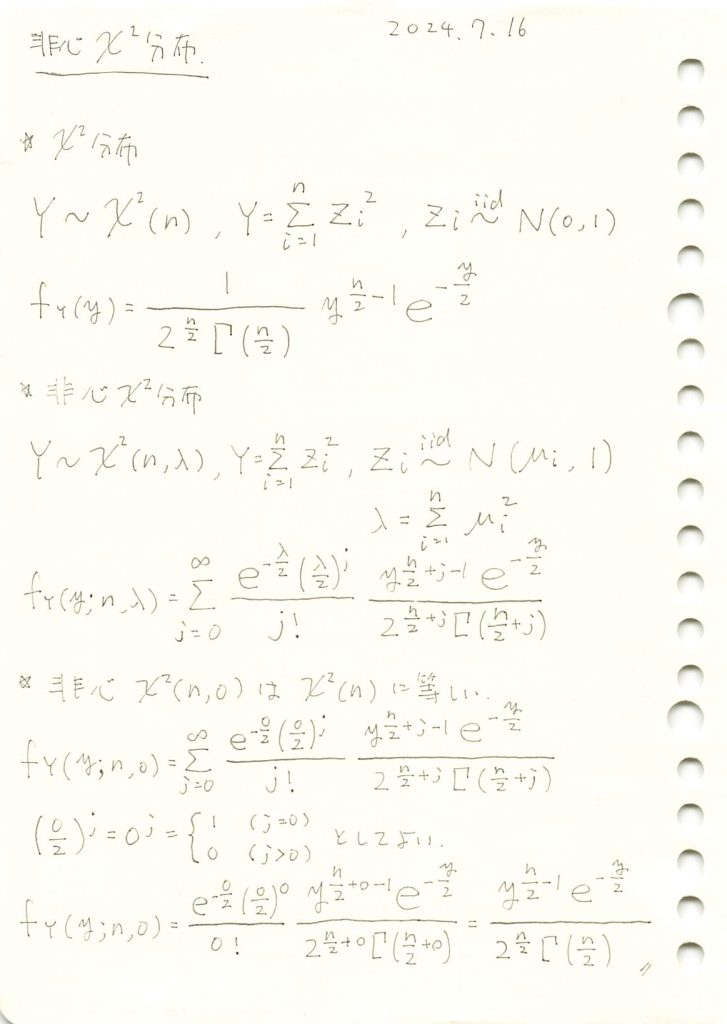2014 Q4(4)
5個の物体の重さを1つずつ2回量る場合で、誤差の分散を未知とし、全ての物体の重さが等しいとはいえないとする対立仮説のF検定量の非心度を求めました。
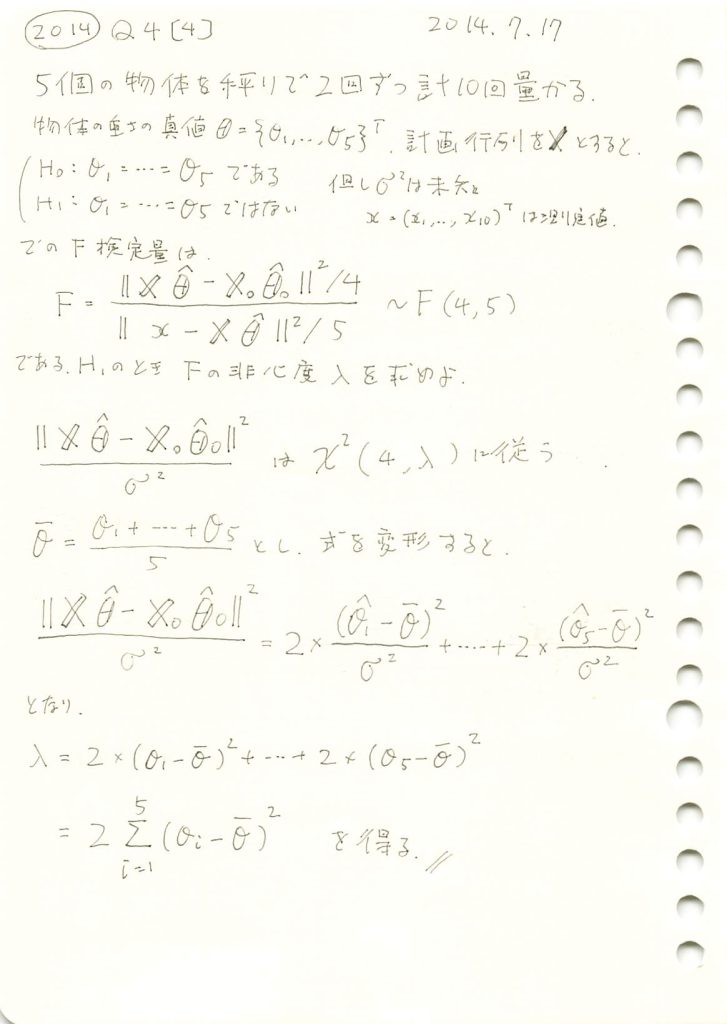
コード
真の値![]() から
から![]() へ徐々に変化させて、非心度λを計算し、その変化をグラフにプロットしてみます。
へ徐々に変化させて、非心度λを計算し、その変化をグラフにプロットしてみます。
# 2014 Q4(4) 2025.1.12
import numpy as np
import matplotlib.pyplot as plt
# 初期設定
theta_initial = np.array([10, 10, 10, 10, 10]) # 初期の真の値
theta_final = np.array([10, 20, 30, 40, 50]) # 最終的な真の値
steps = 50 # 変化のステップ数
# θを徐々に変化させる
theta_values = [theta_initial + (theta_final - theta_initial) * t / steps for t in range(steps + 1)]
# 非心度 λ を計算 (測定法(1): 係数は2)
lambdas_1 = [2 * np.sum((theta - np.mean(theta)) ** 2) for theta in theta_values]
# サンプルのインデックス(途中でいくつかの点を表示)
sample_indices = [0, 10, 20, 30, 40, 50]
# 真の値と対応する λ を取得 (測定法(1))
sample_theta_values = [theta_values[i] for i in sample_indices]
sample_lambdas_1 = [lambdas_1[i] for i in sample_indices]
# 視覚化
plt.figure(figsize=(10, 6))
plt.plot(range(steps + 1), lambdas_1, label="測定法(1): λ", color="blue")
plt.scatter(sample_indices, sample_lambdas_1, color="red", label="サンプル点")
for i, (theta, lam) in enumerate(zip(sample_theta_values, sample_lambdas_1)):
plt.text(sample_indices[i], lam, f"{np.round(theta, 1)}\nλ={lam:.1f}",
fontsize=10, ha="center", color="blue")
# グラフの設定
plt.xlabel("変化のステップ数")
plt.ylabel("非心度 λ")
plt.title("真の値の変化による非心度 λ の変化 (測定法(1))")
plt.legend()
plt.grid()
plt.show()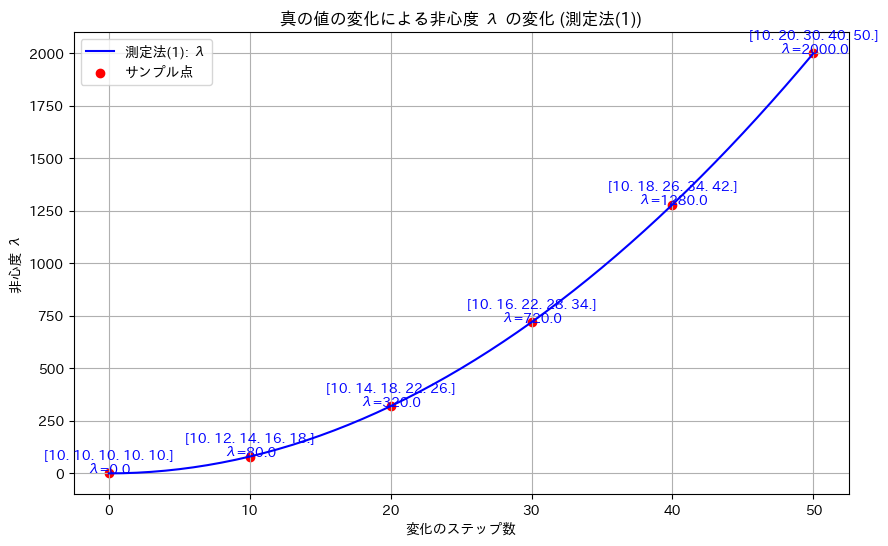
真の値![]() のばらつきが大きくなるにつれて、非心度λも非線形的に増加することが確認できました。
のばらつきが大きくなるにつれて、非心度λも非線形的に増加することが確認できました。
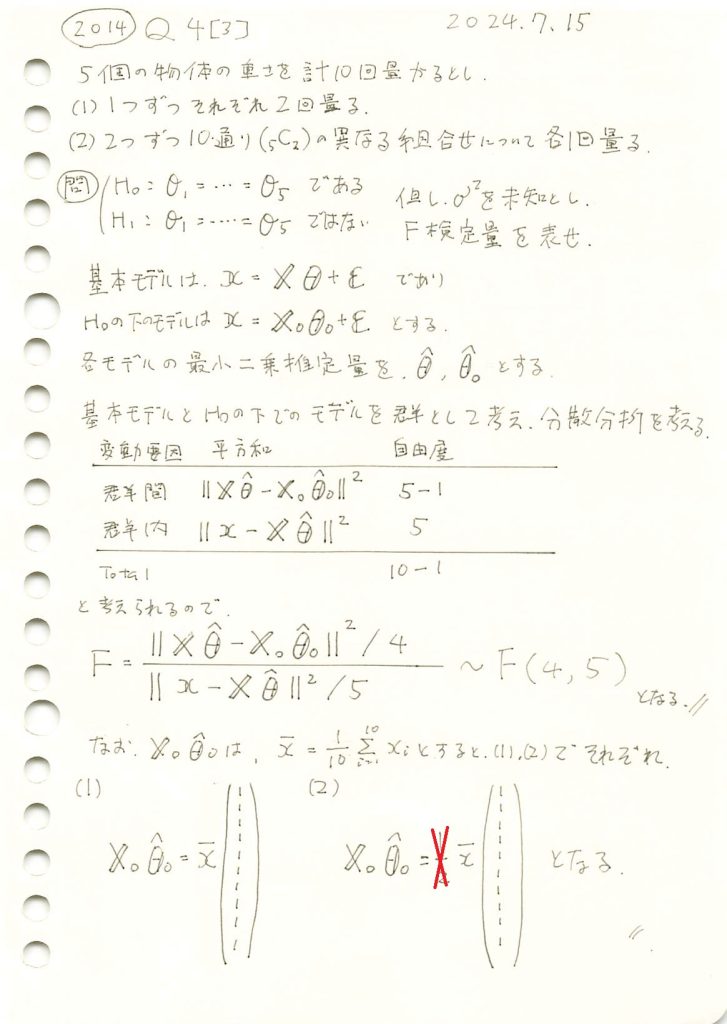
2014 Q4(3)
5個の物体の重さを、1つずつ2回量る場合と、2つずつ10通り量る場合で、誤差の分散を未知とし、全ての物体の重さが等しいとする帰無仮説を検定するF検定量を求めました。
コード
真の値![]() とし、二つの測定方法(1)と(2)においてシミュレーションを行い、F統計量を計算して、帰無仮説H0が棄却されるかを検定を行います。
とし、二つの測定方法(1)と(2)においてシミュレーションを行い、F統計量を計算して、帰無仮説H0が棄却されるかを検定を行います。
# 2014 Q4(3) 2025.1.11
import numpy as np
from scipy.stats import f
# パラメータ設定
n = 10 # 観測データ数
p_1 = 5 # 自由度(対立仮説モデルのパラメータ数)
p_0 = 1 # 自由度(帰無仮説モデルのパラメータ数)
nu_1 = p_1 - p_0 # 分子の自由度
nu_2 = n - p_1 # 分母の自由度
# 設計行列
X1 = np.array([ # 測定法 (1)
[1, 0, 0, 0, 0],
[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 1],
[0, 0, 0, 0, 1]
])
X2 = np.array([ # 測定法 (2)
[1, 1, 0, 0, 0],
[1, 0, 1, 0, 0],
[1, 0, 0, 1, 0],
[1, 0, 0, 0, 1],
[0, 1, 1, 0, 0],
[0, 1, 0, 1, 0],
[0, 1, 0, 0, 1],
[0, 0, 1, 1, 0],
[0, 0, 1, 0, 1],
[0, 0, 0, 1, 1]
])
X0 = np.ones((n, 1)) # 帰無仮説モデルの設計行列
# シミュレーション設定
true_theta = np.array([10, 10, 10, 10, 10]) # 真の値 (帰無仮説下)
sigma_squared = 1 # 誤差分散
n_simulations = 10000 # シミュレーション回数
# 統計量を保存するリスト
f_statistics_1 = []
f_statistics_2 = []
# シミュレーション
for _ in range(n_simulations):
# 観測データ生成
epsilon = np.random.normal(0, np.sqrt(sigma_squared), n)
x1 = X1 @ true_theta + epsilon
x2 = X2 @ true_theta + epsilon
# 最小二乗推定量
theta_hat_1 = np.linalg.inv(X1.T @ X1) @ X1.T @ x1
theta_hat_2 = np.linalg.inv(X2.T @ X2) @ X2.T @ x2
theta_hat_0_1 = np.linalg.inv(X0.T @ X0) @ X0.T @ x1
theta_hat_0_2 = np.linalg.inv(X0.T @ X0) @ X0.T @ x2
# 分子と分母の計算
numerator_1 = np.sum((X1 @ theta_hat_1 - X0 @ theta_hat_0_1) ** 2) / nu_1
denominator_1 = np.sum((x1 - X1 @ theta_hat_1) ** 2) / nu_2
f_stat_1 = numerator_1 / denominator_1
numerator_2 = np.sum((X2 @ theta_hat_2 - X0 @ theta_hat_0_2) ** 2) / nu_1
denominator_2 = np.sum((x2 - X2 @ theta_hat_2) ** 2) / nu_2
f_stat_2 = numerator_2 / denominator_2
f_statistics_1.append(f_stat_1)
f_statistics_2.append(f_stat_2)
# 平均 F 統計量を計算
f_stat_mean_1 = np.mean(f_statistics_1)
f_stat_mean_2 = np.mean(f_statistics_2)
# 理論 F 分布の平均計算
f_theoretical_mean = nu_2 / (nu_2 - 2) if nu_2 > 2 else None
# P値の計算
p_value_1 = 1 - f.cdf(f_stat_mean_1, nu_1, nu_2)
p_value_2 = 1 - f.cdf(f_stat_mean_2, nu_1, nu_2)
# 有意水準
alpha = 0.05
reject_null_1 = p_value_1 < alpha
reject_null_2 = p_value_2 < alpha
# 結果を出力
print("理論 F 分布の平均 (自由度 ν1 = {0}, ν2 = {1}): {2:.4f}".format(nu_1, nu_2, f_theoretical_mean))
print("\n測定法 (1):")
print(" 平均 F 統計量: {:.4f}".format(f_stat_mean_1))
print(" P値: {:.4e}".format(p_value_1))
print(" 帰無仮説を棄却するか: {}".format("はい" if reject_null_1 else "いいえ"))
print("\n測定法 (2):")
print(" 平均 F 統計量: {:.4f}".format(f_stat_mean_2))
print(" P値: {:.4e}".format(p_value_2))
print(" 帰無仮説を棄却するか: {}".format("はい" if reject_null_2 else "いいえ"))理論 F 分布の平均 (自由度 ν1 = 4, ν2 = 5): 1.6667
測定法 (1):
平均 F 統計量: 1.6255
P値: 3.0067e-01
帰無仮説を棄却するか: いいえ
測定法 (2):
平均 F 統計量: 1.6490
P値: 2.9569e-01
帰無仮説を棄却するか: いいえ二つの測定方法(1)と(2)においてシミュレーションを行い、F検定の結果、どちらの場合も帰無仮説H0が棄却されませんでした。
2014 Q4(2)
5個の物体の重さを、1つずつ2回量る場合と、2つずつ10通り量る場合で得た最小二乗法による各物体の重さの推定値の分散を求めました。

コード
シミュレーションにより、推定量![]() の分散を求め、理論分散と比較してみます。
の分散を求め、理論分散と比較してみます。
# 2014 Q4(2) 2025.1.10
import numpy as np
# シミュレーション設定
np.random.seed(42) # 再現性のための乱数シード
n_simulations = 10000 # シミュレーション回数
sigma_squared = 1 # 誤差分散
true_theta = np.array([10, 20, 30, 40, 50]) # 真の値 (任意設定)
# (1) 各物体を2回測定する場合
X1 = np.array([
[1, 0, 0, 0, 0],
[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 1],
[0, 0, 0, 0, 1]
])
# (2) 2つずつ異なる組み合わせで測定する場合
X2 = np.array([
[1, 1, 0, 0, 0],
[1, 0, 1, 0, 0],
[1, 0, 0, 1, 0],
[1, 0, 0, 0, 1],
[0, 1, 1, 0, 0],
[0, 1, 0, 1, 0],
[0, 1, 0, 0, 1],
[0, 0, 1, 1, 0],
[0, 0, 1, 0, 1],
[0, 0, 0, 1, 1]
])
# 理論分散
theoretical_variance_1 = sigma_squared / 2
theoretical_variance_2 = 7 * sigma_squared / 24
# シミュレーション結果を格納するリスト
variances_1 = []
variances_2 = []
for _ in range(n_simulations):
# 誤差を生成
epsilon = np.random.normal(0, np.sqrt(sigma_squared), 10)
# 測定値を生成
x1 = X1 @ true_theta + epsilon # (1) の場合
x2 = X2 @ true_theta + epsilon # (2) の場合
# 最小二乗推定量を計算
theta_hat_1 = np.linalg.inv(X1.T @ X1) @ X1.T @ x1
theta_hat_2 = np.linalg.inv(X2.T @ X2) @ X2.T @ x2
# 推定量の分散を計算
variances_1.append(np.mean((theta_hat_1 - true_theta)**2))
variances_2.append(np.mean((theta_hat_2 - true_theta)**2))
# シミュレーション結果の平均
simulated_variance_1 = np.mean(variances_1)
simulated_variance_2 = np.mean(variances_2)
# 結果の出力
print("(1) 理論分散:", theoretical_variance_1)
print("(1) シミュレーション分散:", simulated_variance_1)
print("(2) 理論分散:", theoretical_variance_2)
print("(2) シミュレーション分散:", simulated_variance_2)(1) 理論分散: 0.5
(1) シミュレーション分散: 0.5003499949049185
(2) 理論分散: 0.2916666666666667
(2) シミュレーション分散: 0.2926572303618685シミュレーションによる推定量![]() の分散は、理論分散とよく一致しました。
の分散は、理論分散とよく一致しました。
2014 Q4(1)-2
5個の物体の重さを、2つずつ10通り量る場合で、最小二乗法による各物体の重さの推定量を求めました。
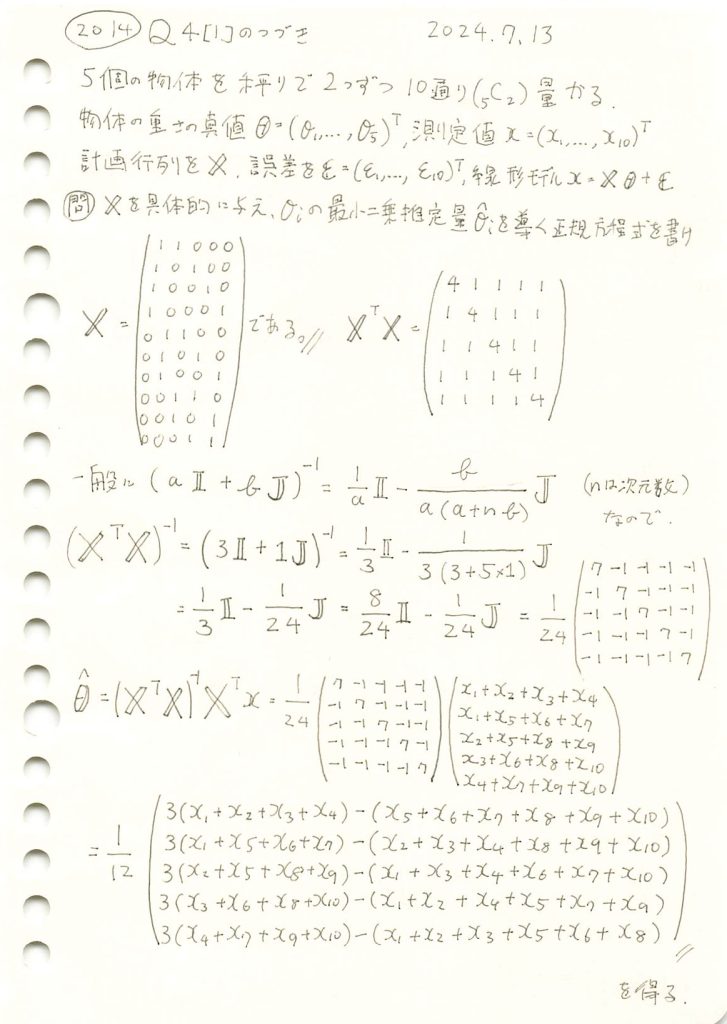
コード
最小二乗推定量![]() に基づいて計算してみます。
に基づいて計算してみます。
# 2014 Q4(1)-2 2025.1.9
import numpy as np
# 測定値
x = np.array([10.1, 12.3, 13.5, 14.6, 9.8, 11.7, 15.3, 12.8, 13.1, 14.2])
# 設計行列 X を構築 (2つずつ異なる組み合わせで10通り測定)
X = np.array([
[1, 1, 0, 0, 0],
[1, 0, 1, 0, 0],
[1, 0, 0, 1, 0],
[1, 0, 0, 0, 1],
[0, 1, 1, 0, 0],
[0, 1, 0, 1, 0],
[0, 1, 0, 0, 1],
[0, 0, 1, 1, 0],
[0, 0, 1, 0, 1],
[0, 0, 0, 1, 1]
])
# 最小二乗推定量の計算
X_transpose = X.T
theta_hat = np.linalg.inv(X_transpose @ X) @ X_transpose @ x
# 結果を出力
print("最小二乗推定量 (θ̂):", theta_hat)最小二乗推定量 (θ̂): [6.21666667 5.01666667 5.38333333 6.78333333 8.45 ]最小二乗推定量![]() が計算されました。
が計算されました。
次に、手計算で導いた式に基づいて計算してみます。
# 2014 Q4(1)-2 2025.1.9
import numpy as np
# 測定値
x = np.array([10.1, 12.3, 13.5, 14.6, 9.8, 11.7, 15.3, 12.8, 13.1, 14.2])
# θ^ を問題で導いた式に基づいて計算
theta_hat = np.array([
(3 * (x[0] + x[1] + x[2] + x[3]) - (x[4] + x[5] + x[6] + x[7] + x[8] + x[9])) / 12,
(3 * (x[0] + x[4] + x[5] + x[6]) - (x[1] + x[2] + x[3] + x[7] + x[8] + x[9])) / 12,
(3 * (x[1] + x[4] + x[7] + x[8]) - (x[0] + x[2] + x[3] + x[5] + x[6] + x[9])) / 12,
(3 * (x[2] + x[5] + x[7] + x[9]) - (x[0] + x[1] + x[3] + x[4] + x[6] + x[8])) / 12,
(3 * (x[3] + x[6] + x[8] + x[9]) - (x[0] + x[1] + x[2] + x[4] + x[5] + x[7])) / 12
])
# 結果を出力
print("最小二乗推定量 (θ̂):", theta_hat)
最小二乗推定量 (θ̂): [6.21666667 5.01666667 5.38333333 6.78333333 8.45 ]最小二乗推定量![]() が計算され、
が計算され、![]() で計算された値と一致しました。
で計算された値と一致しました。
2014 Q4(1)-1
5個の物体の重さを、1つずつ2回量る場合で、最小二乗法による各物体の重さの推定量を求めました。

コード
最小二乗推定量![]() に基づいて計算してみます。
に基づいて計算してみます。
# 2014 Q4(1)-1 2025.1.8
import numpy as np
# 測定値
x = np.array([5.1, 5.2, 7.3, 7.2, 6.8, 6.7, 4.9, 4.8, 5.5, 5.4])
# 設計行列 X を構築 (各物体を2回測定)
X = np.array([
[1, 0, 0, 0, 0],
[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 1],
[0, 0, 0, 0, 1]
])
# 最小二乗推定量の計算
X_transpose = X.T
theta_hat = np.linalg.inv(X_transpose @ X) @ X_transpose @ x
# 結果を出力
print("最小二乗推定量 (θ̂):", theta_hat)最小二乗推定量 (θ̂): [5.15 7.25 6.75 4.85 5.45]最小二乗推定量![]() が計算されました。
が計算されました。
次に、手計算で導いた式に基づいて計算してみます。
# 2014 Q4(1)-1 2025.1.8
import numpy as np
# 測定値
x = np.array([5.1, 5.2, 7.3, 7.2, 6.8, 6.7, 4.9, 4.8, 5.5, 5.4])
# θ^ を手計算の式に基づいて計算
theta_hat = np.array([
(x[0] + x[1]) / 2,
(x[2] + x[3]) / 2,
(x[4] + x[5]) / 2,
(x[6] + x[7]) / 2,
(x[8] + x[9]) / 2
])
# 結果を出力
print("最小二乗推定量 (θ̂):", theta_hat)最小二乗推定量 (θ̂): [5.15 7.25 6.75 4.85 5.45]最小二乗推定量![]() が計算され、
が計算され、![]() で計算された値と一致しました。
で計算された値と一致しました。
2014 Q3(2)
液体のサンプルの体積と重さから得た比重βがβ0であるという帰無仮説が棄却されないβの信頼区間を体積と重さの分散が未知の場合で求めました。

コード
分散未知の場合の信頼区間をシミュレーションし、カバー率が理論値(1 – α = 0.95)に一致するかを検証してみます。
# 2014 Q3(2) 2025.1.7
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t
# Parameters
n = 30 # サンプルサイズ
beta_true = 1.5 # 真のβ
sigma_X = 1.0 # Xの標準偏差
sigma_Y = 3.0 # Yの標準偏差
mu_X = 5.0 # Xの平均
alpha = 0.05 # 有意水準
num_simulations = 100 # シミュレーション回数
# 分散未知の場合の信頼区間を計算する関数
def confidence_interval_unknown_variance(X, Y, beta_0, alpha):
X_bar = np.mean(X)
Y_bar = np.mean(Y)
U = Y - beta_0 * X
S_square = np.sum((U - np.mean(U))**2) / (n - 1) # 標本分散
S_star = np.sqrt(S_square)
t_alpha = t.ppf(1 - alpha / 2, df=n - 1)
lower_bound = Y_bar / X_bar - t_alpha * S_star / (np.sqrt(n) * X_bar)
upper_bound = Y_bar / X_bar + t_alpha * S_star / (np.sqrt(n) * X_bar)
return lower_bound, upper_bound
# シミュレーション
intervals_unknown = []
contains_true_beta_unknown = []
for _ in range(num_simulations):
X = np.random.normal(mu_X, sigma_X, n)
epsilon = np.random.normal(0, np.sqrt(sigma_Y**2 + (beta_true * sigma_X)**2), n)
Y = beta_true * X + epsilon
# 信頼区間を計算
ci = confidence_interval_unknown_variance(X, Y, beta_true, alpha)
intervals_unknown.append(ci)
contains_true_beta_unknown.append(ci[0] <= beta_true <= ci[1])
# カバー率を計算
cover_rate_unknown = sum(contains_true_beta_unknown) / num_simulations
print("カバー率:")
print(f" 分散未知の場合: {cover_rate_unknown:.4f}")
# 可視化
plt.figure(figsize=(12, 8))
for i, ci in enumerate(intervals_unknown):
color = 'green' if contains_true_beta_unknown[i] else 'red'
plt.plot([ci[0], ci[1]], [i, i], color=color, marker='o', label="" if i > 0 else "信頼区間")
plt.axvline(x=beta_true, color='blue', linestyle='--', label=f"真のβ: {beta_true}")
plt.title("分散未知の場合の信頼区間 (各シミュレーション)", fontsize=16)
plt.xlabel("β", fontsize=12)
plt.ylabel("シミュレーション回数", fontsize=12)
plt.legend()
plt.grid()
plt.show()カバー率:
分散未知の場合: 0.9500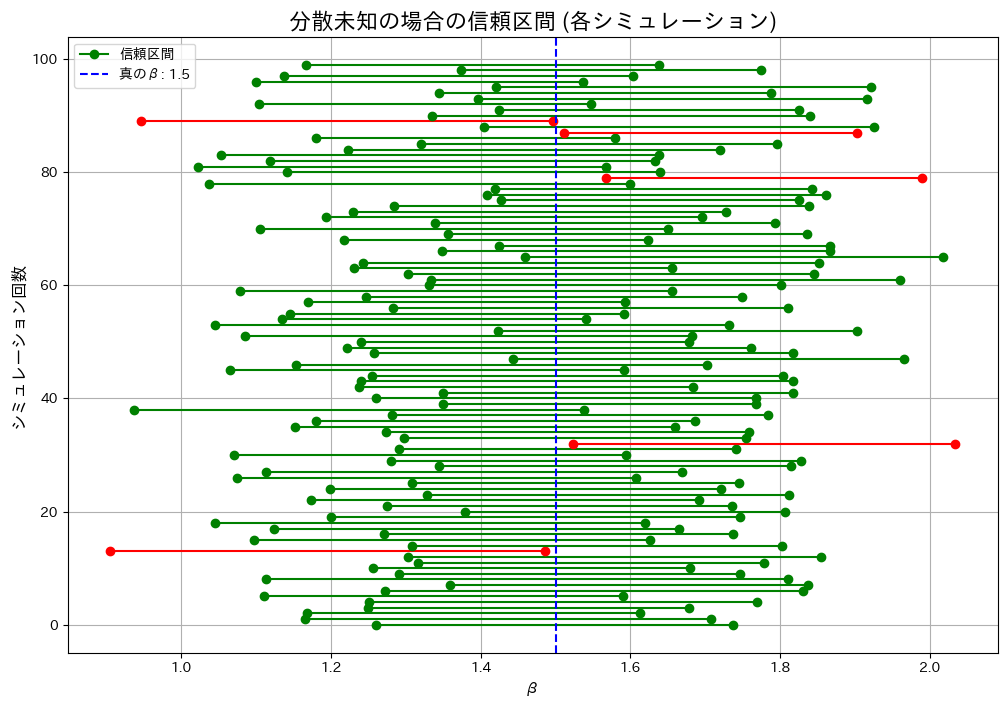
実行ごとに値は変動しましたが、カバー率は概ね理論値(1 – α = 0.95)に一致しました。
2014 Q3(2)
液体のサンプルの体積と重さから得た比重βがβ0であるという帰無仮説が棄却されないβの信頼区間を体積と重さの分散が既知の場合で求めました。

コード
分散既知の場合の信頼区間をシミュレーションし、カバー率が理論値(1 – α = 0.95)に一致するかを検証してみます。
# 2014 Q3(2) 2025.1.6
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Parameters
n = 30 # サンプルサイズ
beta_true = 1.5 # 真のβ
sigma_X = 1.0 # Xの標準偏差
sigma_Y = 3.0 # Yの標準偏差
mu_X = 5.0 # Xの平均
alpha = 0.05 # 有意水準
num_simulations = 100 # シミュレーション回数
# 分散既知の場合の信頼区間計算関数
def precise_confidence_interval(X, Y, sigma_X, sigma_Y, alpha):
X_bar = np.mean(X)
Y_bar = np.mean(Y)
z_alpha = norm.ppf(1 - alpha / 2)
numerator = n * X_bar * Y_bar
term1 = (n * X_bar * Y_bar)**2
term2 = (n * X_bar**2 - z_alpha**2 * sigma_X**2)
term3 = (n * Y_bar**2 - z_alpha**2 * sigma_Y**2)
denominator = n * X_bar**2 - z_alpha**2 * sigma_X**2
if term2 * term3 < 0:
raise ValueError("平方根の中身が負の値です:term2 * term3 は 0 以上でなければなりません。")
sqrt_term = np.sqrt(term1 - term2 * term3)
lower_bound = (numerator - sqrt_term) / denominator
upper_bound = (numerator + sqrt_term) / denominator
return lower_bound, upper_bound
# シミュレーション
intervals_precise = []
contains_true_beta_precise = []
for _ in range(num_simulations):
X = np.random.normal(mu_X, sigma_X, n)
epsilon = np.random.normal(0, np.sqrt(sigma_Y**2 + (beta_true * sigma_X)**2), n)
Y = beta_true * X + epsilon
# 信頼区間を計算
ci = precise_confidence_interval(X, Y, sigma_X, sigma_Y, alpha)
intervals_precise.append(ci)
contains_true_beta_precise.append(ci[0] <= beta_true <= ci[1])
# カバー率を計算
cover_rate_precise = sum(contains_true_beta_precise) / num_simulations
print("カバー率:")
print(f" 分散既知の場合: {cover_rate_precise:.4f}")
# 可視化
plt.figure(figsize=(12, 8))
for i, ci in enumerate(intervals_precise):
color = 'green' if contains_true_beta_precise[i] else 'red'
plt.plot([ci[0], ci[1]], [i, i], color=color, marker='o', label="" if i > 0 else "信頼区間")
plt.axvline(x=beta_true, color='blue', linestyle='--', label=f"真のβ: {beta_true}")
plt.title("分散既知の場合の信頼区間 (各シミュレーション)", fontsize=16)
plt.xlabel("β", fontsize=12)
plt.ylabel("シミュレーション回数", fontsize=12)
plt.legend()
plt.grid()
plt.show()カバー率:
分散既知の場合: 0.9500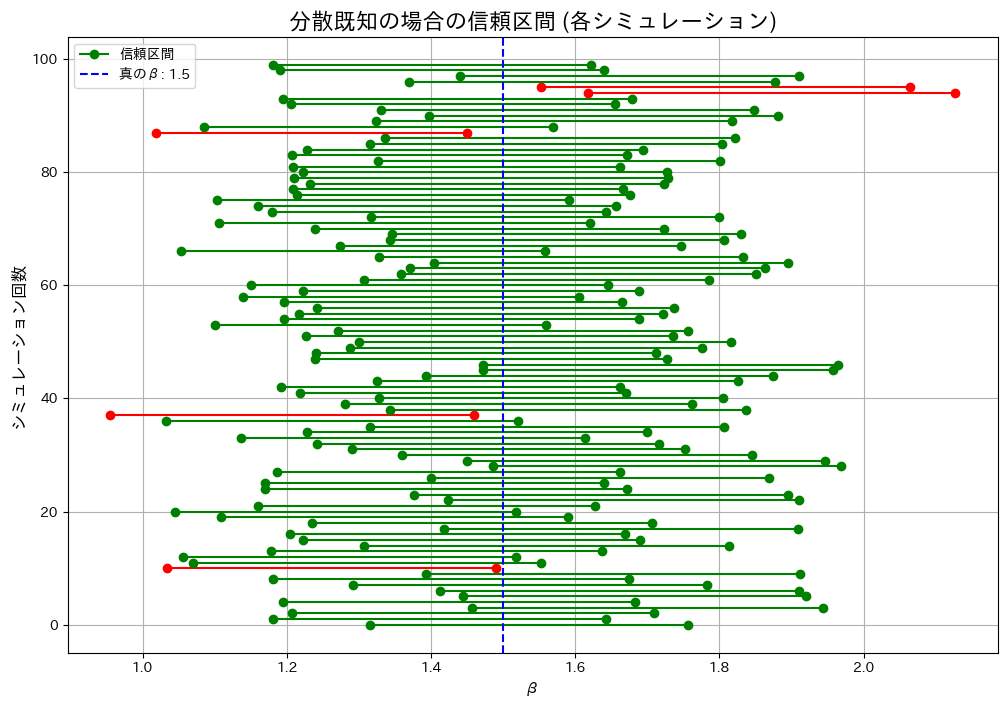
実行ごとに値は変動しましたが、カバー率は概ね理論値(1 – α = 0.95)に一致しました。
2014 Q3(1)
液体のサンプルの体積と重さから比重がβ0であるという検定を体積と重さの分散が既知の場合と未知の場合でそれぞれ方式を求めました。

コード
帰無仮説![]() の下で、真の値
の下で、真の値![]() が仮説と一致する場合(
が仮説と一致する場合(![]() )と異なる場合(
)と異なる場合(![]() )におけるZ検定とT検定の棄却率を比較します。
)におけるZ検定とT検定の棄却率を比較します。
# 2014 Q3(1) 2025.1.5 (2025.1.6修正)
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, t
# Parameters
n = 30 # サンプルサイズ
beta_0 = 1.2 # 仮説のβ
sigma_X = 1.0 # Xの標準偏差
sigma_Y = 3.0 # Yの標準偏差
mu_X = 5.0 # Xの平均 (十分大きく設定)
alpha = 0.05 # 有意水準
num_simulations = 1000 # シミュレーション回数
# 分散の妥当性を確認
beta_true_values = [1.2, 1.5] # 真のβの候補
# 結果を格納するリスト
simulated_Z_dict = {}
simulated_T_dict = {}
rejection_rates_Z = {}
rejection_rates_T = {}
for beta_true in beta_true_values:
if sigma_Y**2 <= (beta_true * sigma_X)**2:
raise ValueError(f"sigma_Y^2は(beta_true * sigma_X)^2より大きくなければなりません (beta_true={beta_true})。")
# 誤差項の分散を計算
sigma_epsilon_squared = sigma_Y**2 + (beta_true * sigma_X)**2
# Z統計量とT統計量を格納するリスト
simulated_Z = []
simulated_T = []
reject_count_Z = 0
reject_count_T = 0
for _ in range(num_simulations):
# Xを正規分布で生成
X = np.random.normal(mu_X, sigma_X, n) # 平均mu_X、標準偏差sigma_X
epsilon = np.random.normal(0, np.sqrt(sigma_epsilon_squared), n) # 誤差項
# Yを生成
Y = beta_true * X + epsilon
# Z検定 (分散既知)
X_bar = np.mean(X)
Y_bar = np.mean(Y)
Z = (Y_bar - beta_0 * X_bar) / np.sqrt((sigma_Y**2 + beta_0**2 * sigma_X**2) / n)
simulated_Z.append(Z)
if abs(Z) > norm.ppf(1 - alpha / 2): # 両側検定
reject_count_Z += 1
# T検定 (分散未知)
U = Y - beta_0 * X
U_bar = np.mean(U)
S_square = np.sum((U - U_bar)**2) / (n - 1)
T = (Y_bar - beta_0 * X_bar) / np.sqrt(S_square / n)
simulated_T.append(T)
if abs(T) > t.ppf(1 - alpha / 2, df=n - 1): # 両側検定
reject_count_T += 1
simulated_Z_dict[beta_true] = simulated_Z
simulated_T_dict[beta_true] = simulated_T
rejection_rates_Z[beta_true] = reject_count_Z / num_simulations
rejection_rates_T[beta_true] = reject_count_T / num_simulations
# 棄却率を表示
print("検定条件: H0: β = 1.2")
for beta_true in beta_true_values:
print(f"真のβ = {beta_true}: Z検定の棄却率 = {rejection_rates_Z[beta_true]:.4f}, T検定の棄却率 = {rejection_rates_T[beta_true]:.4f}")
# グラフ用の範囲を定義
x_values = np.linspace(-4, 4, 1000)
# 理論的なZ分布 (帰無仮説H0: beta = beta_0)
z_pdf = norm.pdf(x_values, 0, 1)
# Z分布のプロット
plt.figure(figsize=(12, 6))
plt.plot(x_values, z_pdf, label="理論分布 (H0: 標準正規分布)", color='blue')
for beta_true, simulated_Z in simulated_Z_dict.items():
plt.hist(simulated_Z, bins=30, density=True, alpha=0.6, label=f"シミュレーション (真のβ = {beta_true})")
plt.axvline(x=norm.ppf(1 - alpha / 2), color='red', linestyle='dashed', label=f"有意水準の境界 (+{norm.ppf(1 - alpha / 2):.2f})")
plt.axvline(x=-norm.ppf(1 - alpha / 2), color='red', linestyle='dashed', label=f"有意水準の境界 (-{norm.ppf(1 - alpha / 2):.2f})")
plt.title("Z分布: 理論分布とシミュレーションの比較 (真のβの変化)", fontsize=16)
plt.xlabel("Z値", fontsize=12)
plt.ylabel("密度", fontsize=12)
plt.legend()
plt.grid()
plt.show()
# 理論的なT分布 (帰無仮説H0: beta = beta_0)
t_pdf = t.pdf(x_values, df=n - 1)
# T分布のプロット
plt.figure(figsize=(12, 6))
plt.plot(x_values, t_pdf, label=f"理論分布 (H0: t分布, 自由度={n - 1})", color='blue')
for beta_true, simulated_T in simulated_T_dict.items():
plt.hist(simulated_T, bins=30, density=True, alpha=0.6, label=f"シミュレーション (真のβ = {beta_true})")
plt.axvline(x=t.ppf(1 - alpha / 2, df=n - 1), color='red', linestyle='dashed', label=f"有意水準の境界 (+{t.ppf(1 - alpha / 2, df=n - 1):.2f})")
plt.axvline(x=-t.ppf(1 - alpha / 2, df=n - 1), color='red', linestyle='dashed', label=f"有意水準の境界 (-{t.ppf(1 - alpha / 2, df=n - 1):.2f})")
plt.title("T分布: 理論分布とシミュレーションの比較 (真のβの変化)", fontsize=16)
plt.xlabel("T値", fontsize=12)
plt.ylabel("密度", fontsize=12)
plt.legend()
plt.grid()
plt.show()検定条件: H0: β = 1.2
真のβ = 1.2: Z検定の棄却率 = 0.0390, T検定の棄却率 = 0.0400
真のβ = 1.5: Z検定の棄却率 = 0.7080, T検定の棄却率 = 0.6490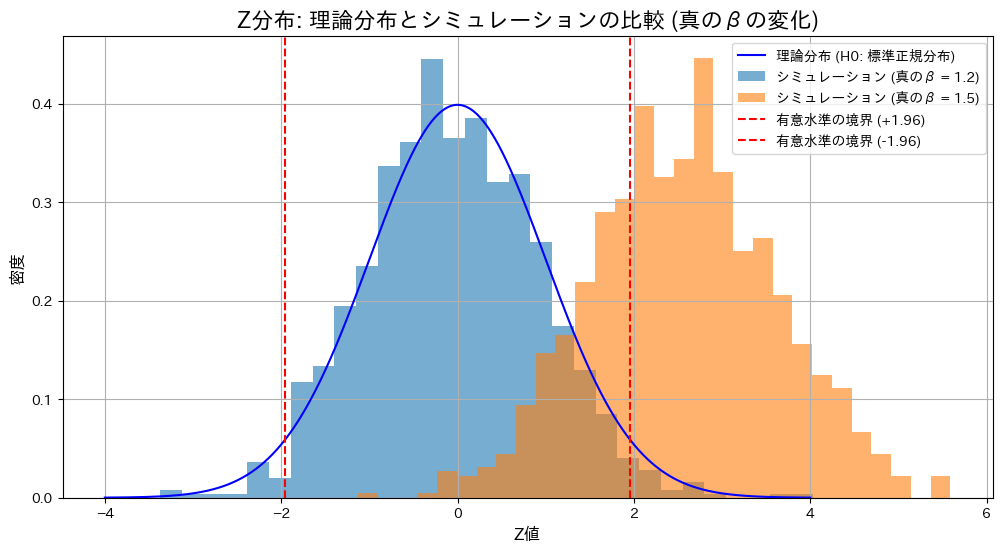
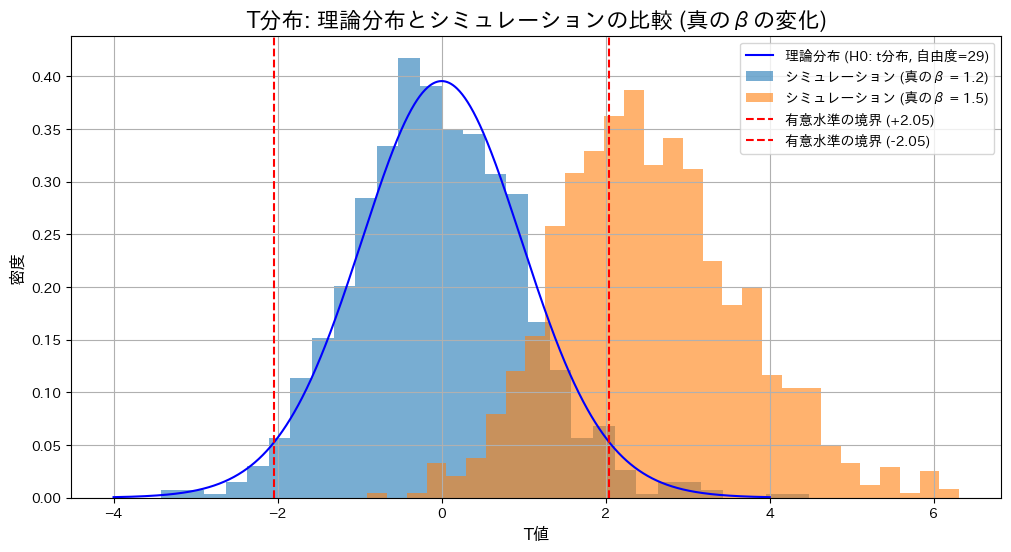
帰無仮説が正しい場合(![]() )、Z検定とT検定の棄却率は有意水準付近で期待通りの結果を示しました。一方、真の値が異なる場合(
)、Z検定とT検定の棄却率は有意水準付近で期待通りの結果を示しました。一方、真の値が異なる場合(![]() )、両検定で棄却域が大幅に上昇し、帰無仮説を適切に棄却できていることが確認されました。また、真の値が異なる場合には、Z検定の棄却率がT検定をわずかに上回る結果となりました。これは、分散既知の場合のZ検定が分散未知のT検定に比べて統計量の推定が安定しているためと考えられます。
)、両検定で棄却域が大幅に上昇し、帰無仮説を適切に棄却できていることが確認されました。また、真の値が異なる場合には、Z検定の棄却率がT検定をわずかに上回る結果となりました。これは、分散既知の場合のZ検定が分散未知のT検定に比べて統計量の推定が安定しているためと考えられます。
2014 Q2(5)
n個の一様分布の順序統計量の期待値を求めました。
コード
サンプルサイズn=5として、一様分布の順序統計量![]() をシミュレーションし、その確率密度の形状を確認するとともに、期待値がどのようになるか確かめます。
をシミュレーションし、その確率密度の形状を確認するとともに、期待値がどのようになるか確かめます。
# 2014 Q2(5) 2024.1.4
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションの設定
n_simulations = 10**6 # サンプルサイズ
n = 5 # サンプルサイズ (n個の確率変数)
# 一様分布からサンプリング
U = np.random.uniform(0, 1, (n_simulations, n))
# PDF (確率密度関数) および期待値をプロット
j_values = range(1, n + 1) # j を 1 から n まで変化させる
plt.figure(figsize=(14, 8))
colors = ['blue', 'orange', 'green', 'red', 'purple'] # 色の設定
for idx, j in enumerate(j_values):
# j 番目の順序統計量を取得
U_j = np.sort(U, axis=1)[:, j-1]
# 理論値のPDFを計算
u = np.linspace(0, 1, 1000)
pdf_theory = (n * np.math.comb(n-1, j-1)) * (u**(j-1)) * ((1-u)**(n-j))
# ヒストグラム (シミュレーション結果)
plt.hist(U_j, bins=50, density=True, alpha=0.5, label=f'j = {j} (シミュレーション)', color=colors[idx])
# 理論値のPDFをプロット
plt.plot(u, pdf_theory, linestyle='--', color=colors[idx], label=f'j = {j} (理論)')
# 理論値の期待値を直線で追加
expected_value = j / (n + 1)
plt.axvline(x=expected_value, color=colors[idx], linestyle=':', label=f'j = {j} 期待値 = {expected_value:.2f}')
# グラフ装飾
plt.title('順序統計量 U_(j) の PDF と期待値 (理論 vs シミュレーション)', fontsize=16)
plt.xlabel('値', fontsize=12)
plt.ylabel('密度', fontsize=12)
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()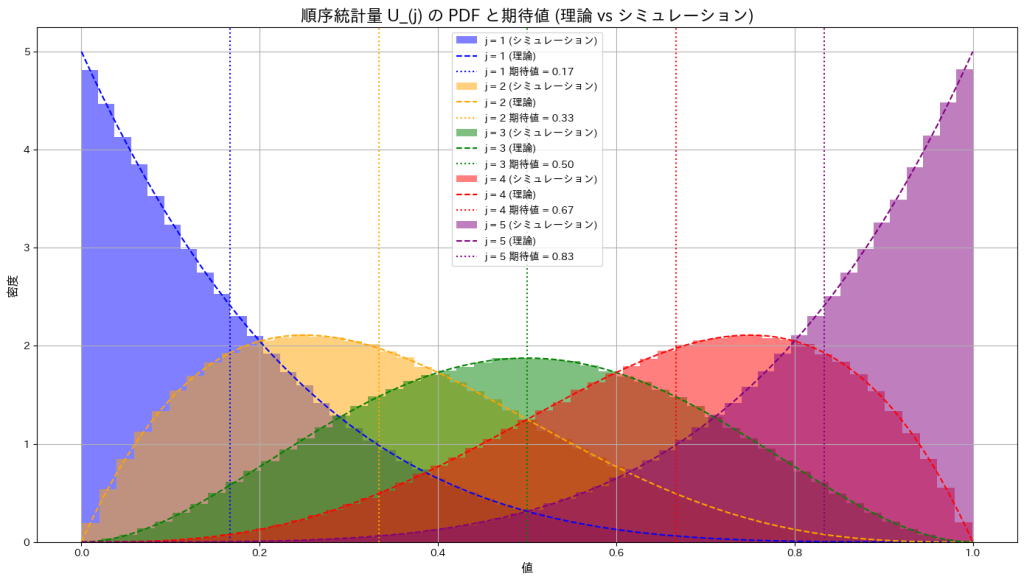
一様分布の順序統計量![]() の確率密度は、jが小さいときには左に寄り、jが大きくなると右に寄る形状を示します。また期待値はj/(n+1)であるため0~1の範囲をn+1で均等に分割した値に一致することが確認できました。
の確率密度は、jが小さいときには左に寄り、jが大きくなると右に寄る形状を示します。また期待値はj/(n+1)であるため0~1の範囲をn+1で均等に分割した値に一致することが確認できました。