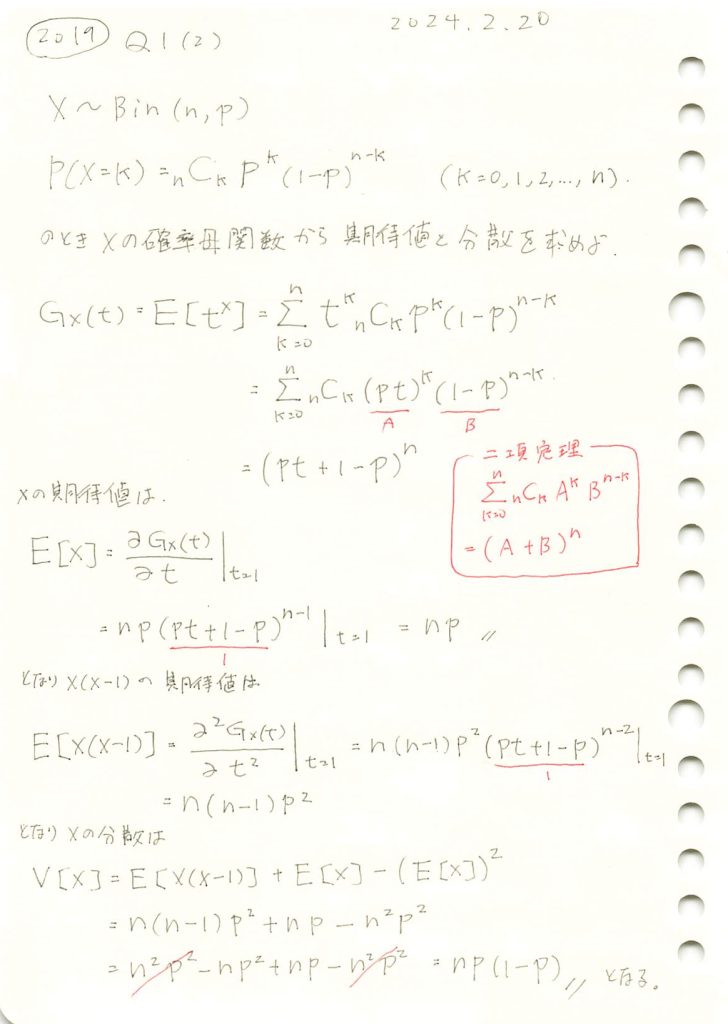2019 Q2(4)
損失関数の期待値を導出しそれが最小となるパラメータαを求める問題をやりました。
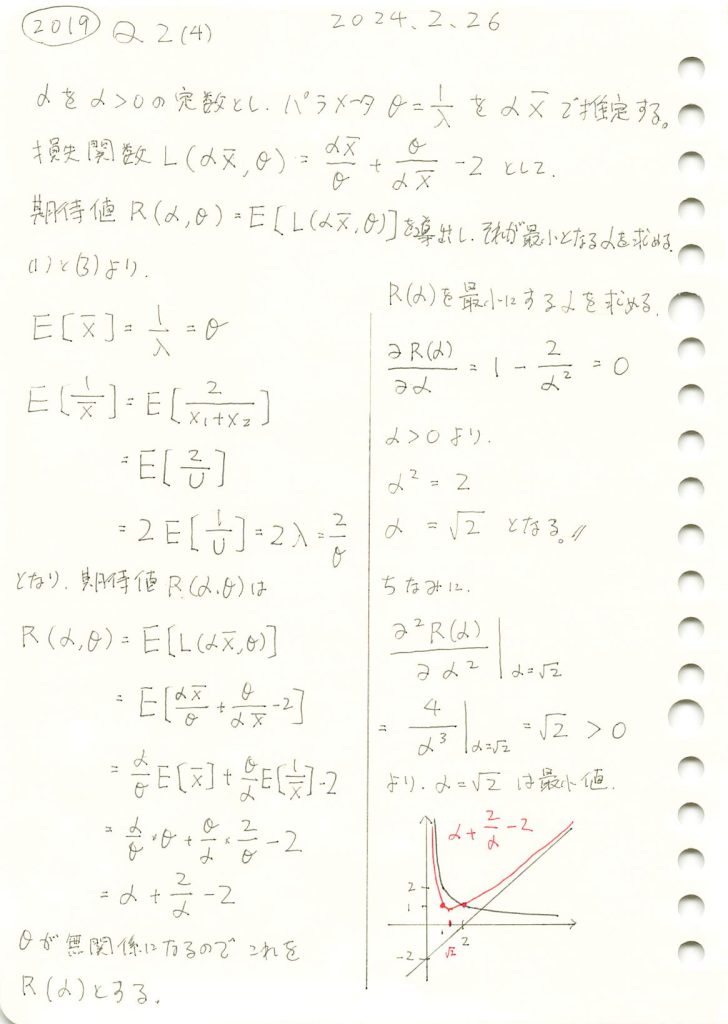
コード
数値シミュレーションによりR(α)が最小値になるαを見つけます。
# 2019 Q2(4) 2024.9.16
import numpy as np
import matplotlib.pyplot as plt
# 損失関数 R(α) の定義
def R(alpha):
return alpha + 2 / alpha - 2
# α の範囲を設定 (0.1 から 3 まで、細かいステップで計算)
alpha_range = np.linspace(0.1, 3, 1000)
# 損失関数 R(α) の計算
R_values = R(alpha_range)
# 最小値を取る α の確認 (numpy の argmin を使って最小値を見つける)
min_index = np.argmin(R_values)
min_alpha = alpha_range[min_index]
min_R = R_values[min_index]
# グラフのプロット
plt.figure(figsize=(8, 6))
plt.plot(alpha_range, R_values, label='R(α)')
plt.axvline(np.sqrt(2), color='red', linestyle='--', label=r'$\alpha = \sqrt{2}$')
plt.scatter(min_alpha, min_R, color='red', zorder=5, label=f'最小値: α={min_alpha:.2f}, R(α)={min_R:.2f}')
plt.xlabel(r'$\alpha$')
plt.ylabel(r'$R(\alpha)$')
plt.title(r'$R(\alpha)$ の最小値確認 (数値シミュレーション)')
plt.legend()
plt.grid(True)
plt.show()
# 最小値の表示
print(f'数値シミュレーションでの最小値 α: {min_alpha}, R(α): {min_R}')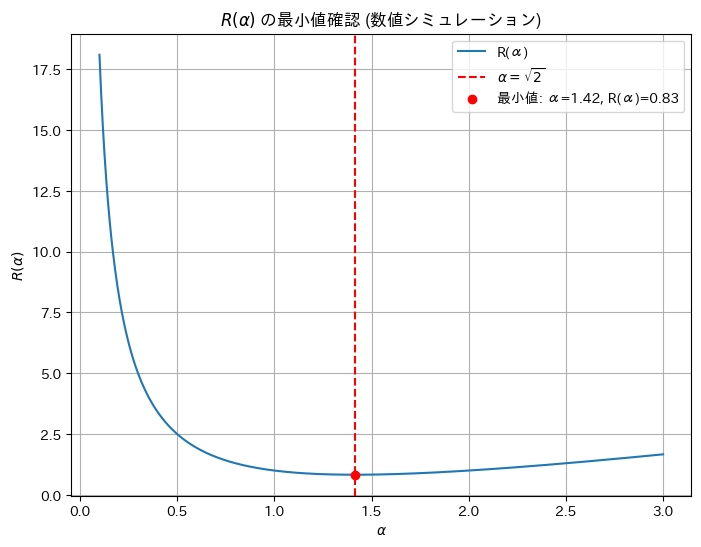
数値シミュレーションでの最小値 α: 1.4150150150150151, R(α): 0.8284275786822475手計算と近い値になりました。
極値付近が少し平らなので、αの範囲を1.0~2.0に変更し拡大してみます。
import numpy as np
import matplotlib.pyplot as plt
# 損失関数 R(α) の定義
def R(alpha):
return alpha + 2 / alpha - 2
# α の範囲を 1 から 2 に設定
alpha_range = np.linspace(1, 2, 1000)
# 損失関数 R(α) の計算
R_values = R(alpha_range)
# 最小値を取る α の確認 (numpy の argmin を使って最小値を見つける)
min_index = np.argmin(R_values)
min_alpha = alpha_range[min_index]
min_R = R_values[min_index]
# グラフのプロット
plt.figure(figsize=(8, 6))
plt.plot(alpha_range, R_values, label='R(α)')
plt.axvline(np.sqrt(2), color='red', linestyle='--', label=r'$\alpha = \sqrt{2}$')
plt.scatter(min_alpha, min_R, color='red', zorder=5, label=f'最小値: α={min_alpha:.4f}, R(α)={min_R:.4f}')
plt.xlabel(r'$\alpha$')
plt.ylabel(r'$R(\alpha)$')
plt.title(r'$R(\alpha)$ の最小値確認 (αの範囲: 1 から 2)')
plt.legend()
plt.grid(True)
plt.show()
# 最小値の表示
print(f'数値シミュレーションでの最小値 α: {min_alpha}, R(α): {min_R}')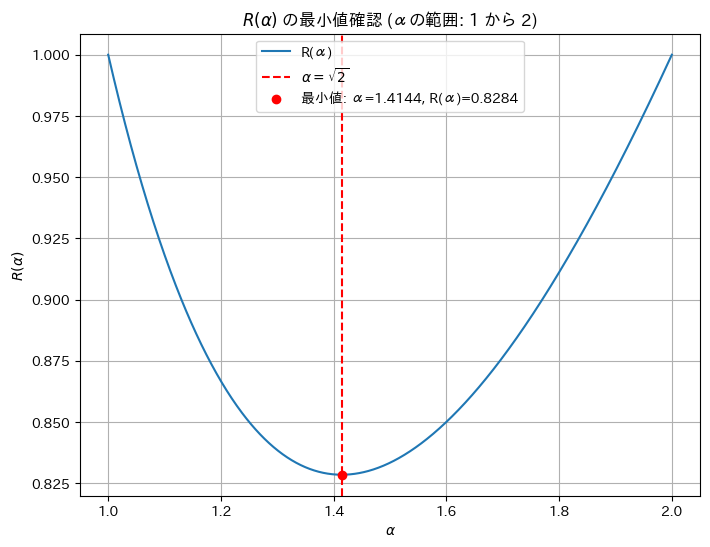
数値シミュレーションでの最小値 α: 1.4144144144144144, R(α): 0.8284271532679175最小値が取れていることが分かりました。
2019 Q2(3)
(2)で求めた確率密度関数において確率変数Uの逆数の期待値を求めました。
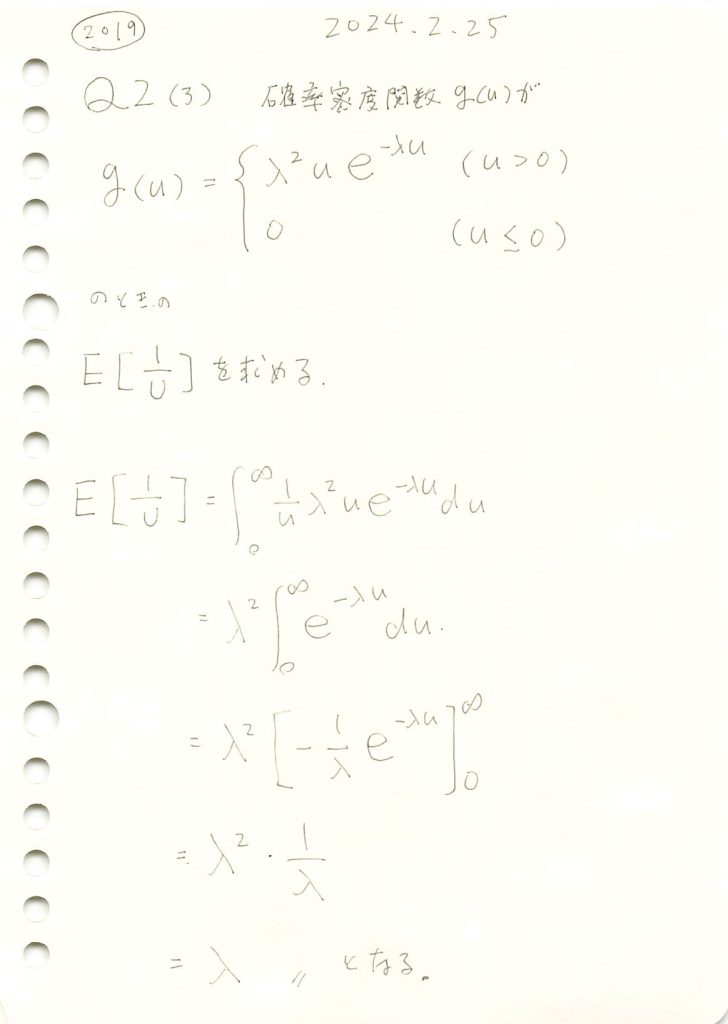
コード
数式を使って1/Uの期待値を求めます。
# 2019 Q2(3) 2024.9.15
import sympy as sp
# 変数の定義
u, lambda_value = sp.symbols('u lambda', positive=True, real=True)
# ガンマ分布の確率密度関数 g(u) = λ^2 * u * exp(-λ * u)
g_u = lambda_value**2 * u * sp.exp(-lambda_value * u)
# 1/U の期待値の積分
integrand = (1/u) * g_u # 1/u * g(u)
# 積分の実行
expectation = sp.integrate(integrand, (u, 0, sp.oo))
# 結果の簡略化
expectation_simplified = sp.simplify(expectation)
# 結果の表示
display(expectation_simplified)手計算と一致します。
次に、数値シミュレーションを行います。
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
lambda_value = 2 # λ=2
num_samples = 100000 # サンプルの数
# 指数分布に従う乱数 X1, X2 を生成
X1 = np.random.exponential(scale=1/lambda_value, size=num_samples)
X2 = np.random.exponential(scale=1/lambda_value, size=num_samples)
# U = X1 + X2 の計算
U = X1 + X2
# 1/U の計算
inv_U = 1 / U
# シミュレーションの結果からの平均値
simulation_result = np.mean(inv_U)
# 理論値 E[1/U] = λ
theoretical_value = lambda_value
# 結果の表示
print(f'シミュレーションによる E[1/U]: {simulation_result}')
print(f'理論値 E[1/U]: {theoretical_value}')
# ヒストグラムの描画
plt.hist(inv_U, bins=50, density=True, alpha=0.7, label='シミュレーション結果')
plt.axvline(theoretical_value, color='r', linestyle='--', label=f'理論値 E[1/U] = {theoretical_value}')
plt.xlabel('1/U')
plt.ylabel('確率密度')
plt.title('シミュレーションによる 1/U の分布と理論値の比較')
plt.legend()
plt.show()シミュレーションによる E[1/U]: 1.9928303711222939
理論値 E[1/U]: 2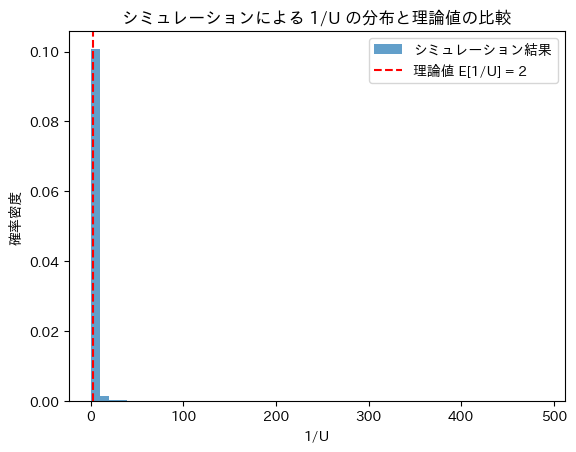
シミュレーションによりE[1/U]は理論値に近づきました。分散は発散するためヒストグラムにすると大きなバラつきが見られます。
2019 Q2(2)
独立な指数分布に従う2変数の和の確率密度関数を求めました。

コード
数式を使ってUの確率密度関数を求めます。
# 2019 Q2(2) 2024.9.14
import sympy as sp
# 変数の定義
x, u, lambda_value = sp.symbols('x u lambda', positive=True, real=True)
# 指数分布の確率密度関数 (PDF) f(x)
f_x = lambda_value * sp.exp(-lambda_value * x)
# 畳み込み積分を計算して、g(u) = f(x) * f(u - x) の形式にする
g_u = sp.integrate(f_x * lambda_value * sp.exp(-lambda_value * (u - x)), (x, 0, u))
# 簡略化
g_u_simplified = sp.simplify(g_u)
# 結果の表示
display(g_u_simplified)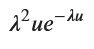
X1 (X2)と、Uの確率密度関数を重ねて描画してみます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # λ=2
x_range = np.linspace(0, 5, 1000) # X1, X2 の範囲
# X1, X2 の指数分布の確率密度関数 (PDF) - 同じなので1つにまとめる
pdf_X1_X2 = lambda_value * np.exp(-lambda_value * x_range)
# U = X1 + X2 は形状パラメータk=2、スケールパラメータθ=1/λのガンマ分布
u_range = np.linspace(0, 10, 1000)
pdf_U = gamma.pdf(u_range, a=2, scale=1/lambda_value)
# グラフのプロット
plt.figure(figsize=(8, 6))
# X1 (X2) の指数分布の描画
plt.plot(x_range, pdf_X1_X2, label='X1 (X2) (指数分布)', color='blue', linestyle='--')
# U のガンマ分布の描画
plt.plot(u_range, pdf_U, label='U = X1 + X2 (ガンマ分布)', color='red')
# グラフの装飾
plt.title('X1 (X2) と U の確率密度関数の比較')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.show()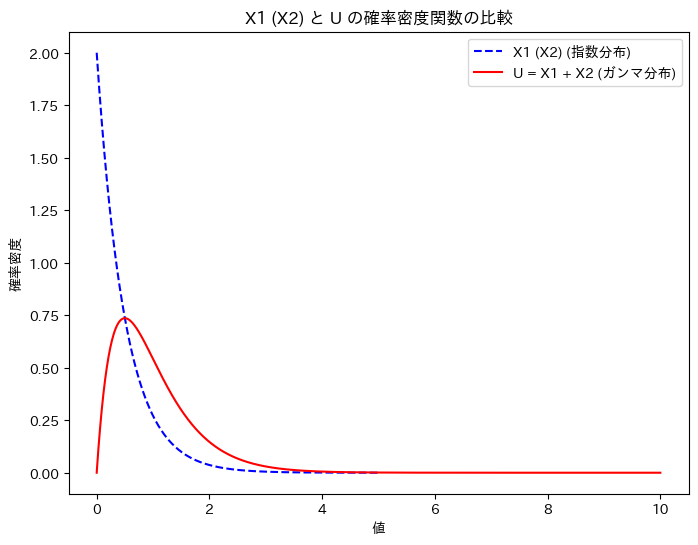
グラフの形状から、U = X1 + X2の関係は想像しづらいですね。
ガンマ分布の形状パラメータを1~2に変化させて、X1 (X2)からUへの変化を確認します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # λ=2
x_range = np.linspace(0, 5, 1000) # X1, X2, U の範囲を0~5に設定
# ガンマ分布の形状パラメータを1から2まで0.1ずつ変化させる
shape_params = np.arange(1, 2.1, 0.1) # 1から2までの形状パラメータを0.1ステップで変化
# グラフのプロット
plt.figure(figsize=(8, 6))
# 形状パラメータが1から2に変化するガンマ分布の描画
for k in shape_params:
gamma_pdf = gamma.pdf(x_range, a=k, scale=1/lambda_value)
plt.plot(x_range, gamma_pdf, label=f'形状パラメータ k={k:.1f}')
# X1 (X2) の指数分布の描画 - 同じなので1つにまとめる
pdf_X1_X2 = lambda_value * np.exp(-lambda_value * x_range)
plt.plot(x_range, pdf_X1_X2, label='X1 (X2) (指数分布)', color='blue', linestyle='--')
# グラフの装飾
plt.title('指数分布からガンマ分布への変化 (形状パラメータの0.1ステップ変化)')
plt.xlabel('値')
plt.ylabel('確率密度')
plt.legend()
# グラフの表示
plt.show()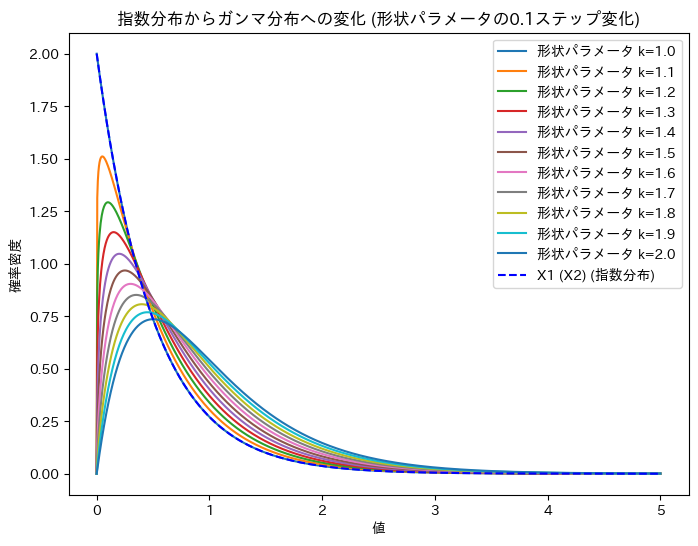
X1 (X2)からUへの変化が可視化できました。
次に、X1 (X2)と、Uの累積分布関数を重ねて描画してみます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon, gamma
# パラメータ設定
lambda_value = 2 # λ=2
x_range = np.linspace(0, 5, 1000) # X1, X2 の範囲
# X1, X2 の指数分布の累積分布関数 (CDF) - 同じなので1つにまとめる
cdf_X1_X2 = expon.cdf(x_range, scale=1/lambda_value)
# U = X1 + X2 は形状パラメータk=2、スケールパラメータθ=1/λのガンマ分布
u_range = np.linspace(0, 10, 1000)
cdf_U = gamma.cdf(u_range, a=2, scale=1/lambda_value)
# グラフのプロット
plt.figure(figsize=(8, 6))
# X1 (X2) の指数分布のCDFの描画
plt.plot(x_range, cdf_X1_X2, label='X1 (X2) (指数分布 CDF)', color='blue', linestyle='--')
# U のガンマ分布のCDFの描画
plt.plot(u_range, cdf_U, label='U = X1 + X2 (ガンマ分布 CDF)', color='red')
# グラフの装飾
plt.title('X1 (X2) と U の累積分布関数 (CDF) の比較')
plt.xlabel('値')
plt.ylabel('累積確率')
plt.legend()
# グラフの表示
plt.show()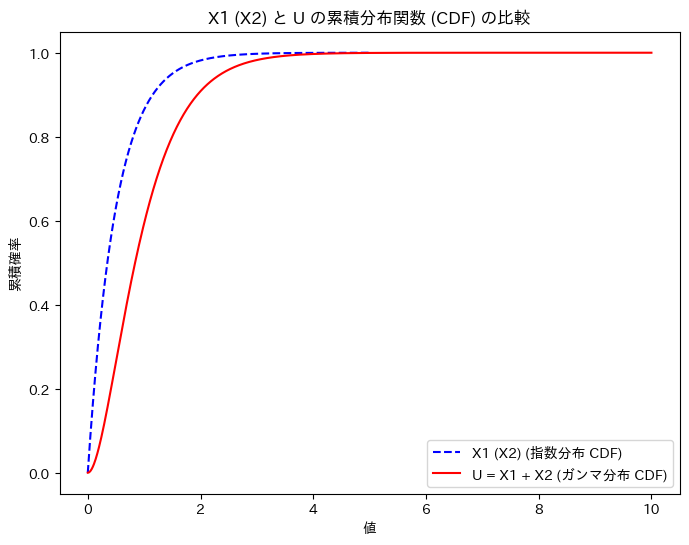
グラフの形状から、U = X1 + X2の関係を想像しやすくなりました。
2019 Q2(1)
独立な指数分布に従う2変数の和の期待値を求めました。
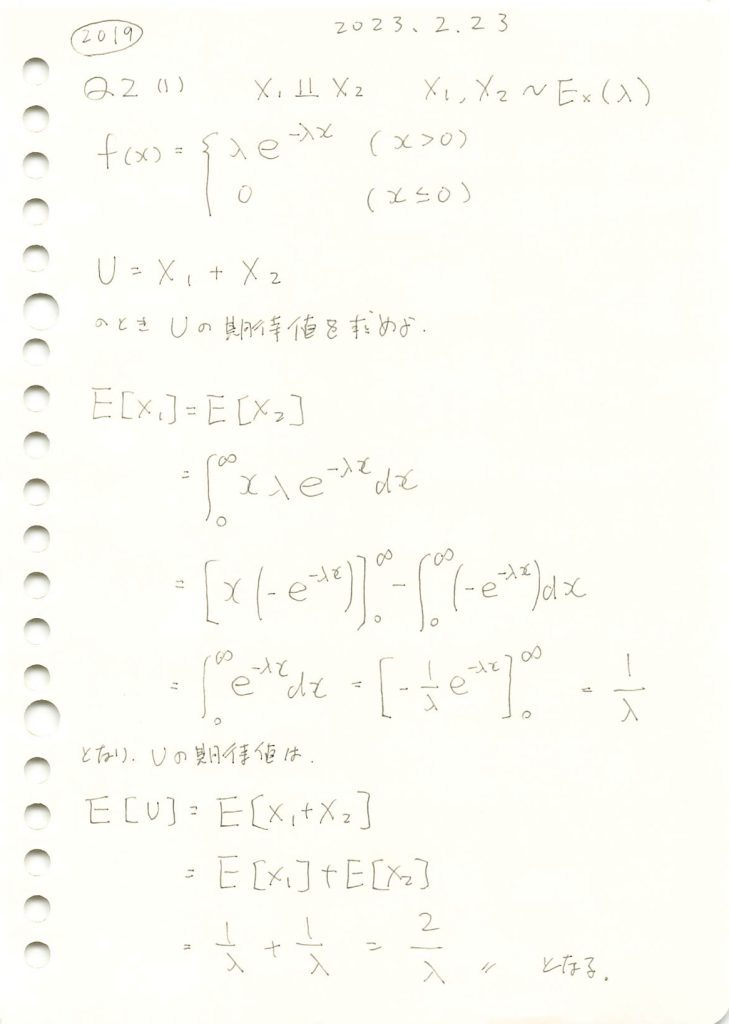
コード
数式を使ってUの期待値を求めます
import sympy as sp
# 変数の定義
x = sp.Symbol('x', positive=True)
lambda_value = sp.Symbol('lambda', positive=True)
# 指数分布の確率密度関数 (PDF)
f_x = lambda_value * sp.exp(-lambda_value * x)
# 期待値の式を計算 (積分)
E_X1 = sp.integrate(x * f_x, (x, 0, sp.oo))
# 期待値
E_X1_simplified = sp.simplify(E_X1)
# X1 + X2 の場合 (独立性より)
E_U = 2 * E_X1_simplified
# 結果の表示
display(E_U)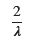
手計算と一致します
次にUに従う乱数を生成し分布を確認します。また形状パラメータ2のガンマ分布と重ねて描画します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma
# パラメータ設定
lambda_value = 2 # 例としてλ=2
num_samples = 1000 # サンプルの数
# 指数分布に従う乱数の生成
X1 = np.random.exponential(scale=1/lambda_value, size=num_samples)
X2 = np.random.exponential(scale=1/lambda_value, size=num_samples)
# U = X1 + X2 の計算
U = X1 + X2
# 理論的な期待値
expected_value = 2 / lambda_value
# シミュレーション結果のヒストグラムのプロット (確率密度にスケール)
plt.hist(U, bins=30, density=True, alpha=0.7, label='シミュレーション結果')
# ガンマ分布 (形状パラメータ k=2, スケールパラメータ θ=1/λ) の確率密度関数 (PDF) を計算
k = 2 # 形状パラメータ (k = 2)
theta = 1 / lambda_value # スケールパラメータ (θ = 1/λ)
# ガンマ分布に基づくx軸の範囲
x = np.linspace(0, max(U), 1000)
# ガンマ分布の確率密度関数 (PDF) を計算
gamma_pdf = gamma.pdf(x, a=k, scale=theta)
# ガンマ分布の折れ線グラフをプロット
plt.plot(x, gamma_pdf, 'r-', label=f'ガンマ分布 (k={k}, θ={theta:.2f})')
# グラフの装飾
plt.axvline(expected_value, color='g', linestyle='--', label=f'理論値 = {expected_value:.2f}')
plt.xlabel('U = X1 + X2')
plt.ylabel('確率密度')
plt.title('Uの分布とガンマ分布の比較')
plt.legend()
plt.show()
# 実際のサンプル平均値と理論的期待値の比較
print(f'理論的な期待値: {expected_value}')
print(f'シミュレーションからの平均値: {np.mean(U)}')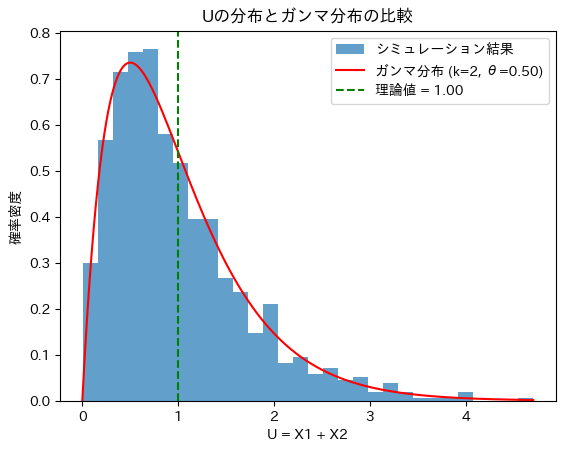
理論的な期待値: 1.0
シミュレーションからの平均値: 0.9902440726761544Uの分布と形状パラメータ2のガンマ分布は重なりました。Uはガンマ分布に従うことが分かります。
2019 Q1(4)
二項分布に従う確率変数Xの不等式が成り立つことの証明をやりました。
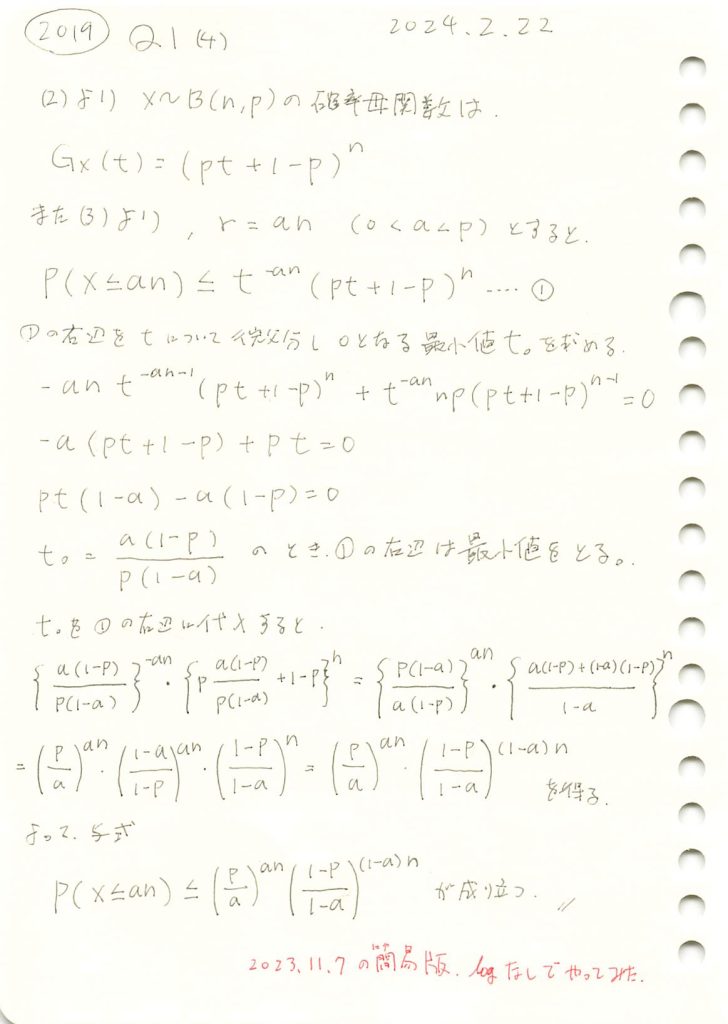
コード
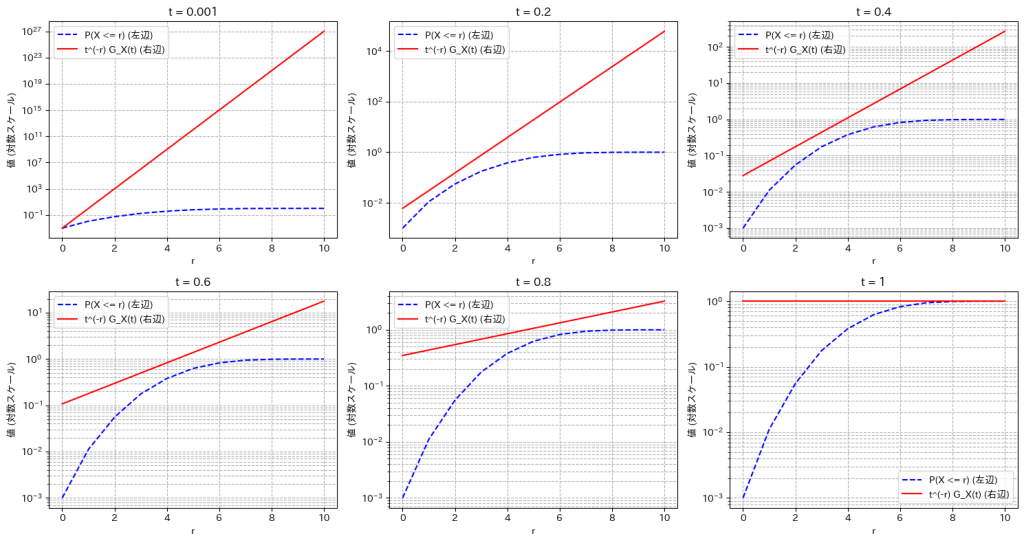
Xが二項分布B(n,p)に従うとき、不等式![]() が成り立つのか可視化して確認しました。
が成り立つのか可視化して確認しました。
# 2019 Q1(4) 2024.9.12
import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt
# パラメータ設定
n_values = [10, 30, 50] # 試行回数 n のリスト
p_values = [0.3, 0.5, 0.7] # 成功確率 p のリスト
a_values = np.linspace(0.01, 0.99, 50) # a の範囲
# サブプロットの作成
fig, axes = plt.subplots(3, 3, figsize=(15, 15)) # 3x3のグリッドでグラフを描画
# グラフの描画ループ
for i, n in enumerate(n_values):
for j, p in enumerate(p_values):
# 左辺と右辺の値を格納するリスト
left_side_values = []
right_side_values = []
for a in a_values:
# 左辺:P(X <= an) の計算
k = int(np.floor(a * n))
left_side = binom.cdf(k, n, p)
left_side_values.append(left_side)
# 右辺の計算
right_side = (p / a) ** (a * n) * ((1 - p) / (1 - a)) ** ((1 - a) * n)
right_side_values.append(right_side)
# グラフの描画(対数スケール)
ax = axes[i, j]
ax.plot(a_values, left_side_values, label='左辺 $P(X \leq an)$', color='blue')
ax.plot(a_values, right_side_values, label='右辺', color='red', linestyle='--')
# 0 < a < p の範囲に色を塗る
ax.axvspan(0, p, color='yellow', alpha=0.3, label="0<a<pの範囲")
ax.set_title(f'n={n}, p={p}')
ax.set_xlabel('$a$')
ax.set_ylabel('値 (対数スケール)')
ax.set_yscale('log') # 縦軸を対数スケールに設定
ax.legend()
ax.grid(True, which="both", ls="--") # 対数スケールのグリッド
# サブプロット間のレイアウト調整
plt.tight_layout()
plt.show()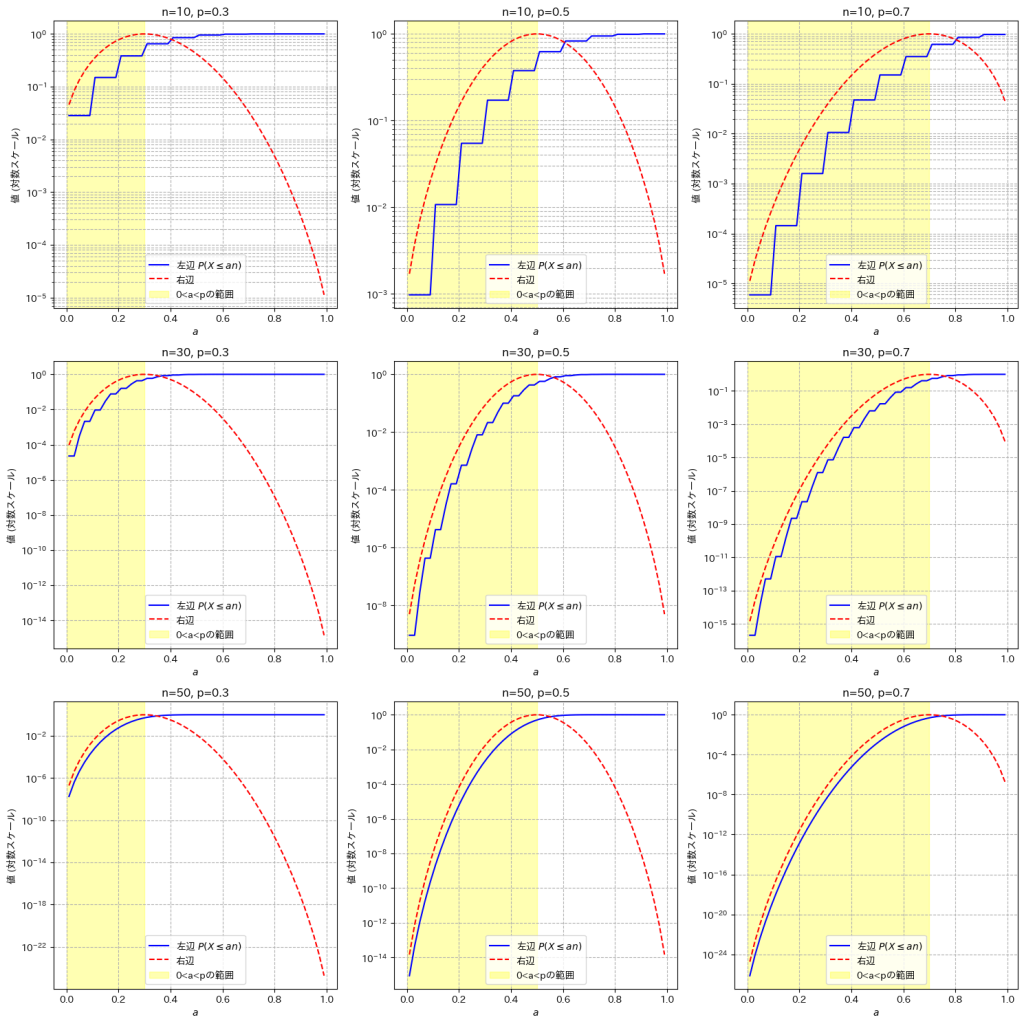
不等式![]() は0<a<pの範囲で成り立っていることが確認できました
は0<a<pの範囲で成り立っていることが確認できました
2021 Q3(1)
ポアソン分布のモーメント母関数を求めました。
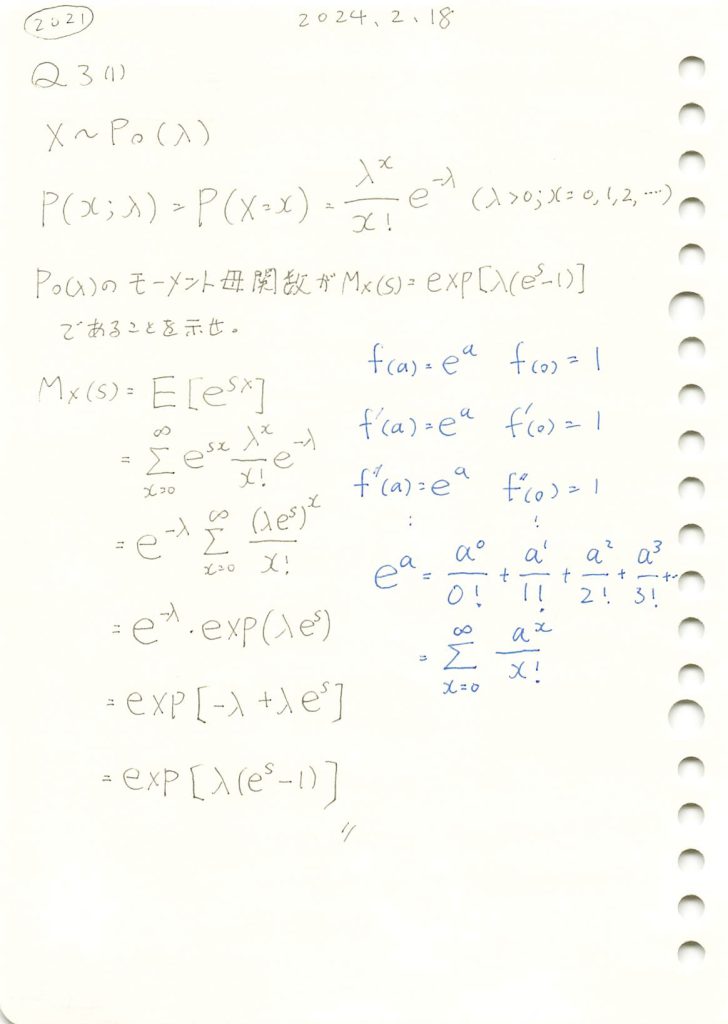
コード
数式を使った計算
# 2021 Q3(1) 2024.8.25
import sympy as sp
# 変数の定義
s, x, lambda_ = sp.symbols('s x lambda_', real=True, positive=True)
# ポアソン分布の確率質量関数 (PMF)
poisson_pmf = (lambda_**x * sp.exp(-lambda_)) / sp.factorial(x)
# モーメント母関数 M_X(s) の定義
M_X = sp.summation(sp.exp(s*x) * poisson_pmf, (x, 0, sp.oo))
# 結果を簡略化
M_X_simplified = sp.simplify(M_X)
# 結果を表示
M_X_simplified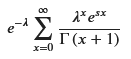
無限級数がe^xの形に変換されないようです。
exp(s) を t に置き換えて、最後に戻してみます。
# 2021 Q3(1) 2024.8.25
import sympy as sp
# 変数の定義
s, x, lambda_, t = sp.symbols('s x lambda_ t', real=True, positive=True)
# exp(s) を t に置き換え
summand = (lambda_ * t)**x / sp.factorial(x)
# モーメント母関数 M_X(s) の定義
M_X = sp.exp(-lambda_) * sp.summation(summand, (x, 0, sp.oo))
# 簡略化
M_X_simplified = sp.simplify(M_X)
# 最後に t を exp(s) に戻す
M_X_final = M_X_simplified.subs(t, sp.exp(s))
# 結果を表示
M_X_final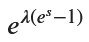
手計算と同じ形になりました。
モーメント母関数を使って期待値と分散を求めます。
import sympy as sp
# 変数の定義
s, lambda_ = sp.symbols('s lambda_', real=True, positive=True)
# モーメント母関数 M_X(s) の定義
M_X = sp.exp(lambda_ * (sp.exp(s) - 1))
# 1次モーメント(期待値)の計算
M_X_prime = sp.diff(M_X, s)
expectation = M_X_prime.subs(s, 0)
# 2次モーメントの計算
M_X_double_prime = sp.diff(M_X_prime, s)
second_moment = M_X_double_prime.subs(s, 0)
# 分散の計算
variance = second_moment - expectation**2
# 結果を表示
display(expectation, variance)
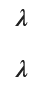
2021 Q2(4)
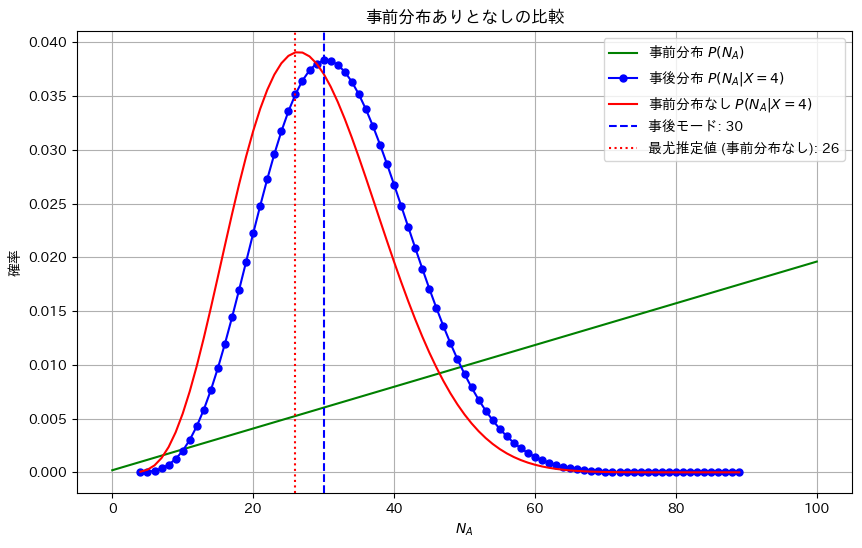
事前分布と尤度から事後確率が最大となるパラメータの推定値を求めました。

コード
数式を使った計算
# 2021 Q2(4) 2024.8.24
import numpy as np
from scipy.special import comb
# 事前分布 P(N_A)
def prior(NA):
return NA + 1
# 尤度関数 P(X = 4 | N_A)
def likelihood(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# 事後分布 P(N_A | X = 4) (正規化定数は省略)
def posterior(NA):
return prior(NA) * likelihood(NA)
# N_A の範囲
NA_values = np.arange(4, 90)
# 事後分布の計算
posterior_values = [posterior(NA) for NA in NA_values]
# 最大値を取る N_A (事後モード) を探索
NA_mode = NA_values[np.argmax(posterior_values)]
NA_mode30プロット
# 2021 Q2(4) 2024.8.24
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import comb
# 事前分布 P(N_A)
def prior(NA):
return NA + 1
# 正規化定数
C = 1 / 5151
# 尤度関数 P(X = 4 | N_A)
def likelihood(NA):
return comb(NA, 4) * comb(100 - NA, 11) / comb(100, 15)
# 事後分布 P(N_A | X = 4)
def posterior(NA):
return prior(NA) * likelihood(NA)
# N_A の範囲を0から100まで(事前分布用)
NA_values_full = np.arange(0, 101)
# 事前分布を計算(0から100まで)
prior_values_full = [C * prior(NA) for NA in NA_values_full]
# N_A の範囲を4から89まで(事後分布用)
NA_values = np.arange(4, 90)
# 事後分布の計算
posterior_values = [posterior(NA) for NA in NA_values]
# 事後分布の正規化
posterior_sum = sum(posterior_values)
posterior_values_normalized = [value / posterior_sum for value in posterior_values]
# 事前分布が存在しない場合の事後分布(尤度のみを正規化)
likelihood_values = [likelihood(NA) for NA in NA_values]
likelihood_sum = sum(likelihood_values)
likelihood_values_normalized = [value / likelihood_sum for value in likelihood_values]
# 3つの分布を重ねて表示
plt.figure(figsize=(10, 6))
# 事前分布のプロット(0から100まで)
plt.plot(NA_values_full, prior_values_full, 'g-', label=r'事前分布 $P(N_A)$', markersize=5)
# 事後分布のプロット(4から89まで)
plt.plot(NA_values, posterior_values_normalized, 'bo-', label=r'事後分布 $P(N_A | X = 4)$', markersize=5)
# 事前分布が存在しない場合の事後分布(尤度のみ)
plt.plot(NA_values, likelihood_values_normalized, 'r-', label=r'事前分布なし $P(N_A | X = 4)$', markersize=5)
# 事後モードのプロット
NA_mode = NA_values[np.argmax(posterior_values_normalized)]
plt.axvline(NA_mode, color='blue', linestyle='--', label=f'事後モード: {NA_mode}')
# 事前分布なしの場合の最尤推定値のプロット
NA_mode_likelihood = NA_values[np.argmax(likelihood_values_normalized)]
plt.axvline(NA_mode_likelihood, color='red', linestyle=':', label=f'最尤推定値 (事前分布なし): {NA_mode_likelihood}')
# グラフの設定
plt.xlabel(r'$N_A$')
plt.ylabel(r'確率')
plt.title(r'事前分布ありとなしの比較')
plt.grid(True)
plt.legend()
plt.show()