標準正規分布に従う確率変数を条件に二値化する確率変数の平均と分散を求めました。
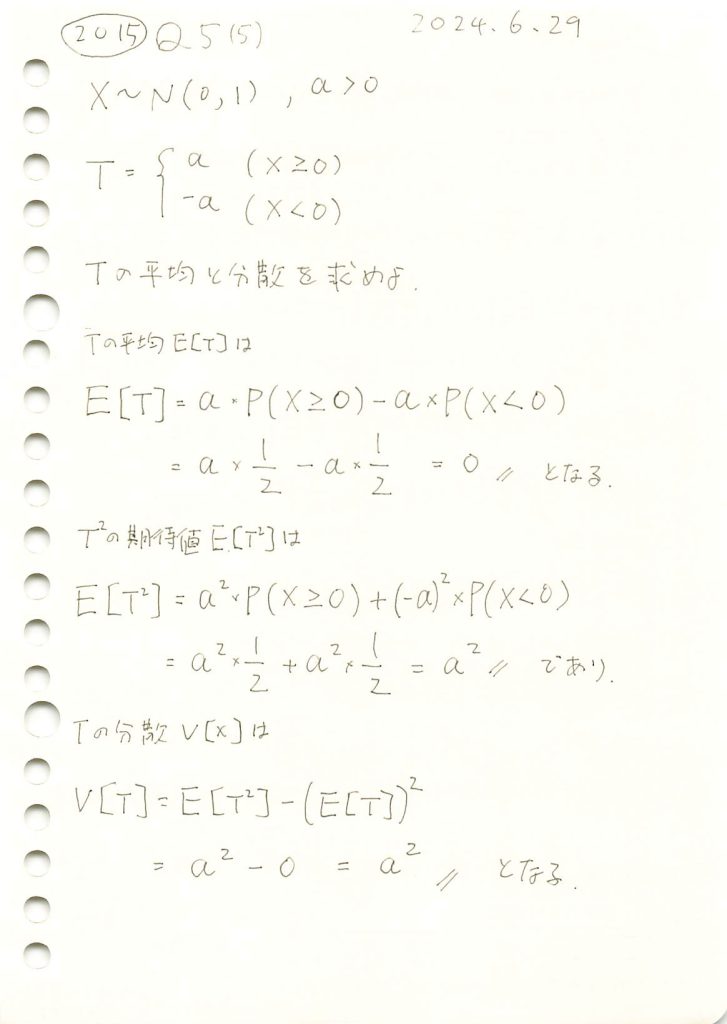
コード
Tの平均と分散をシミュレーションで計算し、それらが理論値と一致するか確認をします。
# 2015 Q5(5) 2024.12.26
import numpy as np
# パラメータ
a = 2 # a の値
num_samples = 100000 # サンプル数
# 正規分布から X を生成
X = np.random.normal(0, 1, num_samples)
# T を定義
T = np.where(X >= 0, a, -a)
# 平均と分散を計算
T_mean = np.mean(T)
T_variance = np.var(T)
# 結果を出力
print("シミュレーション結果:")
print("T の平均 (E[T]):", T_mean)
print("T の分散 (Var(T)):", T_variance)
# 理論値
print("\n理論値:")
print("T の平均 (E[T]):", 0)
print("T の分散 (Var(T)):", a**2)シミュレーション結果:
T の平均 (E[T]): 0.00388
T の分散 (Var(T)): 3.999984945600001
理論値:
T の平均 (E[T]): 0
T の分散 (Var(T)): 4シミュレーションで計算したTの平均と分散は理論値と一致しました。