2つに分けられた標本それぞれの平均と不偏分散を用い、元の平均と不偏分散を式で表しました。

コード
直接アプローチと間接アプローチで求めた![]() と
と![]() が一致するか確認をします。
が一致するか確認をします。
# 2015 Q5(1) 2024.12.22
import numpy as np
import matplotlib.pyplot as plt
# シミュレーションパラメータ
n1 = 30 # グループ1のサンプル数
n2 = 20 # グループ2のサンプル数
n = n1 + n2 # 全体のサンプル数
simulations = 10000 # シミュレーションの回数
# 結果を格納するリスト
y_split = [] # 分割アプローチで計算した平均
y_direct = [] # 直接アプローチで計算した平均
s2_split = [] # 分割アプローチで計算した分散
s2_direct = [] # 直接アプローチで計算した分散
for _ in range(simulations):
# ランダムサンプル生成 (正規分布 N(0, 1) を仮定)
group1 = np.random.normal(0, 1, n1)
group2 = np.random.normal(0, 1, n2)
# グループごとの平均と分散
y1_bar = np.mean(group1)
y2_bar = np.mean(group2)
s1_sq = np.var(group1, ddof=1) # 分散 (不偏推定)
s2_sq = np.var(group2, ddof=1)
# 分割アプローチの平均と分散
y_bar_split = (n1 * y1_bar + n2 * y2_bar) / n
s_sq_split = (
((n1 - 1) * s1_sq + (n2 - 1) * s2_sq) / (n - 1)
+ (n1 * n2 / n) * (y1_bar - y2_bar) ** 2 / (n - 1)
)
# 直接アプローチの平均と分散
all_data = np.concatenate([group1, group2])
y_bar_direct = np.mean(all_data)
s_sq_direct = np.var(all_data, ddof=1)
# データを格納
y_split.append(y_bar_split)
y_direct.append(y_bar_direct)
s2_split.append(s_sq_split)
s2_direct.append(s_sq_direct)
# グラフの描画
fig, axes = plt.subplots(1, 2, figsize=(16, 8))
# 平均の比較
axes[0].scatter(y_split, y_direct, alpha=0.5, color='blue', label=r"分割アプローチ: $\bar{y} = \frac{1}{n}(n_1\bar{y}_1 + n_2\bar{y}_2)$")
axes[0].plot([min(y_split), max(y_split)], [min(y_split), max(y_split)], color='red', linestyle='--', label=r"直接アプローチ: $\bar{y} = \frac{1}{n} \sum_{i=1}^n y_i$")
axes[0].set_xlabel('分割アプローチ (平均)', fontsize=12)
axes[0].set_ylabel('直接アプローチ (平均)', fontsize=12)
axes[0].set_title('平均の比較: 分割 vs 直接', fontsize=14)
axes[0].legend()
axes[0].grid(True)
# 分散の比較
axes[1].scatter(s2_split, s2_direct, alpha=0.5, color='green', label=r"分割アプローチ: $s^2 = \frac{1}{n-1} \left\{(n_1-1)s_1^2 + (n_2-1)s_2^2 + \frac{n_1n_2}{n}(\bar{y}_1 - \bar{y}_2)^2 \right\}$")
axes[1].plot([min(s2_split), max(s2_split)], [min(s2_split), max(s2_split)], color='red', linestyle='--', label=r"直接アプローチ: $s^2 = \frac{1}{n-1}\sum_{i=1}^n (y_i - \bar{y})^2$")
axes[1].set_xlabel('分割アプローチ (分散)', fontsize=12)
axes[1].set_ylabel('直接アプローチ (分散)', fontsize=12)
axes[1].set_title('分散の比較: 分割 vs 直接', fontsize=14)
axes[1].legend()
axes[1].grid(True)
# グラフの表示
plt.tight_layout()
plt.show()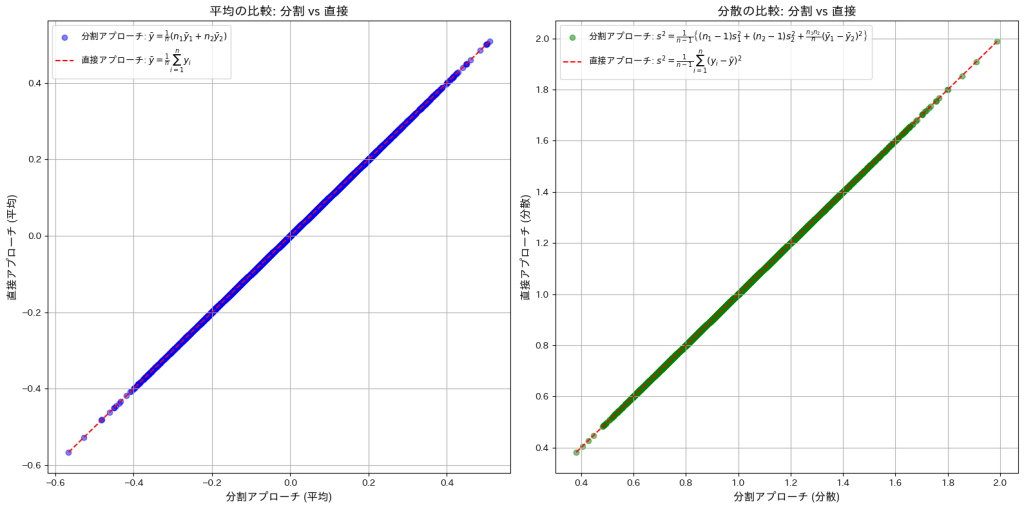
直接アプローチと間接アプローチで求めた![]() と
と![]() が一致しました。
が一致しました。