確率行列が対称行列であるとき、ある新しいパラメータ行列も対称であるか示し、更にその逆が成り立つかも調べました。

コード
セル確率![]() の対称性が成り立つ場合にパラメータ
の対称性が成り立つ場合にパラメータ![]() が対称性
が対称性![]() を持つことを確認します。
を持つことを確認します。
# 2015 Q4(5) 2024.12.21
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# 1. データ生成
np.random.seed(42) # 再現性のためのシード値
I = 4 # 行列のサイズ
p_matrix_sym = np.random.rand(I, I) # 対称性を持たないランダムな確率行列
p_matrix_sym = (p_matrix_sym + p_matrix_sym.T) / 2 # 対称性を強制
# 対称性が成り立たない確率行列
p_matrix_asym = np.random.rand(I, I)
p_matrix_asym = p_matrix_asym / np.sum(p_matrix_asym) # 正規化
# 正規化して確率にする
p_matrix_sym = p_matrix_sym / np.sum(p_matrix_sym)
# 2. λ_ij の計算関数
def calculate_lambda(p_matrix):
I = p_matrix.shape[0]
lambdas = np.zeros((I, I))
for i in range(1, I):
for j in range(1, I):
lambdas[i, j] = np.log(p_matrix[i, j] * p_matrix[0, 0] / (p_matrix[i, 0] * p_matrix[0, j]))
return lambdas
# 対称性の仮説が成り立つ場合の λ_ij
lambda_sym = calculate_lambda(p_matrix_sym)
# 対称性の仮説が成り立たない場合の λ_ij
lambda_asym = calculate_lambda(p_matrix_asym)
# 3. 可視化: ヒートマップをプロット
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
# 対称性が成り立つ確率行列
sns.heatmap(p_matrix_sym, annot=True, fmt=".3f", cmap="Blues", ax=axes[0, 0])
axes[0, 0].set_title("対称性が成り立つ確率行列 $p_{ij}$")
# 対称性が成り立つ λ_ij 行列
sns.heatmap(lambda_sym, annot=True, fmt=".3f", cmap="Greens", ax=axes[0, 1])
axes[0, 1].set_title("対称性が成り立つ場合の $\lambda_{ij}$")
# 対称性が成り立たない確率行列
sns.heatmap(p_matrix_asym, annot=True, fmt=".3f", cmap="Reds", ax=axes[1, 0])
axes[1, 0].set_title("対称性が成り立たない確率行列 $p_{ij}$")
# 対称性が成り立たない λ_ij 行列
sns.heatmap(lambda_asym, annot=True, fmt=".3f", cmap="Purples", ax=axes[1, 1])
axes[1, 1].set_title("対称性が成り立たない場合の $\lambda_{ij}$")
plt.tight_layout()
plt.show()
# 4. λ_ij = λ_ji の確認
print("対称性が成り立つ場合:")
print("λ_ij == λ_ji:", np.allclose(lambda_sym, lambda_sym.T))
print("\n対称性が成り立たない場合:")
print("λ_ij == λ_ji:", np.allclose(lambda_asym, lambda_asym.T))
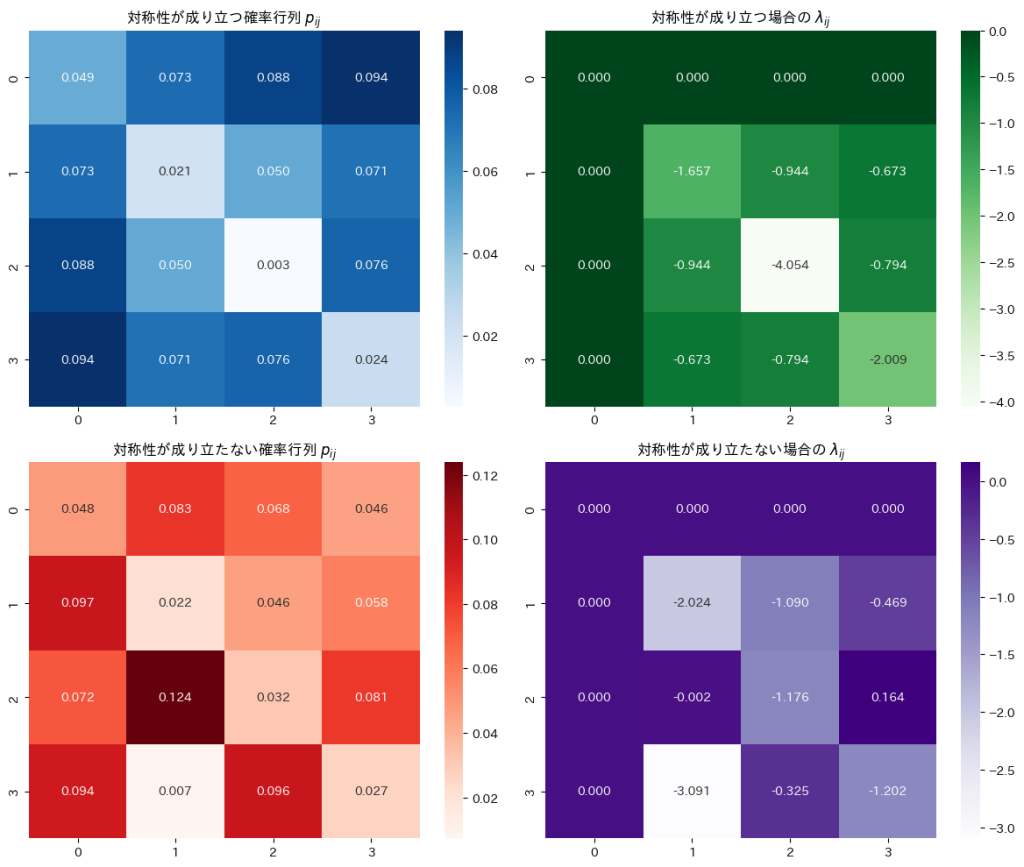
セル確率![]() の対称性が成り立つ場合に、パラメータ
の対称性が成り立つ場合に、パラメータ![]() が対称性
が対称性![]() を持つことを確認しました。
を持つことを確認しました。