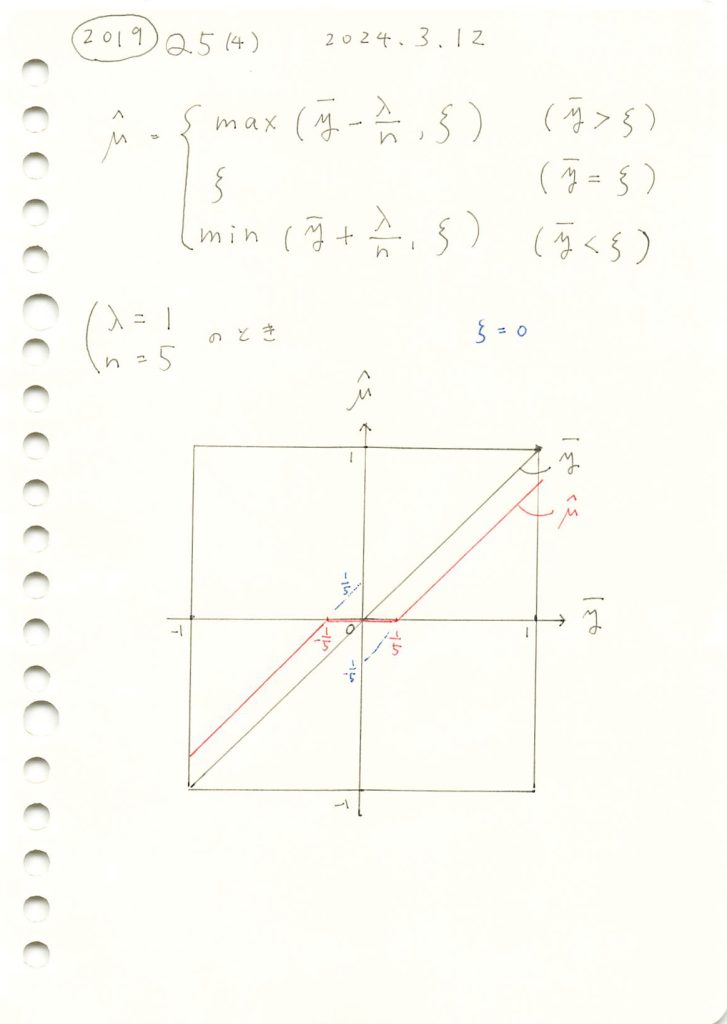
前問の式をグラフに描画しました。
コード
グラフをプロットします。
# 2019 Q5(4) 2024.9.30
import numpy as np
import matplotlib.pyplot as plt
# μハット(事後分布のモード)を計算する関数
def mu_hat(y_mean, lambd, xi, n):
if y_mean > xi:
return max(y_mean - lambd / n, xi)
elif y_mean < xi:
return min(y_mean + lambd / n, xi)
else:
return xi
# パラメータ設定
xi = 0 # ラプラス分布の中央値
lambd = 1 # スケールパラメータ
n_samples = 5 # サンプル数
# ȳ(観測データの平均)の範囲を設定 (-1 から 1)
y_mean_values = np.linspace(-1, 1, 500)
# μハットの値を計算
mu_hat_values = [mu_hat(y_mean, lambd, xi, n_samples) for y_mean in y_mean_values]
# グラフをプロット
plt.plot(y_mean_values, mu_hat_values, label='μハット (事後分布のモード)', color='red')
plt.plot(y_mean_values, y_mean_values, label='ȳ (標本平均)', color='blue', linestyle='--')
plt.title(f'標本平均 ȳ と 推定値 μハットの比較 (ξ = {xi}, λ = {lambd}, n = {n_samples})')
plt.xlabel('ȳ (標本平均)')
plt.ylabel('μハット (推定値)')
plt.legend()
plt.grid(True)
plt.show()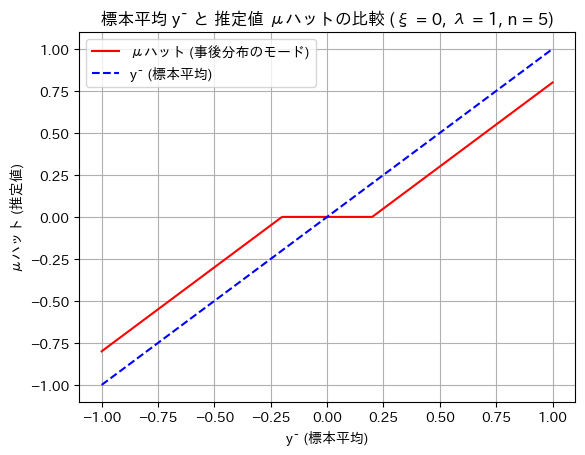
![]() がξに近いとき、
がξに近いとき、![]() はξになるという特徴があるようです。
はξになるという特徴があるようです。