前問の事後確率密度関数の最大値を取る期待値μを求めました。

追記
■2025/2/4 ![]() や
や![]() の導き方
の導き方
![]()
を変形し
![]()
となる。
ここで、![]() と
と![]() の符号を考えると、同符号のとき、第一項は異符号のときと比べて大きくなる。なぜなら
の符号を考えると、同符号のとき、第一項は異符号のときと比べて大きくなる。なぜなら
AとBが同符号のときの![]() のほうが
のほうが
AとBが異符号のときの![]() よりも大きいからだ。
よりも大きいからだ。
一方で第二項![]() は変化しない。よって、
は変化しない。よって、
![]() と、
と、![]() は同符号となるから
は同符号となるから
![]() のときは
のときは![]() と言えるので
と言えるので
![]() は、
は、![]() を下回らないので
を下回らないので
![]() のように書ける。
のように書ける。
同様に
![]() のときは
のときは![]() と言えるので
と言えるので
![]() は、
は、![]() を上回らないので
を上回らないので
![]() のように書ける。
のように書ける。
まとめると
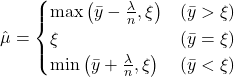
となる。
コード
対数事後分布 h(μ)と、その第1項(観測データに基づく項)および第2項(事前分布に基づく項)のグラフを描画します。パラメータ ξ を 1 または 5、スケールパラメータ λ を 25 または 50 として、それぞれの組み合わせで描画します。
# 2019 Q5(3) 2024.9.29
import numpy as np
import matplotlib.pyplot as plt
# 対数事後分布の第1項: 観測データに基づく項
def h_term1(mu, y):
n = len(y)
y_mean = np.mean(y)
return -0.5 * n * (mu - y_mean)**2
# 対数事後分布の第2項: 事前分布に基づく項
def h_term2(mu, lambd, xi):
return -lambd * np.abs(mu - xi)
# 対数事後分布 h(μ) の定義
def h(mu, y, lambd, xi):
return h_term1(mu, y) + h_term2(mu, lambd, xi)
# μハット(事後分布のモード)を計算
def mu_hat(y_mean, lambd, xi, n):
if y_mean > xi:
return max(y_mean - lambd / n, xi)
elif y_mean < xi:
return min(y_mean + lambd / n, xi)
else:
return xi
# パラメータ設定のリスト (xi, lambd) の組み合わせ
params = [(1, 25), (1, 50), (5, 25), (5, 50)]
n_samples = 20 # サンプル数
mu_values = np.linspace(0, 6, 500) # μの範囲
# グラフを4つ表示するための設定
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
for i, (xi, lambd) in enumerate(params):
# 観測データを生成して、平均を3に調整
np.random.seed(43)
y = np.random.normal(loc=3, scale=1, size=n_samples)
y_mean = np.mean(y)
# μハットを計算
mu_hat_value = mu_hat(y_mean, lambd, xi, n_samples)
# 各項の計算
h_values = h(mu_values, y, lambd, xi)
h_term1_values = h_term1(mu_values, y)
h_term2_values = h_term2(mu_values, lambd, xi)
# サブプロットに描画
ax = axes[i//2, i%2]
ax.plot(mu_values, h_values, label='h(μ)', color='orange')
ax.plot(mu_values, h_term1_values, label='第1項: -n/2 (μ - ȳ)²', color='blue')
ax.plot(mu_values, h_term2_values, label='第2項: -λ|μ - ξ|', color='green')
# μハットを縦線でプロット
ax.axvline(mu_hat_value, color='red', linestyle='--', label=f'μハット = {mu_hat_value:.2f}')
# グラフのタイトル
ax.set_title(f'ξ = {xi}, λ = {lambd}, ȳ = {y_mean:.2f}, n = {n_samples}')
ax.set_xlabel('μ')
ax.set_ylabel('値')
ax.legend()
ax.grid(True)
# グラフを描画
plt.tight_layout()
plt.show()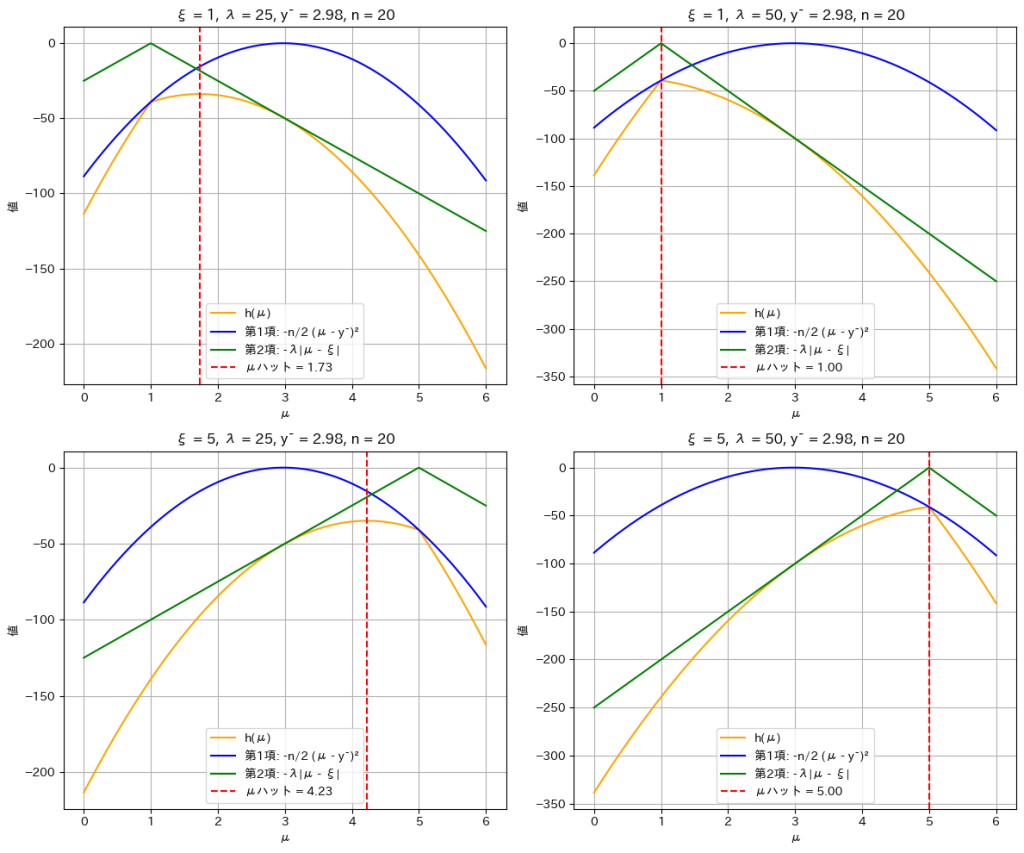
対数事後分布 h(μ)が最大値を取るμハットが
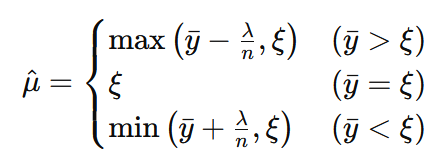
であることが確認できました。