ラプラス分布に従う確率変数μを母平均とする正規分布の観測値からμの事後確率密度関数を求めました。

コード
数式を使って事後確率密度関数g(μ|y)を求めます。
# 2019 Q5(2) 2024.9.28
import sympy as sp
# シンボリック変数の定義
mu, xi, lambd, n = sp.symbols('mu xi lambda n')
y = sp.IndexedBase('y')
i = sp.symbols('i', integer=True)
# ラプラス分布の事前分布
laplace_prior = (lambd / 2) * sp.exp(-lambd * sp.Abs(mu - xi))
# 正規分布の尤度関数
likelihood = (1 / (2 * sp.pi)**(n / 2)) * sp.exp(-sp.Sum((y[i] - mu)**2 / 2, (i, 1, n)))
# 事後分布 (比例定数は無視)
posterior = laplace_prior * likelihood
# 結果を簡略化
posterior_simplified = sp.simplify(posterior)
# 結果を表示
posterior_simplified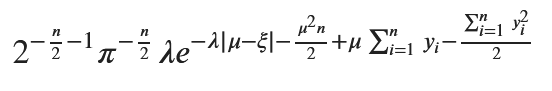
形は少し違いますが手計算の結果と一致しました。
次に、事前分布と事後分布の確率密度関数をプロットします。比較しやすいように事後分布は正規化します。また事前分布がない場合として尤度関数も重ねて描画してみましょう。
# 2019 Q5(2) 2024.9.28
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import simps
# 事前分布(ラプラス分布)の定義
def laplace_prior(mu, xi, lambd):
return (lambd / 2) * np.exp(-lambd * np.abs(mu - xi))
# 事後分布(正規化定数は省略)
def posterior_example(mu, y, xi, lambd):
n = len(y)
y_mean = np.mean(y)
sum_y = np.sum((y - y_mean)**2)
# 解答例の事後分布
return (lambd / (2 * (2 * np.pi)**(n / 2))) * np.exp(-0.5 * (sum_y + n * (mu - y_mean)**2) - lambd * np.abs(mu - xi))
# 尤度関数(事前分布がない場合)
def likelihood(mu, y):
n = len(y)
y_mean = np.mean(y)
return np.exp(-0.5 * n * (mu - y_mean)**2)
# パラメータ設定
xi = 0 # ラプラス分布の中央値
lambd = 1 # スケールパラメータ
n_samples = 20 # サンプル数
# 観測データを生成
np.random.seed(43)
y = np.random.normal(loc=0, scale=1, size=n_samples)
# μの範囲を設定
mu_values = np.linspace(-3, 3, 500)
# 事前分布の計算
prior_values = laplace_prior(mu_values, xi, lambd)
# 事後分布の計算(事前分布あり)
posterior_values_example = posterior_example(mu_values, y, xi, lambd)
# 尤度関数の計算(事前分布なし)
likelihood_values = likelihood(mu_values, y)
# 事後分布と尤度関数を正規化
area_under_curve_example = simps(posterior_values_example, mu_values) # 数値積分
posterior_values_example /= area_under_curve_example # 正規化
area_under_likelihood = simps(likelihood_values, mu_values) # 数値積分
likelihood_values /= area_under_likelihood # 正規化
# グラフをプロット
plt.plot(mu_values, prior_values, label='事前分布 (ラプラス分布)', color='blue')
plt.plot(mu_values, posterior_values_example, label='事後分布', color='purple')
plt.plot(mu_values, likelihood_values, label='尤度関数(事前分布なし)', color='green', linestyle='--')
plt.title('事前分布、事後分布、および事前分布がない場合の尤度関数の比較')
plt.xlabel('μ')
plt.ylabel('確率密度')
plt.legend()
plt.show()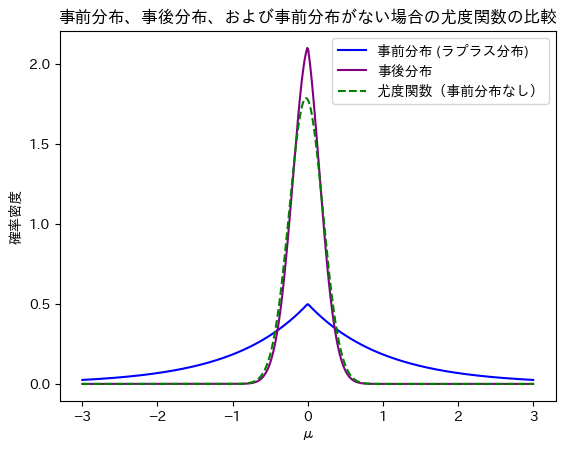
事後分布は事前分布と尤度関数の中間的な形をとっていることが分かります。