ラプラス分布の期待値を求めました。

コード
ξ=0,λ=1のラプラス分布 ![]() の期待値E[μ]と分散V[μ]を求めます。
の期待値E[μ]と分散V[μ]を求めます。
# 2019 Q5(1) 2024.9.27
import numpy as np
import matplotlib.pyplot as plt
# パラメータの設定
xi = 0 # 理論的な期待値
lambda_ = 1 # スケールパラメータ
n_samples = 10000 # サンプル数
# ラプラス分布からランダムサンプルを生成
samples = np.random.laplace(loc=xi, scale=1/lambda_, size=n_samples)
# シミュレーションの期待値と分散を計算
sample_mean = np.mean(samples)
sample_variance = np.var(samples)
# 理論値
theoretical_mean = xi
theoretical_variance = 2 / lambda_**2
# 理論値とシミュレーション値を出力
print(f"シミュレーションによる期待値 E[μ]: {sample_mean}")
print(f"理論的な期待値 E[μ]: {theoretical_mean}")
print(f"シミュレーションによる分散 V[μ]: {sample_variance}")
print(f"理論的な分散 V[μ]: {theoretical_variance}")
# 理論的なラプラス分布のPDFを描画
mu_values = np.linspace(-10, 10, 1000)
pdf_values = (lambda_ / 2) * np.exp(-lambda_ * np.abs(mu_values - xi))
# ヒストグラムの描画
plt.hist(samples, bins=50, density=True, alpha=0.6, color='g', label='シミュレーションデータ')
# 理論的なPDFを線で描画
plt.plot(mu_values, pdf_values, 'r-', lw=2, label='理論的なPDF')
# グラフの設定
plt.title('ラプラス分布:シミュレーション vs 理論的なPDF')
plt.xlabel('値')
plt.ylabel('密度')
plt.legend()
plt.show()シミュレーションによる期待値 E[μ]: -8.093411765355611e-05
理論的な期待値 E[μ]: 0
シミュレーションによる分散 V[μ]: 2.043434597873531
理論的な分散 V[μ]: 2.0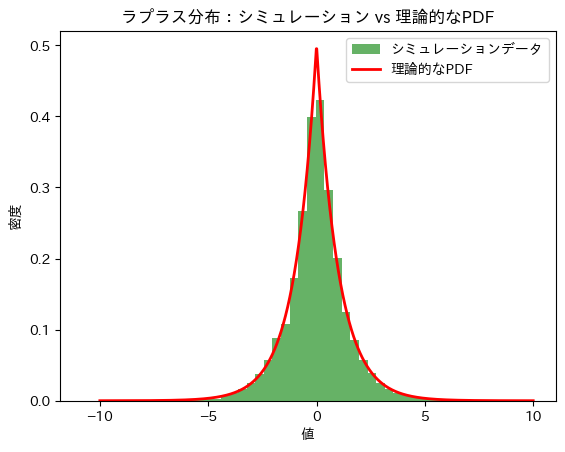
シミュレーションによる期待値E[μ]と分散V[μ]は理論値に近い値をとりました。