コーシー分布の検定での第一種過誤確率を求めました。
コード
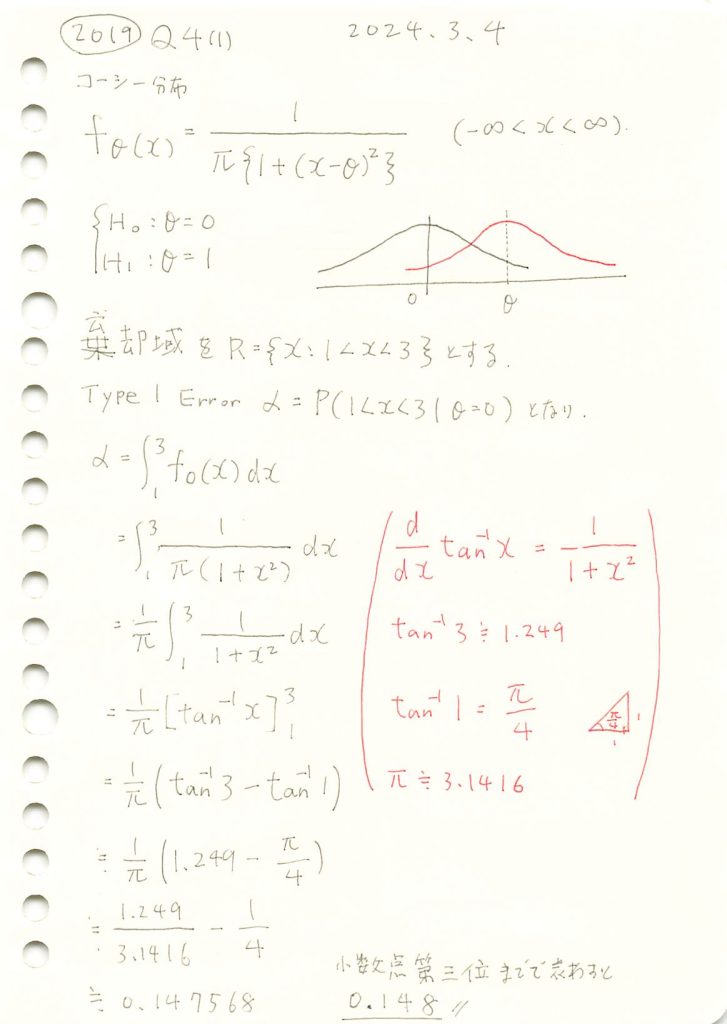
数式を使って第一種の過誤確率αを求めます。
# 2019 Q4(1) 2024.9.23
import numpy as np
from scipy.integrate import quad
# コーシー分布の確率密度関数 (theta = 0)
def cauchy_pdf(x):
return 1 / (np.pi * (1 + x**2))
# 積分範囲(棄却域R = (1, 3))
lower_bound = 1
upper_bound = 3
# 積分を実行
alpha, error = quad(cauchy_pdf, lower_bound, upper_bound)
# 結果を表示(小数第3位まで表示)
print(f"第一種の過誤確率 α: {alpha:.3f}")第一種の過誤確率 α: 0.148手計算と一致しました。
次に、数値シミュレーションで計算をしてみます。なお、コーシー分布は裾が重いため-8 ~8の範囲になるようにフィルターを掛けることにします。
# 2019 Q4(1) 2024.9.23
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import cauchy
# シミュレーションのパラメータ
np.random.seed(43)
num_trials = 100000
# 棄却域 R = (1, 3)
lower_bound = 1
upper_bound = 3
# コーシー分布 (θ = 0) からのサンプルを生成
samples = np.random.standard_cauchy(size=num_trials)
# -8 から 8 の範囲にサンプルを制限して外れ値を除外
filtered_samples = samples[(samples > -8) & (samples < 8)]
# 棄却域に入っているかどうかを判定
reject = (samples > lower_bound) & (samples < upper_bound)
# 棄却域に入った割合が第一種の過誤確率 α
alpha_simulated = np.mean(reject)
# 結果を表示
print(f"シミュレーションによる第一種の過誤確率 α: {alpha_simulated:.3f}")
# ヒストグラムのプロット(フィルタリングしたサンプルを使う)
plt.figure(figsize=(10, 6))
plt.hist(filtered_samples, bins=100, density=True, alpha=0.5, color='blue', label='シミュレーション結果(フィルタリング済み)')
# 理論的なコーシー分布の確率密度関数 (theta = 0) をプロット
x = np.linspace(-8, 8, 1000) # 横のレンジを -8 から 8 に設定
pdf = cauchy.pdf(x)
plt.plot(x, pdf, 'r-', lw=2, label='理論的コーシー分布の確率密度関数')
# 棄却域を塗りつぶす
plt.axvspan(lower_bound, upper_bound, color='red', alpha=0.3, label='棄却域 (1 < x < 3)')
# グラフの設定
plt.xlim(-8, 8) # 横のレンジを -8 から 8 に設定
plt.xlabel('x')
plt.ylabel('密度')
plt.title(f'コーシー分布のシミュレーションと棄却域\nシミュレーションによる α = {alpha_simulated:.3f}')
plt.legend()
plt.grid(True)
# グラフを表示
plt.show()シミュレーションによる第一種の過誤確率 α: 0.148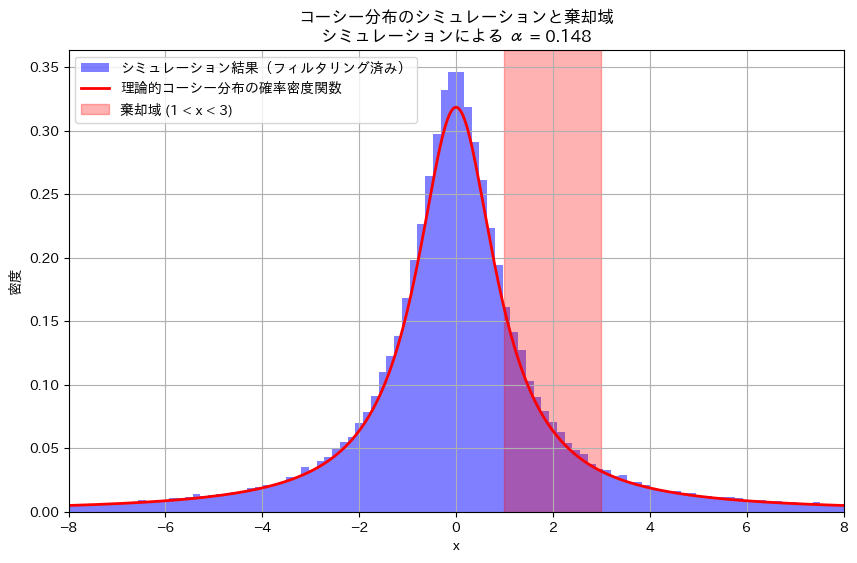
シミュレーション結果も手計算と一致しました。