一様分布に従う複数の確率変数がとる最大値の期待値と、その最大値から上限θの不偏推定量を求めました。
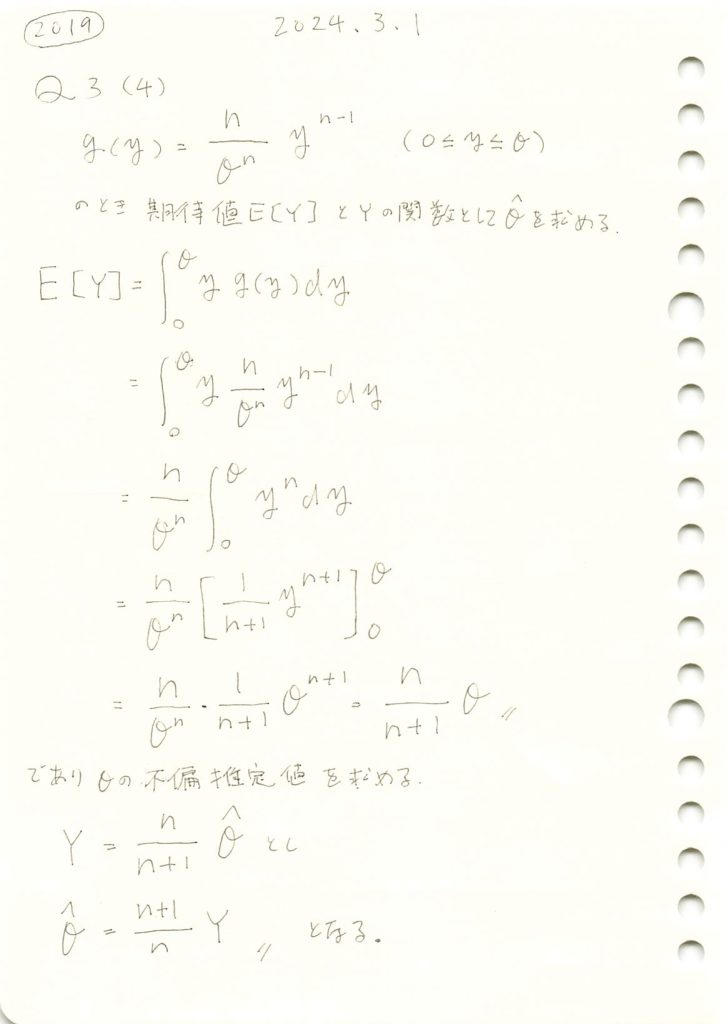
コード
数式を使って期待値E(Y)とθの不偏推定量を求めます。
# 2019 Q3(4) 2024.9.20
import sympy as sp
# シンボリック変数の定義
y, theta, n = sp.symbols('y theta n', positive=True, real=True)
# 最大値Yの確率密度関数 f_Y(y)
f_Y = (n / theta**n) * y**(n-1)
# 期待値 E[Y] の定義
E_Y = sp.integrate(y * f_Y, (y, 0, theta))
# 期待値 E[Y] の表示
print(f"E[Y] の導出結果:")
display(sp.simplify(E_Y))
# 改行を追加
print()
# 新しいシンボリック変数Yの定義
Y = sp.symbols('Y', positive=True, real=True)
# 理論的な E[Y] の式(E[Y] = n/(n+1) * theta)
theoretical_E_Y = (n / (n + 1)) * theta
# Y を基にして theta を求める方程式を解く
theta_hat = sp.solve(Y - theoretical_E_Y, theta)[0]
# 不偏推定量の結果表示
print(f"不偏推定量 θ̂ の導出結果:")
display(theta_hat)
式の形は少し違いますが正しいですね。
次に、数値シミュレーションにより期待値E(Y)とθの不偏推定量求め理論値と比較します。
# 2019 Q3(4) 2024.9.20
import numpy as np
import matplotlib.pyplot as plt
# パラメータ設定
theta_true = 10 # 真のθ
n = 15 # サンプルサイズ
num_simulations = 10000 # シミュレーション回数
# シミュレーションでの最大値Yを格納するリスト
max_values = []
# シミュレーション開始
for _ in range(num_simulations):
# U(0, theta_true) から n 個の乱数を生成
samples = np.random.uniform(0, theta_true, n)
# その中での最大値Yを記録
max_values.append(np.max(samples))
# シミュレーションによる期待値E[Y]を計算
simulated_E_Y = np.mean(max_values)
# 理論値E[Y]を計算
theoretical_E_Y = (n / (n + 1)) * theta_true
# 不偏推定量のシミュレーション
theta_hat_simulated = (n + 1) / n * np.mean(max_values)
# 結果の表示
print(f"シミュレーションによる E[Y]: {simulated_E_Y}")
print(f"理論値 E[Y]: {theoretical_E_Y}")
print(f"シミュレーションによる不偏推定量 θ̂: {theta_hat_simulated}")
print(f"真の θ: {theta_true}")
# ヒストグラムを描画して結果を視覚化
plt.hist(max_values, bins=30, density=True, alpha=0.7, color='blue', edgecolor='black', label='シミュレーション結果')
plt.axvline(simulated_E_Y, color='red', linestyle='--', label=f'シミュレーション E[Y] = {simulated_E_Y:.2f}')
plt.axvline(theoretical_E_Y, color='green', linestyle='--', label=f'理論値 E[Y] = {theoretical_E_Y:.2f}')
# グラフ設定
plt.title('最大値Yの分布とE[Y]')
plt.xlabel('Y の値')
plt.ylabel('密度')
plt.legend()
plt.grid(True)
plt.show()シミュレーションによる E[Y]: 9.384118720046189
理論値 E[Y]: 9.375
シミュレーションによる不偏推定量 θ̂: 10.009726634715935
真の θ: 10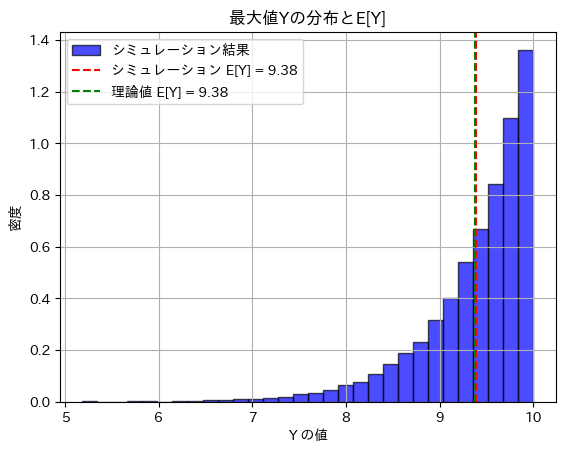
期待値E(Y)とθの不偏推定量は理論値に近い値を取りました。